find the antiderivative of g(x)=−8ex 4−5x 7−5sec2(x 6). (do not include the constant c in your answer.)
Answers
The antiderivative of g(x) is -2e^(4x) - 5/6x^6 + 5tan(x-6) + C.
We can apply integration by parts to the first term, and substitution to the second term:
Let u = -8ex and dv = x^4-5x^7 dx
Then du/dx = -8ex and v = x^5/5 - x^8/8
Applying integration by parts:
∫-8ex(x^4-5x^7)dx = -8ex(x^5/5 - x^8/8) - ∫(-8ex)(5x^4-35x^6)dx
Simplifying the second integral:
∫(-8ex)(5x^4-35x^6)dx = -40ex(x^4-7x^6)/5
Now let u = -5sec^2(x-6) and dv = dx
Then du/dx = -10sec(x-6)tan(x-6) and v = x
Applying substitution:
∫-5sec^2(x-6)dx = -5tan(x-6)
Putting it all together:
∫g(x)dx = -8ex(x^5/5 - x^8/8 + 40x^4/5 - 280x^6/5) - 5tan(x-6) + C
where C is the constant of integration.
To know more about antiderivative,
https://brainly.com/question/31413996
#SPJ11
Related Questions
Part of the population of 7,000 elk at a wildlife preserve is infected with a parasite. A random sample of 50 elk shows that 7 of them are infected. How many elk are likely to be infected?
Answers
Answer:
620
Explanation:
When the sample is given, the number of elk are likely to be infected is to be considered as the 620.
Calculation of the number of elk:
Since the population is 7,750.
The random sample is 50.
So here be like
= 620
hence, When the sample is given, the number of elk are likely to be infected is to be considered as the 620.
A tank of water is in the shape of a right circular cone with height 8 meters and base radius 26 meters. The tank is being filled with water at a rate of 12m3/s. When the radius of the top of the water is 10 meters, how fast is the depth of the water changing
Answers
The depth of the water is changing at a rate of approximately 0.39 m/s when the radius of the top of the water is 10 meters.
To find the rate at which the depth of the water is changing, we can use related rates.
Given:
Height of the cone (h) = 8 meters
Base radius (r) = 26 meters
Rate of filling (dV/dt) = 12 m³/s
Radius of the top of the water (x) = 10 meters
First, we establish the relationship between the height and radius of the cone using similar triangles. The ratio of the height to the radius is constant, so we have h/r = 8/26.
Next, we differentiate both sides of the equation with respect to time (t) to find dh/dt in terms of dx/dt. This gives us (dh/dt)/(dr/dt) = 0.3077.
We can then substitute the given values into the equation: (dh/dt)/(dx/dt) = 0.3077. Rearranging the equation, we find that dx/dt = (dh/dt) / 0.3077.
To find the value of dh/dt, we can substitute the given rate of filling, dV/dt = 12 m³/s, into the equation. Solving for dh/dt, we get dh/dt = 3.693 m/s.
Finally, we substitute the values of dh/dt and 0.3077 into the equation to find dx/dt. This gives us dx/dt ≈ 0.39 m/s.
Therefore, the depth of the water is changing at a rate of approximately 0.39 m/s when the radius of the top of the water is 10 meters.
To know more about Depth visit:
https://brainly.com/question/13804949
#SPJ11
A cylinder has a surface area of about 221.1 square meters and a height of
7.8 meters. What is the approximate radius of the cylinder?
OA. 3.2 meters
OB. 4.5 meters
OC. 2.1 meters
OD. 6.4 meters

Answers
The approximate radius of the cylinder is 4.5m
Surface area of cylinderThe formula for calculating the surface area of cylinder is expressed as:
SA = 2πr(r+h)
where
r is the radius
h is the height
Given the following parameters
SA = 221.1 square meters
height = 7.8m
Substitute
221.1= 2(3.14)r(r+7.8)
221.1 = 6.28r^2 + 15.6r
Factorize to have
6.28r^2 + 15.6r - 221.6 = 0
On factoring, the value of the radius is 4.5 meters
Learn more on surface area of cylinder here: https://brainly.com/question/76387
#SPJ1
Answer:
the answer is A
Step-by-step explanation:
I hope it helps you
make an equation and solve for x, 25 points.
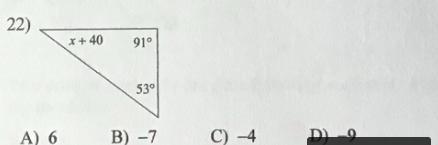
Answers
Answer:
Equation : x + 40° + 91° + 53° = 180°
All angles in a triangle add up to 180°
The value of x is -4.
Now,
x + 40 + 91° + 53° = 180° ( ▼ Sum of three
angle of triangle is 180°)
x + 184 = 180
x = 180 - 184
▲ x = - 4
This is a Right answer....
Mark me as brainliest...
I hope you understand...
A rectangular grazing area is to be fenced off on three sides using part of a 100100 meter rock wall as the fourth side. Fence posts are to be placed every 1212 meters along the fence including the two posts where the fence meets the rock wall. What is the fewest number of posts required to fence an area 3636 m by 6060 m
Answers
The fewest number of posts required to fence an area of 36 meters by 60 meters is 12 posts.
How to find the least number of posts for a rectangular fence
According the information given by the statement, the number of posts (\(n\)) is determined by the following formula:
\(n = 1 + \frac{2\cdot x_{1}+x_{2}}{d} \) (1)
Where:
\(x_{1}, x_{2}\) - Dimensions of the rectangular fence, in meters. \(d\) - Distance between posts, in meters.The fewest number of posts is represented by the minimum \(n\) associated to a combination of \(x_{1}\) and \(x_{2}\).
Test 1 - \(x_{1} = 36\,m\), \(x_{2} = 60\,m\), \(d = 12\,m\)\(n = 1 + \frac{2\cdot (36\,m)+60\,m}{12\,m} \)
\(n = 12\)
Test 2 - \(x_{1} = 60\,m\), \(x_{2} = 36\,m\), \(d = 12\,m\)\(n = 1 + \frac{2\cdot (60\,m)+36\,m}{12\,m} \)
\(n = 14\)
Hence, the fewest number of posts required to fence an area of 36 meters by 60 meters is 12 posts. \(\blacksquare\)
To learn more on optimization problems, we kindly invite to check this verified question: https://brainly.com/question/6348653
are the variables era and number of wins quantitative or categorical variables? why does this matter?
Answers
The variables "era" and "number of wins" are both quantitative variables.
This matters because quantitative variables have numerical values that can be compared and analyzed, while categorical variables are descriptive and non-numerical.
Quantitative variables, such as era and number of wins, have numerical values that can be subjected to mathematical operations and statistical analysis. This distinction is important because it determines the appropriate methods and techniques for data analysis.
For example, with quantitative variables, you can calculate the mean, median, or mode, as well as perform regression analysis or correlation tests. In contrast, categorical variables are analyzed using different methods, such as frequency tables or chi-square tests.
Understanding the difference between quantitative and categorical variables is essential for correctly interpreting data and making informed decisions based on the results of the analysis.
To know more about regression analysis click on below link:
https://brainly.com/question/30011167#
#SPJ11
Plz help me get this right

Answers
Answer:
12 x 8 divided by 2 = 48cm
Step-by-step explanation:
Mr.Franklin drives 37 miles each day to and from work. How many miles does he drive in 20 work days
Answers
Answer:
740
Step-by-step explanation:
37 times 20
Answer:
740 miles
Step-by-step explanation:
37 miles in 1 day
So we need to multiply 37*20 to find the number of miles for 20 days
So, he travels 740 miles
An object is moving with velocity (in ft/sec) v(t)=t2−1t−12
Find the displacement and total distance travelled from t=0 to t=6
Answers
To find the displacement and total distance traveled by the object from t=0 to t=6, we need to integrate the velocity function over the given time interval.
The displacement can be found by integrating the velocity function v(t) with respect to t over the interval [0, 6]. The integral of v(t) represents the net change in position of the object during this time interval.
The total distance traveled can be determined by considering the absolute value of the velocity function over the interval [0, 6]. This accounts for both the forward and backward movements of the object.
Now, let's calculate the displacement and total distance traveled using the given velocity function v(t) = t^2 - (1/t) - 12 over the interval [0, 6].
To find the displacement, we integrate the velocity function as follows:
Displacement = ∫[0,6] (t^2 - (1/t) - 12) dt.
To find the total distance traveled, we integrate the absolute value of the velocity function as follows:
Total distance = ∫[0,6] |t^2 - (1/t) - 12| dt.
By evaluating these integrals, we can determine the displacement and total distance traveled by the object from t=0 to t=6.
Learn more about Velocity here:
brainly.com/question/31968174
#SPJ11
Find the indefinite integral. (Remember to use absolute values where appropriate. Use C for the constant of integration.) integral (1/(xV(4x^2 + 49)) dx
Answers
The indefinite integral is (1÷4)√(4x² + 49) + C.
How we find the indefinite integral of (1÷(x√(4x² + 49))) dx?we will use substitution and include the constant of integration (C) in the final answer.
Perform substitution.Let u = 4x^2 + 49. Then, du/dx = 8x. So, dx = du/(8x).
Rewrite the integral.
Now, we can rewrite the integral as: ∫(1/(x√u)) (du/(8x))
Simplify the integral.
The x terms cancel out: ∫(1/√u) (du/8) = (1/8) ∫(1/√u) du
Solve the integral.
Now, we can find the indefinite integral: (1/8) ∫u^(-1/2) du = (1/8) [2u^(1/2)] + C = (1/4)√u + C
Substitute back the original expression for u.
Finally, substitute u = 4x^2 + 49 back into the expression: (1/4)√(4x² + 49) + C
So, the indefinite integral of (1/(x√(4x^2 + 49))) dx is (1/4)√(4x^2 + 49) + C. Absolute values were not necessary in this case, as the function remains positive for all x values.
Learn more about Indefinite integral
brainly.com/question/29133144
#SPJ11
Do the following using the given information: Utility function u(x1+x2) = .5ln(x1) + .25ln(x₂) .251 Marshallian demand X1 = - and x₂ = P₂ . Find the indirect utility function . Find the minimum expenditure function . Find the Hicksian demand function wwww
Answers
Hicksian demand functions are:x1** = 2P₁x₂ ; x₂** = P₂²
Utility function: u(x1+x2) = .5ln(x1) + .25ln(x₂) .The Marshallian demand functions are: x1* = - and x₂* = P₂.
The indirect utility function is found by substituting Marshallian demand functions into the utility function and solving for v(P₁, P₂, Y).u(x1*,x2*) = v(P₁,P₂,Y) ⇒ u(-, P₂) = v(P₁,P₂,Y) ⇒ .5ln(-) + .25ln(P₂) = v(P₁,P₂,Y) ⇒ v(P₁,P₂,Y) = - ∞ (as ln(-) is not defined)
Thus the indirect utility function is undefined.
Minimum expenditure function can be derived from the Marshallian demand function and prices of goods:
Exp = P₁x1* + P₂x2* = P₁(-) + P₂P₂ = -P₁ + P₂²
Minimum expenditure function is thus:
Exp = P₁(-) + P₂²
Hicksian demand functions can be derived from the utility function and prices of goods:
H1(x1, P1, P2, U) = x1*H2(x2, P1, P2, U) = x2*
Hicksian demand functions are:
x1** = 2P₁x₂
x₂** = P₂²
If there are no restrictions on the amount of money the consumer can spend, the Hicksian demand functions for x1 and x2 coincide with Marshallian demand functions.
Learn more about utility function at:
https://brainly.com/question/32708195
#SPJ11
Consider a hypothetical planet where the gravitational acceleration at the surface is found to be 15.3 m/s2. Calculate the gravitational acceleration at an altitude equal to the planet's diameter.
Answers
By considering the planet's diameter as the distance from its center, we can determine the gravitational acceleration at that altitude. At an altitude equal to the planet's diameter, the gravitational acceleration would be 3.825 m/s² on this hypothetical planet.
The inverse square law of gravity states that the gravitational force decreases as the square of the distance from the center of mass increases.
Since the diameter of the planet is equal to twice the radius, the altitude equal to the planet's diameter is equivalent to being at a distance twice the radius away from the center of mass.
Let's denote the planet's surface gravitational acceleration as "g" and the radius as "R".
Using the inverse square law, we can calculate the gravitational acceleration at an altitude equal to the planet's diameter as follows:
g_altitude = g * (R / (2R))²
= g * (1/4)
= g/4
= 15.3 m/s² / 4
= 3.825 m/s²
Therefore, at an altitude equal to the planet's diameter, the gravitational acceleration would be 3.825 m/s² on this hypothetical planet.
To learn more about law of gravity click here:brainly.com/question/29889712
#SPJ11
Josh started his own lawn maintenance company. He makes $20 on every
lawn that he cuts and his monthly expenses are $325. How many lawns does Josh
need to cut this month so that he can earn a total of $160 after he pays his
monthly expenses?
Answers
How would the one-step equation x/5 = 5 be solved?
Multiply both sides by 1/5
Multiply both sides by the reciprocal of 1/5
Divide 5 by both sides
Divide one side by 5
Answers
Answer:
2nd option
Step-by-step explanation:
Given
\(\frac{x}{5}\) = 5 ( multiply both sides by 5, the reciprocal of \(\frac{1}{5}\) to clear the fraction )
x = 25
Find the measure of arc QS.

Answers
Two vans leave a campground at the
same time. One is traveling north at a
speed that is 10 miles per hour faster
than the other, which is traveling south.
After 2.5 hours, the vans are 255 miles
apart. What is the speed in miles per hour
of the van traveling south?
Answers
Answer:
92 mph
Step-by-step explanation:
Let the speed of the van travelling south
=
v
mph
The distance travelled by the car travelling north is
d
1
=
10
⋅
2.5
=
25
The distance travelled by the car travelling south is
d
2
=
v
⋅
2.5
=
2.5
v
The distance between the cars after
2.5
h
is
d
1
+
d
2
=
255
25
+
2.5
v
=
255
2.5
v
=
255
−
25
=
230
v
=
230
2.5
=
92
mph
The speed is
=
92
mph
Find the mass of a ball of radius R if the mass density is
proportional to the product of the distance to the origin multiplied the distance to a
equatorial plane. Note that:
(i) A ball is a solid whose edge is a sphere.
(ii) An equatorial plane is any plane that contains the center of the sphere.
(iii) It is convenient to look for a coordinate system that facilitates the task. For example, the center of the ball can be placed at the origin. And the equatorial plane?need help with this calculus problem
Answers
The mass of the ball of radius R with the given mass density function is proportional to R^5.
To find the mass of the ball of radius R, we need to use the given mass density function. Let's assume that the center of the ball is at the origin and that the equatorial plane is the xy-plane.
We can use spherical coordinates to express the mass density function in terms of the radial distance, θ and φ. Since the density is proportional to the product of the radial distance and the distance to the equatorial plane, we have:
ρ(r,θ,φ) = kr^2cos(θ)
where k is a constant of proportionality.
The volume element in spherical coordinates is given by:
dV = r^2sin(θ)drdθdφ
To find the mass of the ball, we need to integrate the mass density over the volume of the ball:
M = ∫∫∫ ρ(r,θ,φ) dV
M = ∫∫∫ kr^2cos(θ) r^2sin(θ)drdθdφ
The limits of integration for r are 0 to R, for θ are 0 to π, and for φ are 0 to 2π.
M = k ∫∫∫ r^4cos(θ)sin(θ)drdθdφ from 0 to R, 0 to π, 0 to 2π
This integral can be evaluated using standard techniques. The final answer is:
M = (4/15)πkR^5
The mass of the ball of radius R with the given mass density function is proportional to R^5.
To learn more about sphere visit:
brainly.com/question/11374994
#SPJ11
A carton of grapefruit juice displays the nutritional information shown below. How many grams of sugar are there in a 200 ml glass of juice? Grapefruit juice 250 ml contains Carbohydrate Sugar Protein 19.5 g | 16.5 g | 1.5 g

Answers
Answer:
13.2 g
Step-by-step explanation:
let x = grams sugar in a 200 ml glass
16.5 g sugar / 250 ml = x g sugar / 200 ml
x(250) = (16.5)(200)
x = (16.5)(200) / (250) = 3300 / 250 = 13.2
Answer: there are 13.2 g sugar in a 200 ml glass of juice
Need help please with this

Answers
Answer:
A. 6
B. 48
Step-by-step explanation:
please mark brainliest or leave a heart and rating
Answer:
a. 6
b. 48
Step-by-step explanation:
For a, replace t with 1. 2^1 is 2, and 3 * 2 is 6.
For b, replace t with 4. 2^4 is 16, and 3 * 16 is 48.
Thank me later! 8)
What is the mass of gasoline (density = 0.680 g/cm3 ) in a 94.6 l gasoline tank?
Answers
A 94.6 L gasoline with a density of 0.680 g/cm^3 has a mass of 64328 g.
Density is defined as the ratio between the mass of a substance and the volume it occupies. Denoted by ρ, density is mass per unit volume and the formula is given below:
ρ = mass / volume
Converting first the volume from L to cm^3.
1 L = 1000 cm^3
94.6 L = 94.6(1000 cm^3)
94.6 L = 94,600 cm^3
Given the density of the gasoline and its volume, solve for the mass of the gasoline using the formula for the density.
ρ = mass / volume
0.680 g/cm^3 = mass / 94,600 cm^3
mass = 0.680 g/cm^3 (94,600 cm^3)
mass = 64328 g
mass = 64.328 kg
Learn more about density here: https://brainly.com/question/1354972
#SPJ4
Find the perimeter of the composite figure

Answers
Answer:
88 inches
Step-by-step explanation:
Divide the shape into 2 shapes and add all side lengths.
20+8+8+16+12+24=88
what should be added to {1/-2 - 3/4 of -8/15} so that the sum is the product of -7/50 and 1 1/14 *for grade 7*
Answers
The value that is added on the left-hand side to make the equation equal is -1/100.
What are Mathematical operators?In mathematics, an expression is a group of numbers and operations. The components of a mathematical expression that perform an operation are as follows: multiplication, division, addition, and subtraction.
Given [1/-2 - 3/4 of -8/15],
to add a number so the sum equals the product of -7/50 and 11/14
let the number be x
according to the question,
[1/-2 - 3/4 of -8/15] + x = -7/50*11/14
taking LHS
[1/-2 - 3/4 of -8/15] = -1/2 - (3(-8)/60)
[1/-2 - 3/4 of -8/15] = -1/2 + 24/60
[1/-2 - 3/4 of -8/15] = (-30 + 24)/60
[1/-2 - 3/4 of -8/15] =-6/60 = -1/10
RHS
-7/50*11/14 = -77/700 = -11/100
substitute the values
[1/-2 - 3/4 of -8/15] + x = -7/50*11/14
-1/10 + x = -11/100
x = -11/100 + 1/10
x = (-11 + 10)/100
x = -1/100
Hence -1/100 is added to make the equation equal.
Learn more about Mathematical operators;
https://brainly.com/question/8959976
#SPJ1
-5(m+30)=-17
need help please.. do a step by step for it!
Answers
The value of m is -26.6. The solution has been obtained by using arithmetic operations.
What are arithmetic operations?
In mathematics, "arithmetic operations" refer to the four basic operations that can be used to express any real number. Division, multiplication, addition, and subtraction are the four operations which yields quotient, product, sum and difference respectively.
We are given -5(m + 30) = -17
On solving the equation using the arithmetic operations, we get
⇒-5(m + 30) = -17
⇒-5m - 150 = -17 (On multiplying the bracket by -5)
⇒-5m = 133 (On adding 150 on both the sides)
⇒m = -26.6 (On dividing both the sides by -5)
Hence, we obtained the value of m as -26.6.
Learn more about arithmetic operations from the given link
https://brainly.com/question/30283549
#SPJ1
How many 8-character passwords consisting of uppercase letters, lowercase letters and digits are there that start and end with the same symbol
Answers
Can be cracked within eight hours by the average hacker.
How many 8-character passwords may use both uppercase and lowercase letters?With spaces included in the character count, 8 characters equals between 1 and 2 words. If spaces are excluded from the character count, 8 characters equals between 1 and 3 words.
There are 8-character passwords with capital letters, lowercase letters, and numerals that begin and end with the same symbol.A password of eight characters with just lowercase and capital letters offers 200 billion potential permutations.“1uppercase” is an example of an 8-character password. This password has one uppercase, one lowercase, one number, and one special character.
To learn more about 8-character passwords to refer:
https://brainly.com/question/13543093
#SPJ4
What is the mixed number used to represent 75?
Answers
Answer:
so you cant turn that into a mixed number i dont think
Step-by-step explanation:
if b is the midpoint of ac, ab=12x+11 and bc= 14x - 1, find AB
ik i said i didn't need help with this in my last question but I lied
Answers
Answer:
AB = 83
Step-by-step explanation:
The mid-point of any segment divides the segment into two equal parts
∵ B is the midpoint of segment AC
→ That means B divides AC into two equal segments AB and BC
∴ AB = BC
∵ AB = 12x + 11
∵ BC = 14x - 1
→ Equate them
∴ 14x - 1 = 12x + 11
→ Subtract 12x from both sides
∵ 14x - 12x - 1 = 12x - 12x + 11
∴ 2x - 1 = 11
→ Add 1 to both sides
∵ 2x - 1 + 1 = 11 + 1
∴ 2x = 12
→ Divide both sides by 2
∵ \(\frac{2x}{2}=\frac{12}{2}\)
∴ x = 6
→ To find AB substitute x by 6 in its expression
∵ ab = 12x + 11
∵ x = 6
∴ AB = 12(6) + 11
∴ AB = 72 + 11
∴ AB = 83
Two bank accounts are opened at the same time. The first has a principal of $1000 in an account earning 13% compounded quarterly. The second has a principal $8000 in an account earning 5% interest compounded annually. Determine the number of years, to the nearest tenth, at which the account balances will be equal. t≈ years (Simplify your answer. Type an integer or a decimal. Do not round until the final answer. Then round to the nearest tenth as needed).
Answers
The required number of years at which the account balances will be equal is 4.1 years (to the nearest tenth).
The first bank account has a principal of $1000 earning 13% compounded quarterly.
The second bank account has a principal of $8000 earning 5% compounded annually.
To determine the number of years to the nearest tenth at which the account balances will be equal,We can start by using the compound interest formula,
A = P(1 + r/n)^(nt)
where A = final amount
P = principal (initial amount)
R = rate of interest
N = number of times interest is compounded per year
T = time in years.
Now we have to find the time t when the balance in both accounts is equal.
Thus, we can write:
For the first bank account, A1 = P(1 + r/n)^(nt)
where P = 1000 , r = 13% = 0.13 , n = 4 times compounded per year,
so n = 4t = time
For the second bank account, A2 = P(1 + r/n)^(nt)
where P = 8000 , r = 5% = 0.05 , n = 1 time compounded per year,
so n = 1t = time
At the time when the balances will be equal, A1 = A2, then,
1000(1 + 0.13/4)^(4t)
= 8000(1 + 0.05/1)^(1t)
Solving the above equation for t, we get,
t = 4.1 years.
Hence, the required number of years is 4.1 years (to the nearest tenth).
For more such questions on account visit:
https://brainly.com/question/30813066
#SPJ8
polit, ch 29: effects from individual studies are pooled to yield an estimate of the population effect size by calculating a weighted average of effects. what is often used as the weight?
Answers
The sample size of each study is often used as the weight in pooling the effects to calculate a weighted average of the population effect size.
When conducting a meta-analysis or pooling effects from individual studies, researchers typically assign weights to each study based on certain criteria. The most common weight used is the sample size of each study. The rationale behind using sample size as the weight is that studies with larger sample sizes are considered to provide more precise estimates of the population effect size.
By assigning higher weights to studies with larger sample sizes, the meta-analysis gives more importance to those studies in calculating the overall effect size. This approach accounts for the fact that larger studies tend to have more statistical power and provide more reliable estimates of the true population effect.
The weighted average is calculated by multiplying the effect size of each study by its corresponding weight (usually the sample size), summing up these weighted effects across studies, and dividing by the total weight. This yields an estimate of the population effect size that takes into account the relative contribution of each study based on its sample size.
The weight often used in pooling effects from individual studies to calculate a weighted average of the population effect size is the sample size of each study. Larger sample sizes are assigned higher weights, as they are considered to provide more precise estimates of the true population effect.
To know more about weighted average visit:
https://brainly.com/question/24215541
#SPJ11
Solve the differential equations 2xy(dy/dx)=1 y^2. y(2)=3
Answers
The solution to the given differential equation 2xy(dy/dx) = y², with the initial condition y(2) = 3, is y = (27 * e⁽ˣ⁻²⁾\()^{1/4}\).
To solve the given differential equation
2xy(dy/dx) = y²
We will use separation of variables and integrate to find the solution.
Start with the given equation
2xy(dy/dx) = y²
Divide both sides by y²:
(2x/y) dy = dx
Integrate both sides:
∫(2x/y) dy = ∫dx
Integrating the left side requires a substitution. Let u = y², then du = 2y dy:
∫(2x/u) du = ∫dx
2∫(x/u) du = ∫dx
2 ln|u| = x + C
Replacing u with y²:
2 ln|y²| = x + C
Using the properties of logarithms:
ln|y⁴| = x + C
Exponentiating both sides:
|y⁴| = \(e^{x + C}\)
Since the absolute value is taken, we can remove it and incorporate the constant of integration
y⁴ = \(e^{x + C}\)
Simplifying, let A = \(e^C:\)
y^4 = A * eˣ
Taking the fourth root of both sides:
y = (A * eˣ\()^{1/4}\)
Now we can incorporate the initial condition y(2) = 3
3 = (A * e²\()^{1/4}\)
Cubing both sides:
27 = A * e²
Solving for A:
A = 27 / e²
Finally, substituting A back into the solution
y = ((27 / e²) * eˣ\()^{1/4}\)
Simplifying further
y = (27 * e⁽ˣ⁻²⁾\()^{1/4}\)
Therefore, the solution to the given differential equation with the initial condition y(2) = 3 is
y = (27 * e⁽ˣ⁻²⁾\()^{1/4}\)
To know more about differential equation:
https://brainly.com/question/2273154
#SPJ4
Which verbal expression best describes the algebraic expression 2x ÷ 4? (4 points) Group of answer choices The quotient of two and some number times four The sum of two and some number divided by four The quotient of two times some number and four The product of some number and four divided by two
Answers
Answer:
C. The quotient of two times some number and four
Step-by-step explanation:
Given the expression 2x÷4
The x be the unknown number.
2x can be written as:
Product of some number and 2 OR two times an unknown number
2x÷4 will then be written as:
The quotient of two times a number and 4
The correct option to describe the equation is "The quotient of two times some number and four"