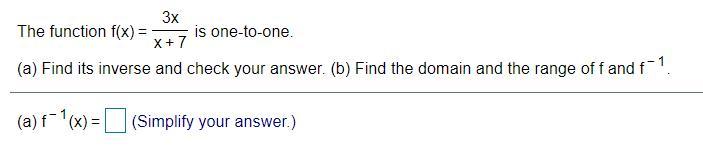
Find its inverse and check your answer. (b) Find the domain and the range of f and
Answers
We have the function:
f(x) = 3x / (x + 7)
(a)
We rename the function as: f(x) = y
Then:
y = 3x / (x + 7)
Taking the inverse:
1/y = (x + 7) / 3x
1/y = x/3x + 7/3x
1/y = 1/3 + 7/3x
Solving for x:
1/y - 1/3 = 7/3x
1/x = 3/7y - 1/7 = (3 - y) / 7y
Taking the inverse:
x = 7y / (3 - y)
Then, the inverse function of f is:
f ⁻¹(x) = 7x / (3 - x)
(b)
We know that the division by 0 is undefined in real numbers. From the function f, we have a division by 0 if x = -7, so the domain should be:
Dom_f = {x| x ≠ -7}
For the range, we know that x = -7 is a vertical asymptote of the function f, so this means that the graph never passes across x = -7, but it tends to it on infinity. Then, the range of f is:
Ran_f = All the real numbers
For f ⁻¹(x), we see that for x = 3 there is a division by 0, so this is an asymptote of the function. Then, the domain of f ⁻¹ is:
Dom_f ⁻¹ = {x| x ≠ 3}
Again, as there is an asymptote, the range is:
Ran_f ⁻¹ = All the real numbers
Related Questions
Can someone please walk me through this?
3x-1=4x+8-x
Answers
3x-1=4x+8-x
3x -4x +x = 8+1
4x -4x = 9
0x =9
x= 9/0 which is undefined .
1. In part (b) of the example, why isn't AB a correct answer? 2. In part (c) of the example, would KJL be an appropriate answer?

Answers
Answer:
Step-by-step explanation:
1. AB isn't a correct answer because it only refers to the part of the line between point A and point B. This is incorrect because it doesn't represent the whole line which goes on infinity past point A (as seen by the arrow).
2. KJL would not be an appropriate answer because the points must be listed in the same order that they appear in direction of the line. The angle shown is angle K so K should be the middle letter as it is the middle point with the angle. KJL would not be appropriate because it would refer to the angle J if there was another line between J and L.
Hope this helped!
If the m = and the b = -2. then the linear equation is:
y = x + 2.
y = x − 2.
y = 2x.
None of these choices are correct.
Answers
Hey there! I'm happy to help!
The linear equation with m and b is called the slope intercept equation, where m is the slope and b is the y intercept. It is written as y=mx+b.
We see that m is equal to 1 and b is equal to -2. We can write this down as y=1x-2, or just y=x-2 as 1x is just x.
Have a wonderful day! :D
una escuela debe transportar 200 estudiantes
Answers
Answer: a school must transport 200 students
Step-by-step explanation:
Given the two functions, which statement is true? f(x) = 3x, g(x) = 3x + 5 Question 12 options: g(x) is translated up 5 units compared to f(x) g(x) is translated left 5 units compared to f(x) g(x) is translated down 5 units compared to f(x) g(x) is translated right 5 units compared to f(x)
Answers
The correct statement is: g(x) is translated up 5 units compared to f(x).
The correct answer is A.
To determine the translation between the two functions, we can observe that the only difference between them is the constant term.In f(x) = 3x, there is no constant term, so the graph of f(x) passes through the origin (0, 0).In g(x) = 3x + 5, there is a constant term of 5 added to the function. This means that the graph of g(x) is shifted vertically upward by 5 units compared to the graph of f(x).Therefore, g(x) is translated up 5 units compared to f(x).The correct answer is A.
For such more questions on translated
https://brainly.com/question/12861087
#SPJ8
Factor 4x2 + 24x + 36.
A) 4(x + 3)(x + 3)
B) 4(x + 6)(x – 6)
C) (4x + 3)(x + 3)
D) (2x – 6)(2x – 6)
Answers
Answer:
\(\huge\boxed{\text{A) } 4(x+3)(x+3) }\)
Step-by-step explanation:
In order to factor this, we need to factor out a common term and then solve for x.
We can see that we can factor out a 4 from this entire equation as each term is a multiple of 4.
This leaves us with \(4(x^2+ 6x + 9)\).
We can now solve for x for the expression in the parentheses, \(x^2 +6x + 9\).
To solve for x, we can use the XBOX method. This tells us that:
When the two roots are added, they will equal b (in this case, 6) When the two roots are multiplied, they will equal c (in this case 9)Experimenting with some numbers gets us with 3 and 3 - 3+3 = 6 and 3*3 = 9.
Therefore, our roots will be \((x+3)(x+3)\).
Putting that back into the factorization of our original expression, that leaves us with \(4(x+3)(x+3)\).
Hope this helped!
A manufacturer must test that his bolts are 4.00 cm long when they come off the assembly line. He must recalibrate his machines if the bolts are too long or too short. After sampling 121 randomly selected bolts off the assembly line, he calculates the sample mean to be 4.21 cm. He knows that the population standard deviation is 0.83 cm. Assuming a level of significance of 0.02, is there sufficient evidence to show that the manufacturer needs to recalibrate the machines? Step 2 of 3: Compute the value of the test statistic. Round your answer to two decimal places.
Answers
The sample mean of 4.21 cm is significantly different from the specified target mean of 4.00 cm.
Step 1: State the hypotheses.
- Null Hypothesis (H₀): The mean length of the bolts is 4.00 cm (μ = 4.00).
- Alternative Hypothesis (H₁): The mean length of the bolts is not equal to 4.00 cm (μ ≠ 4.00).
Step 2: Compute the value of the test statistic.
To compute the test statistic, we will use the z-test since the population standard deviation (σ) is known, and the sample size (n) is large (n = 121).
The formula for the z-test statistic is:
z = (X- μ) / (σ / √n)
Where:
X is the sample mean (4.21 cm),
μ is the population mean (4.00 cm),
σ is the population standard deviation (0.83 cm), and
n is the sample size (121).
Plugging in the values, we get:
z = (4.21 - 4.00) / (0.83 / √121)
z = 0.21 / (0.83 / 11)
z = 0.21 / 0.0753
z ≈ 2.79 (rounded to two decimal places)
Step 3: Determine the critical value and make a decision.
With a level of significance of 0.02, we perform a two-tailed test. Since we want to determine if the mean length of the bolts is different from 4.00 cm, we will reject the null hypothesis if the test statistic falls in either tail beyond the critical values.
For a significance level of 0.02, the critical value is approximately ±2.58 (obtained from the z-table).
Since the calculated test statistic (2.79) is greater than the critical value (2.58), we reject the null hypothesis.
Conclusion:
Based on the computed test statistic, there is sufficient evidence to show that the manufacturer needs to recalibrate the machines. The sample mean of 4.21 cm is significantly different from the specified target mean of 4.00 cm, indicating that the machine's output is not meeting the desired length. The manufacturer should take action to recalibrate the machines to ensure the bolts meet the required length of 4.00 cm.
for more such question on mean visit
https://brainly.com/question/1136789
#SPJ8
. Order the following numbers from least to greatest: 3√2 , √3 − 1, √19 + 1, 6,
2√10 ÷ 5 and √14.
pls someone help me
Answers
The required order from least to greatest is √3 − 1, 2√10 ÷ 5, √14, 3√2, √19 + 1 and 6
What is ascending order?An arrangement of numbers in which the numbers are arranged from smallest to greatest numbers is called ascending order.
Given that, some numbers, 3√2, √3 − 1, √19 + 1, 6, 2√10 ÷ 5 and √14.
We need to order them from least to greatest,
3√2 = 4.24
√3 − 1 = 0.73
√19 + 1 = 5.35
6
2√10 ÷ 5 = 1.26
√14 = 3.74
The order from least to greatest is :-
0.73, 1.26, 3.74, 4.24, 5.35 and 6
i.e.
√3 − 1, 2√10 ÷ 5, √14, 3√2, √19 + 1 and 6
Hence, the required order from least to greatest is √3 − 1, 2√10 ÷ 5, √14, 3√2, √19 + 1 and 6
Learn more about ascending order, click;
https://brainly.com/question/28762233
#SPJ9
Please answer this in two minutes

Answers
Answer: (5, 19)
Step-by-step explanation:
19 - 12 = 7
8 - 13.5 = -5.5
Use this formula for M to find T
12 - 7 = 5
13.5 + 5.5 = 19
(5, 19)
Write this number in standard form 3 thousands, 16 tens,7 ones
Answers
Archie bought 100 shares of stock in an ice cream company 2 years ago. He paid $60.65 per share. He just sold all of his shares for $67.68 per share. How much did he gain?
Answers
Answer:
Step-by-step explanation:
First, we need to find the difference between the price that he sold the shares for and the price that he bought them at: (67.68-60.65) = 7.03
That means that there was a gain of $7.03 per share for Archie.
That being said, since Archie bought 100 shares, we can multiply that number by 100 to find the total gain from selling the shares:
(7.03x100)= 703
The answer then is:
Archie gained $703 from selling all of his shares.
Find sin 2x, cos 2x, and tan 2x if sinx =
5
13
and x terminates in quadrant I.
ala
sin 2x
U
х
cos 2x
=
tan 2x
10

Answers
Answer:
12/13 ; 5/13; 12/5
Step-by-step explanation:
sinx =5/13 =opposite/ hypothenus
By Pythagoras rule the hypothenus side can be obtained as
√ 13^2 -5^2 = √169 -25 = √144 = 12
cos x= adjacent/ hypothenus = 12/13
Now Cos2x= Sinx
And Sin2x = Cosx
Hence ;
Sin2x=12/13
Cos2x =5/13
Tan2x= Sin 2x/ Cos 2x
= 12/13 ÷ 5/13
= 12/13 × 13/5 = 12/5
Which of these can be the graph of the equation

Answers
Answer: It's letter A, because it's slope-intercept form.
Step-by-step explanation:
|| evaluate. ||
m/ 2 for m = 8
help asap plsplspls !! :)
Answers
Answer:
4
Step-by-step explanation:
8/2=4
The blank is a plot of paired data (x,y) and is helpful in degerming whether there is a relationship between the two variables 
Answers
Step-by-step explanation:
Scatter plot is the correct answer
1. Find the equation of the image of the circle x² + y2 + 16x-24y + 183 = 0 by rotated the line mirror 4x + 7y + 13 = 0. 2. The image of the circle (x - 3)² + (y-2)² = 1 in the line mirror ax + by = 19 is (x-1)³ + (y-16)2 = 1 then, find the values of (a, b). 3. Find the equation of a line passing through the origin and making an angle with the 4 line y-3x-5. 4. A parabola is drawn with its focus at (3,4) and vertex at the focus of the parabola y²-12x - 4y + 4 = 0. The n find equation of the parabola. 5. If the line ax + by + c = 0 touches the circle x² + y² - 2x = and is normal to the circle x² + y² + 2x - 4y + 1 = 0, then find the value of (a, b). 6. If the line through the points (-2, 6) and (4, 8) is perpendicular to the line through the points (8, 12) and (x, 24). Find the value of x. -3 7.1² 14 231= [] then find the matrix A 8. Find the equation of the ellipse having its center at the point (2,-3), one and one vertex at (4, -3). 3 9. Find the value of x if-1 0 10. Solve the linear system using Cramer's rule a) 2 1 2 4 (6x - 4y = -12 8x - 3y = -2 X = 16 -21 3x + 2y = z = 5 b) x-y+3z = -15 (2x + y +7z = -28 one focus at (3,-3) 11. Find the value of k for which the following system of linear equations has infinite solutions: x + (k+1)y = 5 ((k+1)x + 9y = 8k - 1
Answers
Answer:
-72x - 53y + 287 = 0.
Step-by-step explanation:
To find the equation of the image of the circle, we need to reflect each point on the circle in the given line mirror.
The line mirror equation is given as 4x + 7y + 13 = 0.
The reflection of a point (x, y) in the line mirror can be found using the formula:
x' = (x - 2Ay - 2B(Ax + By + C)) / (A^2 + B^2)
y' = (y - 2Bx + 2A(Ax + By + C)) / (A^2 + B^2)
where A, B, and C are the coefficients of the line mirror equation.
For the given line mirror equation 4x + 7y + 13 = 0, we have A = 4, B = 7, and C = 13.
Now, let's find the equations of the image of the circle.
The original circle equation is x² + y² + 16x - 24y + 183 = 0.
Using the reflection formulas, we substitute the values of x and y in the circle equation to find x' and y':
x' = (x - 2Ay - 2B(Ax + By + C)) / (A^2 + B^2)
= (x - 2(4)y - 2(7)(4x + 7y + 13)) / (4^2 + 7^2)
= (x - 8y - 8(4x + 7y + 13)) / 65
= (x - 8y - 32x - 56y - 104) / 65
= (-31x - 64y - 104) / 65
y' = (y - 2Bx + 2A(Ax + By + C)) / (A^2 + B^2)
= (y - 2(7)x + 2(4)(Ax + By + C)) / (4^2 + 7^2)
= (y - 14x + 8(Ax + By + C)) / 65
= (y - 14x + 8(4x + 7y + 13)) / 65
= (57x + 35y + 104) / 65
Therefore, the equation of the image of the circle is:
(-31x - 64y - 104) / 65 + (-57x + 35y + 104) / 65 + 16x - 24y + 183 = 0
Simplifying the equation, we get:
-31x - 64y - 57x + 35y + 16x - 24y + 183 + 104 = 0
-72x - 53y + 287 = 0
So, the equation of the image of the circle is -72x - 53y + 287 = 0.
What is the domain of y = 4 log5 (x - 3)?
A. all real numbers
B. all real numbers greater than 4
C. all real numbers greater than 5
D. all real numbers greater than 3.
Answers
The domain of \(y=4\log_5(x-3)\) is (d) all real numbers greater than 3.
How to determine the domain?The function is given as:
\(y=4\log_5(x-3)\)
Set the expression in bracket greater than 0
x -3 > 0
Add 3 to both sides
x > 3
Hence, the domain of \(y=4\log_5(x-3)\) is (d) all real numbers greater than 3.
Read more about domain at:
https://brainly.com/question/1770447
#SPJ1
From a point on the ground 12 feet from the base of a flagpole, the angle of elevation of the top of the pole measures 55. How tall is the flagpole?
Answers
Answer:
the flagpole is 16 feet tall.
Step-by-step explanation:
A right angle triangle is formed.
The distance of the point on the ground from the base of the flagpole represents the adjacent side of the right angle. The height of the flagpole from the ground represents the opposite side of the right angle.
To determine the height, h of the flagpole, we would apply the Tangent trigonometric ratio.
Tan θ, = opposite side/adjacent side. Therefore,
Tan 53 = h/12
h = 12Tan53 = 12 × 1.327
h = 16 feet to the nearest whole number
How much would you need to deposit in an account now in order to have $3000 in the account in 10 years? Assume the account earns 8% interest compounded quarterly. Round your answer to the nearest cent.
Answers
We can use the formula for compound interest to solve this problem:
A = P(1 + r/n)^(nt)
where A is the amount of money in the account after t years, P is the principal (the initial amount deposited), r is the interest rate, n is the number of times the interest is compounded per year, and t is the time in years.
We want to find the amount of money that needs to be deposited now (P) in order to have $3000 in the account after 10 years, so we can rearrange the formula to solve for P:
P = A / (1 + r/n)^(nt)
Plugging in the given values, we get:
P = 3000 / (1 + 0.08/4)^(4*10)
P = 3000 / 2.208756...
P = $1358.39 (rounded to the nearest cent)
Therefore, you would need to deposit $1358.39 in the account now in order to have $3000 in the account in 10 years at an 8% interest rate compounded quarterly.
*IG: whis.sama_ent*
What is the ratio of the calories Robyn
burned on Wednesday le the celories she
burned on Monday?
Answers
Question isn't complete but we make assumptions in order to complete the question and explain
Answer and explanation:
If we are given a table on calories burned by Robyn on weekdays from Monday to Friday and on this table Robyn burnt 500 calories on Monday and burnt 400 calories on Wednesday, then we are required to determine the ratio of calories burnt on Wednesday to calories burnt on Monday:
Calories burnt on Wednesday = 400
Calories burnt on Monday =500
Ratio of calories burnt on Wednesday to calories burnt on Monday =400/500=4/5
Ratio =4:5
an academic department has just completed voting by secret ballot for a department head. the ballot box contains four slips with votes for candidate a and three slips with votes for candidate (a) List all possible outcomes. This answer has not been graded yet. (b) Suppose a running tally is kept as slips are removed.
Answers
Therefore , the solution of the given problem of probability comes out to be AAAABBB (4 ballots for candidate A, 3 votes for candidate B) (4 votes for candidate A, 3 votes for candidate B)
What is probability?The primary objective of statistical inference, a branch of mathematics, is to determine the chance that a claim is true or that a specific event will occur. Chance can be represented by any number between 0 and 1, in which 1 typically represents certainty and 0 typically represents possibility. A probability diagram shows the chance that a specific event will occur.
Here,
(a) The voting box contains a total of seven slips, four of which are for candidate A and three for candidate B. Thus, there are 35 events that can occur from 7 choose 4 (or 7 choose 3) options.
Each vote can be represented by a letter, with A standing for a vote for candidate A and B for candidate B, so that all outcomes can be listed. These are the potential results:
AAAA
AAAB
AABA
ABAA
BAAA
AABB
ABAB
BABA
BBAA
ABBB
BABB
BBAB
BBBA
(b)
For instance, the following results could occur if the slips were removed in the following order:
A (1 vote for contender A) (1 vote for candidate A)
AA (2 ballots for candidate A) (2 votes for candidate A)
AAB (2 ballots for candidate A, 1 vote for candidate B) (2 votes for candidate A, 1 vote for candidate B)
AAAB (3 ballots for candidate A, 1 vote for candidate B) (3 votes for candidate A, 1 vote for candidate B)
AAAAB (4 ballots for candidate A, 1 vote for candidate B) (4 votes for candidate A, 1 vote for candidate B)
AAAABB (4 ballots for candidate A, 2 votes for candidate B) (4 votes for candidate A, 2 votes for candidate B)
AAAABBB (4 ballots for candidate A, 3 votes for candidate B) (4 votes for candidate A, 3 votes for candidate B)
To know more about probability visit:
https://brainly.com/question/11234923
#SPJ4
A truck travels along a highway. Its distance from the exit, as a function of
time, is modeled by y= -50x+ 75.

Answers
Answer:
B
Step-by-step explanation:
it's not the other options, and it only contains one variable with constant change
Answer:
b
Step-by-step explanation:
Rick shoots a basketball at an angle of 60' from the horizontal. It leaves his hands 6 feet from the ground with a velocity of 25 ft/s.Step 1 of 2: Construct a set of parametric equations describing the shot. Answer

Answers
Solution:
Given:
\(\begin{gathered} Initial\text{ velocity,}u=25ft\text{ /s} \\ \theta=60^0 \end{gathered}\)
The parametric equations are gotten by first resolving the velocity into horizontal and vertical components.
Recall;
\(\begin{gathered} speed=\frac{distance}{time} \\ distance=speed\times time \end{gathered}\)Hence, the parametric equations are:
\(\begin{gathered} x=(25cos60)t \\ y=(25sin60)t+6 \end{gathered}\)5t+7+8b
I need also help on -2(x+3)=_-6
Answers
The solution to the equation -2(x + 3) = -6 is x = 0.
To simplify the expression 5t + 7 + 8b, we can combine like terms.
There are two like terms in the expression: 5t and 8b.
Combining the like terms gives us:
5t + 8b + 7
Therefore, the simplified form of the expression 5t + 7 + 8b is 5t + 8b + 7.
Regarding the equation -2(x + 3) = -6:
To solve this equation, we can follow these steps:
Distribute the -2 to the terms inside the parentheses:
-2 * x + (-2) * 3 = -6
This simplifies to:
-2x - 6 = -6
Move the constant term to the right side by adding 6 to both sides of the equation:
-2x = 0
Divide both sides of the equation by -2 to isolate the variable x:
x = 0 / -2
Simplifying the right side of the equation gives us:
x = 0
The solution to the equation -2(x + 3) = -6 is x = 0.
The simplified expression 5t + 7 + 8b remains as 5t + 8b + 7, and the solution to the equation -2(x + 3) = -6 is x = 0.
For more questions on equation
https://brainly.com/question/17145398
#SPJ8
find the positive suare root of the following number 57.27
Answers
The positive square root of 57.27 is approximately 7.5726, with further decimal places available through iterative approximation methods.
To find the positive square root of the number 57.27, we can use a calculator or mathematical operations.
Taking the square root of a number involves finding a value that, when multiplied by itself, gives the original number. In this case, we want to find the value that, when squared, equals 57.27.
Using a calculator, we can find the square root of 57.27 as approximately 7.5726. However, it's important to note that this is an approximation and may not be completely accurate due to rounding errors.
If we want to find a more precise answer manually, we can use iterative approximation methods. One such method is the Newton-Raphson method, which involves repeatedly refining an initial guess.
Starting with an initial guess of, let's say, 7, we can use the formula:
x(n+1) = (x(n) + (57.27/x(n)))/2,
where x(n) is the current approximation and x(n+1) is the next approximation. Iterating this formula a few times will converge to a more accurate value.
After a few iterations, we find that the positive square root of 57.27 is approximately 7.572615. This value can be further refined by performing more iterations or using more advanced numerical methods.
For more such questions on positive square root visit;
https://brainly.com/question/14474761
#SPJ8
If the measure of angle A=55 degrees, b=12, and c = 7 then find the measure of angle B.

Answers
Answer:
use the sine rule
Step-by-step explanation:
One urn contains 7 blue balls and 13 white balls, and a second urn contains 14 blue balls and 5 white balls. An urn is selected at random, and a ball is chosen from the urn. (a) Let B, be the event that the first urn is chosen, B, be the event that the second urn is chosen, and A be the event that the chosen ball is blue. Find each of the following. P(A | B1) P(A | B2) P(A n B2) P(A n B2) What is the probability (as a %) that the chosen ball is blue? (Round your answer to one decimal place.) % (b) If the chosen ball is blue, what is the probability (as a %) that it came from the first urn? (Round your answer to one decimal place.)
Answers
The probability that the chosen ball is blue is 55.3%.
If the chosen ball is blue, the probability would be 3.33% that it came from the first urn.
Probability is a measure of the likelihood of an event occurring. It is a number between 0 and 1, with 0 representing an impossible event and 1 representing a certain event. The probability of an event is calculated by dividing the number of ways the event can occur by the total number of possible outcomes.
(a) To find P(A|B1), we use the formula P(A|B) = P(A and B)/P(B).
In this case, P(A and B1) is the probability of choosing a blue ball from the first urn, which is 7/20.
The probability of choosing the first urn is 1/2, so P(B1) = 1/2.
Plugging these values into the formula gives us P(A|B1) = (7/20)/(1/2) = 14/20 = 7/10.
To find P(A|B2), we use the same formula.
In this case, P(A and B2) is the probability of choosing a blue ball from the second urn, which is 14/19.
The probability of choosing the second urn is 1/2, so P(B2) = 1/2.
Plugging these values into the formula gives us P(A|B2) = (14/19)/(1/2) = 28/19.
To find P(A and B2), we use the formula P(A and B) = P(A|B) * P(B).
In this case, we already know that P(A|B2) = 28/19 and P(B2) = 1/2, so P(A and B2) = (28/19) * (1/2) = 28/38.
To find P(A or B2), we use the formula P(A or B) = P(A) + P(B) - P(A and B).
In this case, P(A) is the probability of choosing a blue ball overall, which is 21/38.
P(B2) is the probability of choosing the second urn, which is 1/2.
P(A and B2) is the probability of choosing a blue ball from the second urn, which is 28/38.
Plugging these values into the formula gives us P(A or B2) = 21/38 + 1/2 - 28/38 = 15/38.
The probability that the chosen ball is blue is P(A) = 21/38 = 55.3%.
(b) If the chosen ball is blue, the probability that it came from the first urn is P(B1|A) = P(B1 and A)/P(A).
We already know that P(B1 and A) is the probability of choosing a blue ball from the first urn, which is 7/20.
We also know that P(A) is the probability of choosing a blue ball overall, which is 21/38.
Plugging these values into the formula gives us P(B1|A) = (7/20)/(21/38) = 7/21.
This probability is equal to 33.3%.
Learn more about probability, here https://brainly.com/question/29582649
#SPJ4
Find the 16th term of the arithmetic sequence 4, 9,14, 19
Answers
The 16th term of the given arithmetic sequence 4, 9, 14, 19... is 79.
The n-th term of an arithmetic sequence, with the first term as a, and the common difference as d, is calculated using the formula:
aₙ = a + (n - 1)d.
In the question, we are asked to find the 16th term of the arithmetic series 4, 9, 14, 19...
The first term of the given arithmetic sequence, a = 4.
The common difference of the given arithmetic sequence, d = 5.
The term to be computed, n = 16.
Therefore, the 16th term of the arithmetic sequence 4, 9, 14, 19... using the formula of the n-th term as aₙ = a + (n - 1)d, can be shown as:
a₁₆ = 4 + (16 - 1)5,
or, a₁₆ = 4 + 15*5,
or, a₁₆ = 4 + 75,
or, a₁₆ = 79.
Thus, the 16th term of the given arithmetic sequence 4, 9, 14, 19... is 79.
Learn more about an arithmetic sequence at
https://brainly.com/question/20671618
#SPJ1
1
Given: - 2 x > 6.
Choose the solution set.
O{x|xER, x>-12}
{x|xER, x>-3}
{x|xER,x<-3}
(xxER, x < -12}

Answers
Answer:
x< -12
Step-by-step explanation:
-1/2x>6
x-2. x-2
x>-12
Since we multiply by we negative we flip the sign
x< -12
Hopes this helps
How many 134 minutes is equal to a hour