encuentra tres fraccion equivalente en cada caso *36/20 *-1/4 *50/40 *-5/-6
Answers
Answer:
nose pero ayúdame
Step-by-step explanation:
acupo ayuda
Related Questions
which point is located at 5_2

Answers
Hey there!
Point D is located at point (5, -2)
In coordinates, the first number represents the x-coordinate, and the second number represents the y-coordinate. (TIP: YOU MUST START AT THE ORIGIN, OR (0, 0). In the x-coordinate, you go left/right that number of spaces, left for negative and right for positive. For the y-coordinate, you go up/down that number of spaces, down for negative and up for positive. This means that the point (5, -2) is 5 units right and 2 units down, which lands on point D.
Hope it helps and have an amazing day!
Change the fraction to an equivalent fraction using multiplication.
\(\frac{5}{7}=\frac{?}{21}\)
Answers
Answer:
\(\frac{5}{7\\}\) * \(\frac{3}{3}\) = \(\frac{15}{21}\)
Step-by-step explanation:
To get an equivalent fraction, we multiply by a fraction that is equal to one. The purpose is to alter the denominator of the fraction. To get from a denominator of 7 to 21 we multiply by 3. Therefore we will multiply 5/7 by 3/3 to get the new equivalent fraction with a denominator of 21.
Answer:
a0 - 15
Step-by-step explanation:
If A and B are mutually exclusive events with P(A) = 0.4 and P(B) = 0.5, then P(A ∩ B) =
a. 0.10
b. 0.90
c. 0.00
d. 0.20
Answers
The probability of A and B occurring simultaneously (P(A ∩ B)) is c. 0.00.
In this scenario, A and B are stated to be mutually exclusive events. Mutually exclusive events are events that cannot occur at the same time. This means that if event A happens, event B cannot happen, and vice versa.
Given that P(A) = 0.4 and P(B) = 0.5, we can deduce that the probability of A occurring is 0.4 and the probability of B occurring is 0.5. Since A and B are mutually exclusive, their intersection (A ∩ B) would be an empty set, meaning no outcomes can be shared between the two events. Therefore, the probability of A and B occurring simultaneously, P(A ∩ B), would be 0.
To further clarify, let's consider an example: Suppose event A represents flipping a coin and getting heads, and event B represents flipping the same coin and getting tails. Since getting heads and getting tails are mutually exclusive outcomes, the intersection of events A and B would be empty. Therefore, the probability of getting both heads and tails in the same coin flip is 0.
In this case, since events A and B are mutually exclusive, the probability of their intersection, P(A ∩ B), is 0.
Therefore, the correct answer is: c. 0.00
Learn more about Probability
brainly.com/question/795909
#SPJ11
when you are designing a research study and considering what hypothesis test you might use, a common rule of thumb is to select the most powerful test. why is this a good idea? the most powerful test is the test most likely to reject the null hypothesis when it is false the most powerful test is the test least likely to result in a type i error. the most powerful test is the test least likely to reject the null hypothesis. the most powerful test is the test most likely to get the right answer.
Answers
The correct answer is, the most powerful test is the test least likely to result in a Type II error.
What is probability?
The area of mathematics known as probability deals with numerical descriptions of how likely it is for an event to happen or for a claim to be true. A number between 0 and 1 is the probability of an event, where, broadly speaking, 0 denotes the event's impossibility and 1 denotes its certainty.
In terms of hypothesis testing, the power of a test is given by the probability of rejecting a null hypothesis when it is actually false.
Also, we know that we commit a type II error when we don't reject the null hypothesis when it is actually false.
So, combining these two facts, we can infer that the most powerful test is the test where we have a high probability of rejecting a null hypothesis when it is actually false. This means that the most powerful test is given by the test that will have almost no or absolutely no type II error.
Hence, the most powerful test is the test least likely to result in a Type II error.
To know more about probability, click on the link
https://brainly.com/question/24756209
#SPJ4
the quotient of a number and 7 is greater than or equal to 20
Answers
Answer:
a is greater than or equal to 140
Step-by-step explanation:
Multiply both sides by 7, which cancels out the 7 and turns 20 into 140
Consider a renewal process with mean interarrival time μ. Suppose that each event of this process is independently "counted" with probability p. Let NC(t) denote the number of counted events by time t,t>0 . (a) Is NC(t),t⩾0 a renewal process? (b) What is limt→[infinity]NC(t)/t?
Answers
a) NC(t) is not a renewal process.
b) The limit of NC(t)/t as t approaches infinity is equal to p/μ.
(a) To determine whether NC(t), t ⩾ 0, is a renewal process, we need to check whether it satisfies the two defining properties of a renewal process: (1) the interarrival times between consecutive events are independent and identically distributed, and (2) the interarrival times follow the same probability distribution as the original renewal process.
In this case, the interarrival times between consecutive counted events are not independent, because the presence of one event affects the probability of the next event being counted. Therefore, NC(t) is not a renewal process.
(b) To find the limit of NC(t)/t as t approaches infinity, we can use the law of large numbers, which states that the sample mean of independent and identically distributed random variables converges to the expected value of the random variable as the sample size increases.
Since each event is independently counted with probability p, the expected number of counted events by time t is p(t/μ). Therefore, by the law of large numbers, we have:
limt→∞ NC(t)/t = limt→∞ [p(t/μ)]/t = p/μ
To know more about probability here
https://brainly.com/question/11234923
#SPJ4
3. a committee of 4 is to be selected from a group of 12 people. how many possible committees can be selected?
Answers
According to combinations formula there are 495 possible committees that can be selected from a group of 12 people.
To calculate this, you can use the formula for combinations
nCr = n!/(r!(n-r)!)
where n is the total number of people (12) and r is the number of people on the committee.
Therefore, the possible number of committees that can be selected is;
= {12!}/{4!8!}
= 12*11*10*9/4*3*2*1
= 11880/24
= 495
Therefore, 495 possible committees can be selected from a group of 12 people if a committee of 4 is to be selected.
Know more about combinations here:
https://brainly.com/question/28065038
#SPJ11
A dairy farmer milks his two cows every day. He determined the chance that he gets anywhere between 12 and 14 gallons of milk in one day is around 32%. Identify the method of probability the farmer used to reach this conclusion. Select the correct answer below: theoretical relative frequency
Answers
The dairy farmer used the relative frequency method of probability to reach his conclusion.
Relative frequency is a method of calculating probability that is based on the observation of how often an event occurs in a sample. The farmer likely observed how often he gets between 12 and 14 gallons of milk in a day and used that data to calculate the probability of it happening.
In contrast, theoretical probability is based on the assumption that all possible outcomes are equally likely. It is calculated by dividing the number of desired outcomes by the total number of possible outcomes.
Therefore, the correct answer is relative frequency.
Know more about relative frequency here:
https://brainly.com/question/29739263
#SPJ11
coordinate grid by equation y=4 what line would represent a row parallel to it ?
Answers
A row parallel to the line y = 4 on a coordinate grid would be represented by a line with an equation of the form y = c.
How to find a row parallel to y=4 on a coordinate grid?A coordinate grid is a two-dimensional plane consisting of a horizontal x-axis and a vertical y-axis. The point where the x and y-axes intersect is called the origin, and it has coordinates (0, 0).
An equation in the form y = c, where c is a constant, represents a horizontal line parallel to the x-axis. In this case, the equation y = 4 represents a horizontal line that intersects the y-axis at 4, as all points on the line have a y-coordinate of 4.
To find a row parallel to this line, we need to look for another line that also has a constant y-coordinate of 4. One way to represent this line is by the equation y = 4 again, since all points on this line have a y-coordinate of 4.
Alternatively, we can look for an equation in the form y = mx + b, where m is the slope of the line (which is zero for a horizontal line), and b is the y-intercept (which is 4 in this case). Thus, the equation for the row parallel to y = 4 would also be y = 4, since its slope is zero and it intersects the y-axis at y = 4, just like the line y = 4.
Learn more about coordinate grid
brainly.com/question/17597121
#SPJ11
HELP ME A square pyramid is shown:
A square pyramid is shown. The sides of the square base are labeled 0.6 foot. The height of one of the triangular sides is labeled 7 feet.
What is the surface area of the pyramid? (1 point)
a
2.46 square feet
b
8.76 square feet
c
5.16 square feet
d
1.56 square feet
Answers
Answer:
B. 8.76 square feet------------------------
Each triangle face has height of 7 ft and base of 0.6 ft and the base of the pyramid is the square with side of 0.6 ft.
Total surface area includes a square base and four triangular faces and the measure of it is:
S = 0.6² + 4*(1/2)*0.6*7 = 0.36 + 8.4 = 8.76 ft²The matching choice is B.
Solve the following system of equations using substitution (Enter your answer as an ordered pair, including the parentheses and comma.)
-3x+6y=12
2y=x+4
Answers
The system of equations has infinite solutions, both equations represent the same line.
How to solve the system of equations?
Here we have the following system of equations:
-3x+6y=12
2y=x+4
And we want to solve this by substitution, first, we can rewrite the first equation as:
-3x + 3*(2y) = 12
Now we can substitute the second equation 2y = x + 4 in the parenthesis, we will get:
-3x + 3*(x + 4) = 12
Now we can solve this for x.
-3x + 3x + 12 = 12
12 = 12
So this is true for any value of x, which means that both equations represent the same line (thus the system has infinite solutions).
Learn more about systems of equations:
https://brainly.com/question/13729904
#SPJ1
True or false if a set of points all lie on the same plane they are called coplanar
Answers
Answer:
True
Step-by-step explanation:
Coplanar points: A group of points that lie in the same plane are coplanar. Any two or three points are always coplanar. Four or more points might or might not be coplanar. The left side of the above figure shows coplanar points A, B, C, and D.
Hope this helps
{x - 2y + 4z = 4 -5x + 9y - 22z = -16 -2x + 3y - 10z = k In order for the system of equations above to be a consistent system, k must be equal to
Answers
In order for the system of equations to be a consistent system, the value of k must be equal to -4.
To determine the value of k that makes the system of equations consistent, we can use the method of elimination or substitution. Let's use the method of elimination.
First, we can multiply the first equation by 5, the second equation by -1, and the third equation by 2 to make the coefficients of x in the three equations cancel each other out when added together.
The modified system of equations becomes:
5x - 10y + 20z = 20
5x - 9y + 22z = 16
-4x + 6y - 20z = 2k
Now, let's subtract the first equation from the second equation:
(5x - 9y + 22z) - (5x - 10y + 20z) = 16 - 20
y + 2z = -4
Next, let's add this equation to the third equation:
(-4x + 6y - 20z) + (y + 2z) = 2k - 4
-4x + 7y - 18z = 2k - 4
For the system of equations to be consistent, there must be no contradictions or inconsistencies. This means that the equations must be linearly dependent, and the last equation must be a multiple of the second equation.
Comparing the last equation (-4x + 7y - 18z = 2k - 4) with the second equation (y + 2z = -4), we can see that the two equations will be dependent and consistent if 2k - 4 is equal to 0.
2k - 4 = 0
2k = 4
k = 2
Therefore, in order for the system of equations to be a consistent system, the value of k must be equal to -4.
To learn more about elimination click here, brainly.com/question/29807794
#SPJ11
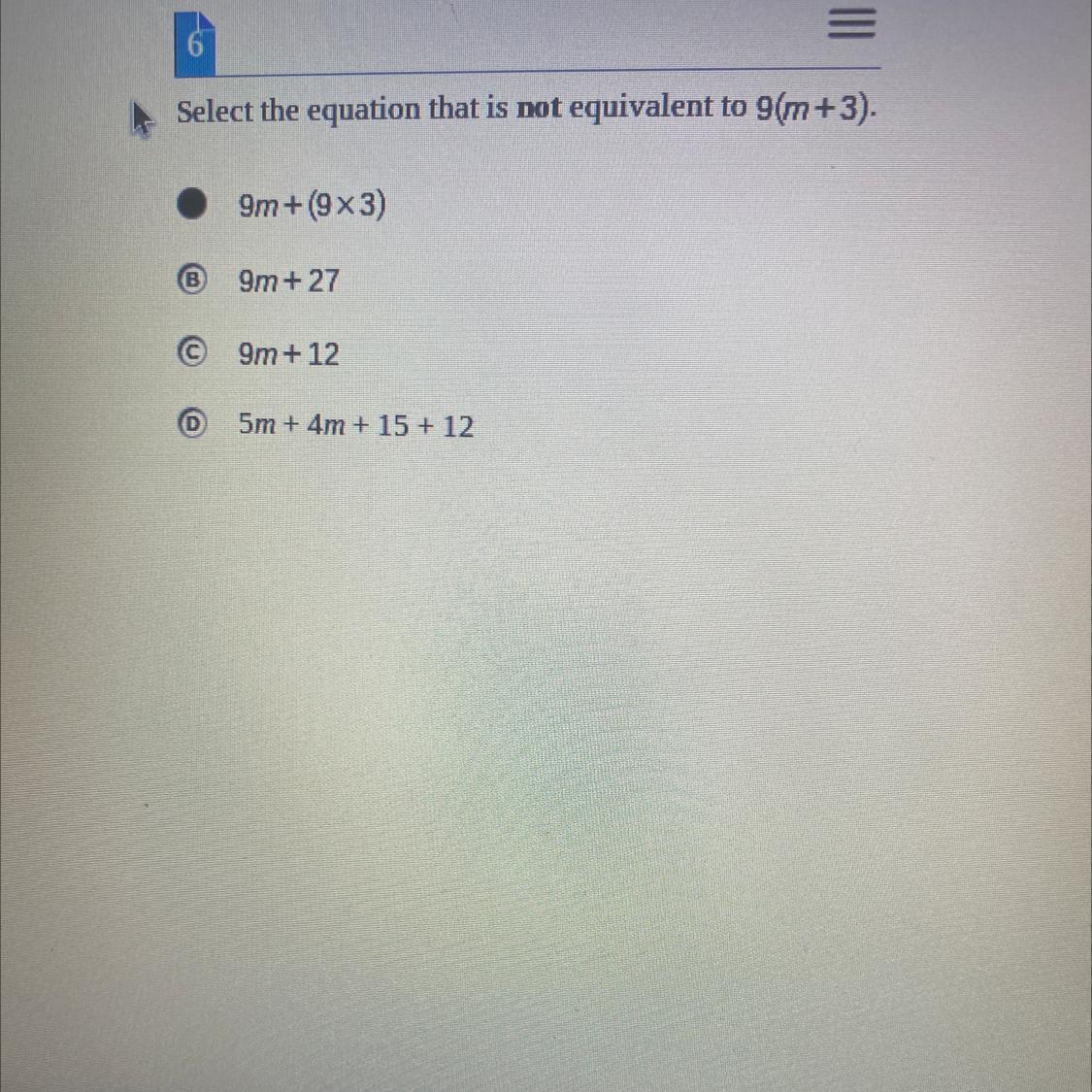
Pleaseee helppp
Select the equation that is not equivalent to 9(m+3).
9m +(9x3)
(В
9m +27
C 9m + 12
D
5m + 4m + 15 + 12
Answers
Answer:
C
Step-by-step explanation:
all the options can give 9m+27 except C; 9m+12
Multiply and rewrite as a trinomi please help fast

Answers
Answer:
x² - 2x - 15
This is the third answer choice
Step-by-step explanation:
(x + 3)(x - 5) can be multiplied using the FOIL method: First, Last, Outer, Inner
First: x · x = x²
Outer: x(-5) = -5x
Inner: (3)(x) = 3x
Last: 3 (-5) = -15
Adding everything we get
x² - 2x - 15
This is the third answer choice
Answer:
C) x² - 2x -15Step-by-step explanation:
\(\tt (x+3)(x-5)\)
Use the FOIL method:-
\(\boxed{\tt \left(a+b\right)\left(c+d\right)=ac+ad+bc+bd}\)
\(\tt x^2-5x+3x-15\)
Combine like terms:-
\(\tt x^2+(-5x+3x)-15\)
Simplify:-
\(\tt x^2-2x-15\)
Therefore, C) x² - 2x -15 is our answer.
_____________________
Hope this helps!
Which expression is equivalent to root 180
Answers
Answer:
No expressions listed. Some possibilities are below.
Step-by-step explanation:
(180)^(1/2)
Since 180 = 5*36, we can wite 6*\(\sqrt{5\\}\)
.
What is (4x2-9X+1) -(5x2-x-7) written in standard form?
Answers
Answer:
(9-9x) - (3-x)
Step-by-step explanation:
(4x2 -9x +1) - (5x2 -x -7)
4x2+1= 9. 5x2-7= 3
(9-9x) - ( 3-x)
in euclidean geometry the sum of the angles in a triangle equals 180 degrees. is this also true in spherical geometry?
Answers
The statement is not true for spherical geometry. Because the sum of the angles in a triangle in spherical geometry is not equal to 180 degrees.
"Information available from the question"
In the question:
In Euclidean geometry the sum of the angles in a triangle equals 180 degrees.
We have to identify that this is true for spherical geometry also;
Now, According to the question:
In a Euclidean space, the sum of angles of a triangle equals the straight angle (180 degrees, π radians, two right angles, or a half-turn). A triangle has three angles, one at each vertex, bounded by a pair of adjacent sides.
The sum of the angles of a spherical triangle is not equal to 180°. A sphere is a curved surface, but locally the laws of the flat (planar) Euclidean geometry are good approximations. In a small triangle on the face of the earth, the sum of the angles is only slightly more than 180 degrees.
Learn more about Euclidean geometry at:
https://brainly.com/question/4637858
#SPJ4
please solve this
no links

Answers
Answer:
0.375
Step-by-step explanation:
2÷3 = 1.5
1.5÷4 = 0.375
(An Intermediate Agebra review exerdse) Use poivnomial fong division to perform the indicated division, Write the polynomiaf in the form \( p(x)=d(x) q(x)+r(x) \). \[ \left(5 x^{4}-3 x^{3}+2 x^{2}-9\r
Answers
The quotient is \(q(x) = 5x^3 + 7x^2 + 16x + 32\) and the remainder is \(r(x) = 55\). To perform polynomial long division for the given polynomial \[5x^4 - 3x^3 + 2x^2 - 9\] and the divisor, let's assume it to be \[d(x) = x - 2.\]
First, we start by dividing the highest-degree term of the dividend (5x^4) by the highest-degree term of the divisor (x). This gives us a quotient term of 5x^3.
Next, we multiply the entire divisor (x - 2) by the quotient term (5x^3), which gives us 5x^4 - 10x^3. We then subtract this from the original dividend, like a regular subtraction.
\[5x^4 - 3x^3 + 2x^2 - 9 - (5x^4 - 10x^3) = 7x^3 + 2x^2 - 9.\]
We bring down the next term from the dividend, which is 0x^2 (since there is no x^2 term in the remaining dividend). Now, we repeat the process by dividing the highest-degree term of the new dividend (7x^3) by the highest-degree term of the divisor (x). This gives us a new quotient term of 7x^2.
Multiplying the entire divisor (x - 2) by the new quotient term (7x^2) gives us 7x^3 - 14x^2. Subtracting this from the new dividend gives us:
\[7x^3 + 2x^2 - 9 - (7x^3 - 14x^2) = 16x^2 - 9.\]
Again, we bring down the next term from the dividend, which is 0x (since there is no x term in the remaining dividend). We divide the highest-degree term of the new dividend (16x^2) by the highest-degree term of the divisor (x), resulting in a quotient term of 16x.
Multiplying the entire divisor (x - 2) by the new quotient term (16x) gives us 16x^2 - 32x. Subtracting this from the new dividend gives us:
\[16x^2 - 9 - (16x^2 - 32x) = 32x - 9.\]
Finally, we bring down the last term from the original dividend, which is -9. We divide the highest-degree term of the new dividend (32x) by the highest-degree term of the divisor (x), giving us a quotient term of 32.
Multiplying the entire divisor (x - 2) by the new quotient term (32) gives us 32x - 64. Subtracting this from the new dividend gives us:
\[32x - 9 - (32x - 64) = 55.\]
Now, since the degree of the new dividend (55) is less than the degree of the divisor (x - 2), we cannot continue the division further. Therefore, the final result of the polynomial long division is:
\[5x^4 - 3x^3 + 2x^2 - 9 = (x - 2)(5x^3 + 7x^2 + 16x + 32) + 55.\]
Thus, the quotient is \(q(x) = 5x^3 + 7x^2 + 16x + 32\) and the remainder is \(r(x) = 55\).
Learn more about polynomial here:
https://brainly.com/question/11536910
#SPJ11
01
3
✓5
Check
Unit price for the 2.24-pound bag:
$per pound
Unit price for the 3.12-pound bag: $ per pound
The better buy:
O The 2.24-pound bag
O The 3.12-pound bag
O Neither (They have the same unit price)
Answers
The better buy for the shrimp based on the information will be the A. 2.24 pound bag.
How to calculate the unit price?From the information, Josh paid $11.96 for a 2.24 -pound bag of shrimp at one store and the following week, he paid $17.24 for a 3.12 -pound bag at another store.
The unit price when Josh paid $11.96 for a 2.24 -pound bag of shrimp will be:
= $11.96 / 2.24
= $5.34
The unit price when he paid $17.24 for a 3.12 -pound bag at another store will be:
= $17.24 / 3.12
= $5 53
Therefore, A is cheaper.
Learn more about unit price on:
brainly.com/question/26959824
#SPJ1
Complete question
Josh paid $11.96 for a 2.24 -pound bag of shrimp at one store. The following week, he paid $17.24 for a 3.12 -pound bag at another store. Find the unit price for each bag. Then state which bag is the better buy based on the unit price. Round your answers to the nearest cent.
The number 686 can be expressed as a product of prime factors in the form p x qr. The value of p+q+r is _________. Work must be shown.
Answers
Answer:
p + q + r is 12.
Step-by-step explanation:
Prime factors of a number is the expression of the number in terms of the product of its factors that are prime numbers only.
The prime factor of 686 = 2 x 7 x 7 x 7. Which can be expressed in the form;
p × \(q^{r}\) as 2 × \(7^{3}\).
So that, p = 2, q = 7 and r = 3.
p + q + r = 2 + 7 + 3
= 12
Therefore, the sum of p, q, and r is 12.
give the laplace transform of f(x) = -2x-4 0<=x and x<2
Answers
The laplace transform of f(x) = -2x-4 is L{-2x-4} = (8 - 2s - 4e^(-2s))/s
The Laplace transform of f(x) = -2x-4 for 0<=x and x<2 can be found using the formula:
finding Laplace transform:L{f(x)} = ∫[0,∞) e^(-sx) f(x) dx
Substituting the given function and limits, we get:
L{-2x-4} = ∫[0,2) e^(-sx) (-2x-4) dx
= -2 ∫[0,2) x e^(-sx) dx - 4 ∫[0,2) e^(-sx) dx
Using integration by parts, we can evaluate the first integral as:
-2 ∫[0,2) x e^(-sx) dx = [-2xe^(-sx)] [0,2) + 2 ∫[0,2) e^(-sx) dx
= 2 (1 - e^(-2s))
Evaluating the second integral is straightforward:
-4 ∫[0,2) e^(-sx) dx = -4 [e^(-sx)/(-s)] [0,2)
= 4 (e^(-2s) - 1)/s
Therefore, the Laplace transform of f(x) = -2x-4 for 0<=x and x<2 is:
L{-2x-4} = 2 (1 - e^(-2s)) + 4 (e^(-2s) - 1)/s
Simplifying this expression, we get:
L{-2x-4} = (8 - 2s - 4e^(-2s))/s
To know more about Laplace transform:
https://brainly.com/question/31041670
#SPJ11
Find the sum of the series. [infinity] 5(−1)nπ2n + 1 32n + 1(2n + 1)! n = 0
Answers
The sum of the series is 1/16. The given series is: ∑ [infinity] 5(−1)nπ2n + 1 / 32n + 1(2n + 1)!
To find the sum of the series, we can use the ratio test to check the convergence of the series. First, let's take the ratio of the (n+1)th term to the nth term: | a(n+1) / a(n) | = 5π2 / 32(2n + 3)(2n + 2)(2n + 1)
As n approaches infinity, the denominator of the ratio tends to infinity, making the ratio go to zero. Therefore, by the ratio test, the series converges.
Now, we need to find the sum of the series. To do this, we can use the formula for the sum of an infinite series: S = lim [n → ∞] Sn, where Sn is the nth partial sum of the series.
Using partial fractions, we can write the series as: 5π2 / 32n + 1 (2n + 1)! = 1 / 64 [ 1 / (n!) - 1 / (2n + 1)! ] - 5π2 / 32(2n + 3)(2n + 2)(2n + 1)
Substituting this expression into Sn and simplifying, we get: Sn = (1 - cos(π/4n+1)) / 32
Taking the limit as n approaches infinity, we get: S = lim [n → ∞] Sn = 1 / 16 Therefore, the sum of the series is 1/16.
To know more about ratio test, refer here:
https://brainly.com/question/15586862#
#SPJ11
Feliks joins a local recreation center to play basketball the reception charges $20 annual fee plus additional $15 per month for the usage of the basketball courts Feliks prepays by writing a check for 3185 for how many months did he prepays for
Answers
Answer:
211 months
Step-by-step explanation:
Feliks joins a local recreation center to play basketball the reception charges $20 annual fee plus additional $15 per month for the usage of the basketball courts Feliks prepays by writing a check for 3185 for how many months did he prepays for
Let the number of months that he prepays for be represented by m
Hence, we have the equation
$20 + $15 × m = $3185
Hence:
20 + 15m = 3185
Collect like terms
15m = 3185 - 20
15m = 3165
m = 3165/15
m = 211 months
When you submit this form, the owner will see your name and email address.
1
Problem 1.
The force system shown is to be replaced with an equivalent system consisting of a horizontal force applied at b and a vertical force applied to the horizontal leg.
1.1. What is the magnitude of the vertical force, in Newton, applied to the horizontal leg? (rounded-off to the nearest whole number; do not write the unit)
Answers
The magnitude of the vertical force applied to the horizontal leg in the equivalent force system.
To determine the magnitude of the vertical force applied to the horizontal leg, we need to find the vertical component of the given force system. Looking at the diagram, we observe that the force system consists of a vertical force at point A and a horizontal force at point B. We can use trigonometry to find the vertical component of the force at point A.
Let's denote the magnitude of the force at point A as F_A and the angle it makes with the horizontal leg as θ. The vertical component of the force can be calculated using the formula: Vertical component = F_A * sin(θ).
Since the vertical component of the force should be equal to the force we are trying to find, we can set up the equation: Vertical component = F_vertical.
Now, we can substitute the given values into the equation and solve for F_vertical. Once we have the value, we can round it off to the nearest whole number, as instructed.
Please note that without specific values or angles provided in the problem statement or accompanying diagram, it is not possible to provide a precise numerical answer.
Learn more about angles here:
https://brainly.com/question/31818999
#SPJ11
if f(x)=6x^2-4 and g(x)=2x+2 find (f-g)(x)
Answers
Answer: \((f-g)(x)=6x^2-2x-6\)
Step-by-step explanation:
\(f(x)=6x^2-4\\g(x)=2x+2\\(f-g)(x)=\)
Take each function and subtract them.
\((f-g)(x)=(6x^2-4)-(2x+2)\)
The trick here is that the negative sign changes all of the signs inside the parentheses.
\((f-g)(x)=6x^2-4-2x-2\)
Combine like terms;
\((f-g)(x)=6x^2-2x-6\)
I am having difficulty solving derivatives. I was wondering if you could explain the product and quotient rule with examples? Thank you in advance!
Answers
Given:
Product and quotient rule.
Required:
Explain the product and quotient rule with examples.
Explanation:
Product rule:
If two functions are in the multiple forms then the derivative of two functions is given by the formula:
\(\frac{d}{dx}(u.v)=v\frac{d}{dx}u+u\frac{d}{dx}v\)where u = first function and v = second function.
Example
\(\begin{gathered} \frac{d}{dx}(x.sinx)=sinx.\frac{d}{dx}(x)+x\frac{d}{dx}(sinx) \\ \frac{d}{dx}(x.sinx)=sinx.(1)+x.(cosx) \\ \frac{d}{dx}(x.sinx)=sinx+xcosx \end{gathered}\)Quotient Rule:
If two functions are given in the quotient form or division form then the derivative of these functions using the quotient rule is given as:
\(\frac{d}{dx}(\frac{u}{v})=\frac{v\frac{d}{dx}u-u\frac{d}{dx}v}{v^2}\)Example:
\(\begin{gathered} \frac{d}{dx}(\frac{sinx}{x})=\frac{x\frac{d}{dx}sinx-sinx\frac{d}{dx}x}{x^2} \\ \frac{d}{dx}(\frac{sinx}{x})=\frac{x(cosx)-sinx(1)}{x^2} \\ \frac{d}{dx}(\frac{sinx}{x})=\frac{xcosx-sinx}{x^2} \end{gathered}\)Final Answer:
As explained in the explanation part.
a bank wishes to estimate the mean credit card balance owed by its customers. the population standard deviation is estimated to be $300. if a 98% confidence interval is used and an margin of error of $89 is desired, how many customers should be sampled? group of answer choices 429 19 162 62
Answers
The bank should sample 429 customers.
To determine the number of customers that should be sampled, we need to use the formula for sample size calculation in estimating a population mean. The formula is given by:
n = (Z * σ / E)^2
Where:
n = sample size
Z = corresponding to the desired level of confidence (98% confidence corresponds to a z-score of approximately 2.33)
σ = population standard deviation
E = desired margin of error
Plugging in the given values, we have:
n = (2.33 * 300 / 89)^2
n ≈ 429
Therefore, the bank should sample approximately 429 customers.
Learn more about z-score here:
brainly.com/question/31871890
#SPJ11
Oliver estimates the weight of his cat to be 16 pounds. The actual weight of his cat is 14.25 pounds. What is the percent error of Olver's estimate? Round the percent to the nearest tenth if necessary.
Answers
ANSWER
The percent error is 10.9 %
EXPLANATION
The percent error is:
\(\text{ \% error}=\frac{|approx-exact|}{exact}\times100\)In this problem, the approximate value is 16 and the exact value is 14.25:
\(\begin{gathered} \text{ \% error}=\frac{|14.25-16|}{16}\times100 \\ \text{ \% error}=\frac{1.75}{16}\times100 \\ \text{ \% error}=0.109375\times100 \\ \text{ \% error}=10.9375\approx10.9\text{ \%} \end{gathered}\)Answer:
10.9%
Step-by-step explanation:
14.25/16 = 0.890625
0.890625 * 100 = 89.0625
1 - 89.0625 = 10.9375%