Elyse wants to buy a new softball glove that costs $45. She has $15 and plans to save 5 each week. How many weeks will it take her to save the money?
Answers
Answer:
6 weeks :)
Step-by-step explanation:
it will take her 6 weeks
45-15 is 30.
30/5 is 6
Answer:
It will take her 6 weeks.
Step-by-step explanation:
$45-$15=$30
$30 ÷ $5 = 6
Related Questions
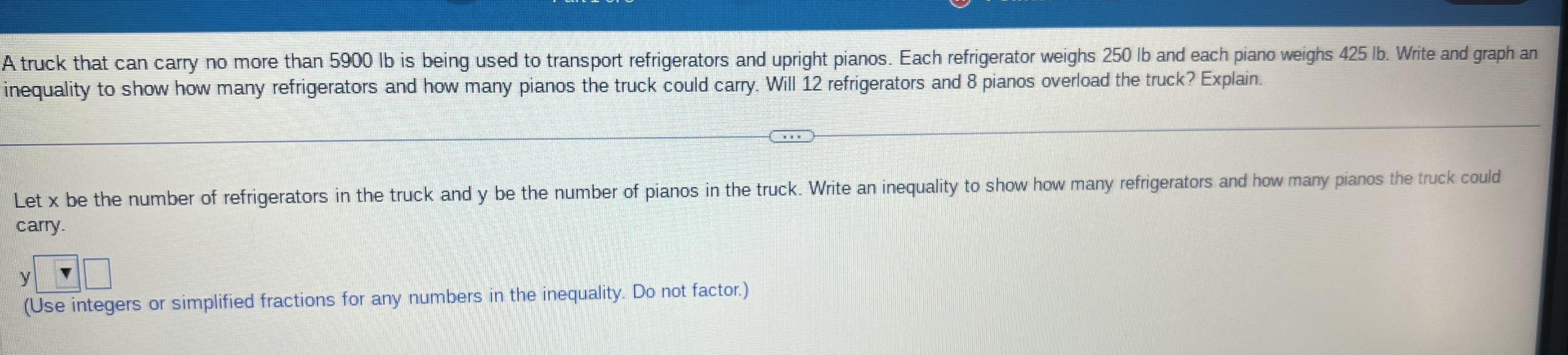
i need help immediately, im giving out twenty point for help
Answers
Answer:
250x +425y ≤ 5900the truck will be overloadedStep-by-step explanation:
You want an inequality relating the number of 250 lb refrigerators (x) and the number of 425 lb pianos (y) a truck with a 5900 lb load limit can carry. And you want to know if 12 refrigerators and 8 pianos will overload the truck.
LoadThe weight of x refrigerators will be 250x. The weight of y pianos will be 425y. Then the restriction on the total weight is ...
250x +425y ≤ 5900 . . . . . . the load limit of the truck
OverloadThe weight of 12 refrigerators and 8 pianos will be ...
250·12 +425·8 = 3000 +3400 = 6400 . . . . pounds
This weight will overload the truck.
__
Additional comment
The graph shows the point (12, 8) is not in the solution space of the inequality. Hence the truck will be overloaded with that load.
<95141404393>

1. TEMPERATURE Suppose the temperature
outside is dropping 3 degrees each
hour. How much will the temperature
drop in 8 hour?
Answers
3x8=24
Every year in delaware there is a contest where people create cannons and catapults designed to launch pumpkins as far in the air as possible. the equation y=10+95x-16x^2 can be used to represent the height, y, of a launched pumpkin, where x is the time in seconds that the pumpkin has been in the air. what is the maximum height that the pumpkin reaches?
Answers
Therefore , the solution to the given problem of equation comes out tot be maximum height of 151 feets.
Equation: What is it?An equation is a statement in mathematical language that two variables or mathematical expressions are equal. Observe how the left and right weights are equal to each other. We use the equal sign to denote equivalence between two integers or mathematical equations. For example, the formula for the aforementioned situation is 5 kg Plus 2 kg = 4 kg + 3 kg.
Here,
The maximum height of the pumpkin is 151 feet, according to notions of quadratic functions.
After 6.04 seconds, the pumpkin lands.
Following x seconds, the height of the pumpkin is predicted by:
y = -16\(x^{2}\) + 95x +10
It has coefficients and is a quadratic equation. A is -16, B is 95, and C is 10
The y-value of the vertex, which is determined by:
Y(max) = -Δ / 4a = -\(b^{2}\) - 4ac /4a
Hence:
=> Δ = \(b^{2}\) - 4ac
=> Δ = (95*95) - 4(-16)(10)
=> Δ = 9665
=> Y(max) = -Δ / 4a
=> Y(max) = -9665 / 4(-16)
=> Y(max) =151
Therefore , the solution to the given problem of equation comes out tot be maximum height of 151 feets.
To know more about equation , visit
brainly.com/question/10413253
#SPJ4
In finance, we need to do partial observations of data and estimate the data generating process (DGP) -- for example, log-normal returns. Sometimes, we can observe only the data points of a certain process, but we don't know what is the function generating the process. Consider the following graph is a plot of the f ′
(x), of a function f(x) given. What is the underlaying function ( f(x −
i)) that is the generator of the observed points in the plot f ′
(x −
i), for points x −
1=−1,x −
2=−0.9,…,x −
n=1?
Answers
The underlying function f(x - i) that generates the observed points f'(x - i) in the plot can be determined by integrating the observed points. By integrating f'(x - i), we can obtain f(x - i) up to a constant of integration.
The constant of integration can be determined by incorporating additional information or constraints related to the problem or by considering the behavior of the function at a specific point.
To find the underlying function f(x - i) that generates the observed points f'(x - i), we need to integrate the observed points.
Integration is the reverse process of differentiation, so by integrating f'(x - i), we can recover f(x - i) up to a constant of integration.
The constant of integration arises because integration does not provide a unique solution.
The constant represents an arbitrary additive term that can vary depending on the specific problem or additional constraints.
To determine the constant of integration, we may need additional information or consider specific conditions related to the problem.
It is also important to note that the accuracy of estimating the underlying function f(x - i) depends on the quality and quantity of the observed data points f'(x - i). More data points and precise measurements can lead to a better estimation of the underlying function.
Additionally, the behavior of the function at a specific point can provide valuable insights for determining the constant of integration and refining the estimation of the underlying function.
To learn more about integration visit:
brainly.com/question/31954835
#SPJ11
Which number lines have points that represent additive inverses? Check all that apply.
Answers
Answer:
b and d on edge
Step-by-step explanation:
bc it is
Answer:
false
true
false
true
Step-by-step explanation:
hope it helps :)
If an undamped spring-mass system with a mass that weighs 24 lb and a spring constant 4 lb/in is suddenly set in motion at t=0 by an external force of 108 cos(4t) lb, determine the position of the mass at any time. Assume that g=32 ft/s2. solve for u in feet.
u(t)=
Answers
The position of the mass in the undamped spring-mass system can be represented by the equation u(t) = (A cos(ωt) + B sin(ωt)) / k. Therefore, position of the mass at any time t in feet is given by u(t) = 4.5 cos(4t).
In this case, the external force acting on the system is 108 cos(4t) lb. To determine the position of the mass, we need to solve the differential equation that represents the motion of the system.
Using Newton's second law, F = ma, and considering that the mass m = 24 lb, the equation becomes:
24 * d^2u/dt^2 = 108 cos(4t)
Simplifying, we have:
d^2u/dt^2 = 4.5 cos(4t)
This is a second-order linear homogeneous differential equation with a constant coefficient. The solution to this equation will be a linear combination of the homogeneous and particular solutions.
The homogeneous solution, representing the free oscillation of the system, is u_h(t) = C1 cos(2t) + C2 sin(2t).
The particular solution, representing the forced motion caused by the external force, can be assumed in the form u_p(t) = A cos(4t) + B sin(4t).
By substituting u_p(t) into the differential equation, we can determine the values of A and B.
Solving the differential equation for the particular solution, we find:
A = 18 and B = 0
The complete solution for the position of the mass in feet is:
u(t) = (18 cos(4t)) / 4
Simplifying further, we get:
u(t) = 4.5 cos(4t)
Therefore, the position of the mass at any time t in feet is given by u(t) = 4.5 cos(4t).
To learn more about mass click here, brainly.com/question/30940568
#SPJ11
7.33 In one area along the interstate, the number of dropped wireless phone connections per call follows a Poisson distribution. From four calls, the number of dropped connections is 2 0 3 1 (a) Find the maximum likelihood estimate of lambda. (b) Obtain the maximum likelihood estimate that the next two calls will be completed without any ac- cidental drops.
Answers
(A) The maximum likelihood estimate of lambda is 1.5.
(B) The maximum likelihood estimate that the next two calls will be completed without any accidental drops is e^(-3).
To find the maximum likelihood estimate of lambda in a Poisson distribution representing the number of dropped wireless phone connections per call, we can analyze the given data. From four calls with the number of dropped connections as 2, 0, 3, and 1, we can determine the lambda value that maximizes the likelihood of observing these specific outcomes. Using the maximum likelihood estimation, we can also estimate the likelihood of the next two calls being completed without any accidental drops.
(a) To find the maximum likelihood estimate of lambda, we need to determine the parameter that maximizes the likelihood of observing the given data. In a Poisson distribution, the probability mass function is given by P(X = x) = (e^(-lambda) * lambdaˣ) / x!, where X is the number of dropped connections and lambda is the average number of dropped connections per call.
Given the data: 2, 0, 3, 1, we calculate the likelihood function L(lambda) as the product of the individual probabilities:
L(lambda) = P(X = 2) * P(X = 0) * P(X = 3) * P(X = 1)
To find the maximum likelihood estimate, we differentiate the logarithm of the likelihood function with respect to lambda, set it equal to zero, and solve for lambda. However, for simplicity, we can directly observe that the likelihood is maximized when lambda is the average of the given data points:
lambda = (2 + 0 + 3 + 1) / 4
lambda = 6 / 4
lambda = 1.5
Therefore, the maximum likelihood estimate of lambda is 1.5.
(b) To estimate the likelihood of the next two calls being completed without any accidental drops, we can use the maximum likelihood estimate of lambda obtained in part (a). In a Poisson distribution, the probability of observing zero dropped connections in a call is given by P(X = 0) = (e^(-lambda) * lambda^0) / 0!, which simplifies to e^(-lambda).
Using lambda = 1.5, we can calculate the probability of zero dropped connections in a call:
P(X = 0) = e^(-1.5)
To estimate the likelihood of two consecutive calls without any drops, we multiply the individual probabilities:
P(X = 0 in call 1 and call 2) = P(X = 0) * P(X = 0) = (e^(-1.5))^2 = e^(-3)
Therefore, the maximum likelihood estimate that the next two calls will be completed without any accidental drops is e^(-3).
Learn more about Maximum:
brainly.com/question/29130692
#SPJ11
Find the value of x
3^{x + 1} - 3^x = 2
Answers
Answer:
\(\boxed{x = 0}\)
Step-by-step explanation:
\(3^{x + 1} - 3^x = 2\)
\(3.3^x - 3^x = 2\)
\((3 - 1)3^x = 2\)
\(2.3^x = 2\)
\(3^x = \frac{2}{2}\)
\(3^x = 1\)
\(3^x = 3^0\)
\(x = 0\)
the value of x is zero
learn more about eksponen to solve this answer
Tegan is checking her tax bill for the last year
the tax rates were as follows:
•no tax on the first £11000 of earnings
•earnings in excess of £11000 and up to £43000 taxed at a rate of 20%
•earnings in excess of £43000 and up to £150000 taxed at the rate of 40%
last year Tegan earned £48300 before tax
how much did she pay in total?
Answers
Multiplication is the process of multiplying. The total tax of Tegan's earnings will be £8,520(£6,400+£1,200).
What is multiplication?Multiplication is the process of multiplying, therefore, adding a number to itself for the number of times stated. For example, 3 × 4 means 3 is added to itself 4 times, and vice versa for the other number.
Since there is no tax for the first £11,000, therefore, the earnings upto £11,000 will be tax-free.
The amount of tax for the income of £11,000 to £43,000, will be,
20% of (£11,000 to £43,000)
= 20% × (£43,000 - £11,000)
= £6,400
The amount of tax for the income of £11,000 to £150,000, will be,
40% of (£43,000 to £48,300)
= 40% × (£5,300)
= £2,120
Hence, the total tax of Tegan's earnings will be £8,520(£6,400+£1,200).
Learn more about Multiplication:
https://brainly.com/question/14059007
#SPJ1
Answer:
£8520
Step-by-step explanation:
A recipe calls for 1/3/4 cups of sugar. The recipe requires 3/4 cup more flour than sugar and 1/2 cup less butter than sugar.
Answers
Answer:
what is the question??
1. (a) Explain how to find the anti-derivative of f(3) = 12 r sin (23-2). (b) Explain how to evaluate the following definite integral: sin 5 3 dr.
Answers
The antiderivative of f(x) is 3 ∫ \(x^2\) cos(\(x^3\)-2) dx. The definite integral \(\int_{\frac{9\pi}{20}}^{\frac{24\pi}{5}} \sin\left(\frac{5x}{3}\right) dx\) is evaluated as (3 + 3√2)/10.
To find the antiderivative of the function f(x) = 12\(x^2\) sin(\(x^3\)-2), we can follow the general rules of integration.
First, we need to identify the function that, when differentiated, gives us f(x).
In this case, the derivative of sin(\(x^3\)-2) is cos(\(x^3\)-2), but we also have to account for the chain rule due to the \(x^3\)-2 inside the sine function.
Thus, the derivative of \(x^3\)-2 is 3\(x^2\), so we multiply the integrand by 3\(x^2\).
Therefore, the antiderivative of f(x) is:
F(x) = ∫ 12\(x^2\) sin(\(x^3\)-2) dx = 3 ∫ \(x^2\) cos(\(x^3\)-2) dx
To evaluate the definite integral ∫ sin(5x/3) dx from 9π/20 to 24π/5, we need to find the antiderivative of sin(5x/3) and then apply the fundamental theorem of calculus.
The antiderivative of sin(5x/3) is -3/5 cos(5x/3).
Using the fundamental theorem of calculus, we can evaluate the definite integral as follows:
∫ sin(5x/3) dx = -3/5 cos(5x/3) + C
To find the value of the definite integral from 9π/20 to 24π/5, we subtract the value of the antiderivative at the lower limit from the value at the upper limit:
\(\int_{\frac{9\pi}{20}}^{\frac{24\pi}{5}} \sin\left(\frac{5x}{3}\right) dx\) = [-3/5 cos(5(24π/5)/3)] - [-3/5 cos(5(9π/20)/3)]
Simplifying the angles within the cosine function:
= [-3/5 cos(8π/3)] - [-3/5 cos(3π/4)]
Now, we can evaluate the cosine values:
= [-3/5 (-1/2)] - [-3/5 (-√2/2)]
= 3/10 + 3√2/10
Combining the terms with a common denominator:
= (3 + 3√2)/10
So, the value of the definite integral ∫(9π/20 to 24π/5) sin(5x/3) dx is (3 + 3√2)/10.
Learn more about definite integral here:
https://brainly.com/question/30760284
#SPJ11
The complete question is:
1.(a) Explain how to find the anti-derivative of f(x) = 12 \(x^2\) sin (\(x^3\)-2).
(b) Explain how to evaluate the following definite integral: \(\int_{\frac{9\pi}{20}}^{\frac{24\pi}{5}} \sin\left(\frac{5x}{3}\right) dx\)
Find the area of the figure. (Sides meet at right angles.) 2m 4m 3m 4m 2m 4m 4m
Answers
To find the area of the figure, we need to divide it into rectangles and add up their areas. We can see that the figure is made up of three rectangles:
- One rectangle with sides 2m and 4m, giving an area of 8m².
- One rectangle with sides 3m and 4m, giving an area of 12m².
- One rectangle with sides 2m and 4m, giving an area of 8m².
Adding up these areas, we get:
8m² + 12m² + 8m² = 28m²
Therefore, the area of the figure is 28 square meters.
Note that the fact that the sides meet at right angles is important, because it allows us to divide the figure into rectangles and calculate their areas easily. If the sides did not meet at right angles, the figure might not be able to be divided into rectangles, and we would need a different method to find its area.
To know more about angles visit :-
https://brainly.com/question/25716982
#SPJ11
Write three more equations for 1ị that are all true and all different. Use only fractions with a denominator of 3 in your equations. 1 2/3 =1 2/3 =1 2/3 =
Answers
That we added a real number (2/3) and subtracted a real number (3), but the imaginary part of the result is still (5/3)i.
First, let me clarify what 1ị represents. In mathematics, the imaginary unit i is defined as the square root of -1. Therefore, 1ị means 1 times the imaginary unit i.
To write three more equations for 1ị that are all true and all different, we can use the fact that i satisfies the equation i^2 = -1. We can also use the fact that any multiple of i, such as 2i, 3i, and so on, is also an imaginary number. Finally, we can use the fact that adding or subtracting real numbers to or from an imaginary number does not affect the imaginary part of the number.
Here are three possible equations for 1ị:
(2 + 1/3)i = 1ị + 2i
Explanation: We can add 2 times the imaginary unit i to 1 times the imaginary unit i to get 3 times the imaginary unit i, which is equal to (2 + 1/3) times the imaginary unit i.
(-1/3)i = 1ị - 4/3i
Explanation: We can subtract 4/3 times the imaginary unit i from 1 times the imaginary unit i to get -1/3 times the imaginary unit i.
(5/3)i = 1ị + 2/3 + 3i - 3
Explanation: We can add 2/3 and 3i - 3 to 1 times the imaginary unit i to get (5/3) times the imaginary unit i. Notice that we added a real number (2/3) and subtracted a real number (3), but the imaginary part of the result is still (5/3)i.
To learn more about subtracted visit:
https://brainly.com/question/2346316
#SPJ11
3/12 simplified version
Answers
Answer:
1/4
Step-by-step explanation:
divide numerator and denominator by 3
4. There are 50 pupils in a class. Four-fifths of the class are boys
How many are boys?
Answers
Answer:
40
Step-by-step explanation:
50 x (4/5) = 50 x 4 =200/5=40
Answer:
aba mag solve kayo mag puro tanong samin
Find The Total Differentials Of The Following Utility Functions. A. U(X,Y)=Xαyβ B. U(X,Y)=X2+Y3+Xy
Answers
A. The total differential of the utility function U(X,Y) = X^αY^β is dU = αX^(α-1)Y^β dX + βX^αY^(β-1) dY.
B. The total differential of the utility function U(X, Y) = X^2 + Y^3 + XY is dU = (2X + Y) dX + (3Y^2 + X) dY.
A. The total differential of a function represents the small change in the function caused by infinitesimally small changes in its variables. In this case, we are given the utility function U(X, Y) = X^αY^β, where α and β are constants.
To find the total differential, we differentiate the utility function partially with respect to X and Y, and multiply the derivatives by the differentials dX and dY, respectively.
For the partial derivative with respect to X, we treat Y as a constant and differentiate X^α with respect to X, which gives αX^(α-1). We then multiply it by the differential dX.
Similarly, for the partial derivative with respect to Y, we treat X as a constant and differentiate Y^β with respect to Y, resulting in βY^(β-1). We then multiply it by the differential dY.
Adding these two terms together, we obtain the total differential of the utility function:
dU = αX^(α-1)Y^β dX + βX^αY^(β-1) dY.
This expression represents how a small change in X (dX) and a small change in Y (dY) affect the utility U(X, Y).
B. To find the total differential of the utility function U(X, Y) = X^2 + Y^3 + XY, we differentiate each term of the function with respect to X and Y, and multiply the derivatives by the differentials dX and dY, respectively.
For the first term, X^2, we differentiate it with respect to X, resulting in 2X, which is then multiplied by dX. For the second term, Y^3, we differentiate it with respect to Y, resulting in 3Y^2, which is multiplied by dY. Finally, for the third term, XY, we differentiate it with respect to X and Y separately, resulting in X (multiplied by dY) and Y (multiplied by dX).
Adding these three terms together, we obtain the total differential of the utility function:
dU = (2X + Y) dX + (3Y^2 + X) dY.
This expression represents how a small change in X (dX) and a small change in Y (dY) affect the utility U(X, Y).
Learn more about derivatives here: brainly.com/question/29144258
#SPJ11
Question
- which transformations, when performed together would carry graph A onto graph B? Choose all that apply.
Options
A- translation of 4 units up
B - verticals stretch with a scale factor of 2
C - vertical compression with a scale factor if 1/2
D - reflection over the x axis

Answers
The correct answer exists
A- translation of 4 units up
B - verticals stretch with a scale factor of 2
C - vertical compression with a scale factor if 1/2.
What is meant by graph transformation?A graph transformation is a method for altering an existing graph or graphed equation to create a different version of the graph that follows. The modification of algebraic equations is a typical form of algebraic issue.
A transformation is a method for changing the two-dimensional position of a polygon or other object on a plane or coordinate system. Two-dimensional figures can move across a plane or coordinate system via mathematical transformations. The shape in two dimensions before any alteration is known as a preimage or inverse image.
Translation, rotation, reflection, and dilation are the four basic forms of transformations. A rotation about any point, a reflection over any line, and a translation along any vector are all possible according to the description of the transformation. These are rigid transformations in which the image is identical to its starting point.
Therefore, the correct answer exists
A- translation of 4 units up
B - verticals stretch with a scale factor of 2
C - vertical compression with a scale factor if 1/2.
To learn more about graph transformation refer to:
brainly.com/question/4025726
#SPJ1
Calculate the 95 confidence interval for the true population mean based on a sample with =225, =8.5, and =45.
Answers
The 95% confidence interval for the true population mean, based on a sample with a sample size (n) of 225, a sample mean (X) of 8.5, and a sample standard deviation (σ) of 45, is (2.62, 14.38).
To calculate the confidence interval, we can use the formula:
Confidence interval = X ± Z * (σ/√n)
where X is the sample mean, Z is the critical value for the desired level of confidence (in this case, 95%), σ is the sample standard deviation, and n is the sample size.
The critical value Z can be obtained from a standard normal distribution table or calculated using statistical software. For a 95% confidence level, the Z-value is approximately 1.96.
Plugging in the values into the formula, we get:
Confidence interval = 8.5 ± 1.96 * (45/√225)
= 8.5 ± 1.96 * (45/15)
= 8.5 ± 1.96 * 3
Calculating the upper and lower bounds of the confidence interval:
Upper bound = 8.5 + 1.96 * 3
= 8.5 + 5.88
= 14.38
Lower bound = 8.5 - 1.96 * 3
= 8.5 - 5.88
= 2.62
Therefore, the 95% confidence interval for the true population mean is (2.62, 14.38).
Learn more about confidence intervals here:
brainly.com/question/32546207
#SPJ4
the 2 triangles are similar. if the perimeter of triangle abc is 28, find the value of x

Answers
so 10 + x - 4 + x - 1.5 = 35
4.5 + 2x = 35
2x = 30.5
x = 15.25
AC method factoring requires the polynomial to be
Answers
look at pic......................................

Answers
Answer:
I'm not sure tbh, sorry .
a) Calculate the scale factor from shape A to shape B.
b) Find the value of t.
Give each answer as an integer or as a fraction in its simplest form.
A
5 cm
15 cm
7cm
B
12 cm
4cm
t cm

Answers
The scale factor from A to B is 5 / 4.
The value of t in the diagram is 5.6 cm.
How to find scale factor?Scale factor is the ratio between corresponding measurements of an object and a representation of that object.
Therefore, let's find the scale factor from the shape A to the shape B as follows:
5 / 4 = 15 / 12
Therefore, the scale factor is 5 / 4.
Hence, let's find the value of t in the diagram as follows:
Therefore, using the proportionality,
7 / t = 5 / 4
cross multiply
28 = 5t
divide both sides by 5
t = 28 / 5
t = 5.6 cm
learn more on scale factor here: brainly.com/question/16609931
#SPJ1
Is the differential equation (cos x cos y + 4y)dx + (sin x sin y + 10y)dy = 0 exact? yes no
Answers
F(x,y) = y\(e^{xsiny + xy - sinx}\) + ∫sin y\(e^{xsiny + xy - sinx}\)dx is a solution to the original differential equation.
Here, we have,
This is a first-order nonlinear differential equation, which is not separable or linear. However, it is possible to use an integrating factor to solve it.
The first step is to rearrange the equation into the standard form:
(y cos x + sin y + y)dx + (sin x + x cos y + x)dy = 0
Next, we need to identify the coefficient functions of dx and dy, which are:
M(x,y) = y cos x + sin y + y
N(x,y) = sin x + x cos y + x
Now we can find the integrating factor, which is defined as a function u(x,y) that makes the equation exact. The integrating factor is given by:
u(x,y) = \(e^{(\int\,(N(x,y) - dM/dy) dy) }\)
where ∂M/∂y is the partial derivative of M with respect to y.
Evaluating this integral, we get:
u(x,y) = \(e^{xsiny + xy - sinx}\)
Multiplying both sides of the original equation by the integrating factor, we get:
(\(e^{xsiny + xy - sinx}\)) [y cos x + sin y + y])dx + (\(e^{xsiny + xy - sinx}\) [sin x + x cos y + x])dy = 0
This equation is exact, which means that there exists a function F(x,y) such that ∂F/∂x = M(x,y) and ∂F/∂y = N(x,y). We can find this function by integrating M with respect to x, while treating y as a constant, and then differentiating the result with respect to y:
F(x,y) = ∫(y cos x + sin y + y)\(e^{xsiny + xy - sinx}\)dx = y\(e^{xsiny + xy - sinx}\) + ∫sin y\(e^{xsiny + xy - sinx}\)dx
Now we can differentiate F with respect to y, while treating x as a constant, and compare the result with N:
∂F/∂y = x\(e^{xsiny + xy - sinx}\) + cos y\(e^{xsiny + xy - sinx}\) + \(e^{xsiny + xy - sinx}\)
= sin x + x cos y + x
Therefore, F(x,y) = y\(e^{xsiny + xy - sinx}\) + ∫sin y\(e^{xsiny + xy - sinx}\)dx is a solution to the original differential equation.
learn more about differential equation:
brainly.com/question/2030026
#SPJ1
complete question:
Solve (y cos x + sin y + y)dx + (sin x + x cos y + x)dy = .0
2 A bag contains three red counters, four green counters, two yellow counters and one white
counter. Two counters are drawn from the bag one after the other, without being replaced.
Calculate:
a P(two red counters)
b P(two green counters)
c P(two yellow counters)
d P(white and then red)
e P(white or yellow, in either order but not both)
f P(white or red, in either order but not both).
g What is the probability of drawing a white or yellow counter first and then any
colour second?
Answers
P (two red counters) = 1/15
P (two green counters) = 2/15
P (two yellow counters) = 1/145
P (white and then red) = 1/30
P (white or yellow, in either order but not both) = 3/10
P (white or red, in either order but not both) = 2/5
The probability of drawing a white or yellow counter first and then any
color second = 7/30
What is probability?It is the chance of an event to occur from a total number of outcomes.
The formula for probability is given as:
Probability = Number of required events / Total number of outcomes.
We have,
Number of red counters = 3
Number of green counters = 4
Number of yellow counters = 2
Number of white counters = 1
Total number of counters = 3 + 4 + 2 + 1 = 10
The probability of drawing 2 red counters.
= \(^3C_2\) / \(^{10}C_2\)
= 3 / 5 x 9
= 1/ 15
The probability of drawing 2 green counters.
= \(^4C_2\) / \(^{10}C_2\)
= 2 x 3 / 5 x 9
= 2/15
The probability of drawing 2 yellow counters.
= \(^2C_2\) / \(^{10}C_2\)
= 1 / 45
The probability of drawing one white and then one red counter.
= 1/10 x \(^3C_1\)/\(^{9}C_1\)
= 1/10 x 3/9
= 1/10 x 1/3
= 1/30
The probability of drawing one white or one yellow counter.
= 1/10 + 2/10
= 3/10
The probability of drawing one white or one red counter.
= 1/10 + 3/10
= 4/10
= 2/5
The probability of drawing one white or one yellow counter and one any counter.
= 3/10 x 7/9
= 7/30
Thus,
The required probabilities are given above.
Learn more about probability here:
https://brainly.com/question/14099682
#SPJ2
ASAPPPP!!! CAN U START FROM SECTION A TO SECTION B!!!!????
LISTEN HERE I NEED SOMEONE TO WORKOUT ALL OF THESE CUZ IF I DONT FINISH IT BY TOMZ I GET A DETENTION !!

Answers
Answer: I just did the ones that did not already have an answer
Section A:
7. 1.5 hours
9. 480 meters
10. 10 km
Section B:
1. 40 mph
2. 160 miles
3. 168 miles
4. 5.2 mph
5. 26.25 km/h
Find the explicit solution to the IVP,
⎝
⎛
No need
to state
domain
⎠
⎞
(No need to state the domain of your solution function.) 丈: y
′
=−1+(x+y)
2
,y(0)=1 5] (1) Find the solution (explicit) for the IVP : ⋆:y
′
=
x
2
2xy+y
2
,y(1)=1 and what is the (largest) possible domain for your solution? −(0,2)
Answers
The explicit solution to the first IVP is y = -x + x^3/3 + x^2/2 + C, and the second IVP does not have an explicit solution. The largest possible domain for the second IVP solution is (-∞,∞).
The explicit solution to the initial value problem (IVP) y' = -1 + (x+y)^2, y(0) = 1 is: y = -x + x^3/3 + x^2/2 + C
To find this solution, we integrate the differential equation with respect to x. After integration, we obtain an expression involving an arbitrary constant, C. This constant represents the freedom we have in choosing a specific solution curve.
Now, let's consider the IVP y' = x^2/(2xy+y^2), y(1) = 1. Unfortunately, this differential equation does not have an explicit solution. However, we can still find a solution numerically or graphically using methods like Euler's method or slope fields.
The largest possible domain for the solution to this IVP is the interval (-∞,∞), as there are no restrictions on x or y that would limit the domain of the solution function.
In summary, the explicit solution to the first IVP is y = -x + x^3/3 + x^2/2 + C, and the second IVP does not have an explicit solution. The largest possible domain for the second IVP solution is (-∞,∞).
Learn more about differential equation here:
https://brainly.com/question/33433874
#SPJ11
A plane flies 452 miles north and
then 767 miles west.
What is the direction of the
plane's resultant vector?
Hint: Draw a vector diagram.
Ө 0 = [ ? ]°
Round your answer to the nearest hundredth.
Answers
Answer:
149.49° (nearest hundredth)
Step-by-step explanation:
To calculate the direction of the plane's resultant vector, we can draw a vector diagram (see attachment).
The starting point of the plane is the origin (0, 0).Given the plane flies 452 miles north, draw a vector from the origin north along the y-axis and label it 452 miles.As the plane then flies 767 miles west, draw a vector from the terminal point of the previous vector in the west direction (to the left) and label it 767 miles.Since the two vectors form a right angle, we can use the tangent trigonometric ratio.
\(\boxed{\begin{minipage}{7 cm}\underline{Tangent trigonometric ratio} \\\\$ \tan x=\dfrac{O}{A}$\\\\where:\\ \phantom{ww}$\bullet$ $x$ is the angle. \\ \phantom{ww}$\bullet$ $\sf O$ is the side opposite the angle. \\\phantom{ww}$\bullet$ $\sf A$ is the side adjacent the angle.\\\end{minipage}}\)
The resultant vector is in quadrant II, since the plane is travelling north (positive y-direction) and then west (negative x-direction).
As the direction of a resultant vector is measured in an anticlockwise direction from the positive x-axis, we need to add 90° to the angle found using the tan ratio.
The angle between the y-axis and the resultant vector can be found using tan x = 767 / 452. Therefore, the expression for the direction of the resultant vector θ is:
\(\theta=90^{\circ}+\arctan \left(\dfrac{767}{452}\right)\)
\(\theta=90^{\circ}+59.4887724...^{\circ}\)
\(\theta=149.49^{\circ}\; \sf (nearest\;hundredth)\)
Therefore, the direction of the plane's resultant vector is approximately 149.49° (measured anticlockwise from the positive x-axis).
This can also be expressed as N 59.49° W.

Choose the function that represents the data in the table. Y = 3x + 2 y = 3x2 + 2 y = y = 3x + 2.
Answers
The function that represents the data in the table is 3x²+2. The correct answer is B.
The quadratic function is shown in the data table.
We must ascertain the function's equation.
The quadratic equation's generic form is
Let's replace the general form with the three coordinates (1,5, (2,14), and (3,29).
We therefore have;
a+b+c =5——— (1)
4a+2b+c= 14——— (2)
9a+3b+C =29------(3)
When (2) is subtracted from (1), we have;
9= 3a+b(4)
Subtracting (3) from (2) gives us;
15= 5a +b(5)
Subtracting (5) from (4) gives us;
6= 2a
3= a
As a result, the value of an is 3. When we replace this value in equation (4), we obtain;
3(3)+b= 9
b= 0
When a = 3 and b = 0 are substituted in equation (1), we obtain;
a+b+c =5
3+0+c=5
c=2
As a result, c has a value of 2.
As a result, when we substitute a = 3, b = 0, and c = 2 in the quadratic equation's general form y =ax²+bx+c, we obtain;
3x²+2
Consequently, the function that symbolizes the information in the table is 3x²+2
As a result, Option B is the right response.
Your question is incomplete but maybe your full question attached below
learn more about function at
https://brainly.com/question/29064184
#SPJ4

a paired samples test for the difference between two means can be used for segmentation purposes. true false
Answers
The statement "a paired samples test for the difference between two means can be used for segmentation purposes " is true
The given statement is
"A paired samples test for the difference between two means can be used for segmentation purposes"
The segmentation is the process of dividing the similar characteristics objects and group them together.
Here the a paired sample test for the difference between two mean is used for the segmentation process. It can be used for the segmentation purpose because A paired samples test for the difference between two means are samples in which natural or matched couplings occur
Therefore, the give statement is true
Learn more about paired samples here
brainly.com/question/17143411
#SPJ4
Choose the correct simplification of the expression −5x2(4x − 6x2 − 3). 30x4 − 20x3 15x2 −11x4 − x3 − 8x2 −30x4 20x3 − 15x2 30x4 20x3 15x2.
Answers
Answer:
30 x^4 - 20 x^3 + 15 x^2 is the only valid one however it's not the best simplification.
Step-by-step explanation:
Simplify the following:
-5 x^2 (-6 x^2 + 4 x - 3)
Hint: Factor a minus sign out of -6 x^2 + 4 x - 3.
Factor -1 out of -6 x^2 + 4 x - 3:
-5 x^2×(-(6 x^2 - 4 x + 3))
Hint: Multiply -5 and -1 together.
-5 (-1) = 5:
Answer: 5 x^2 (6 x^2 - 4 x + 3)
Answer:
30 x^4 - 20 x^3 + 15 x^2
Step-by-step explanation: