What is the vertex of this quadratic function?
A) (-4, 0)
B) (-2, 0)
C) (-3, 1)
D) (0, -8)

Answers
Answer:
C) (-3,1) is the solution
Related Questions
johnny is a very picky eater, so he likes to use a lot of condiments. he has ketchup, salt, pepper, and shredded cheese at his disposal. his mother tells him he may only make two additions to his meal (i.e., he can add condiments only twice, regardless of whether or not he already used them). how many different ways can johnny improve his meal?
Answers
Johnny can improve his meal in 6 different ways by choosing two condiments from his four options. Some examples of the different combinations include ketchup and salt, ketchup and pepper, salt and pepper, and so on.
To determine the number of different ways Johnny can improve his meal using condiments, we can use the concept of combinations.
Since Johnny can only make two additions to his meal, we need to find the number of combinations of condiments he can choose from his four options: ketchup, salt, pepper, and shredded cheese.
To calculate the number of combinations, we can use the formula for combinations:
nCr = n! / (r! * (n - r)!)
Where n represents the total number of items and r represents the number of items to be chosen.
In this case, n is 4 (since Johnny has four condiment options) and r is 2 (since Johnny can only make two additions).
Plugging these values into the formula, we get:
4C2 = 4! / (2! * (4 - 2)!)
Simplifying this expression:
4C2 = 4! / (2! * 2!)
The exclamation mark (!) represents the factorial operation, which means multiplying a number by all positive integers less than itself down to 1.
Calculating the factorials:
4! = 4 * 3 * 2 * 1 = 24
2! = 2 * 1 = 2
Substituting these values back into the equation:
4C2 = 24 / (2 * 2)
Simplifying further:
4C2 = 24 / 4
Finally, dividing:
4C2 = 6
Therefore, Johnny can improve his meal in 6 different ways by choosing two condiments from his four options. Some examples of the different combinations include ketchup and salt, ketchup and pepper, salt and pepper, and so on.
To know more about combinations refer here:
https://brainly.com/question/31586670
#SPJ11
What is the magnitude of ?
V
(9,-4)
Answers
Answer:
The magnitude is sqrt((-4)^2 + (-9)^2) = 9.85. The angle is atan(-9/-4) = 180 deg + 66 deg = 246 deg = -114 deg.
Step-by-step explanation:
hope it help
Answer:
9.85
Step-by-step explanation:
|v|= √9²+(-4)²
=√81+16
=√97
|v|= 9.85
Given integer vector x has 5 elements with values 4, 7, 3, 0, 8. what are the ending values in x? int i; for (i = 0; i < x.size() - 1; i) { x.at(i) = x.at(i 1); }
Answers
The ending values in vector `x` after executing the given code snippet would be `7 3 0 8 8`.
The given code snippet appears to be incorrect and incomplete. There are a few issues:
1. The loop condition is not properly defined. Instead of `i < x.size() - 1`, it should be `i < x.size() - 1` to ensure that `i` does not exceed the valid index range of the vector `x`.
2. The increment expression `i` is missing in the loop statement, causing an infinite loop since `i` never changes.
Assuming the correct loop condition is `i < x.size() - 1` and the missing increment expression is `i++`, let's correct the code:
cpp
#include <iostream>
#include <vector>
int main() {
std::vector<int> x = {4, 7, 3, 0, 8};
int i;
for (i = 0; i < x.size() - 1; i++) {
x.at(i) = x.at(i + 1);
}
// Printing the modified vector x
for (int element : x) {
std::cout << element << " ";
}
std::cout << std::endl;
return 0;
}
Now, running this corrected code will give the following output:
7 3 0 8 8
After executing the loop, the vector `x` will have the ending values `7, 3, 0, 8, 8`. The last element `x.at(4)` is assigned the value of `x.at(4 + 1)`, which is `8`.
Learn more about loop here: https://brainly.com/question/32065825
#SPJ11
grade 4 nbt 6 there are 623 guests attending a dinner show. each table seats eight guests. what is the least number of tables needed to seat all of the guests?
Answers
78 is the least number of tables needed to seat all the guests.
Dividing the total number of guests, 623, by the number of guests to sit per table, which is 8 guests per table, one gets 77.78 tables, rounded up to the nearest whole number, and the number is 78 tables.
The reason for rounding up is that the number of tables must be a whole number and not with a fraction or a decimal point. The first 77 tables will have all the spots fully occupied with 8 guests each, but the last table will have 7 guests with one unoccupied spot.
Read more about division operations.
https://brainly.com/question/21172264?referrer=searchResults
#SPJ4
true or false: as the level of confidence increases the number of item to be included in a sample will decrease when the error and the standard deviation are held constant.
Answers
The given statement "As the level of confidence increases the number of item to be included in a sample will decrease when the error and the standard deviation are held constant." is False because error increases.
As the level of confidence increases, the required sample size will increase when the error and standard deviation are held constant.
This is because as the level of confidence increases, the range of the confidence interval also increases, which requires a larger sample size to ensure that the estimate is precise enough to capture the true population parameter with the desired level of confidence.
For example, if we want to estimate the mean height of a population with a 95% confidence interval and a margin of error of 1 inch, we would need a larger sample size than if we were estimating the same mean height with a 90% confidence interval and the same margin of error.
The larger sample size ensures that the estimate is more precise and that we have a higher level of confidence that it captures the true population parameter.
To learn more about confidence click on,
https://brainly.com/question/31317533
#SPJ4
Find the value of cos J rounded to the nearest hundredth, if necessary.

Answers
Answer:
cosJ ≈ 0.38
Step-by-step explanation:
This is a 5- 12- 13 right triangle
with HI = 12, HJ = 13, IJ = 5
cosJ = \(\frac{adjacent}{hypotenuse}\) = \(\frac{IJ}{HJ}\) = \(\frac{5}{13}\) ≈ 0.38 ( to nearest hundredth )
The required value of Cos(J) for the given triangle is 0.38.
What is Pythagoras theorem?Pythagoras theorem states that in a right angled triangle, the sum of the squares of the perpendicular and base is equal to the square of the hypotenuse. It can be written as h² = p² + b².
In the given ΔHIJ the sides are given as,
JH = 13 and HI = 12.
Now, apply Pythagoras theorem to obtain,
IJ² + HI² = JH²
⇒ IJ² = 13² - 12²
⇒ IJ = 5
Use trigonometric ratio to obtain,
Cos(J) = IJ/HI = 5/13 = 0.38
Hence, the value of Cos(J) is obtained as 0.38.
To know more about Pythagoras theorem click on,
https://brainly.com/question/343682
#SPJ2
Lee cada situacion y escribe la razon correspondiente
Answers
3. A box with a top has a square base of side x and height y. If the surface area is 20 in?, what is the largest possible volume of the box?4. A rectangular box with a square base and no top is to have a volume of 500 cubic inches. Find the dimensions for the box that require the least amount of material.
Answers
To find the largest possible volume of the box with a top and square base of side x and height y, we need to optimize the volume V = x^2y subject to the constraint that the surface area A = 20 in^2.
The surface area of the box consists of the area of the base plus the area of the four sides. Since the base is square, the area of the base is x^2, and the area of each side is xy. So we have:
A = x^2 + 4xy = 20
Solving for y in terms of x, we get:
y = (20 - x^2)/(4x)
Substituting this expression for y into the volume formula, we get:
V = x^2(20 - x^2)/(4x) = 5x^2 - 1/4x^3
To optimize this function, we take the derivative with respect to x:
V' = 10x - 3/4x^2
Setting this equal to zero and solving for x, we get:
10x - 3/4x^2 = 0
x = 2.5 or x = 0 (but x can't be 0 because it's the side of the base)
So x = 2.5 is a critical point. To determine whether this is a maximum or a minimum, we can use the second derivative test:
V'' = 10 - 3/x^3
V''(2.5) = 10 - 3/(2.5)^3 = -0.48 < 0
Since V''(2.5) is negative, we know that x = 2.5 is a local maximum. Therefore, the largest possible volume of the box is achieved when x = 2.5 and y = (20 - 2.5^2)/(4(2.5)) = 1.875 in, and the maximum volume is V(2.5) = 5(2.5)^2 - 1/4(2.5)^3 = 15.625 in^3.
To find the dimensions for the rectangular box with a square base and no top that requires the least amount of material, we need to optimize the surface area of the box subject to the constraint that the volume is 500 cubic inches.
Let x be the side length of the square base, and let y be the height of the box. Then the volume is V = x^2y = 500, and the surface area is A = 2x^2 + 4xy. Solving for y in terms of x, we get:
y = 500/x^2
Substituting this expression for y into the surface area formula, we get:
A = 2x^2 + 4x(500/x^2) = 2x^2 + 2000/x
To optimize this function, we take the derivative with respect to x:
A' = 4x - 2000/x^2
Setting this equal to zero and solving for x, we get:
4x - 2000/x^2 = 0
x^3 = 500
x = (500)^(1/3) ≈ 8.658
So x ≈ 8.658 is a critical point. To determine whether this is a minimum or a maximum, we can use the second derivative test:
A'' = 4 + 4000/x^3
A''(8.658) = 4 + 4000/(8.658)^3 ≈ 5.66 > 0
Learn more about Volume here:- brainly.com/question/463363
#SPJ11
Please help :) Please help :)

Answers
Answer:
2
Step-by-step explanation:
Answer:
Step-by-step explanation:
an automated weight monitor can detect underfilled cans of beverages with probability 0.98. what is the probability it fails to detect an underfilled can for the first time when it encounters the 10th underfilled can?
Answers
The probability it fails to detect an underfilled can for the first time when it encounters the 10th underfilled is \(0.01667496\).
What is probability?
Probability is defined as the possibility of an event to occur.
An automated weight monitor can detect underfilled cans of beverages with probability \(0.98\)
Thus probability of success will be \(p=0.98\)
So probability of failure \(q=1-p=1-0.98=0.02\)
To find the first wrong detection happening on the tenth trial the first nine trials must be success followed by failure in the tenth trial.
Thus, required probability \(=p^9q^1=(0.98)^9(0.02)=0.01667496\)
Hence the probability it fails to detect an underfilled can for the first time when it encounters the 10th underfilled is \(0.01667496\).
To know more about probability from given link,
https://brainly.com/question/24756209
#SPJ4
differentiative
2x-3
2x+1
Answers
The differential equation is 8x-4 when the equation is (2x-3)(2x+1).
Given that,
The equation is (2x-3)(2x+1)
We have to find the differentiative equation.
Calculus differentiates the process of locating a function's derivatives. A derivative is the pace at which one function changes in relation to another. Sir Isaac Newton set the foundations for the laws of differential calculus. Numerous scientific disciplines make use of the limits and derivatives ideas. The essential ideas of calculus are differentiation and integration.
Differentiation is the rate at which one quantity changes in relation to another.
Take the equation
(2x-3)(2x+1)
We can do in two ways
1st way
Multiply
4x²+2x-6x-3
Subtraction
4x²-4x-3
Differentiation
8x-4
The equation is 8x-4.
2nd way
We have a formula in differentiation that is
u.v=uv'+vu'
Take u as 2x-3 and v as 2x+1
(2x-3)(2)+(2x+1)(2)
4x-6+4x+2
8x-4
Therefore, The differential equation is 8x-4 when the equation is (2x-3)(2x+1).
To learn more about differentiation visit: https://brainly.com/question/24898810
#SPJ1
What is the correct simplification of
2(3x + 5)?
Answers
Answer: 6x+10
Step-by-step explanation:
honestly i looked it up hope it helps:)
Solve the proportion: 35/8 = 105/x
I will give brainiest if u friend me and dm for answers
Answers
Answer:
x=24
Step-by-step explanation:
35x = 105x8
35x=840
x=24
if the equation is 35/8 = 105/x= then your answer is x=24
Write an equation of the line in slope-intercept form.

Answers
Answer: y = -0.5x + 1
In an election to choose a class representative, the winner got 4 more votes than the second candidate. If 40 learners voted and the winner goy y votes. Find:
a) The number of votes the winner got
b) The number of votes the second candidate got
Answers
In the given problem, the number of votes the winner got is 22. Also, the number of votes the second candidate got is 18.
How to Solve the Problem?Below is the step by step solution to the problem:
a) To get the amount of votes the winner got, we need form an equation based on the given information.
Let us suppose that the second candidate obtained x votes. According to the problem, the winner received four more votes than the runner-up. As a result, the winner received x + 4 votes.
Given that 40 students voted, the total number of votes cast for both candidates should be 40:
x + (x + 4) = 40
Simplifying the equation:
2x + 4 = 40
2x = 40 - 4
2x = 36
x = 36 / 2
x = 18
Therefore, the second candidate received 18 votes.
b) Now that we know the number of votes the second candidate received, we can get the number of votes the winner got:
Winner's votes = x + 4
Winner's votes = 18 + 4
Winner's votes = 22
So, the winner received 22 votes.
Learn more about word problem here: https://brainly.com/question/21405634
#SPJ1
Then, give an example of when "the square root of a
whole number is irrational" IS NOT TRUE.
Answers
Answer:
The square root is not an example when a number is not part of the following number meaning that the correct indirection of the longitude is the correctness of the featured position on the term to term sequence
Determine The Period

Answers
Check the picture below.
notice, if we start checking its pattern from the 10th unit, backwards, it begins to repeat at the unit 4, namely, every 6 units.

help please i dont get these and please show work if u can thxs


Answers
Answer:
Step-by-step explanation:
A = 180°-90°-50° = 40°
Use Law of Sines to find a:
a = b⋅sinA/sinB ≈ 20.1 units
Use Pythagorean Theorem to find c:
c = √(a² + b²) ≈ 31.3 units
:::::
sin(x) = 16/25
x = arcsin(16/25) ≈ 39.8°
Question is in the picture (will give brainlyest)

Answers
Answer:
The answer is c.
Solve the equation: (3)/(7)-(2)/(5)x=5
Answers
Answer:
x = - \(\frac{80}{7}\)
Step-by-step explanation:
Given
\(\frac{3}{7}\) - \(\frac{2}{5}\) x = 5
Multiply through by 35 ( the lcm of 7 and 5 ) to clear the fractions
15 - 14x = 175 ( subtract 15 from both sides )
- 14x = 160 ( divide both sides by - 14 )
x = \(\frac{160}{-14}\) = - \(\frac{80}{7}\)
48:08 bok sk onces Problem 3-12 (Static) The following equation summarizes the trend portion of quarterly sales of condominiums over a long cycle. Sales also exhibit seasonal variations. Ft 40-6.5t+2t
Answers
The seasonal problem may be predicted using the difference between actual sales and the trend portion of the sales as given by the equation: \(Ft 40-6.5t+2t².\)
Solving the given equation: \(Ft = 40 - 6.5t + 2t²\)Hence, the trend portion of quarterly sales of condominiums over a long cycle is given by the equation\(Ft = 40 - 6.5t + 2t²\) where t is time in quarters (Q1 1981 is t=1, Q2 1981 is t=2, Q3 1981 is t=3, etc.)
Given that sales exhibit seasonal variations, the seasonal problem may be predicted using the difference between actual sales and the trend portion of the sales as given by the equation Ft = 40 - 6.5t + 2t².
To know more about the word variations visits :
https://brainly.com/question/11333978
#SPJ11
Relate the area of the square to the length of each side.

Answers
The area of a square can be found by using the following expression:
\(A=l^2\)where "A" is the area and "l" is the length of each side of the square. The square on this problem has an area of 9 cm², so we can find the sides by replacing A for 9 on the expression above.
\(\begin{gathered} 9=l^2 \\ l^2=9 \end{gathered}\)To solve it we need to take the square root on both sides of the equation.
\(\begin{gathered} \sqrt[]{l^2}=\sqrt[]{9} \\ l=\sqrt[]{9} \\ l=3\text{ cm} \end{gathered}\)Each side of the square has a length of 3 cm, so the sides are 3 cm x 3 cm.
DO THESE ON A PIECE OF PAPER! PLEASE HELP! QUICK!!DO ALL OF THEM!!!

Answers
Answer:
A.) 93
B.) 77
C.) 369
Step-by-step explanation:
Answer:
Its the same one that I answered lol
Step-by-step explanation:

Which choice is NOT a fillet type in SOLIDWORKS? constant size variable size faceangled
Answers
The correct option is (d) Angled. Among all (constant size, variable size, face, angled) The Angled is NOT a fillet type in SOLIDWORKS.
SOLIDWORKS has 3 types of fillets: constant size, variable size, and face. Constant size fillets have a constant radius applied to all edges of the selected face or faces. Variable size fillets allow the user to customize the radius of each edge. Face fillets are used to create a smooth transition between two faces.
All three types of fillets create a smooth transition between the edges and faces of a 3D model. Angled is not a type of fillet in SOLIDWORKS, but rather it is a type of chamfer, which is a type of edge treatment that creates an angled edge rather than a smooth transition. Chamfers can be used to create sharp corners or to break up the edges of a 3D model.
To know more about Chamfers:
brainly.com/question/883430
#SPJ4
Help me please!!!!!!!

Answers
Answer:
900 cubes with side of 1/10 ft will fill the prism completely for a total volume of 9/10 ft ³
Answer:
total volume=l×b×h=1 1/2×1 1/5×1/2=3/2×6/5×1/2
=18/20=9/10ft³
I think
Just please help I don’t know

Answers
2. Find the measurement of QP:
a) 22
3x + 9
6x
b) 3
R
c) 6
d) 18
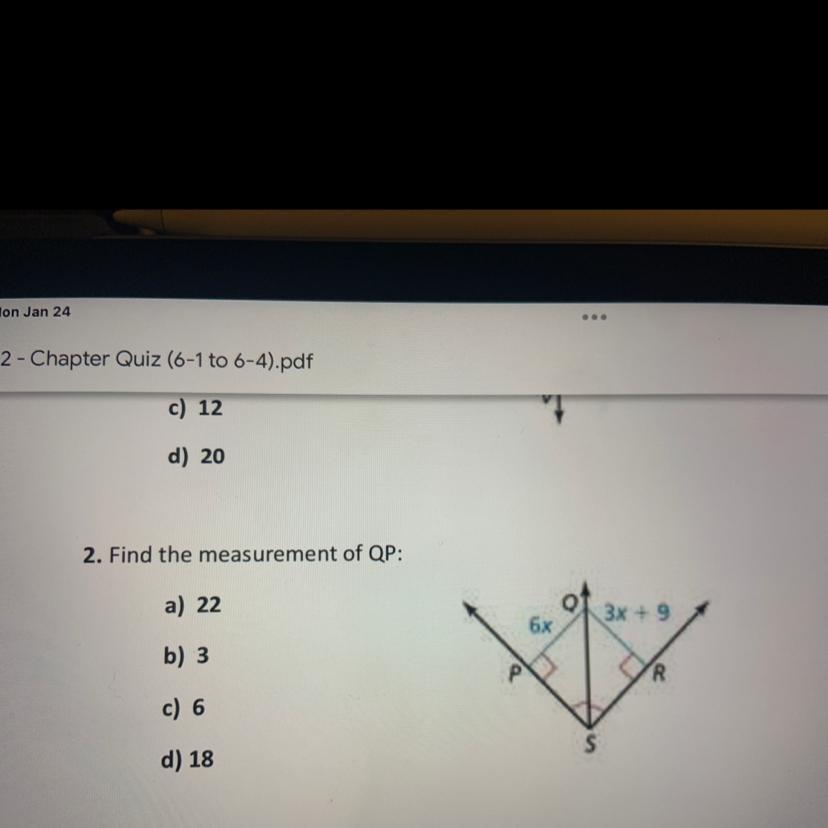
Answers
6x=3x+9
this gives u x=x
so QP=6(3)
QP=18
Which of the following terms correctly describe the object below?
Check all that apply.
a. polyhedron
b. pyramid
c. prism
d. solid
e. cube
f. polygon
*will mark brainliest :))

Answers
Answer:
The given figure is:
a. Polyhedron
c. prism
d. solid
Step-by-step explanation:
First of all, let us consider the given image.
It is a 3 dimensional figure.
It has 2 equal bases which are pentagonal.
Its faces are made along the sides of the bases and are rectangular in shape.
Now, let us classify the given image in following:
a. Polyhedron:
A polyhedron is a 3-D (three dimensional) shape in which there are flat faces.
The faces can be of 'n' number of edges (Polygonal faces).
Its edges are straight, has sharp corners which are also known as vertices.
The given image is a polyhedron as per above definition.
b. Pyramid:
It is also a 3D shape which can have a polygonal base and its faces are triangular which converge on the top to one point.
The given image does not converge to a point on the top, so not a pyramid.
c. Prism:
It is a 3D shape which has it two bases as polygonal structure.
The two bases are equal in shape and size.
There are faces on the body of prism which are formed by joining the edges of the bases.
The given image is a prism with pentagonal bases.
d. Solid:
Any 3D image is called a solid and has a length, width and height.
So, the given image is a Solid.
e. Cube:
Cube is a 3D figure, which has all its faces in square shape.
All the sides are equal for a cube.
The given image is not a cube.
f. Polygon:
A polygon is a closed figure in 2 dimensions which has n number of sides.
The given image is not a polygon.
Answer: The given figure is:
a. Polyhedron
c. prism
d. solid
The given figure is a Polyhedron, prism and solid.
What is a polyhedron?A polyhedron is a three-dimensional geometry having plane surfaces connected together with sharp edges and pointed vertices.
First of all, let us consider the given image. It is a 3-dimensional figure. It has 2 equal bases which are pentagonal. Its faces are made along the sides of the bases and are rectangular in shape.
Now, let us classify the given image in the following:
a. Polyhedron:
A polyhedron is a 3-D (three dimensional) shape in which there are flat faces. The faces can be of 'n' number of edges (Polygonal faces). Its edges are straight, has sharp corners which are also known as vertices. The given image is a polyhedron as per the above definition.
c. Prism:
It is a 3D shape which has it two bases as a polygonal structure.The two bases are equal in shape and size. There are faces on the body of prism which are formed by joining the edges of the bases. The given image is a prism with pentagonal bases.
d. Solid:
Any 3D image is called a solid and has a length, width and height. So, the given image is a Solid.
To know more about Polyhedrons follow
https://brainly.com/question/24324783
#SPJ5
pls explain how to do this

Answers
This is obvious that if Rachel only went 9 miles in 1 hour, and Amos traveled 12 miles in 1 hour, and we need to find out how far apart they will be, we can create the equation of:
12 - 9 = 3, meaning they will be 3 miles apart after one hour.
For an explanation, if you look closely, this is extremely easy. It actually tells you how far they go in one hour, as MPH stands for Miles Per Hour. It tells you that Rachel travels 9 hours in an hour and Amos travels 12 hours in an hour. They left at the same exact time from the same point... so you just need to calculate the difference between 12 and 9, which is 3!
Answer:
They are 15 miles apart.
Step-by-step explanation:
We can use the Pythagorean theorem.
The distance up is 12.
And the distance right and left is 9.
Using a^2 + b^2 = c^2 where a and b are the legs and c is the hypotenuse,
9^2 + 12 ^2 = c^2
81+144 = c^2
225= c^2
Taking the square root of each side,
sqrt(225) = sqrt(c^2)
15 = c
They are 15 miles apart.
What is that y intercept? Can someone please explain to me how to do this and how you got the answer.
