Circle A has a diameter of 9 cm Circle B has a radius of 5 cm which Circle has the largest circumference and about how many centimeters larger is it
Answers
Answer:
circle b and it is bigger by 1 centimeter
Step-by-step explanation:
since circle b has a radius of 5 and radius is have of the diameter you have to do 5+5 to get the diameter when you do that you get 10 and then you have to subtract circle a diameter which is 9 from circle b diameter which is 10 so 10-9 is 1
Answer: Circle B
1.since circle b has a radius of 5 and radius is have of the diameter you have to do 5+5 to get the diameter when you do that you get 10 and then you have to subtract circle a diameter which is 9 from circle b diameter which is 10 so 10-9 is 1
Related Questions
Which of the two graphs below show an outlier in the distribution of the quantitative variable? a) Boxplot only b) Both Histogram and Boxplot c) Neither d) Histogram only
Answers
To determine which of the two graphs (Boxplot and Histogram) shows an outlier in the distribution of the quantitative variable, we need to understand the characteristics of outliers in each type of graph.
An outlier is a data point that significantly deviates from the rest of the data in a distribution. Here's how outliers are represented in Boxplots and Histograms:
a) Boxplot only: If an outlier exists in the distribution, it will be shown as a separate data point outside the whiskers (the lines extending from the box) in the Boxplot. The Boxplot provides a visual representation of the quartiles and any outliers present.
b) Both Histogram and Boxplot: If an outlier exists in the distribution, it may be evident in both the Histogram and the Boxplot. The Histogram shows the frequency or count of data points in each bin or interval, and an outlier can be observed as an extreme value far from the majority of the data. In addition, the Boxplot will display the outlier as mentioned above.
c) Neither: If there are no outliers in the distribution, neither the Histogram nor the Boxplot will show any data points or indicators outside the expected range. The data points will be distributed within the usual range of the distribution, and no extreme values will be present.
d) Histogram only: In some cases, an outlier may be noticeable in the Histogram but not explicitly shown as a separate data point in the Boxplot. This can happen when the outlier is not extreme enough to be considered as an outlier based on the specific criteria used to determine outliers in the Boxplot.
Without examining the actual graphs or having specific information about the data, it is not possible to determine with certainty which option (a, b, c, or d) is correct. To make a definitive determination, you would need to analyze the graphs and assess the presence of extreme values that deviate significantly from the majority of the data.
Learn more about Boxplot and Histogram at https://brainly.com/question/33001489
#SPJ11
1) Colligative properties are best described as what?(Choose the correct option)a. Properties that depend on the size of the systemb. Properties that depend only on the concentration of the solutec. Properties of a colloid
Answers
Colligative properties depends on Properties that depend only on the concentration of the solute.
What is Colligative properties?Colligative Characteristics Colligative qualities of solutions are characteristics that depend on the quantity of molecules or ions in the solute, but not on the kind of solute. Osmotic pressure, boiling point elevation, freezing point depression, and vapour pressure reduction are examples of ligand-like properties.
Given:
As, Colligative qualities of solutions are characteristics that depend on the quantity of molecules or ions in the solute, but not on the kind of solute.
Osmotic pressure, boiling point elevation, freezing point depression, and vapour pressure reduction are examples of ligand-like properties.
So, Colligative properties are dependent only on the number of non-volatile solute molecules or the concentration. They are independent of any other factor.
Learn more about Colligative Property here:
https://brainly.com/question/29971068
#SPJ1
Write an equation of the line passing through point P(-8, 0) that is perpendicular to the line 3x - 5y = 6.
y =
Answers
Answer:
y = -5/3x - 6/5
Step-by-step explanation:
Brainliest pls
You wish to estimate the size of a population of rabbits living in a large urban park. What is the best method to use? A. Count individual rabbits within a randomly placed set of quadrants B. Count individual rabbits along a randomly placed series of transects C. Capture a set of rabbits, mark and release them, and then recapture a second set of rabbits D. Set up a life table for the rabbit population
Answers
The best method to estimate the size of a population of rabbits living in a large urban park is the Capture a set of rabbits, mark and release them, and then recapture a second set of rabbits, which is option C.
Later, a second sample of rabbits is captured, and the number of marked rabbits in this sample is recorded. The ratio of marked rabbits to the total number of rabbits in the second sample can be used to estimate the total population size.
The CMR method is considered one of the most accurate methods for estimating the size of a population of animals, as it accounts for the potential biases in other methods like counting individual animals within quadrants or along transects.
This method assumes that the marked and unmarked animals have an equal chance of being captured and that there is no migration or mortality between the two sampling periods.
In conclusion, the CMR method is the best option to estimate the size of a rabbit population in a large urban park as it is more accurate than other methods and accounts for potential biases in other methods. Therefore, correct option is C.
To learn more about estimate click on,
https://brainly.com/question/31149306
#SPJ4
FInd the Slope and y-intercept
3y-x=18
Answers
Answer:
The slope is 1/3 and the y intercept is 6
Step-by-step explanation:
The slope intercept form of a line is
y = mx+b where m is the slope and b is the y intercept
3y -x =18
Add x to each side
3y = x+18
Divide each side by 3
3y/3 = x/3 +18/3
y = 1/3x +6
The slope is 1/3 and the y intercept is 6
We need to solve for y (y = mx + b):
3y - x = 18
~Add x to both sides
3y = 18 + x
~Divide 3 to everything
y = 6 + x/3 or y = 6 + 1/3/x
So... 1/3 is the slope and 6 is the y-intercept.
Best of Luck!
Hiiioo!! Could someone please help me out!<3 thank you!
-Boopy:)

Answers
Answer:
y = -2x
Step-by-step explanation:
When it is x is -5, y is double of x multiplied into -1.
Hence, it is y = -2x
We can take a couple examples,
i) When x = -5,
y = -2(-5)
= 10
ii) When x = -10,
y = -2(-10)
= 20
and so on.
Feel free to mark this as brainliest! :D
My street hockey team plays three games each week. My team lost all 12 games in the first four weeks. Then, my team won two games and lost one game in the fifth week, bringing our record to 2 wins and 13 losses. Each week after that, my team won two games and lost one game. My team first wins at least 50% of all its games by the end of the first n weeks. What is n?
Answers
Using proportions, it is found that the value of n is of \(n \geq 11\).
What is a proportion?A proportion is a fraction of a total amount, and the measures are related using a rule of three. Due to this, relations between variables, either direct or inverse proportional, can be built to find the desired measures in the problem.
On the first 15 games, the team wins 2 games and losses 13. Then, in each week, the team plays 3 games, winning 2. Then:
After n weeks, the team will have won 2 + 2n games.After n weeks, the team will have played 15 + 3n games.The proportion of wins is given as follows:
\(\frac{2 + 2n}{15 + 3n}\)
The proportion is of at least 50%, hence:
\(\frac{2 + 2n}{15 + 3n} \geq 0.5\)
We solve the inequality for n, similarly to how we would solve an equality, applying cross multiplication. Then:
\(2 + 2n \geq 7.5 + 1.5n\)
\(0.5n \geq 5.5\)
\(n \geq \frac{5.5}{0.5}\)
\(n \geq 11\)
The value of n is of \(n \geq 11\).
More can be learned about proportions at https://brainly.com/question/24372153
#SPJ1
A local rectangular shaped pool used by lap swimmers has dimensions 25 yd by 25 yd and is 5.7 feet deep. Find the cost for filling the pool if the city charges $1.50 per 1000 gallons. Use the conversion 1 gallon
Answers
By calculating the volume of the pool and considering the cost per 1000 gallons of water, we determined that it would cost $286.70 to fill the pool.
Dimensions of rectangular pool: 25 yd by 25 yd
Depth of pool: 5.7 feet
Cost per 1000 gallons of water: $1.50
To find:
The cost of filling the pool
First, we need to find the volume of the pool. The volume of a rectangular pool is calculated by multiplying its length, breadth, and depth.
Volume of rectangular pool = length * breadth * depth = 25 yd * 25 yd * 5.7 feet
Since 1 yard is equal to 3 feet, we convert the dimensions from yards to feet:
25 yd = 25 * 3 = 75 feet
Now we can calculate the volume:
Volume of rectangular pool = 75 ft * 75 ft * 5.7 ft = 25537.5 cubic feet
Since 1 cubic foot is equal to 7.48052 gallons, we can convert the volume to gallons:
Volume of rectangular pool = 25537.5 * 7.48052 gallons = 191136.36 gallons
Next, we need to calculate the cost of filling the pool. Given that the cost per 1000 gallons of water is $1.50, we can determine the total cost.
Cost of filling 191136.36 gallons of water = (191136.36/1000) * $1.50 = $286.70
Therefore, the cost of filling the pool is $286.70.
In summary, by calculating the volume of the pool and considering the cost per 1000 gallons of water, we determined that it would cost $286.70 to fill the pool.
To know more about volume
https://brainly.com/question/28058531
#SPJ11
Calculate the value of 2a + 3b if a = -1 and b = 2
Answers
you can buy 7 oranges for 8.50 what is the price per orange
Answers
Answer:
The price of one orande is 1.21.
Step-by-step explanation:
Answer:
Short Version: 1.21
Long Version: 1.21428571
Step-by-step explanation:
Just divide 8.50 by 7
Which equation is correct regarding the measure of ∠1? m∠1 = one-half(a – c) m∠1 = one-half(a c) m∠1 = one-half(b – d) m∠1 = one-half(b d)
Answers
Answer:
<32 - </3 5810-24
Step-by-step explanation:
32
A point is plotted on the number line at 225 . A second point is plotted at −434 .
What is the length of a line segment joining these points?
Enter your answer as a simplified mixed number in the box.
ANSWER:_____ units?
Answers
Answer:
659 units
Step-by-step explanation:
The length of the segment is the distance between the points.
The distance between two points on the number line is the absolute value of the difference between their coordinates. It does not matter in which order you subtract the numbers.
One point has coordinate 225.
Another point has coordinate -434.
Subtract one coordinate from the other and take the absolute value of the difference.
distance = |-434 - 225| = |-659| = 659
Answer: 659 units
Length of given line segment is 659 units
Step-by-step explanation:
Given:
First point plotted on number line = 225
Second point plotted on number line = - 434
Find:
Length of line segment
Computation:
Length of line segment = Distance between two point
(Distance between two point will be added as absolute value)
So,
Length of line segment = |-434| + |225|
Length of line segment = 434 + 225
Length of line segment = 659 units
Learn more:
https://brainly.com/question/23782800?referrer=searchResults
Solve for x ... please help

Answers
Answer:
\(7x + 49 \degree = 2x + 94\degree \\ 7x - 2x = 94\degree - 49 \degree \\ 5x = 45\degree \\ x = \frac{45}{5} \\ x = 9 \\ check \\ 7(9) + 49 = 112\degree \\ 2(9) + 94 = 112\degree\)
Suppose that f(x)=11x2−6x+2. Evaluate each of the following: f′(3)= f′(−7)=
Answers
Answer:
f'(3) = 60
f'(-7) = -160
Step-by-step explanation:
\(f(x)=11x^2-6x+2\\f'(x)=22x-6\\\\f'(3)=22(3)-6=66-6=60\\f'(-7)=22(-7)-6=-154-6=-160\)
\(\dotfill\)Answer and Step-by-step explanation:
Are you interested in finding what f(-3) and f(-7) equal? Let's find out!
The function is f(x) = 11x² - 6x + 2, so f(-3) is:
f(-3) = 11(-3)² - 6(-3) + 2
f(-3) = 11 * 9 + 18 + 2
f(-3) = 99 + 20
f(-3) = 119
How about f(-7)? We use the same procedure:
f(-7) = 11(-7)² - 6(-7) + 2
f(-7) = 11 × 49 + 42 + 2
f(-7) = 539 + 44
f(-7) = 583
\(\dotfill\)
find a cartesian equation for the curve and identify it. r = 2 csc(θ)
Answers
The cartesian equation of the curve \(r=2 \hspace{0.1cm} csc \hspace{0.1cm} \theta\) is \(y=2\).
A Cartesian equation is essential in mathematics. It corresponds to a mathematical formula that expresses the connection between elements as a function of their positions on a plane known as Cartesian.
A two-dimensional coordinate scheme called the Cartesian plane employs a horizontal x-axis and an upward y-axis to identify locations in space.
Given that, \(r=2 \hspace{0.1cm} csc \hspace{0.1cm} \theta\).
So, \(csc\hspace{0.1cm}\theta=cosec \hspace{0.1cm}\theta\).
The equation becomes as follows:
\(r=2cosec\hspace{0.1cm} \theta\)
By using the trigonometric equation \(cosec\hspace{0.1cm} \theta=\frac{1}{sin\hspace{0.1cm}\theta}\), we get
\(r= \frac{2}{sin \hspace{0.1cm} \theta}\)
Multiplying both sides by \(sin\hspace{0.1cm}\theta\), we get
\(r \hspace{0.1cm}sin\hspace{0.1cm}\theta =2\hspace{0.1cm}\frac{sin\hspace{0.1cm}\theta}{sin\hspace{0.1cm}\theta}\)
\(rsin\hspace{0.1cm}\theta=2\)
By the parametric equations \(x=rcos\hspace{0.1cm}\theta\) and \(y=rsin\hspace{0.1cm}\theta\), we get
\(y=2\)
It is a horizantal line.
Hence, the cartesian equation of the curve \(r=2 \hspace{0.1cm} csc \hspace{0.1cm} \theta\) is \(y=2\).
Read more about cartesian equation:
https://brainly.com/question/30857232
The cartesian equation for the curve is: y = 2 This is a horizontal line passing through the point (0,2).
To find a Cartesian equation for the curve given by the polar equation r = 2 csc(θ), we will convert the polar coordinates (r, θ) into Cartesian coordinates (x, y) using the following relationships:
x = r * cos(θ)
y = r * sin(θ)
Step 1: Express r in terms of θ
r = 2 csc(θ)
Step 2: Since csc(θ) = 1 / sin(θ), rewrite the equation as
r = 2 / sin(θ)
Step 3: Express x and y in terms of r and θ
x = r * cos(θ)
y = r * sin(θ)
Step 4: Substitute r from Step 2 into the y equation
y = (2 / sin(θ)) * sin(θ)
Step 5: Simplify the equation
y = 2
The Cartesian equation for the given polar equation is y = 2, which represents a horizontal line passing through the point (0, 2).
Learn more about cartesian equation:
brainly.com/question/11676110
#SPJ11
What is the area of the polygon below?

Answers
Answer:
20 units²
Step-by-step explanation:
I have included the answer as well as an explanation and formula above. Note that the formula is only for area of trapeziums/trapezoids

In parallelogram ABCD, diagonals AC and BD intersect at E. IF BE = 4x - 12 and DE = 2 x + 8, find s.
Answers
Given data
*BE = 4x - 12
*DE = 2x + 8
At the point of intersection AC and BD, "x" is exactly split into halves.
Therefore
\(DE=EB\)Substitute the values in the above expression as
\(\begin{gathered} 2x+8=4x-12 \\ 2x-4x=-12-8 \\ -2x=-20 \\ x=\frac{-20}{-2} \\ x=10 \end{gathered}\)Thus, the value of x equals to 10
Model 1/3 Divide a whole into ___equal __
of the rows to show the fraction__
Answers
Answer:
three parts 1/3
Step-by-step explanation:
2(x+1)=10 what's x please best example
Answers
Answer:
x = 4
Step-by-step explanation:
1.Distribute
2. Subtract 2 from both sides
3. Simplify
4. Divide both sides by same factor
5. Simplify
x = 4
Answer: 4
Step-by-step explanation:
We have to try getting x by itself to solve for it. Since we have two sides that are equal to each other, we can add, subtract, multiply, and divide anything on both sides to try to isolate x.
\(2(x+1)=10\)
We can first divide the left side and the right side by 2. This would remove the 2 being multiplied on the outside.
\(\frac{2(x+1)}{2}=\frac{10}{2}\\x+1=10\div 2\\x+1=5\)
Now, we have a + 1 on the left side that we need to remove to get x by itself. If we are adding something, we can remove that by subtracting the same thing. Hence, we can subtract 1 from both sides to remove the + 1.
\(x+1=5\\x+1-1=5-1\\x+0=4\\x=4\)
After all that simplifying, we get that x equals 4.
A car is traveling at a rate of 60 kilometers per hour. What is the car's rate in miles per hour? How many miles will the car travel in 3 hours? In yourcomputations, assume that 1 mile is equal to 1.6 kilometers. Do not round your answers.
Answers
37.5 mile per hour
112.5 miles
Explanation:rate = 60km per hour
1 mile = 1.6 kilometer
Let's convert:
\(\frac{60\operatorname{km}}{1\text{ hour}}\times\frac{1\text{ mile}}{1.6\operatorname{km}}\)\(\begin{gathered} \frac{60\operatorname{km}}{1\text{ hour}}\times\frac{1\text{ mile}}{1.6\operatorname{km}}\text{ km cancels out, we are left with mile per hour} \\ \text{= }\frac{60\text{ mile}}{1.6\text{ hour}} \\ =\text{ 37.5mile per hour} \end{gathered}\)The car's rate in miles per hour is 37.5 mile per hour
In 1 hour, the car travels 37.5 mile
In 3 hours, the car will travel = 3 × 37.5miles
= 112.5 miles
In 3 hours, the car will travel 112.5 miles
during the first 5 months (151 days) of the provisional period, provisional license holders under the age of 18 a. must not have passengers under the age of 18, unless accompanied by a qualified supervising driver or unless the b. must have all passengers in the front seat. c. may have as many passengers as will fit into their vehicles. d. may only have passengers during daytime hours.
Answers
Provisional license holders under the age of 18 may only have passengers during daytime hours is: P ≤ 18 → P = D
a. Provisional license holders under the age of 18 must not have passengers under the age of 18, unless accompanied by a qualified supervising driver:
The formula for this statement is: P ≤ 18 → S = Q
Where:
P = Age of passengers
S = Supervising driver
Q = Qualified
b. Provisional license holders under the age of 18 must have all passengers in the front seat:
The formula for this statement is: P ≥ 18 → A = F
Where:
P = Age of passengers
A = All
F = Front seat
c. Provisional license holders under the age of 18 may have as many passengers as will fit into their vehicles:
The formula for this statement is: P ≤ 18 → M = W
Where: P = Age of passengers
M = Maximum
W = Will fit into the vehicle
d. Provisional license holders under the age of 18 may only have passengers during daytime hours:
The formula for this statement is: P ≤ 18 → P = D
Where:
P = Age of passengers
P = Passengers
D = Daytime hours
Learn more about daytime hours here:
https://brainly.com/question/4352908
#SPJ4
Helppppppp!!!!!!!!! plzzzzzz!!!!

Answers
9. y=-2x+3
10. y=-1x+7
Which expression represents the greatest factorization of 32w - 56xy
Answers
Answer:
Factor 8 out of 32w - 56xy
8 ( 4w - 7xy )
GCF of 32 and 56 is 8.
So we have 4(8w)-7(8xy)
---
sry if i didn't help
a random sample is normally distributed. if all values in the sample and all values in the population are multiplied by 2, what is the impact on cohen's d?
Answers
Multiplying values by 2 in a normally distributed random sample and population increases the effect size as measured by Cohen's d.
The impact of multiplying all values in a normally distributed random sample and population by 2 on Cohen's d is an increase in effect size. Cohen's d measures the degree of difference between two sets of scores, calculated by dividing the difference between the two means by the pooled standard deviation. Therefore, when values are multiplied by 2, the means increase, leading to an increase in effect size as measured by Cohen's d.
In addition, multiplying values by 2 also increases the magnitude of the standard deviation, which is a measure of spread. When the standard deviation is larger, it requires a larger mean difference for Cohen's d to register a significant effect. Therefore, by increasing the standard deviation, the effect size measure will increase.
To summarize, multiplying values by 2 in a normally distributed random sample and population increases the effect size as measured by Cohen's d. This is because multiplying values by 2 increases both the mean and the standard deviation, which results in a larger mean difference and a larger standard deviation, respectively. Consequently, the effect size measure increases.
See more about normally distributed at: https://brainly.com/question/2579706
#SPJ11
PLEASE HELP ME, Am given 60 points!! NO CAP
What is the ratio of the length of JK to the length of MN?

Answers
In circle with m EFG = 58 and EF = 6 units, find the length of arc EG. Round to the nearest hundredth.

Answers
The length of arc EG is approximately 7.35 units.
To find the length of arc EG, we need to use the formula:
length of arc = (central angle/360°) × 2πr
where r is the radius of the circle and the central angle is in degrees.
We are given that m∠EFG = 58°, and EF = 6 units. Since EF is a chord of the circle, we can use the chord-chord angle theorem to find that m∠EGF = ½(180° - 58°) = 61°.
Now, we can use the Law of Cosines to find the length of GE:
GE² = EF² + FG² - 2(EF)(FG)cos(∠EGF)
GE² = 6² + FG² - 2(6)(FG)cos(61°)
Since FG = 2r (because it is the diameter of the circle),
GE² = 36 + (2r)² - 12r cos(61°)
We can simplify this to:
GE² = 4r² - 12r cos(61°) + 36
GE² = 4(r² - 3r cos(61°) + 9)
Now, we can use the formula for the length of the arc:
length of arc EG = (m∠EGF/360°) × 2πr
length of arc EG = (61/360) × 2πr
length of arc EG = (61/180) × πr
Substituting the expression for GE² in terms of r, we get:
length of arc EG = (61/180) × π √[4(r² - 3r cos(61°) + 9)]
We can now use a calculator to find the approximate value of the length of arc EG.
Rounded to the nearest hundredth, the length of arc EG is approximately 7.35 units.
To know more about properties of circle visit:
brainly.com/question/30066312
#SPJ1
Find the angles between the vectors A with arrow and B with arrow given the following.
(a) A = 2î − 7ĵ, B = -5î + 3ĵ
(b) A = 6î + 4ĵ, B = 3î − 3ĵ
(c) A = 7î + 5ĵ, B = 5î − 7ĵ °
Answers
Answer:Look Down 0D
Step-by-step explanation:I am sorry if this doesn't help but I dont know the answer???
a) The angle between vectors A and B is approximately 154.68 degrees.To find the angles between the vectors A and B,
we can use the dot product formula and the fact that the dot product of two vectors A and B is given by:
A · B = |A| |B| cos(θ)
where |A| and |B| represent the magnitudes of vectors A and B, respectively, and θ is the angle between them.
Let's calculate the angles for each case:
(a) A = 2î − 7ĵ, B = -5î + 3ĵ:
Using the dot product formula:
A · B = (2)(-5) + (-7)(3) = -10 - 21 = -31
The magnitude of A:
|A| = √(2^2 + (-7)^2) = √(4 + 49) = √53
The magnitude of B:
|B| = √((-5)^2 + 3^2) = √(25 + 9) = √34
Now, we can calculate the angle θ using the formula:
-31 = (√53)(√34)cos(θ)
Simplifying:
cos(θ) = -31 / (√53)(√34)
Using inverse cosine (arccos) to find θ:
θ = arccos(-31 / (√53)(√34))
The angle between vectors A and B is approximately θ = 154.68 degrees.
(b) A = 6î + 4ĵ, B = 3î − 3ĵ:
Using the dot product formula:
A · B = (6)(3) + (4)(-3) = 18 - 12 = 6
The magnitude of A:
|A| = √(6^2 + 4^2) = √(36 + 16) = √52 = 2√13
The magnitude of B:
|B| = √(3^2 + (-3)^2) = √(9 + 9) = √18 = 3√2
Now, we can calculate the angle θ using the formula:
6 = (2√13)(3√2)cos(θ)
Simplifying:
cos(θ) = 6 / (2√13)(3√2) = 1 / (√13)(√2)
Using inverse cosine (arccos) to find θ:
θ = arccos(1 / (√13)(√2))
The angle between vectors A and B is approximately θ = 23.38 degrees.
(c) A = 7î + 5ĵ, B = 5î − 7ĵ:
Using the dot product formula:
A · B = (7)(5) + (5)(-7) = 35 - 35 = 0
The magnitude of A:
|A| = √(7^2 + 5^2) = √(49 + 25) = √74
The magnitude of B:
|B| = √(5^2 + (-7)^2) = √(25 + 49) = √74
Now, we can calculate the angle θ using the formula:
0 = (√74)(√74)cos(θ)
Since the dot product is zero, it indicates that the vectors are orthogonal (perpendicular) to each other. In this case, the angle between vectors A and B is θ = 90 degrees.
Therefore, for the given cases:
(a) The angle between vectors A and
B is approximately 154.68 degrees.
(b) The angle between vectors A and B is approximately 23.38 degrees.
(c) The angle between vectors A and B is 90 degrees.
Learn more about vectors here: brainly.com/question/24256726
#SPJ11
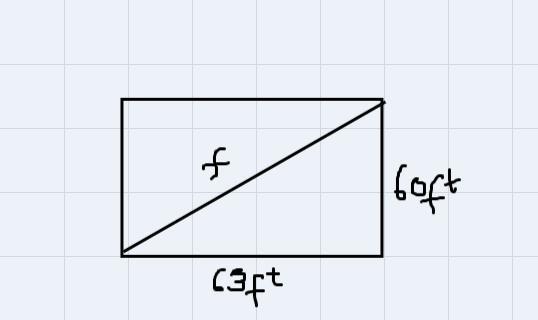
Mia is decorating a ballroom ceiling with garland. If the rectangular ceiling is 63 feet by 60 feet, how much garland will Mia need to reach from one corner of the ceiling to the opposite corner?
Answers
Given the dimensions of the rectangular ceiling below
\(\begin{gathered} \text{length}=63\text{feet} \\ \text{width}=60\text{feet} \end{gathered}\)Let us sketch out the image of the rectangle ceiling.
We are to solve for x, which represents the cost of garland Mia will need to reach from one corner of the ceiling to the opposite corner.
Let us now sketch out the triangular shape from the rectangle.
Using Pythagoras theorem to solve for x,
Therefore,
\(\begin{gathered} x^2=60^2+63^2 \\ x^2=3600+3969 \\ x^2=7569 \\ x=\sqrt[]{7569} \\ x=87\text{feet} \\ \therefore x=87feet \end{gathered}\)Hence, the cost of garland Mia will need to reach from one corner of the ceiling to the opposite corner is 87feet.

Finding the side length of a cube from its Volume in liters A technical machinist is asked to build a cubical steel tank that will hold 275 L of water. Calculate in meters the smallest possible inside length of the tank. Round your answer to the nearest 0.001 m. X 5 ?
Answers
The smallest possible inside length of the cubical steel tank that can hold 275 liters of water is approximately 0.640 meters.
The side length of the cube is found by converting the volume of water from liters to cubic meters, as the unit of measurement for the side length is meters.
Given that the volume of water is 275 liters, we convert it to cubic meters by dividing it by 1000 (1 cubic meter = 1000 liters):
275 liters / 1000 = 0.275 cubic meters
Since a cube has equal side lengths, we find the side length by taking the cube root of the volume. In this case, we find the cube root of 0.275 cubic meters:
∛(0.275) ≈ 0.640
Rounded to the nearest 0.001 meters, the smallest possible inside length of the tank is approximately 0.640 meters.
To know more about smallest possible inside length, refer to the link :
https://brainly.com/question/17304098#
#SPJ11
The time needed to complete a final examination in a particular college course is normally distributed with a mean of 80 minutes and a standard deviation of 10 minutes. Answer the following questions. Round the intermediate calculations for z value to 2 decimal places.
a. What is the probability of completing the exam in one hour or less (to 4 decimals)?
b. What is the probability that a student will complete the exam in more than 60 minutes but less than 75 minutes (to 4 decimals)?
c. Assume that the class has 60 students and that the examination period is 90 minutes in length. How many students do you expect will be unable to complete the exam in the allotted time (to the next whole number)?
Answers
a. Probability of completing the exam in one hour or less is 0.0228. b. Probability of completing the exam in more than 60 minutes but less than 75 minutes is 0.2857. c. About 10 students are expected to be unable to complete the exam in the allotted time.
a. To find the probability of completing the exam in one hour or less, we need to convert one hour (60 minutes) into a z-score using the formula:
z = (x - μ) / σ
where x is the value we want to convert, μ is the mean, and σ is the standard deviation. So, we have:
z = (60 - 80) / 10 = -2
Using a standard normal distribution table or a calculator, we find that the probability of a z-score being less than or equal to -2 is 0.0228 (to 4 decimals). Therefore, the probability of completing the exam in one hour or less is 0.0228.
b. To find the probability that a student will complete the exam in more than 60 minutes but less than 75 minutes, we need to convert both values into z-scores:
z1 = (60 - 80) / 10 = -2
z2 = (75 - 80) / 10 = -0.5
Then, we can find the probability between these two z-scores using a standard normal distribution table or a calculator. The probability is:
P(-2 < z < -0.5) = P(z < -0.5) - P(z < -2)
= 0.3085 - 0.0228
= 0.2857 (to 4 decimals)
Therefore, the probability that a student will complete the exam in more than 60 minutes but less than 75 minutes is 0.2857.
c. We know that the mean time to complete the exam is 80 minutes and the standard deviation is 10 minutes. To find the number of students who will be unable to complete the exam in the allotted time of 90 minutes, we need to find the number of students whose completion time is greater than 90 minutes.
We can convert 90 minutes into a z-score using the formula:
z = (x - μ) / σ = (90 - 80) / 10 = 1
Using a standard normal distribution table or a calculator, we find that the probability of a z-score being greater than 1 is 0.1587.
So, the proportion of students who will be unable to complete the exam in 90 minutes is 0.1587. To find the actual number of students, we can multiply this proportion by the total number of students:
0.1587 x 60 ≈ 9.52
Therefore, we can expect about 10 students to be unable to complete the exam in the allotted time.
Learn more about probability here: brainly.com/question/30034780
#SPJ4