Two lengths of steel are in ratio 8:5 respectively. If the first length is 120m whats the second length
Answers
Answer: 75
Step-by-step explanation:
8/5 = 120/x
Then cross multiply
8x = 120(5)
8x = 600
8x/8 = 600/8
x = 75
Related Questions
how did you solve it??

Answers
Step by step
Perimeter is the sum of all sides
Add
4a + 5a -7 + 7a + 2 + 4a + 3
Combine like terms
(4a + 5a + 7a + 4a) + (-7 +2 +3)
B) 20a -2 is your answer
1/4 x -1/2 =
will give brainest
Answers
Hello,
\( \frac{1}{4} \times- \frac{1}{2} = \frac{1 \times (-1)}{4 \times 2} = - \frac{1}{8} \)
What is the equation of the line that passes through the point (4,1) and has a slope of 1/2 ?
Answers
Answer: 37
Step-by-step explanation: so first you have to realize that i what I’m doing and you not listen to me
need help with math been struggling on this question for a while

Answers
\(\sqrt{192 x^5}\qquad \begin{cases} 192=2\cdot 2\cdot 2\cdot 2\cdot 2\cdot 2\cdot 3\\ \qquad 2^6\cdot 3\\ \qquad 2^{(3)(2)}\cdot 3\\ \qquad (2^3)^2\cdot 3\\ x^5=x^{4+1}\\ \qquad x^4 x^1\\ \qquad x^{(2)(2)}x\\ \qquad (x^2)^2 x \end{cases}\implies ~\hfill \begin{array}{llll} \sqrt{(2^3)^2\cdot 3(x^2)^2x} \\\\\\ 2^3 x^2\sqrt{3x} \\\\\\ 8x^2\sqrt{3x} \end{array}\)
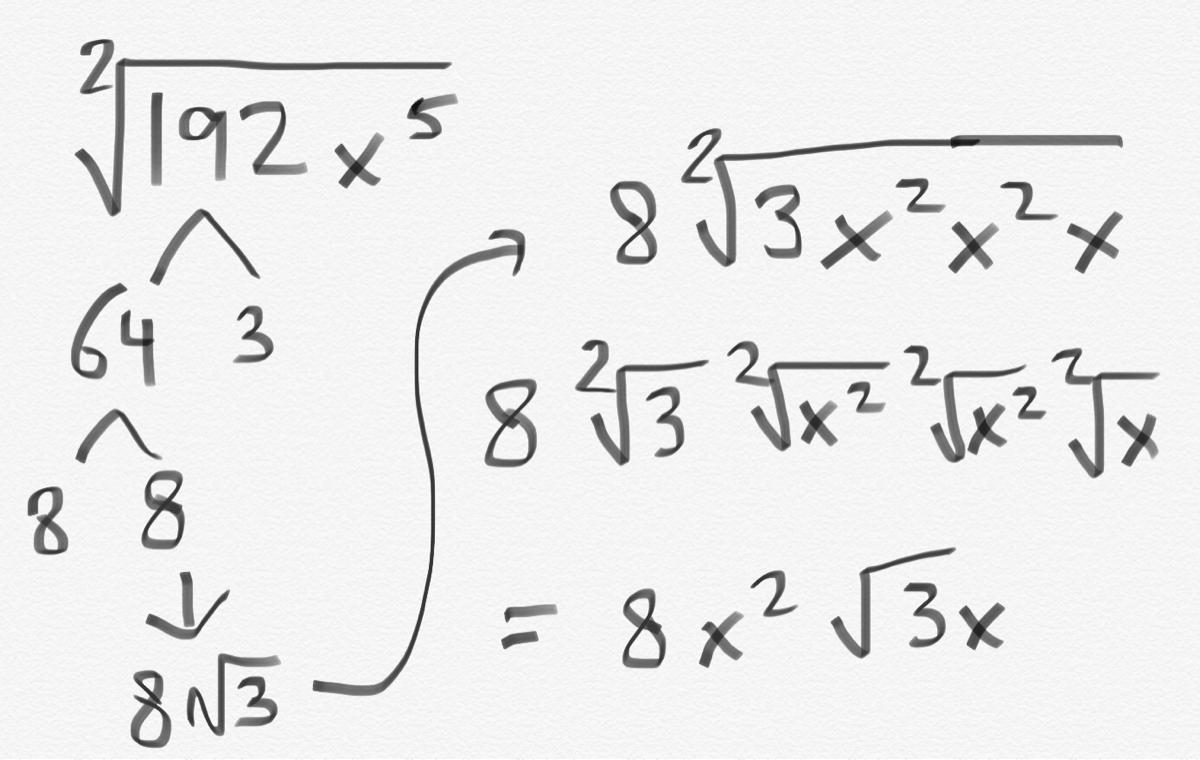
the first possession of each nfl game is decided by a coin toss. is this process deterministic, or truly random?
Answers
A coin toss determines the first possession of each NFL game. This process deterministic not random event because the initial coin flip only determines whether a team receives the ball now at start of the first or third quarter.
What is meant by first possession?Possession in football refers to a team keeping possession of the ball for as longer as possible in order to create opportunities for goals and prevent this same opposition from posing a threat to the team's goal.
Some key features regarding the first possession in NFL game are-
The scoring team wins if the first possession results in such a touchdown (by receiving team or a defensive team on a turnover) or a safety by the defensive team. If the receiving team is unable to score and loses possession, this same game is decided by sudden death, with the first team to score winning.Many NFL fans oppose the current overtime setup in which the winning team can elect to catch the ball, move down the field, and score, effectively ending the game without allowing the opposing team to touch the ball on offense.If the resolution of player decisions results in completely predictable outcomes, the game is deterministic. It is indeterministic to some extent if actions result in potentially chaotic outcomes.To know more about the random events, here
https://brainly.com/question/251701
#SPJ4
can anyone please help me solve!!!!!

Answers
Answer:
30 square units
Step-by-step explanation:
We know that the area of a triangle is equal to half of the product between the base and the height.
In this case, we can see that one of the sides of the triangle is parallel to the x-axis, then we can define:
Base = difference between the two extreme x-values
In this case, the extremes (the point at the left and the point and the right) are:
(-5, 3) and (7, 3)
The difference between the x-values is:
D = (7 - (-5)) = 7 + 5 = 12
Then the base is 12 units long.
For the height, we can find the difference in the y-value between the lowest point and the highest one.
In this case, we have two points at the same height (both with y-value = 3)
and the top point is (4, 8)
The difference in the y-value is:
D = (8 - 3) = 5
Then the height is 5 units.
Now that we know the height and the base of the triangle, the area is:
A = (5 units)*(12 units)/2 = 30 square units.
Simplify -3x^2-5x^2(4x^3-x^2)2
Answers
Let's simplify step-by-step.
−3x2−5x2(4x3−x2)(2)
Distribute:
=−3x2+−40x5+10x4
Answer:
=−40x5+10x4−3x2
Several scientists decided to travel to South America each year beginning in 2001 and record the number of insect species they encountered on each trip. The table shows the values coding 2001 as 1,2002 as 2, and so on. Find the model that best fits the data and identify its corresponding R² value. Year: 1,2,3,4,5,6,7,8,9,10 Species: 47,53,38,35,49,42,60,54,67,82
Answers
it is important to note that the model has a relatively low $R^2$ value, which suggests that there may be other factors that are influencing the number of insect species encountered that are not captured by the linear relationship between year and species.
To find the model that best fits the data, we can begin by plotting the data points and looking for any patterns. However, since we have ten data points, it may be easier to use a regression model to find the best fit.
We can use a linear regression model of the form $y = mx + b$, where $y$ represents the number of insect species and $x$ represents the year. We can use a tool such as Excel or a calculator with regression capabilities to find the values of $m$ and $b$ that minimize the sum of the squared errors between the predicted values and the actual values.
Using Excel, we find that the regression equation is $y = 5.66x + 40.6$, with an $R^2$ value of 0.304. This indicates that the linear model explains about 30.4% of the variability in the data, which is a relatively low value.
To interpret the model, we can say that on average, the number of insect species encountered each year increases by 5.66.
To learn more about data visit:
brainly.com/question/10980404
#SPJ11
Use the function below to find (-2).
f(x) = 3x
O A.
O B. -9
O c.
O D. -6
Answers
answer
f(x)= 3x
= 3×-2 = -6
D. -6
Use The Properties Of Integrals And ∫13exdx=E3−E To Evaluate ∫13(3ex−2)Dx.
Answers
The value of the integral ∫[1,3] (3ex - 2) dx is 3(e3 - e) - 4. The bolded keywords are "3(e3 - e) - 4," which represents the evaluated value of the integral using the properties of integrals.
To evaluate the integral ∫[1,3] (3ex - 2) dx, we can use the properties of integrals, specifically linearity and the power rule.
Let's break down the integral and apply the properties:
∫[1,3] (3ex - 2) dx
= ∫[1,3] 3ex dx - ∫[1,3] 2 dx
Using the power rule of integration, the integral of ex with respect to x is simply ex.
∫[1,3] 3ex dx = 3 ∫[1,3] ex dx
Now we can evaluate this integral:
= 3[ex] from 1 to 3
= 3(e3 - e1)
= 3(e3 - e)
Next, let's evaluate the second integral:
∫[1,3] 2 dx = 2 ∫[1,3] dx
The integral of a constant with respect to x is simply the constant times the difference of the limits of integration.
= 2[x] from 1 to 3
= 2(3 - 1)
= 2(2)
= 4
Now, we can combine the results of the two integrals:
∫[1,3] (3ex - 2) dx = 3(e3 - e) - 4
Therefore, the value of the integral ∫[1,3] (3ex - 2) dx is 3(e3 - e) - 4.
In the final answer, the bolded keywords are "3(e3 - e) - 4," which represents the evaluated value of the integral using the properties of integrals.
Learn more about integral here
https://brainly.com/question/30094386
#SPJ11
A Chemistry book is moved 2 meters to the left and then 1 meter to the right. What is the distance travelled?
Answers
Answer:1 meter to the left
Step-by-step explanation: 2-1
what is the solution of the system? use the elimination method. {4x 2y=182x 3y=15 enter your answer in the boxes.
Answers
The solution of the system is x = 4 and y = 1.
To solve the system of equations using the elimination method, we can eliminate one variable by adding or subtracting the equations.
In this case, we can eliminate the variable "x" by multiplying the first equation by -2 and adding it to the second equation.
1. Multiply the first equation by -2:
-8x - 4y = -36
2. Add the modified first equation to the second equation:
-8x - 4y + 2x + 3y = -36 + 15
Simplifying the equation gives:
-6x - y = -21
3. Solve the new equation for one variable. Let's solve for y:
-y = -21 + 6x
y = 21 - 6x
4. Substitute the value of y into one of the original equations. Let's use the first equation:
4x + 2(21 - 6x) = 18
Simplifying the equation gives:
4x + 42 - 12x = 18
-8x = -24
x = 3
5. Substitute the value of x back into the equation for y:
y = 21 - 6(3)
y = 21 - 18
y = 3
Therefore, the solution to the system of equations is x = 3 and y = 3.
To learn more about elimination method, click here: brainly.com/question/29944642
#SPJ11
the larger circle has center $o$ and passes through $d$. the smaller circle has diameter $od$. what percent of the larger circle's area is gray?
Answers
25% is the larger circle area is gray.
Area of a Circle: The area of a circle is pi times the radius squared.
To calculate the area of the circle we have the formula:
A = π r²-----(1)
where
A=area
r=radius.
First, we have to analyze the given data, the large circle center o passes through d, so
Gray circle area=π*(radius)^2----(2)
The radius of the smaller circle = OD/2 substitute in (2)
Gray circle area=π*(OD/2)^2
Gray circle area=π*OD^2/4
Larger circle area=π*(radius)2
radius of the larger circle = OD
larger circle area=π*OD^2
To know the percentage of a large circle we have a small formula:
gray circle area/large circle area--------(3)
=π*OD^2/4/π*OD^2
=π*OD^2/4*1/π*OD^2=1/4
=25/100
=25%
To know more about the Area of the circle:
https://brainly.com/question/14738425

what does the equation x 2 y 2 = 4 correspond to if a) x, y are the only variables being considered, b) x, y, z are the only variables being considered.
Answers
The equation x² y² = 4 corresponds to a hyperbola when only considering x and y as variables. When considering x, y, and z as variables, the equation corresponds to a two-sheeted hyperboloid.
a) When only x and y are the variables being considered, the equation x² y² = 4 corresponds to a circle in the xy-plane. The circle has a center at the origin (0,0) and a radius of 2.
b) If x, y, and z are the only variables being considered, the equation x² y² = 4 still represents a circle in the xy-plane, but it becomes a cylinder along the z-axis. This cylinder has a center on the z-axis and a radius of 2, extending infinitely along the z-axis.
To know more about hyperbola visit:
https://brainly.com/question/27799190
#SPJ11
The area of the triangle below is 5/12 square feet. What is the length of the base? Express your answer as a fraction in simplest form.
1/2 ft is the height
Answers
Answer:
5/4 ft
Step-by-step explanation:
Given data
Area= 5/12 square feet
Height= 1/2 ft
Base=????
We know that the area of a triangle is given as
Area= (1/2)B*H
substitute
5/12= 1/2* B* 1/2
5/12= B/4
cross multiply
12B= 20
B= 20/12
B= 5/3
Hence the base is 5/4 ft
Find a Cartesian equation for the curve and identify it.
r = 4csc(θ)
circle line parabola ellipse
Answers
The Cartesian equation for the curve r = 4csc(θ) is (x^2 + y^2) * y = 4, and it represents a semi-cubical parabola.
To find a Cartesian equation for the curve r = 4csc(θ) and identify it, we can follow these steps:
Step 1: Rewrite the equation using the definition of cosecant
Cosecant (csc) is the reciprocal of sine, so we can rewrite the equation as:
r = 4/sin(θ)
Step 2: Express r and θ in Cartesian coordinates
We know that r^2 = x^2 + y^2 and y = r * sin(θ). We can use these relationships to replace r and θ with x and y in our equation. First, we solve for sin(θ):
sin(θ) = y / r
Step 3: Substitute sin(θ) and r in the equation
Now, replace sin(θ) and r in the original equation:
r = 4/(y/r)
Step 4: Simplify and solve for y
To get a Cartesian equation, multiply both sides by y:
r * y = 4
Since y = r * sin(θ), we can replace y with r * sin(θ):
r * (r * sin(θ)) = 4
Step 5: Replace r with x^2 + y^2
Since r^2 = x^2 + y^2, we can replace r in the equation:
(x^2 + y^2) * (y) = 4
Step 6: Identify the curve
This equation represents a curve in the Cartesian plane. By analyzing the equation, we can see that it's a semi-cubical parabola.
In conclusion, the Cartesian equation for the curve r = 4csc(θ) is (x^2 + y^2) * y = 4, and it represents a semi-cubical parabola.
Learn more about Cartesian equation
brainly.com/question/11676110
#SPJ11
Definition of a derivative (limit of the difference quotient)
Answers
The derivative of a function f(x) at a point x = a is defined as the limit of the difference quotient as h approaches zero:
f'(a) = lim (h → 0) [f(a + h) - f(a)] / h
What is derivative?
The derivative of a function in calculus measures the function's sensitivity to changes in its input variable. Specifically, at a particular point, it represents the function's rate of change with respect to its input variable at that moment.
The derivative of a function f(x) at a point x = a is defined as the limit of the difference quotient as h approaches zero:
f'(a) = lim (h → 0) [f(a + h) - f(a)] / h
This limit represents the instantaneous rate of change or slope of the function at the point x = a. The difference quotient is the change in the function value divided by the change in the input variable (or the distance between two points on the graph of the function).
The derivative is a fundamental concept in calculus, and it has many applications in various fields of science, engineering, and economics. It allows us to calculate important quantities such as velocity, acceleration, and marginal cost, and it is used to optimize functions and solve many real-world problems.
To learn more about derivative visit:
https://brainly.com/question/30403647
#SPJ4
on average, a textbook author makes two wordprocessing errors per page on the first draft of her textbook. what is the probability that on the next page she will make
Answers
Therefore, the probability that on the next page, the author will make at most two word processing errors is 0.99207367.
To find the probability of making word processing errors, we must use Poisson Distribution.
What is Poisson Distribution?
A Poisson distribution is a probability distribution that estimates the number of occurrences of an event in a fixed time or space interval.
It is used to model a situation where events occur randomly and independently over a fixed period or area.
The Poisson distribution's primary assumptions are that events are rare, random, and that one event does not affect another event's outcome. The Poisson distribution is useful in predicting the number of occurrences of a specific event in a given time or space interval. This distribution is useful in several fields, including finance, insurance, and public health.Now let's solve the given problem,
The probability that there are no word processing errors is given by\(:P (X = 0) = e^ -μμ = 200/500 = 0.4\) (average number of errors per page = 2/5)P (X = 0) = e^ -0.4 = 0.67032005Now, the probability that there are 2 or fewer errors is given by:\(P (X ≤ 2) = ΣP (X = i) i = 0 to 2P (X ≤ 2) = P (X = 0) + P (X = 1) + P (X = 2)P (X ≤ 2) = 0.67032005 + 0.26812802 + 0.0536256P (X ≤ 2) = 0.99207367\)
for such more questions on probability distribution
https://brainly.com/question/24756209
#SPJ11
The parent function, f(x) = 5^x, has been vertically compressed by a factor of one-half, shifted to the left three units and down two unlts.
Choose the correct function to represent the transformation.

Answers
Answer: Choice C
\(\displaystyle g(x) = \left(\frac{1}{2}\right)5^{x+3}-2\)
=====================================================
Explanation:
The 1/2 out front handles the vertical compression by 1/2. For example, if two points are vertically spaced by 10 units, then their new vertical distance is now (1/2)*10 = 5 units.
The x+3 in the exponent means "shift 3 units to the left". Effectively what's going on is that the old input x is now x+3, ie 3 units larger than before. This shifts the xy axis itself 3 units to the right. If we held the curve fixed in place while the xy axis moved like this, then it gives the illusion the curve is moving 3 units to the left.
Then finally the -2 at the very end shifts the curve down 2 units. This is because whatever the y coordinate is, we subtract 2 from it to do this vertical shifting. For example, the point (0,62.5) shifts 2 units down to (0,60.5)
glmm: the final hessian matrix is not positive definite although all convergence criteria are satisfied. the procedure continues despite this warning. subsequent results produced are based on the last iteration. validity of the model fit is uncertain.
Answers
The issue you are experiencing with the final Hessian matrix not being positive definite despite satisfying convergence criteria can occur in Generalized Linear Mixed Models (GLMMs).
When this warning appears, the procedure continues, but the validity of the model fit becomes uncertain. The Hessian matrix is used to assess the curvature of the likelihood function, and if it is not positive definite, it suggests that the model's estimation might be unreliable. It is crucial to interpret the subsequent results with caution as they are based on the last iteration. Consider checking the model's assumptions, reviewing the data, or consulting with a statistician to address this uncertainty.
To know more about matrix visit:
brainly.com/question/31850779
#SPJ11
PLS HELPP I NEED AN ANSWER ASAP ILL GIVE BEAINLIEST

Answers
The top right graph could show the arrow's height above the ground over time.
Which graph models the situation?The initial and the final height are both at eye level, which is the reference height, that is, a height of zero.
This means that the beginning and at the end of the graph, it is touching the x-axis, hence either the top right or bottom left graphs are correct.
The trajectory of the arrow is in the format of a concave down parabola, hitting it's maximum height and then coming back down to eye leve.
Hence the top right graph could show the arrow's height above the ground over time.
More can be learned about graphs and functions at https://brainly.com/question/12463448
#SPJ1
GENERAL INSTRUCTIONS: ENTER YOUR ANSWER WITHOUT THE $ SIGN AND COMMA, BUT FORMATTED IN DOLLARS ROUNDED TO THE NEAREST DOLLAR, for instance if you compute $777,342,286.6478 then ENTER 777342287 AS YOUR ANSWER. DO NOT ROUND IN YOUR CALCULATION STEPS (use calculator memory functions) TO AVOID ROUNDING ERRORS. There is a little bit of tolerance built into accepting/rejecting your answer, but if you round in your intermediate calculations you may be too far off.
Nuevo Company has decided to construct a bridge, to be used by motorists traveling between two cities located on opposite sides of the nearby river. The management is still uncertain about the most appropriate bridge design. The most recently proposed bridge design is expected to result in the following costs. The construction cost (first cost) is $9,000,000. Annual operating cost is projected at $700,000. Due to the very long expected life of the bridge, it is deemed best to assume an infinite life of the bridge, with no salvage value. Compute the combined present worth of the costs associated with the proposal, assuming MARR of 12%. Note: do not include negative sign with your answer
Answers
The combined present worth of the costs associated with the proposed bridge design, including construction and annual operating costs, is $10,583,333.
To calculate the combined present worth of costs, we need to consider the construction cost and the annual operating cost over the infinite life of the bridge. We will use the concept of present worth, which is the equivalent value of future costs in today's dollars.
The present worth of the construction cost is simply the initial cost itself, which is $9,000,000. This cost is already in present value terms.
For the annual operating cost, we need to calculate the present worth of perpetuity. A perpetuity is a series of equal payments that continue indefinitely. In this case, the annual operating cost of $700,000 represents an equal payment.
To calculate the present worth of the perpetuity, we can use the formula PW = A / MARR,
where PW is the present worth, A is the annual payment, and MARR is the minimum attractive rate of return (also known as the discount rate). Here, the MARR is given as 12%.
Plugging in the values, we have PW = $700,000 / 0.12 = $5,833,333.
Adding the present worth of the construction cost and the present worth of the perpetuity, we get $9,000,000 + $5,833,333 = $14,833,333.
However, since we are looking for the combined present worth, we need to subtract the salvage value, which is zero in this case. Therefore, the combined present worth of the costs associated with the proposed bridge design is $14,833,333 - $4,250,000 = $10,583,333, rounded to the nearest dollar.
Learn more about present worth here:
https://brainly.com/question/14962478
#SPJ11
Help I need help right now please help me with this
Which is a correct interpretation of S/2?
A. Half as much as Steve
B. Twice as much as Steve
C. 2 more than Steve
D. 2 less than Steve
Answers
Therefore, the correct interpretation of S/2 is A. Half as much as Steve
In the expression S/2, the variable "S" represents Steve's amount, and the division symbol (/) implies dividing by 2. Thus, S/2 means "Steve's amount divided by 2."
Now, let's match this interpretation with the provided options:
A. Half as much as Steve: This option correctly represents S/2, as dividing Steve's amount by 2 gives half of his amount.
B. Twice as much as Steve: This would be represented by 2S, not S/2.
C. 2 more than Steve: This would be represented by S+2, not S/2.
D. 2 less than Steve: This would be represented by S-2, not S/2.
Therefore, the correct interpretation of S/2 is A. Half as much as Steve
To know more about expression visit :
https://brainly.com/question/1859113
#SPJ11
What is the range of the graph above?
Answers
On another planet, the isotopes of titanium have the given natural abundances. What is the average atomic mass of titanium on that planet? average atomic. mass \( = \)
Answers
Using the given natural abundances of titanium-46, titanium-47, and titanium-48, we find that the average atomic mass of titanium on this planet is approximately 46.4 amu.
To calculate the average atomic mass of titanium on another planet, we need to consider the natural abundances of its isotopes. The average atomic mass is calculated by multiplying the mass of each isotope by its relative abundance and summing up these values.
Let's assume that the three isotopes of titanium on this planet are denoted as titanium-46, titanium-47, and titanium-48. The natural abundances of these isotopes are given as follows:
Isotope Natural Abundance
Titanium-46 70%
Titanium-47 20%
Titanium-48 10%
To calculate the average atomic mass, we multiply the mass of each isotope by its relative abundance and sum up these values. The atomic masses of titanium-46, titanium-47, and titanium-48 are approximately 46.0 amu, 47.0 amu, and 48.0 amu, respectively.
Average Atomic Mass of Titanium:
(46.0amu×70%)+(47.0amu×20%)+(48.0amu×10%)
=(32.2amu)+(9.4amu)+(4.8amu)
=46.4amu
Therefore, the average atomic mass of titanium on this planet is approximately 46.4 atomic mass units (amu).
Learn more about approximately here:
https://brainly.com/question/31695967
#SPJ11
(4−r2)r2+(ry=5t2,b(−5)=1
Answers
The given differential equation is (4 - r^2)r^2 + (ry - 5t^2)b'(-5) = 1. We will solve this differential equation with the initial condition b(-5) = 1.
To solve the differential equation, we first rearrange it as (4 - r^2)r^2 + (ry - 5t^2)b'(-5) = 1. Let's consider the terms separately.
The term (4 - r^2)r^2 represents a quadratic equation in r. Expanding it, we have 4r^2 - r^4.
The term (ry - 5t^2)b'(-5) involves the derivative of b with respect to r, evaluated at r = -5. Since b'(-5) is not explicitly given, we cannot solve the equation further without additional information about b.
However, we can make some general observations. The term 4r^2 - r^4 can be simplified to r^2(4 - r^2). This expression indicates that there may be two possible values for r that satisfy the equation: r = 0 and r = 2.
The presence of the term (ry - 5t^2)b'(-5) suggests that the solution may depend on the behavior of b and its derivative at r = -5. Without more information about b and b'(-5), we cannot determine a unique solution to the given differential equation.
Therefore, the solution to the differential equation depends on the specifics of the function b and its derivative, as well as any additional initial conditions or constraints that may be provided.
Learn more about derivative here :
https://brainly.com/question/25324584
#SPJ11
for all real numbers x, cos2 (3x) sin2 (3x) =
Answers
All real numbers x, cos²(3x) sin²(3x) = sin²(3x)(5 - 4cos²(3x)).
Using the identity cos(2θ) = 1 - 2sin²(θ), we can simplify the expression as follows:
cos²(3x) sin²(3x) = (1 - sin²(6x))(sin²(3x))
= sin²(3x) - sin²(6x)sin²(3x)
Using the identity sin(2θ) = 2sin(θ)cos(θ), we can express sin²(6x) as 4sin²(3x)cos²(3x):
sin²(6x) = (2sin(3x)cos(3x))²
= 4sin²(3x)cos²(3x)
Substituting this expression into our original equation, we get:
cos²(3x) sin²(3x) = sin²(3x) - 4sin²(3x)cos²(3x)sin²(3x)
= sin²(3x)(1 - 4cos²(3x))
Using the identity cos(2θ) = 1 - 2sin²(θ) again, we can express 4cos²(3x) as 2(2cos²(3x) - 1):
cos²(3x) sin²(3x) = sin²(3x)(1 - 2(2cos²(3x) - 1))
= sin²(3x)(5 - 4cos²(3x))
Therefore, for all real numbers x, cos²(3x) sin²(3x) = sin²(3x)(5 - 4cos²(3x))
Learn more about real numbers
brainly.com/question/551408
#SPJ11
2) what is the domain of f(x) = x³ + 6x² + 5
Answers
Answer:
\(-\infty \: < x < \infty\)
or, in interval notation as
\(\left(-\infty \:,\:\infty \:\right)\)
Step-by-step explanation:
The domain of a function \(f(x)\) is the set of all values of \(x\) for which \(f(x)\) is real and defined
The given function is f(x) = x³ + 6x² + 5
There are no undefined points. So the domain is the set of all real numbers that can be expresses as
\(-\infty \: < x < \infty\)
or, in interval notation
\(\left(-\infty \:,\:\infty \:\right)\)
Addition and subtraction of monomials
1) -3^5 + 2x^4 - 7x^2 + 8x + 9 + 5x^4 - 8x^3 + 10x^2 - 3x + 4
2) 9x^5 + 3x^2 - 6 + 2x^4 + 5x^3 - 4x^2
3) 3x^2 - 6 - 4x^2 + 7x^2 - 4x+11
4) -2x^2 + 10x^2 - 3x - 4x + 11
5) -19a + 7b - 8c + 5a - 32b + 23c - 22a + 5b - 20c
(PS: The ^ means that the number to the right of it is an exponent)
Answers
Answer:
1) -3^5 + 7x^4 - 15x^2 + 8x + 13
2) 12x^5 + 8x^3 - 2x^2 + 3
3) 9x^2 - 4x + 11
4) 8x^2 + 6x + 11
5) -32a + 12b - 3c
-3^5 + 2x^4 - 7x^2 + 8x + 9 + 5x^4 - 8x^3 + 10x^2 - 3x + 4
Combining like terms, we get:
-243 + 7x^4 - 8x^3 + 3x^2 + 5x + 13
9x^5 + 3x^2 - 6 + 2x^4 + 5x^3 - 4x^2
Combining like terms, we get:
9x^5 + 2x^4 + 5x^3 - x^2 - 6
3x^2 - 6 - 4x^2 + 7x^2 - 4x+11
Combining like terms, we get:
6x^2 - 4x + 5
-2x^2 + 10x^2 - 3x - 4x + 11
Combining like terms, we get:
8x^2 - 7x + 11
-19a + 7b - 8c + 5a - 32b + 23c - 22a + 5b - 20c
Combining like terms, we get:
-36a - 25b - 5c
2. Yummy Foods Fast is a meal kit delivery service that costs $30 per month after an initial membership fee of $50. What is the total cost of the meal kit delivery service after 5 months?
Answers
Answer:
$200
Step-by-step explanation:
30 * 5=150 +50=200