Answers
Hope this helped
Related Questions
Show that w is in the subspace of R4 spanned by V1, V2, and V3, where these vectors are defined as follows. 1 -4 -9 -4 6 3 5 W= -2 - 1 - 1 -2 4 11 -8 - 15 To show that w is in the subspace, express was a linear combination of V1, V2, and V3. Select the correct answer below and, if necessary, fill in any answer boxes to complete your choice. O A. The vector w is in the subspace spanned by V1, V2, and V3. It is given by the formula w= (v1+ 2+ 3. (Simplify your answers. Type integers or fractions.) B. The vector w is not in the subspace spanned by V1, V2, and V3.
Answers
To show that w is in the subspace of R4 spanned by V1, V2, and V3, we need to find constants c1, c2, and c3 such that:
w = c1V1 + c2V2 + c3V3
We can write this as a matrix equation:
| 1 -4 -9 -4 | | c1 | | -2 |
| 6 3 5 1 | x | c2 | = | -1 |
| 2 4 11 -8 | | c3 | | -1 |
| -15 7 22 -14 | | -2 |
We can solve this system of equations using row reduction:
| 1 -4 -9 -4 | | c1 | | -2 |
| 6 3 5 1 | x | c2 | = | -1 |
| 2 4 11 -8 | | c3 | | -1 |
| -15 7 22 -14 | | -2 |
R2 = R2 - 6R1
R3 = R3 - 2R1
R4 = R4 + 15R1
| 1 -4 -9 -4 | | c1 | | -2 |
| 0 27 59 25 | x | c2 | = | 11 |
| 0 12 29 -16 | | c3 | | 3 |
| 0 -23 67 -59 | | -32 |
R4 = R4 + 23R2
| 1 -4 -9 -4 | | c1 | | -2 |
| 0 27 59 25 | x | c2 | = | 11 |
| 0 12 29 -16 | | c3 | | 3 |
| 0 0 174 -294 | | 225 |
R3 = R3 - (12/27)R2
R4 = (1/174)R4
| 1 -4 -9 -4 | | c1 | | -2 |
| 0 27 59 25 | x | c2 | = | 11 |
| 0 0 -1 22/3 | | c3 | | -13/3 |
| 0 0 1 -98/87 | | 25/58 |
R1 = R1 + 4R3
R2 = R2 - 59R3
R4 = R4 + (98/87)R3
| 1 0 -13 -10/3 | | c1 | | 21/29 |
| 0 27 0 -2119/87 | x | c2 | = | 2238/87 |
| 0 0 1 -98/87 | | c3 | | 25/58 |
| 0 0 0 1390/2391 | | 1009/2391 |
R1 = R1 + (13/1390)R4
R2 = (1/27)R2
R3 = R3 + (98/1390)R4
| 1
For more questions like vectors, visit the link below:
https://brainly.com/question/30887360
#SPJ11
For which of the following equations are x = 5 and x = -5 both solutions (a) x² - 25 (b) x-5 (c) x+5 (d) x²+25
Answers
Answer:
option (a) x*2-25
Step-by-step explanation:
With the help of the given roots of the equation, we can determine the factors of the polynomial. By multiplying the factors among themselves we will get the needed equation.
The roots are given as x = 5, x = -5.
Also the factors of the equation can be written as( x- 5) and( x 5)
On multiplying the factors among themselves we get the needed equation
Hence, the needed equation will be( x- 5) ×( x 5)
= x ²- 25
To know more about this
https://brainly.com/question/10387593
Can I please get help?

Answers
Consider the following data drawn independently from normally distributed populations: (You may find it useful to appropriate table: z table or t table)
xˉ1 = −17.1
s1^2 = 8.4
n1=22
xˉ2 = −16.0
s2^2 = 8.7
n2 = 24
a. Construct the 90% confidence interval for the difference between the population means. Assume the population va unknown but equal. (Round final answers to 2 decimal places.)
confidence interval is __ to __
Answers
The 90% confidence interval for the difference in the population means is -2.51 to 0.31
Calculating the 90% confidence interval for the population mean differenceFrom the question, we have the following parameters that can be used in our computation:
xˉ₁ = −17.1
s₁² = 8.4
n₁ = 22
xˉ₂ = −16.0
s₂² = 8.7
n₂ = 24
Calculate the pooled variance using
P = (df₁ * s₁² + df₂ * s₂²)/df
Where
df₁ = 22 - 1 = 21
df₂ = 24 - 1 = 23
df = 22 + 24 - 2 = 44
So, we have
P = (21 * 8.4 + 23 * 8.7)/44
P = 8.56
Also, we have the standard error to be
SE = √(P/n₁ + P/n₂)
So, we have
SE = √(8.56/22 + 8.56/24)
SE = 0.86
The z score at 90% CI is 1.645, and the CI is calculated as
CI = (x₁ - x₂) ± z * SE
So, we have
CI = (-17.1 + 16.0) ± 1.645 * 0.86
This gives
CI = -1.1 ± 1.41
Expand and evaluate
CI = (-2.51, 0.31)
Hence, the confidence interval is -2.51 to 0.31
Read more about confidence interval at
https://brainly.com/question/15712887
#SPJ1
find the general solution of the following problem. y ′ 2ty = 4t 3
Answers
The general solution of the differential equation y' + 2ty = 4t^3 is y = t^2 + C*e^(-t^2), where C is a constant.
To solve this differential equation, we first find the integrating factor e^(∫2t dt) = e^(t^2). Then, we multiply both sides of the equation by the integrating factor to get:
e^(t^2) y' + 2ty e^(t^2) = 4t^3 e^(t^2)
The left-hand side can be simplified using the product rule for differentiation:
(d/dt)(y e^(t^2)) = 4t^3 e^(t^2)
Integrating both sides with respect to t, we obtain:
y e^(t^2) = (t^4/2) + C
Solving for y, we get the general solution: y = t^2 + C*e^(-t^2), where C is a constant. This is the solution that satisfies the differential equation for any value of t. The constant C can be determined by specifying an initial condition, such as y(0) = 1.
Learn more about integrating factor here: brainly.com/question/8599681
#SPJ11
Plz help it is 10 points

Answers
Oh please first if the rectangle was compete, it's area would be 8.
The area of the missing triangle is \(\frac{2*2}{2}\)=2.
8-2=6
And there you go! Your answer is 6.
Find a formula for the nth term of the sequence where a_n is calculated directly from n. 5 / 1, 9 / 2, 13 / 6, 17 / 24, 21 / 120, ... a_n = for n ⥠1
Answers
The formula for the nth term of the given sequence is: a_n = (4n + 1) / (n!)
Numerators:
-The numerators of the sequence follow the pattern of 4n + 1, where n is the position of the term in the sequence. We can observe that each numerator is obtained by adding 4 to the product of n and 1.
Denominators:
-The denominators of the sequence correspond to the factorials of the corresponding n value. The denominator for each term is given by n!, where n is the position of the term.
Combining the above observations, we can express the nth term of the sequence as:
a_n = (4n + 1) / (n!)
For example:
- The numerator of the first term is 5, which is obtained by adding 4 to the product of 1 and 1, i.e., 4(1) + 1. Similarly, the numerator of the second term is 9, which is obtained by adding 4 to the product of 2 and 1, i.e., 4(2) + 1.
- The denominator of each term is the factorial of the corresponding n value, i.e., n! For example, the denominator of the third term is 6!, which is equal to 720.
- Therefore, the nth term of the sequence can be expressed as (4n + 1) / (n!).
For example, to find the 4th term of the sequence, we plug in n=4 into the formula:
a_4 = (4(4) + 1) / (4!) = 17/24
Similarly, to find the 6th term of the sequence, we plug in n=6 into the formula:
a_6 = (4(6) + 1) / (6!) = 21/120 = 7/40
Know more about the sequence click here:
https://brainly.com/question/13836396
#SPJ11
Need help kinda quick

Answers
Answer:
A;-6
B;-8
C;-2
D;-14
E;-1
F;2
G;5
H;0
Which angle is complementary to angle ?

Answers
Answer:
angle BAC is complementary to angle ACB
Step-by-step explanation:
Complementary angles add up to 90 degrees.
In a triangle, the sum of angles is 180 degrees.
ABC is a right triangle, so angles a+c=90 degrees.
Answer:
a)angle ACB
Basic facts:
angles in a triangle add up to 180
complementary angles are angles which add up to 90
Step-by-step explanation:
we can see the triangle is a right-angle triangle
if we subtract angle ABC (90 degrees)we are left with 90 degrees
therefore angle BAC and ACB add up to 90
Suppose that for a certain company, C(x) = 35x + 2500 represents the total cost function, and R(x) = 60xrepresents the total revenue function.(a) Find the total-profit function(b) Find the break-even point.(a) The total-profit function is P(x) =(Type your answer in slope-intercept form.)
Answers
Total cost function is C(x) = 35x + 2500
Total revenue function is R(x) = 60x
a)
Recall,
total profit = total revenue - total cost
Total profit function would be
P(x) = R(x) - C(x)
P(x) = 60x - (35x + 2500)
P(x) = 60x - 35x - 2500
P(x) = 25x - 2500
b) The break even point is the point where revenue - cost = 0
Revenue = cost
60x = 35x + 2500
60x - 35x = 2500
25x = 2500
x = 2500/25
x = 100
The break even occurs when x = 100
What value of a would make the graph of f(x)= ax2 open up?
A. -8
B. 0
C. 10
D. -21
Answers
Answer:
The equation is unsolvable when the 'a' variable is in it, so if we take it out, then all of them would make the equation open up.
Sorry for not giving a definite answer, but that is what I got.
Hope that this helps!
when we solve an inequality and divide by a negative. what do we need to remember to do with the inequality sign?
Answers
Answer:
To flip the sign.
Step-by-step explanation:
Whenever you divide or multiply by a negative number, you must change the direction of the sign.
Let's say we have a box with 6 marbles: 3 red, 1 blue, 1 green, and 1 yellow. What is the probability of picking a yellow marble, returning it to the box, and then picking a blue marble?
A) 1/12
B)1/30
C)1/36
D)1/11
Answers
The below dimensions represent the side measurements of triangles. Which one is not a right triangle?
A-6, 7, 8
B-3, 4, 5
C-9, 40, 41
D-16, 30, 34
Answers
Option A, with side measurements of 6, 7, and 8, is not a right triangle because it does not satisfy the Pythagorean theorem. The other options (B, C, and D) are right triangles since their side measurements satisfy the Pythagorean theorem.
To determine which triangle is not a right triangle, we need to check if the given side measurements satisfy the Pythagorean theorem, which states that in a right triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the other two sides.
Let's calculate the values for each option:
A) Using the Pythagorean theorem: 6^2 + 7^2 = 36 + 49 = 85
Since 85 is not equal to 8^2 (64), option A is not a right triangle.
B) Using the Pythagorean theorem: 3^2 + 4^2 = 9 + 16 = 25
Since 25 is equal to 5^2 (25), option B is a right triangle.
C) Using the Pythagorean theorem: 9^2 + 40^2 = 81 + 1600 = 1681
Since 1681 is equal to 41^2 (1681), option C is a right triangle.
D) Using the Pythagorean theorem: 16^2 + 30^2 = 256 + 900 = 1156
Since 1156 is equal to 34^2 (1156), option D is a right triangle.
Based on the calculations, we can conclude that option A, with side measurements of 6, 7, and 8, is not a right triangle because it does not satisfy the Pythagorean theorem. The other options (B, C, and D) are right triangles since their side measurements satisfy the Pythagorean theorem.
For more questions on triangle
https://brainly.com/question/17335144
#SPJ8
Round each decimal number to the nearest whole number. Then, select the best estimate for the addition equation 1.2 + 3.6 =
4.5
5
5.5
6

Answers
Answer:
4.5
Step-by-step explanation:
1.2 + 3.6 = 4.8 but when u do 4.8 -0.3 you will get 4.5
Answer:
It would be 5.5 or 5
(co 4) in a sample of 15 small candles, the weight is found to be 3.72 ounces with a standard deviation of 0.963 ounces. what would be the 87% confidence interval for the size of the candles?
Answers
The 87% confidence interval for the size of the candles is (3.503 ounces, 3.937 ounces).
To calculate the 87% confidence interval, follow these steps:
1. Identify the sample size (n=15), sample mean (3.72 ounces), and standard deviation (0.963 ounces).
2. Determine the critical value (z) for an 87% confidence interval using a standard normal distribution table or calculator. For an 87% CI, the critical value is approximately 1.534.
3. Calculate the standard error (SE) using the formula SE = standard deviation / sqrt(n). In this case, SE = 0.963 / sqrt(15) ≈ 0.248.
4. Multiply the critical value (z) by the standard error (SE) to find the margin of error (MOE): MOE = 1.534 * 0.248 ≈ 0.380.
5. Find the lower limit of the confidence interval by subtracting the MOE from the sample mean: 3.72 - 0.380 = 3.503 ounces.
6. Find the upper limit of the confidence interval by adding the MOE to the sample mean: 3.72 + 0.380 = 3.937 ounces.
So, the 87% confidence interval for the size of the candles is (3.503 ounces, 3.937 ounces).
To know more about confidence interval click on below link:
https://brainly.com/question/13067956#
#SPJ11
randomized hadamard transformations are orthogonal transformations. assume that the number of rows are in the powers of two.
Answers
Yes, it is true that randomized Hadamard transformations are orthogonal transformations.
The Hadamard matrix is a well-known example of an orthogonal matrix, which means that it preserves the dot product of vectors. An n x n Hadamard matrix is defined recursively as follows:
H(1) = [1]
H(n) = [H(n/2) ⊗ I(2) ; H(n/2) ⊗ H(2)]
where ⊗ denotes the Kronecker product and I(2) is the 2 x 2 identity matrix. This definition ensures that the resulting matrix has orthogonal rows and columns, and that the entries are either 1 or -1, with each row and column containing an equal number of each.
Randomized Hadamard transformations are a variant of the Hadamard transformation, where the matrix is formed by taking a random subset of the rows of the full Hadamard matrix. This subset is chosen uniformly at random, and each row is included with a probability of 1/2. The resulting matrix is also orthogonal, because it is formed by selecting a subset of the rows of an orthogonal matrix. Moreover, the properties of the Hadamard matrix ensure that the resulting matrix has fast matrix multiplication algorithms, making it useful in many applications such as signal processing and quantum computing.
It is also worth noting that the number of rows of the Hadamard matrix is always a power of two, because of the recursive definition given above. This ensures that the randomized Hadamard transformation can be efficiently computed using fast Fourier transforms or other fast algorithms that exploit the structure of powers of two.
for such more question on orthogonal transformations.
https://brainly.com/question/24400579
#SPJ11
Yes, it is true that randomized Hadamard transformations are orthogonal transformations. In fact, the Hadamard matrix itself is orthogonal, meaning that its transpose is equal to its inverse.
Randomized Hadamard transformations are created by applying a Hadamard matrix to a randomly chosen subset of rows of a larger Hadamard matrix. Since the original Hadamard matrix is orthogonal, any subset of its rows will also be orthogonal. Therefore, applying a Hadamard matrix to a random subset of rows will result in an orthogonal transformation as well. It is worth noting that this is only true if the number of rows is a power of two, as Hadamard matrices are only defined for such dimensions.
Randomized Hadamard transformations are indeed orthogonal transformations. In this context, an orthogonal transformation is a linear transformation that preserves the inner product of vectors, meaning that the transformed vectors remain orthogonal (perpendicular) to each other.
A Hadamard matrix is a square matrix whose entries are either +1 or -1, and its rows are orthogonal to each other. The Hadamard transformation is achieved by multiplying a given vector with the Hadamard matrix.
Assuming that the number of rows in the Hadamard matrix is a power of two (2^n), the randomized Hadamard transformation involves selecting a random Hadamard matrix of size 2^n x 2^n, and then applying the transformation to the given vector. Since the Hadamard matrix has orthogonal rows, the transformed vector will also be orthogonal, preserving the orthogonal property of the original vector.
In summary, randomized Hadamard transformations are orthogonal transformations that utilize Hadamard matrices with a number of rows in the powers of two.
Learn more about Hadamard Matrix here: brainly.com/question/31629623
#SPJ11
Answer the question written in the image.

Answers
Answer: 28
Step-by-step explanation:
The pattern is multiply the right and bottom, add the left
For example, 9*8+7=79
So, 24*3+x=100
72+x=100
x=28
4d + 5 - 9d + 2 = 13
Answers
Answer: d = -1.2
Step-by-step explanation: First you combine like terms. You add 5 +2 which gives you 7, and then you subtract 9 from 5 which gives you -5d. Then you subtract 7 from 13 which gives you 6. Divide both sides by -5 and you get -1.2. Always make sure to check your answer by plugging your answer into the place of the d variable
Li tried to evaluate an expression step by step. Find Li's mistake. What is the mistake he made. Is it A:step 1, B:step 2, C:step 3 or D: Li did not make a mistake ???


Answers
Answer: C Step 3
Step-by-step explanation: I passed
THANK YOU FOR THE OTHER BUT THIS IS THE LAST ONE MANY THANKS
5(2y-4)+5(2y-2)
Answers
Answer: 20y - 30
Step-by-step explanation:
distribute, then combine like terms.
A school knows that 10% of its students are left-handed. What is the
probability that there will be between 33 and 45 left-handed students in a
randomly selected group of 400? Use your calculator and this formula: Plasx
sb) = binomcdf(n,p.b) - binomcdf(n,p,a - 1). Round your answer to three
decimal places.
A. 0.821
B. 0.103
C. 0.718
D. 0.138
Answers
The probability that there will be between 33 and 45 left-handed students in a randomly selected group of 400 from a school where 10% of the students are left-handed is 0.718.
To solve this problem, we can use the binomial distribution formula, which gives the probability of getting exactly x successes in n independent trials, where each trial has a probability of p of being a success. In this case, we want to find the probability of getting between 33 and 45 left-handed students in a group of 400, where the probability of a student being left-handed is p = 0.10.
Using the binomcdf formula, we can find the cumulative probability of getting between 0 and 32 left-handed students and subtract it from the cumulative probability of getting between 0 and 45 left-handed students. That is, we want to find:
P(33 ≤ x ≤ 45) = binomcdf(400, 0.10, 45) - binomcdf(400, 0.10, 32-1)
Using a calculator, we find that P(33 ≤ x ≤ 45) is approximately 0.718 when rounded to three decimal places. Therefore, the answer is (C) 0.718.
Learn more about probability here
https://brainly.com/question/13604758
#SPJ11
8 The table shows number of bottles of water four
students drank. One bottle holds 335 milliliters. How
many more fluid ounces did Michael drink than
Lydia? (Hint: 1 fl oz ≈ 30 mL)
Kyle = 5 Bottles of Water
Lisa = 4 Bottles of Water
Lydia = 3 Bottles of Water
Michael = 6 Bottles of Water

Answers
Michael drinks 33.5 fl oz more fluid ounces than Lydia.
Given in question,
30 ml = 1 fl oz
1 ml = 1/30 fl oz
1 bottle = 335 milliliters
No. of bottles of water Michael drank = 6
= 6 * 335 milliliters
= 2010 milliliters
= 2010/30 fl oz
= 67 fl oz
No. of bottles of water Lydia drank = 3
= 3 * 335 milliliters
= 1005 milliliters
= 1005/30 fl oz
= 33.5 fl oz
Therefore, 67 - 33.5 = 33.5
Hence, Michael drinks 33.5 fl oz more fluid ounces than Lydia.
To learn more about fluid ounces here:
https://brainly.com/question/8500307
#SPJ1
The following system of linear equations is shown in the graph.
y=1/4x+5
x-4y=4
How many solutions does the system of linear equations have?
A. No solution
B. Infinitely many solutions
C. One solution at (4,0)
D. One solution at (0,-1)

Answers
Answer:
Step-by-step explanation:
The slopes of both those lines are the same so there is no solution. Use slope triangles to find out the slope. They are both 1/4.
A. No solution
y = 1/4x+5
x - 4y = 4
You can simplify the second equation into y = 1/4x - 1
Since these equations both have the same slope, they are parallel. When two lines are parallel, they have no solutions.
Point `A` is located at coordinates `(-3,\ 2)`.
(b) Point `C` is the image of point `A` after a translation `2` units to the right, and then a reflection across the `x`-axis. What are the coordinates of point `C`?
Answers
The coordinates for point C are mathematically given as
(x,y)= (-2, 3).
This is further explained below.
What are coordinates?Generally, A coordinate system is a system that makes use of one or more integers, also known as coordinates, in order to precisely identify the location of points or other geometric components on a manifold, such as Euclidean space.
In conclusion, The mathematical expression for the coordinates of point C is written as (x,y)=.(-2, 3).
Read more about coordinates
https://brainly.com/question/7869125
#SPJ1
Mariana made a quilt square with the design shown below.
https://cdn.app.edmentum.com/EdAssets/cfa811cb5c44407fbc5e76dd7dfc22a8?ts=635545793215170000
Which of the following best describes the shaded triangle with the given measures?
A.
obtuse isosceles triangle
B.
right scalene triangle
C.
obtuse scalene triangle
D.
right isosceles triangle
Answers
Answer:
B.
right scalene triangle
Step-by-step explanation:
how do you factor 20x^5+54x^4+10x^3
Answers
Answer:
2x^3(5x + 1) (2x + 5)
Step-by-step explanation:
I used a website called math.way, u should try it too!
If one inch represents 12 feet what dimension would you use to make a scale drawing of a building 75 feet by 80 feet?
Answers
6.25 inch by 20/3 inch (6.67 inch).
Explanation:
Use the scale as a conversion factor.
Scale: 1 inch = 12 feet
Conversion factor: by the division property of equaltiy you can divide each side by 12 feet
1 inch / 12 feet = 1
Convert 75 feet:
75 feet × 1 inch / 12 feet = 6.25 inch
Convert 80 feet:
80 feet × 1 inch / 12 feet = 20/3 inch ≈ 6.67 inch
Thus, the dimesions to make a scales drawing of 75 feet by 80 feet are 6.25 inch and 20/3 inch (6.67 inch).
Answer:
6.25 inch by 20/3 inch (6.67 inch).
Explanation:
Use the scale as a conversion factor.
Scale: 1 inch = 12 feet
Conversion factor: by the division property of equaltiy you can divide each side by 12 feet
1 inch / 12 feet = 1
Convert 75 feet:
75 feet × 1 inch / 12 feet = 6.25 inch
Convert 80 feet:
80 feet × 1 inch / 12 feet = 20/3 inch ≈ 6.67 inch
Thus, the dimesions to make a scales drawing of 75 feet by 80 feet are 6.25 inch and 20/3 inch (6.67 inch).
does (3,-4) lies on the locus x2+y2=25
Answers
Answer:
Yes
Step-by-step explanation:
Both arguments are squared so the equation are in the form of a circle.
A lotus is a point that is equidistant from some fixed point of a conic section. This is a circle so the fixed point is called a center of the circle.
The center of the circle is equidistant from any point on the circumference of the circle. In order for a point to be on the circle, it must satisfy the circle equation.
\( {x}^{2} + {y}^{2} = {r}^{2} \)
Let plug in what we know
\(3 {}^{2} + ( - 4) {}^{2} = {5}^{2} \)
\(9 + 16 = {5}^{2} \)
So 3,-4 is on the locus of the circle.
Find the lateral surface area of the figure.
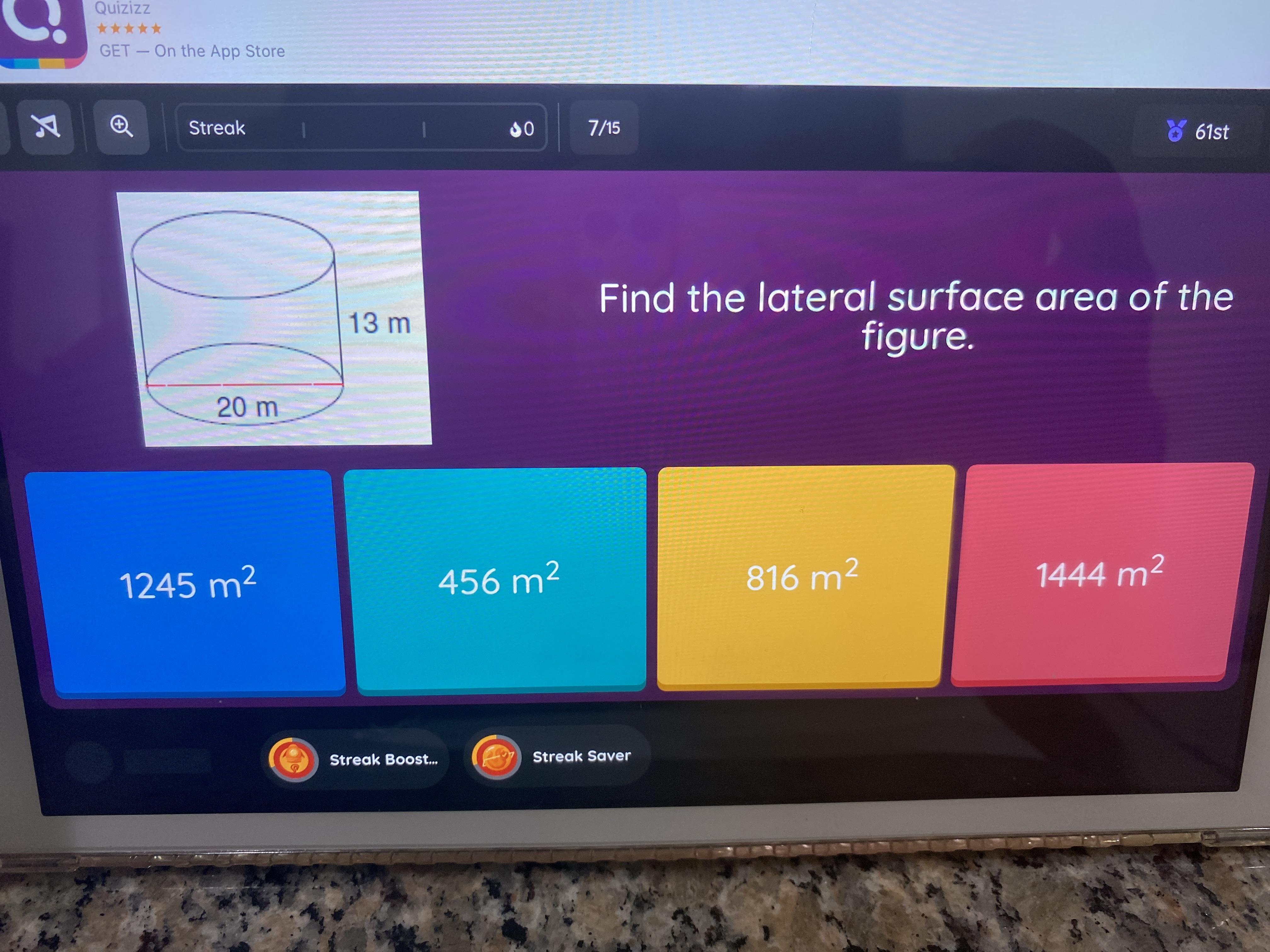
Answers
The evaluated lateral surface area is 261.8 square meters, under the condition that the base length is 20 m and height is 13 m.
The lateral surface area of a cylinder is given by the formula 2πrh
Here,
r = radius of the base
h = height of the cylinder.
For the given case, the base length is 20 m and height is 13 m. Then the base length is stated instead of the radius, we have to evaluate the radius first.
The radius of a cylinder can be found applying the formula r = l/2π
Here,
l = base length.
So, staging l = 20 m
, we get
r = 20/(2π)
≈ 3.18 m
Now that we have received the radius and height, we can evaluate the lateral surface area applying the formula mentioned above.
Staging
r = 3.18 m
h = 13 m,
we get:
Lateral surface area
= 2πrh
≈ 261.8 m²
Then, the lateral surface area of the given cylinder is approximately 261.8 square meters.
To learn more about surface area
https://brainly.com/question/951562
#SPJ1
