Answers
Answer:
i think its c. srry if im wrong
Step-by-step explanation:
Answer:
A = 8
Step-by-step explanation:
For the equation to have infinitely many solutions , then the terms on both sides must be the same.
Qw require the x- terms on the right side to be 6x
Ax - 2x = 6x ( consider the coefficients )
A - 2 = 6 ( add 2 to both sides )
A = 8
Related Questions
if t+t = 0
what is the answer
Answers
Answer:
t = 0
Step-by-step explanation:
t + t = 0 , that is
2t = 0 ( isolate t by dividing both sides by 2 )
t = \(\frac{0}{2}\) = 0
Answer:
t=0
Step-by-step explanation:
t+t is 0 and since were not given any numbers for t its automatically 0
how much space is shown in the circle below
Answers
Answer:
there is no circle! maybe you forgot to attach it?
Note:
Please mark as Brainliest! <3
for geometry:(
will give brainist
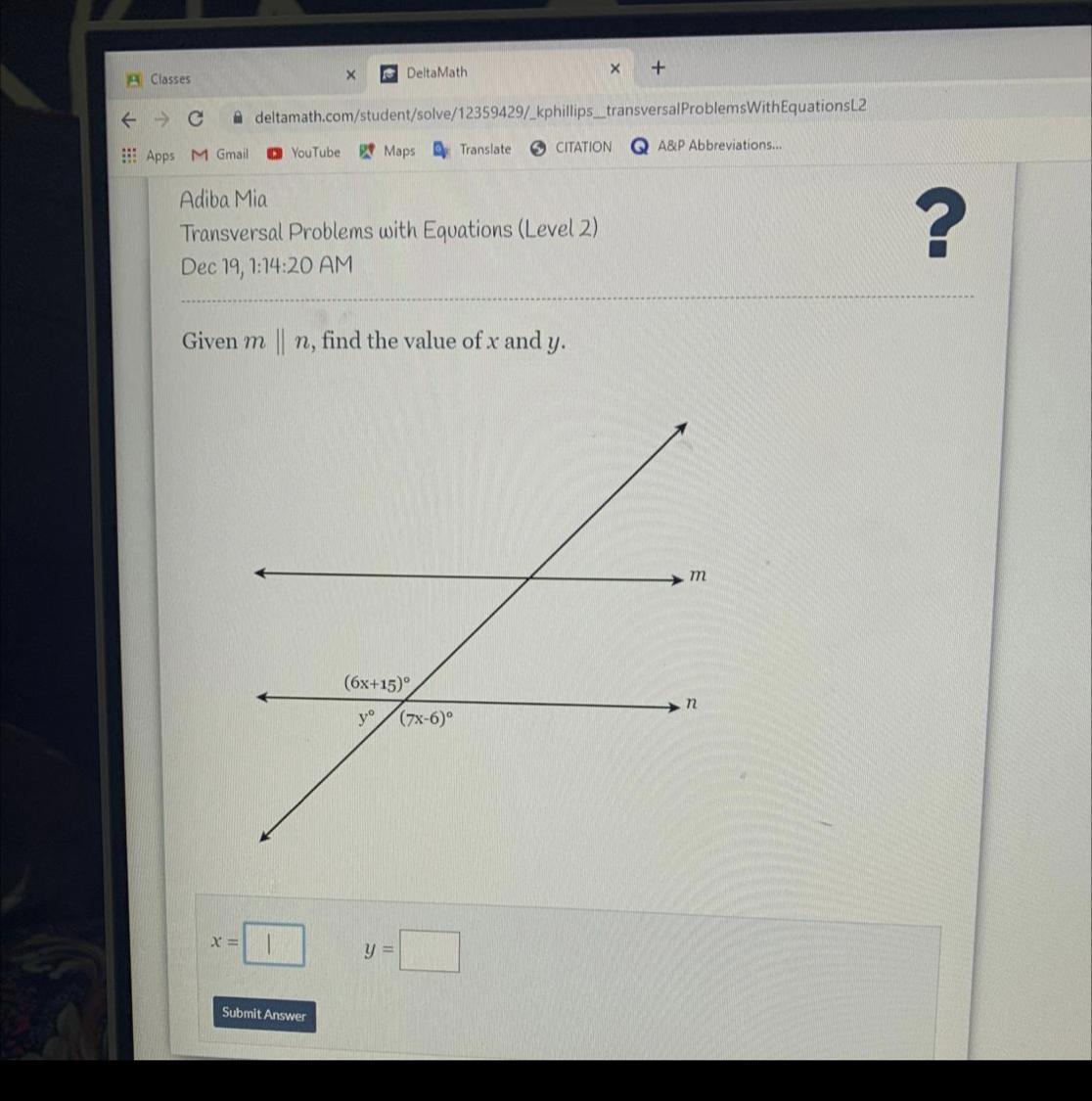
Answers
Y= 39
Why?
(6x+15) = (7x-15) solve and get 21 then
7*21-15= 141 take 141 and subtract 180
180-141= 39
Hope this Helps :D
Answer:
x=21,y=159
Step-by-step explanation:
6x+15=7x-6 ( vertically opposite angles)
x=21°
21°+y = 180° (straight angle)
Peter can mow his lawn in 6 minutes. Peter's son can mow it in 8 minutes. How long will it take them to do it together?
Answers
Answer:
3 minutes 26 seconds
Step-by-step explanation:
rate x time in Distance problems, and W = rate x time in work problems. The Work is generally 1, the whole job.
For Peter the formula is 1 (lawn mowed) = 1/6 lawn per minute x 6 minutes.
For the son the formula is 1 = 1/8 * 8.
Add their rates together, 1/8 + 1/6 = 3/24 + 4/24 = 7/24.
The equation for their rate working together is 1 = 7/24 * t
Divide both sides by 7/24 to find t. t = 1 / 7/24 = 1 * 24/7 = 24/7 = 3 and 3/7 minutes = approx. 3 minutes 26 seconds.
8 - 8,16,24,32,40,48,56,64,72,80
Answer should be 24 minutes.
what sign can i use for division
Answers
let a and b be n × n matrices such that ab = in . prove that the rank of a is n
Answers
The rank of matrix A is n.
To prove that the rank of matrix A is n, we'll use the facts that AB = I_n (the n x n identity matrix) and that the rank of a product of matrices is less than or equal to the minimum of the ranks of the individual matrices. Here's a step-by-step explanation:
1. Given: A and B are n x n matrices such that AB = I_n.
2. Let's denote the rank of A as rank(A) and the rank of B as rank(B).
3. Since AB = I_n, it's clear that the product of matrices A and B results in the identity matrix, which has a rank of n (rank(I_n) = n).
4. According to the properties of matrix ranks, rank(AB) ≤ min(rank(A), rank(B)).
5. As AB = I_n, we have rank(I_n) ≤ min(rank(A), rank(B)).
6. Since the rank of the identity matrix is n, we have n ≤ min(rank(A), rank(B)).
7. As A and B are n x n matrices, their maximum possible rank is n, so rank(A) ≤ n and rank(B) ≤ n.
8. From step 6, we know that n ≤ rank(A). Combining this with rank(A) ≤ n, we conclude that rank(A) = n.
Therefore, the rank of matrix A is n.
Learn more about rank of matrix here: brainly.com/question/29811883
#SPJ11
ASAP
“A map uses the scale 3 of an inch represents 3/4 miles. If the actual distance between two cities is
25 miles, then what is the length on the map?”
Answers
Answer:
3 = 3/4
but 3/4= 0.75
3 = 0.75
x = 25
cross multiply
0.75x = 75
divide both sides by 0.75
x = 100
therefore 25miles represent 100inch on a map
PLEASE! HELP HELP HELP!
Answers
Answer:
it's say download FPD SORRY I CAN'T SLOVE IT
what is 63 divided by 9
Answers
Answer:
7
Step-by-step explanation:
Answer:
7
Step-by-step explanation:
9 / 63
- 0
----------
63
- 63
----------
0
Hope this helped :)
Maria was given this absolute value graph and needs to come up with the equation, domain, range and intercepts.
function is y = |x|..and from her knowledge with translations she knows that it has translated horizontally to the right 4 units.
So she says the new equation must be y = |x+4|. The domain is all values of x. The range is all values of y greater u
to zero. The y-intercept is (0,4). There isn't an x intercept, because it just sits at (4,0). can you find any errors in her solution?

Answers
Maria wrote incorrectly the function, it is:
y = |x - 4|
And:
Domain: all real numbers.Range: all real numbers equal to or larger than zero.y-intercept: (0, 4)x-intercept: (4, 0).There are errors in her solution?She started with the parent absolute value function:
y = |x|
And wrote a translation to the right as:
y = |x + 4|
That is her mistake, a translation to the right of N units is written as:
g(x)= f(x - N)
So for a translation to the right of 4 units, we need to subtract 4 to the input, the actual function that we can see on the graph is written as:
y = |x - 4|
Now, the y-intercept is what we get when we evaluate in x = 0:
y = |0 - 4| = 4
So the y-intercept is (0, 4).
The x-intercept is the value of x such that y = 0, so we need to solve:
|x - 4| = 0
x - 4 = 0
x = 4
The x-intercept is (4, 0).
Finally, the domain (like in all absolute value functions) is the set of all real numbers, and the range is the set of all real numbers equal to or larger than zero.
Learn more about absolute value functions:
https://brainly.com/question/3381225
#SPJ1
-25 x(84/21)+(-3)x(-6)
Answers
To solve the expression -25 x (84/21) + (-3) x (-6), follow these steps:
Step 1: Perform the division inside the parentheses.
(84/21) = 4
Step 2: Replace the terms and rewrite the expression.
-25 x (4) + (-3) x (-6)
Step 3: Perform the multiplications.
-25 x 4 = -100
-3 x -6 = 18
Step 4: Rewrite the expression and perform the addition.
-100 + 18
Step 5: Calculate the final result.
-100 + 18 = -82
Your answer is -82.
To learn more about expression : brainly.com/question/14083225
#SPJ11
Find the Fare without Tip: 3 passengers, 9.5 miles.
O $19.54
O$16.70
O $18.29
O$17.48

Answers
Answer:
$16.70
Step-by-step explanation:
9.5 miles / .25 = 38
The first mile is 1.25 so we do this
37 * .35 = 12.95
12.95 + 1.25 = 14.2
14.2 + 1.25 + 1.25(two additional passengers) = 16.70
QUESTION IN THE ATTACHMENT

Answers
Answer:
A. The sum of the first 10th term is 100.
B. The sum of the nth term is n²
Step-by-step explanation:
Data obtained from the question include:
Sum of 20th term (S20) = 400
Sum of 40th term (S40) = 1600
Sum of 10th term (S10) =..?
Sum of nth term (Sn) =..?
Recall:
Sn = n/2[2a + (n – 1)d]
Sn is the sum of the nth term.
n is the number of term.
a is the first term.
d is the common difference
We'll begin by calculating the first term and the common difference. This is illustrated below:
Sn = n/2 [2a + (n – 1)d]
S20 = 20/2 [2a + (20 – 1)d]
S20= 10 [2a + 19d]
S20 = 20a + 190d
But:
S20 = 400
400 = 20a + 190d .......(1)
S40 = 40/2 [2a + (40 – 1)d]
S40 = 20 [2a + 39d]
S40 = 40a + 780d
But
S40 = 1600
1600 = 40a + 780d....... (2)
400 = 20a + 190d .......(1)
1600 = 40a + 780d....... (2)
Solve by elimination method
Multiply equation 1 by 40 and multiply equation 2 by 20 as shown below:
40 x equation 1:
40 x (400 = 20a + 190d)
16000 = 800a + 7600. ........ (3)
20 x equation 2:
20 x (1600 = 40a + 780d)
32000 = 800a + 15600d......... (4)
Subtract equation 3 from equation 4
Equation 4 – Equation 3
32000 = 800a + 15600d
– 16000 = 800a + 7600d
16000 = 8000d
Divide both side by 8000
d = 16000/8000
d = 2
Substituting the value of d into equation 1
400 = 20a + 190d
d = 2
400 = 20a + (190 x 2)
400 = 20a + 380
Collect like terms
400 – 380 = 20a
20 = 20a
Divide both side by 20
a = 20/20
a = 1
Therefore,
First term (a) = 1.
Common difference (d) = 2.
A. Determination of the sum of the 10th term.
First term (a) = 1.
Common difference (d) = 2
Number of term (n) = 10
Sum of 10th term (S10) =..?
Sn = n/2 [2a + (n – 1)d]
S10 = 10/2 [2x1 + (10 – 1)2]
S10 = 5 [2 + 9x2]
S10 = 5 [2 + 18]
S10 = 5 x 20
S10 = 100
Therefore, the sum of the first 10th term is 100.
B. Determination of the sum of the nth term.
First term (a) = 1.
Common difference (d) = 2
Sum of nth term (Sn) =..?
Sn = n/2 [2a + (n – 1)d]
Sn = n/2 [2x1 + (n – 1)2]
Sn = n/2 [2 + 2n – 2]
Sn = n/2 [2 – 2 + 2n ]
Sn = n/2 [ 2n ]
Sn = n²
Therefore, the sum of the nth term is n²
Find the missing side in each triangle using any method.
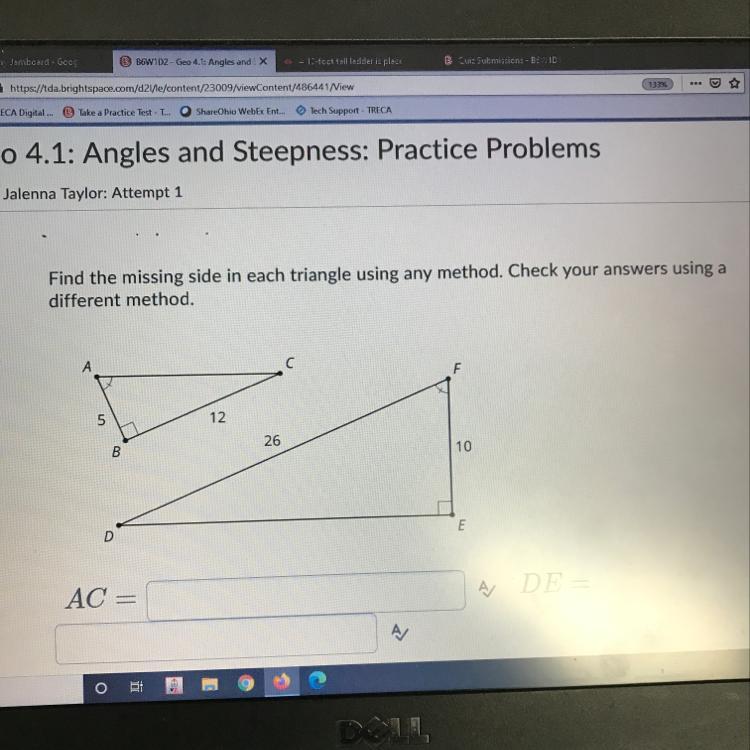
Answers
The missing side lengths of the right triangles are AC = 13 and DE = 24.
What is the Pythagorean theorem?In a right-angled triangle, the square of the hypotenuse side is equal to the sum of the squares of the other two sides, according to Pythagoras's Theorem.
Given the two right triangles.
The hypotenuse of the first right triangle is given by:
AC² = 5² + 12²
AC² = 25 + 144
AC² = 169
AC = 13
The length of the leg in the second triangle is given by:
DE² = 26² - 10²
DE² = 676 - 100
DE² = 576
DE = 24
Hence, the missing side lengths of the right triangles are AC = 13 and
DE = 24.
Learn more about Pythagorean thoerem:
https://brainly.com/question/16307146
#SPJ2
System of differential equations, where p, q ≥ 0: p′ =p(1−p−q) q′ =q(2−3p−q)(a) Construct the phase plane, plotting all nullclines, labeling all equilibria, and indicating the direction of motion. (b) Obtain an expression for each equilibrium
Answers
The equilibrium E2 corresponds to a stationary point where p increases (p' > 0) and q does not change (q' = 0).
To construct the phase plane for the given system of differential equations, we first need to find the nullclines and identify the equilibria.
(a) Nullclines and Equilibria:
For the first equation, p' = p(1 - p - q), we set p' = 0 and solve for p:
p(1 - p - q) = 0
This equation has two solutions:
p = 0
1 - p - q = 0
For the second equation, q' = q(2 - 3p - q), we set q' = 0 and solve for q:
q(2 - 3p - q) = 0
This equation also has two solutions:
q = 0
2 - 3p - q = 0
Now we can plot the nullclines on the phase plane:
Nullcline for p' = 0: p = 0 (horizontal line)
Nullcline for 1 - p - q = 0: q = 1 - p (diagonal line)
Nullcline for q' = 0: q = 0 (vertical line)
Nullcline for 2 - 3p - q = 0: q = 2 - 3p (diagonal line)
Next, we identify the equilibria by solving the equations:
Equilibrium for p = 0 and q = 1 - p: p = 0, q = 1 (Equilibrium E1)
Equilibrium for q = 0 and 2 - 3p - q = 0: p = 2/3, q = 0 (Equilibrium E2)
Now we can plot the equilibria on the phase plane.
To indicate the direction of motion, we can choose a few points in different regions of the phase plane and evaluate p' and q' at those points. This will help us determine the direction of the vector field arrows.
(b) Expression for each equilibrium:
For Equilibrium E1: p = 0, q = 1
Substituting these values into the given system of differential equations:
p' = 0(1 - 0 - 1) = 0
q' = 1(2 - 3(0) - 1) = 1
The equilibrium E1 corresponds to a stationary point where p does not change (p' = 0) and q increases (q' > 0).
For Equilibrium E2: p = 2/3, q = 0
Substituting these values into the given system of differential equations:
p' = (2/3)(1 - 2/3 - 0) = 2/9
q' = 0(2 - 3(2/3) - 0) = 0
Know more about differential equations here:
https://brainly.com/question/25731911
#SPJ11
write (14+x)+(12x-8) in standard form
Answers
Answer:
13x+6
Step-by-step explanation:
help plz, lotta points

Answers
Answer:
im confused
Step-by-step explanation:
Identify the characters of series below. nvž enn |||-) En=12 100 1-) Σπίο 3* 2"-1 ||-) En=2 n A) I Convergent, II Divergent, III Convergent B) I Convergent, Il Convergent, III Divergent C) I Convergent, II Convergent, III Convergent D) I Divergent, Il Divergent, III Divergent E) I Divergent, II Divergent, III Convergent
Answers
Based on the information, we can determine convergence or divergence of series.The given options do not provide a clear representation of potential outcomes.It is not possible to select correct option.
The given series is "nvž enn |||-) En=12 100 1-) Σπίο 3* 2"-1 ||-) En=2 n". In the series, we have the characters "nvž enn |||-)" which indicate the series notation. The characters "En=12 100 1-" suggest that there is a summation of terms starting from n = 12, with 100 as the first term and a common difference of 1. The characters "Σπίο 3* 2"-1 ||-) En=2 n" indicate another summation, starting from n = 2, with a pattern involving the operation of multiplying the previous term by 3 and subtracting 1.
To learn more about convergence click here : brainly.com/question/32549533
#SPJ11
A. the function has a maximum value of 1
B.the function has a minimum value of 1
C.the function has a maximum value of -2
D.the function has a minimum value of -2

Answers
Answer:
A) The function has a maximum value of 1
Step-by-step explanation:
Since the parabola opens downward, then its maximum would be 1 and its minimum would be -∞
what is the value of this

Answers
Answer:
Answer is 24
Step-by-step explanation:
Because of z is 6
6 x 6 = 36
2² = 4
36 ÷ 4 = 9
5 x 3 = 15
15 + 9 = 24
This shows a figure. What is the measure of angle MRX?
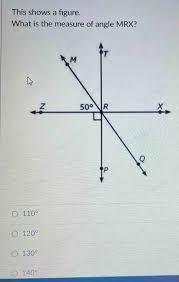
Answers
The measurement of the angle MRX is 130°.
Given that a figure we need to find the angle MRX,
The lines TP and ZX are perpendicular to each other, and there is a line MQ intersecting at R,
So,
Angles MRT and MRZ are complementary so,
m ∠MRZ + m ∠MRT = 90°
50° + m ∠MRT = 90°
m ∠MRT = 40°
Also,
Angles TRX and TRZ are supplementary so, and equal to right angle, so,
m ∠MRX = m ∠MRT + m ∠TRX
m ∠MRX = 90° + 40°
m ∠MRX = 130°
Hence the measurement of the angle MRX is 130°.
Learn more about supplementary and complementary angles click;
https://brainly.com/question/31132454
#SPJ1
if a pack of 50 pencils cost $5.45 how much does a single pencil cost
Answers
If a pack of 50 pencils cost $5.45 then a single pencil costs $0.109.
What is ratio?Ratio basically compares quantities, that means it shows the value of one quantity with respect to the other quantity.
If a and b are two values, their ratio will be a:b,
Given that,
Cost of a pack of 50 pencils = $5.45.
To find the cost of one pencil,
Use ratio property,
50 pencil costs = $5.45
1 pencil costs = 5.45 / 50 = $0.109
Cost of one pencil is $0.109.
To learn more about Ratio on :
https://brainly.com/question/13419413
#SPJ5
If 60% of a given number is 18.0, what is 25% of
the given number?
Answers
Step-by-step explanation:
Let the number be x
From the question 60% of the number is 18
The equation is
\( \frac{60}{100} x = 18\)
Multiply through by 100
That's
\(100 \times \frac{60}{100} x = 18 \times 100 \\ 60x = 1800 \\ \frac{60x}{60} = \frac{1800}{60} \)
We have the final answer as
x = 30The number is 3025% of the number is
\( \frac{25}{100} \times 30 \\ \rarr \: \frac{1}{4} \times 30 \\ \rarr \: \frac{30}{4} \: \: \: \: \: \: \: \\ \rarr \: \: \: \: \frac{15}{2} \)
We have the final answer as
7.5Hope this helps you
1.) Shown is Equilateral triangle ABC.
AB = 6 cm.
BC
11
CA E
В

Answers
Answer: All answers are 6.
Step-by-step explanation: Equilateral triangles have equal side lengths and angle measures.
Answer:
Step-by-step explanation:
All sides of an equilateral triangle is equal.so,
length BC=6 cm
length CA=6 cm
A used car dealer gets complaints about his cars as shown in the table
Number of complaints per day 0 1 2 3 4 5 6
Probability 0.01 0.08 0.11 0.24 0.36 0.11 0.09
The expected number of complaints per day are ?
Answers
The expected number of complaints per day can be calculated by multiplying each number of complaints by its corresponding probability and summing up the results.
To calculate the expected number of complaints per day, we multiply each number of complaints by its respective probability and then sum up the products. Using the given table, we perform the following calculations:
Expected number of complaints = (0 * 0.01) + (1 * 0.08) + (2 * 0.11) + (3 * 0.24) + (4 * 0.36) + (5 * 0.11) + (6 * 0.09)
= 0 + 0.08 + 0.22 + 0.72 + 1.44 + 0.55 + 0.54
= 4.55
Therefore, the expected number of complaints per day is 4.55.
This means that, on average, the used car dealer can expect to receive approximately 4.55 complaints per day based on the given probabilities. It provides an estimate of the average number of complaints the dealer is likely to encounter daily.
To learn more about probability click here: brainly.com/question/30881224
#SPJ11
Consider the solid obtained by rotating the region bounded by the given curves about the line x = -4.
\ldots y=x^{\wedge} 2 \operatorname{text}(,) x=y^{\wedge} 2
Find the volume V of this solid.
Answers
The volume of the solid obtained by rotating the region bounded by \(y=x^2\) and \(x=y^2\) about \(x=-4\) is approximately \(-\frac{10\pi}{3}\) cubic units.
To find the volume of the solid obtained by rotating the region bounded by the curves \(y = x^2\) and \(x = y^2\) about the line \(x = -4\), we can use the method of cylindrical shells.
First, let's sketch the region to visualize it better. The curves intersect at two points: \((-1,1)\) and \((0,0)\). The region is symmetric with respect to the line \(y = x\), and the rotation axis \(x = -4\) is located to the left of the region.
To set up the integral for the volume, we consider an infinitesimally thin strip of height \(dy\) along the y-axis.
The radius of this strip is \(r = (-4) - y = -4 - y\), and the corresponding infinitesimal volume element is \(dV = 2\pi r \cdot y \, dy\). The factor of \(2\pi\) accounts for the cylindrical shape.
Integrating this expression from \(y = 0\) to \(y = 1\) (the y-coordinate bounds of the region), we get:
\[V = \int_0^1 2\pi (-4 - y) \cdot y \, dy\]
Evaluating this integral gives us the volume \(V\) of the solid obtained by rotating the region bounded by the given curves about the line \(x = -4\).
Certainly! Let's calculate the volume of the solid step by step.
We have the integral expression for the volume:
\[V = \int_0^1 2\pi (-4 - y) \cdot y \, dy\]
To evaluate this integral, we expand and simplify the expression inside the integral:
\[V = \int_0^1 (-8\pi y - 2\pi y^2) \, dy\]
Now, we can integrate term by term:
\[V = -8\pi \int_0^1 y \, dy - 2\pi \int_0^1 y^2 \, dy\]
Integrating, we have:
\[V = -8\pi \left[\frac{y^2}{2}\right]_0^1 - 2\pi \left[\frac{y^3}{3}\right]_0^1\]
Evaluating the limits, we get:
\[V = -8\pi \left(\frac{1^2}{2} - \frac{0^2}{2}\right) - 2\pi \left(\frac{1^3}{3} - \frac{0^3}{3}\right)\]
Simplifying further:
\[V = -8\pi \cdot \frac{1}{2} - 2\pi \cdot \frac{1}{3}\]
\[V = -4\pi - \frac{2\pi}{3}\]
Finally, combining like terms, we get the volume of the solid:
\[V = -\frac{10\pi}{3}\]
Therefore, the volume of the solid obtained by rotating the region bounded by the curves \(y = x^2\) and \(x = y^2\) about the line \(x = -4\) is \(-\frac{10\pi}{3}\) (approximately -10.47 cubic units).
Learn more about Integration click here :brainly.com/question/17433118
#SPJ11
Assuming the model remains accurate, estimate the death rate in 2029. (round to the nearest tenth.)
Answers
a) the exponential model for the data is D(t) = 248.2 * e^(-0.0337t).
b) The estimated death rate in 2025 is approximately 116.2 per 100,000 Americans.
a) To find the exponential model for the given data, we can use the formula:
D(t) = D₀ * e^(kt),
where D(t) is the death rate at time t, D₀ is the initial death rate, e is the base of the natural logarithm, k is the growth/decay constant, and t is the time elapsed.
We are given the following data points:
t = 0 (1998), D₀ = 248.2
t = 6 (2004), D(6) = 213.2
Substituting these values into the equation, we get:
213.2 = 248.2 * e^(6k).
Dividing both sides by 248.2 and taking the natural logarithm, we have:
ln(213.2/248.2) = 6k.
Solving for k, we find:
k = ln(213.2/248.2) / 6.
b) To estimate the death rate in 2025 (t = 27), we use the exponential model:
D(27) = D₀ * e^(kt).
Substituting the known values, we have:
D(27) = 248.2 * e^(ln(213.2/248.2) / 6 * 27).
Calculating this expression will give us the estimated death rate in 2025.
Performing the calculations, we find:
k ≈ -0.0476 (rounded to four decimal places)
D(27) ≈ 248.2 * e^(-0.0476 * 27) ≈ 116.2 (rounded to the nearest tenth)
for such more question on exponential model
https://brainly.com/question/30493676
#SPJ8
Question
In the year 1998, the age-adjusted death rate per 100,000 Americans from heart disease was 248.2. In the year 2004, the age-adjusted death rate per 100,000 Americans for heart disease had changed to 213.2.
a) Find an exponential model for this data, where t=0 corresponds to 1998.
b) Assuming the model remains accurate, estimate the death rate in 2025. (Round to the nearest tenth.)
One of the legs of a right triangle measures 1 cm and its hypotenuse measures 4 cm. Find the measure of the other leg. If necessary, round to the nearest tenth.
Answers
Answer:
3.9 cm
Step-by-step explanation:
One of the legs of a right triangle measures 1 cm and its hypotenuse measures 4 cm. Find the measure of the other leg. If necessary, round to the nearest tenth.
We can solve the above question using Pythagoras Theorem
Hypotenuse ² = Opposite ² + Adjacent ²
From the above question
Hypotenuse = 4 cm
1 leg = Opposite = 1 cm
Other leg = Adjacent = x
Hence
4² = 1 ² + x²
x² = 4² - 1²
x = √ 16 - 1
x = √15
x = 3.8729833462 cm
Approximately to the nearest tenth = 3.9 cm
The measure of the other leg is 3.9 cm
A broken rectangular shape window is being replaced it measures 24in by 18 inches how many square inches of glass are needed to repair the window
Answers
The number of square inches of glass are needed to repair the window is 432 square inches
How to determine the number of square inches of glass are needed to repair the window?The given parameters are:
Length = 24 inches
Width = 18 inches
The number of square inches of glass are needed to repair the window is calculated as:
Area = Length * Width
So, we have
Area = 24 inches * 18 inches
Evaluate the product
Area = 432 square inches
Hence, the number of square inches of glass are needed to repair the window is 432 square inches
Read more about area at:
https://brainly.com/question/25292087
#SPJ1
Grapes are 3.88 per pound. Marco buys 1.89
pounds. What is the total cost of his purchase?
Answers
Answer:
7.3332
Step-by-step explanation:
3.88 ⋅ 1.89 = 7.3332
