Amanda's family is taking a road trip. Their car can travel no more than 352 miles without needing to refill the gas tank. They have traveled 108 miles since they last filled the gas tank.
Amanda knows that the inequality representing this situation is 108+x≤352.
Select from the drop-down menu to correctly interpret the solution of this inequality.
Amanda's family can drive miles before they need to refill the gas tank.
Answers
From the solution to the inequality, the correct interpretation is that:
Amanda's family can drive 244 miles before they need to refill the gas tank.
The amount of miles they can still travel is modeled by the following inequality:
\(108 + x \leq 352\)
It is solved similarly to an equality, hence:
\(x \leq 352 - 108\)
\(x \leq 244\)
Then:
Amanda's family can drive 244 miles before they need to refill the gas tank.
You can learn more about inequalities at https://brainly.com/question/25629776
Answer:
hope this helps!
I choose the wrong answer lol

Related Questions
11. What is the difference between a theorem and a postulate?
Answers
Answer:
A postulate is a statement that is assumed to be true based on basic geometric principles. A theorem is a mathematical statement that can and must be proven to be true.
Step-by-step explanation:
www.ck12.org
Answer:
A thorem is true and can be proven true vs a postulate is guessed true without any evidence.
Step-by-step explanation:
A theorem is a group of statements that are used to prove something else, whereas a postulate is a statement that is not proved but is true through reasoning.
3.what is the answer to this problem?

Answers
Domain is input so x axis So list all the x axis
Range is output so y axis and list all y axis
Example 3: Random variable X is distributed with the following pdf. sin(x), for 0 < xsa f(x)= 10, otherwise a. What is the value of the constant A? b. What is the corresponding CDF? c. What is E(x)? d. What is Var(x)?
Answers
The corresponding CDF is:F(x) = 1 - cos(x) for 0 < x < π/2F(x) = 1 for x ≥ π/2c. The expected value or mean of the given random variable X is 2. d. The variance of the given random variable X is π²/4 + 2π - 6.
The value of the constant A can be obtained by using the normalization condition that the integral of the PDF function over the entire possible range of X must be equal to 1. So, we can write the following integral to solve for
A:(∫f(x) dx) from 0 to π/2=∫A sin(x) dx= A [-cos(x)] evaluated at π/2 and 0= -A(cos(π/2) - cos(0))= A (1 - 0) =1. Therefore, the value of the constant A is 1. b. The CDF of the given random variable X is given as follows:
F(x)=∫f(x)dx from 0 to x, for 0 < x < π/2=∫sin(x) dx from 0 to x= [-cos(x)] evaluated at x and 0= -cos(x) - (-cos(0))= 1 - cos(x) for 0 < x < π/2=1 for x ≥ π/2. So, the corresponding CDF is as follows:
F(x) = 1 - cos(x) for 0 < x < π/2F(x) = 1 for x ≥ π/2c. The expected value or mean of the given random variable X can be obtained using the following formula:
E(X) = ∫xf(x)dx from 0 to π/2=∫x sin(x) dx from 0 to π/2= [-x cos(x)] evaluated at π/2 and 0 - ∫-cos(x) dx from 0 to π/2= -0 + cos(0) - ([-cos(x)] evaluated at π/2 and 0)= 0 + 1 - (-1)= 2. So, the expected value of the given random variable X is 2.
d. The variance of the given random variable X can be obtained using the following formula:
Var(X) = E(X²) - [E(X)]²=∫x² f(x)dx from 0 to π/2 - [E(X)]²=∫x² sin(x)dx from 0 to π/2 - (2)²= [-x² cos(x)] evaluated at π/2 and 0 + ∫2x cos(x)dx from 0 to π/2 - 4= -0 + π²/4 - 4 + (2 sin(x) + 2x cos(x)) evaluated at π/2 and 0= π²/4 - 2 - 4 + 2 + 2π= π²/4 + 2π - 6. So, the variance of the given random variable X is π²/4 + 2π - 6
Hence, the answer is: a. The value of the constant A is 1.b. The corresponding CDF is : F(x) = 1 - cos(x) for 0 < x < π/2F(x) = 1 for x ≥ π/2c. The expected value or mean of the given random variable X is 2. d. The variance of the given random variable X is π²/4 + 2π - 6
To know more about corresponding visit:
brainly.com/question/31493107
#SPJ11
This graph represents the first hypothetical described in the video. Imagine someone invests $10,000 with 7% returns compounding each year for 30 years.
Answers
Using the formula of compound interest, the amount compounded annually for 30 years at a rate of 7% is $76,122.55
Compound InterestThe compound interest is the interest-based on the initial principal amount and the interest collected over the period of time. The compound interest formula is given below:
A = P(1 + r/n)^nt
Compound InterestP = principalr = rate n = number of times compoundedt = timeSubstituting the values into the equation above;
A = 10000(1 + 0.07/1)^1 * 30
A = $76,122.55
The amount at the end of 30 years is equal to $76,122.55
Learn more on compound interest here;
https://brainly.com/question/24924853
#SPJ1
Which factors affect the resistance of a material? Select three options.
Olength
current
thickness
O temperature
voltage
Answers
Answer:
They are length, thickness and temperature
Tommy has 7 apples his mom takes away 3 how much he has now?
Answers
Answer:
4 apples
yeaaaaaaaaaaaaaaaaaaahhhhhh
Answer:
ele tem 4 maçãs
Step-by-step explanation:
determine the volume of the solid with a circular base of radius whose cross sections are squares that are perpendicular to the base.
Answers
\(V = πr^2h = πr^2 * (4/π) = 4r^2.\) The volume of the cylinder with a radius r and a cross-section perpendicular squares. To determine the volume of a solid with a circular base and cross sections that are perpendicular squares, we need to use the formula for the volume of a cylindrical shell.
Radius can r according to the formula that is given the volume is already mentioned.
\(V = πr^2hh\) is the height of the cylinder. Squares are the cross section of cylinders, side length can be equal to 2r. So, the area of each cross-section is \((2r)^2 = 4r^2.\)
The h in consideration of the area of cross-section h = Area of the cross section \(/ πr^2h = (4r^2) / πr^2 = 4/π\)The volume of the shell of the cylinder is \(V = πr^2h = πr^2 * (4/π) = 4r^2\)The volume of the cylinder with a radius r and a cross-section perpendicular squares.
To know more about the volume
brainly.com/question/1578538
#SPJ4
The formula E=220+0.07S is a formula for the earnings, E, of a salesman who receives $220 per week plus 7% commission on all weekly sales, S. Find the earnings of a salesman who had weekly sales of $1250.
Answers
The earnings of the salesman with weekly sales of $1250 would be $307.5. The formula E = 220 + 0.07S represents the earnings, E, of a salesman who receives a fixed weekly amount of $220 plus a 7% commission on all weekly sales, S. To find the earnings of a salesman who had weekly sales of $1250, we substitute the value of S = $1250 into the formula.
Plugging in S = $1250, we have:
E = 220 + 0.07 * 1250
Simplifying the expression:
E = 220 + 87.5
E = 307.5
Therefore, the earnings of the salesman with weekly sales of $1250 would be $307.5.
This means that the salesman would receive a base salary of $220 per week, and in addition to that, they would earn a commission of 7% on their weekly sales of $1250, which amounts to $87.5. When we add the base salary and the commission together, the total earnings for that week amount to $307.5.
Learn more about amount here:
https://brainly.com/question/31102401
#SPJ11
In a right triangle ABC, a circle with a side AB as diameter is drawn to intersect the hypotenuse AC in P. Prove that the tangent to the circle at P bisect the side BC
Answers
In a right triangle ABC, a circle with a side AB as diameter is drawn to intersect the hypotenuse AC in P. Proved that the tangent to the circle at P bisects the side BC.
First, note that since AB is a diameter of the circle, angle APB is a right angle. Therefore, we have
angle APB = 90 degrees
Also, since AP and PB are radii of the circle, they have equal length:
AP = PB
Now, let Q be the point where the tangent to the circle at P intersects BC. We want to show that Q is the midpoint of BC, i.e., we want to show that
BQ = QC
To do this, we will use the fact that tangents to a circle from a point outside the circle are equal in length. This is known as the tangent-chord theorem. Specifically, we can use this theorem to find the lengths of BQ and QC in terms of AP and PB.
Consider the tangent to the circle at P. Let R be the point where this tangent intersects AB. Then, by the tangent-chord theorem, we have
BR = BP
Similarly, let S be the point where the tangent to the circle at P intersects AC. Then
AS = AP
Now, note that triangles APR and BPQ are similar, since they share angle P and have a right angle at P. Therefore
BP / BQ = AP / PR
We can rewrite this as
BQ = BP × PR / AP
Similarly, triangles BPQ and CPS are similar, since they share angle P and have a right angle at P. Therefore
CP / CQ = BP / PQ
We can rewrite this as:
CQ = BP × PQ / CP
Now, we want to show that BQ = QC. To do this, we will substitute the expressions we just found for BQ and CQ in terms of AP and PB:
BQ = BP × PR / AP
CQ = BP × PQ / CP
We can rewrite these as
BQ = BP × (AP - AR) / AP
CQ = BP × (AS - AP) / CP
Now, using the fact that AP = AS (since AP is a radius of the circle), we can simplify these expressions
BQ = BP × (AS - AR) / AS
CQ = BP × (AS - AP) / CP
Since AS - AR = AP, we can simplify further:
BQ = BP × AP / AS
CQ = BP × CP / AS
Now, using the fact that AP = PB and AS = PC (since AP and PB are radii of the circle, and AS and PC are radii of the circle), we can simplify even further
BQ = PB × PB / PC
CQ = PB × PC / PB
Simplifying these expressions gives
BQ = PB
CQ = PC
Therefore, BQ = QC, as desired. This shows that the tangent to the circle at P bisects BC.
Learn more about tangent here
brainly.com/question/29030115
#SPJ4
Consider a tank used in certain hydrodynamic experiments. After one experiment, the tank contains 200 liters of a dye solution with a concentration of 1 g/liter. To prepare for the next experiment, the tank is to be rinsed with fresh water flowing in at a rate of 2 liters/min, the well-stirred solution flowing out at the same rate. Find the time that will elapse before the concentration of dye in the tank reaches 1% of its original value.
Answers
The time that will elapse before the concentration of dye in the tank reaches 1% of its original value is 460.52minutes by using differential equation.
Let t denote the time in minutes, V = V (t) denote the amount of liquid in liters, and m = m(t) denote the amount of dye in grams. The tank initially has a capacity of 200 L and a concentration of 1\(\frac{g}{L}\), or mass of dye per unit volume.
P(t)=quantity of dye in tank after t min
P(0)=200
by using differential equation
\(\frac{dQ(t)}{dt}\)= rate in and rate out
\(\frac{dQ(t)}{dt}\)=-2\(\times \frac{Q(t)}{200} =- \frac{Q(t)}{100}\)
Q(t)=c×\(e^{\frac{-t}{100}}\)
200=Q(0)=c×\(e^0\)\(\rightarrow c=200\)
Q(t)=200×\(e^{\frac{-t}{100}}\)
1% of 200 is 2 grams
2=200×\(e^{\frac{-t}{100}}\)
\(e^{\frac{t}{100}}\)=100
t=100ln(100)
t=460.52minutes
Learn more about differential equation
brainly.com/question/14620493
#SPJ4
The area of a square plot is 100 sq m. The cost of fencing around the plot at rupees.15 per meter pls pls pls pls pls answer it step by step it would be a great pleasure!!
Answers
Answer: cost of fencing = 15 x 40 = 600 rupees
Step-by-step explanation:
To find the cost of fencing around the plot, we have to calculate the PERIMETER (p).
Area = 100 sq. m.
Side = √100 = 10 m
Perimeter = 4s = 4 x 10 = 40 m
Find the greatest common factor (GCF) for each number set. 56,63
1. 1
2. 6
3. 7
Answers
What is the greatest common
factor of the following three
numbers?
12, 18,32
Answers
hope this helps
Answer:
2
Step-by-step explanation:
12:1,2,3,4,6,12
18:1,2,3,6,9,18
32:1,2,4,8,16,32
h.c.f = 2
HELP ASAP!!
What is Y when x = 40
A) about 92
B) about 98
C) about 155
D) about 170

Answers
Answer:
y = 155
Step-by-step explanation:
x is the distance from y-axis. Mark the line x = 40 and see the y-value where the (blue) line meets the given line.
In the graph, 1 cm = 25 unit. Each line is 2.5 units

Answer:
C) about 155
Step-by-step explanation:
To figure out the y-value of the line when x = 40, first look at the x-axis (horizontal axis) at the bottom of the graph, then find where it is labeled 40. From there, look up until you find the orange line. Finally, look left until you see the approximate value on the y-axis (vertical position) of the orange line at that point. In this case, we can see that it is about 155.

If the board length of an average log is 8.25 and the price per board foot is 7.95. What is the value of the timber if there are 100 logs?
Answers
Answer:
6558.75
Step-by-step explanation:
total value of 100 logs = total value of an average log x 100 total value of an average log = length of an average log x price per board foot
8.25 x 7.95 = 65.5875
65.5875 x 100 = 6558.75
what expression can represent 4 more than the product of 6 and 2 1/2
Answers
Answer:
6 x 2 1/2 + 4 ??? I hope this is correct :)
Step-by-step explanation:
If its not.. I'm so sorry:(
Have a nice day! <3
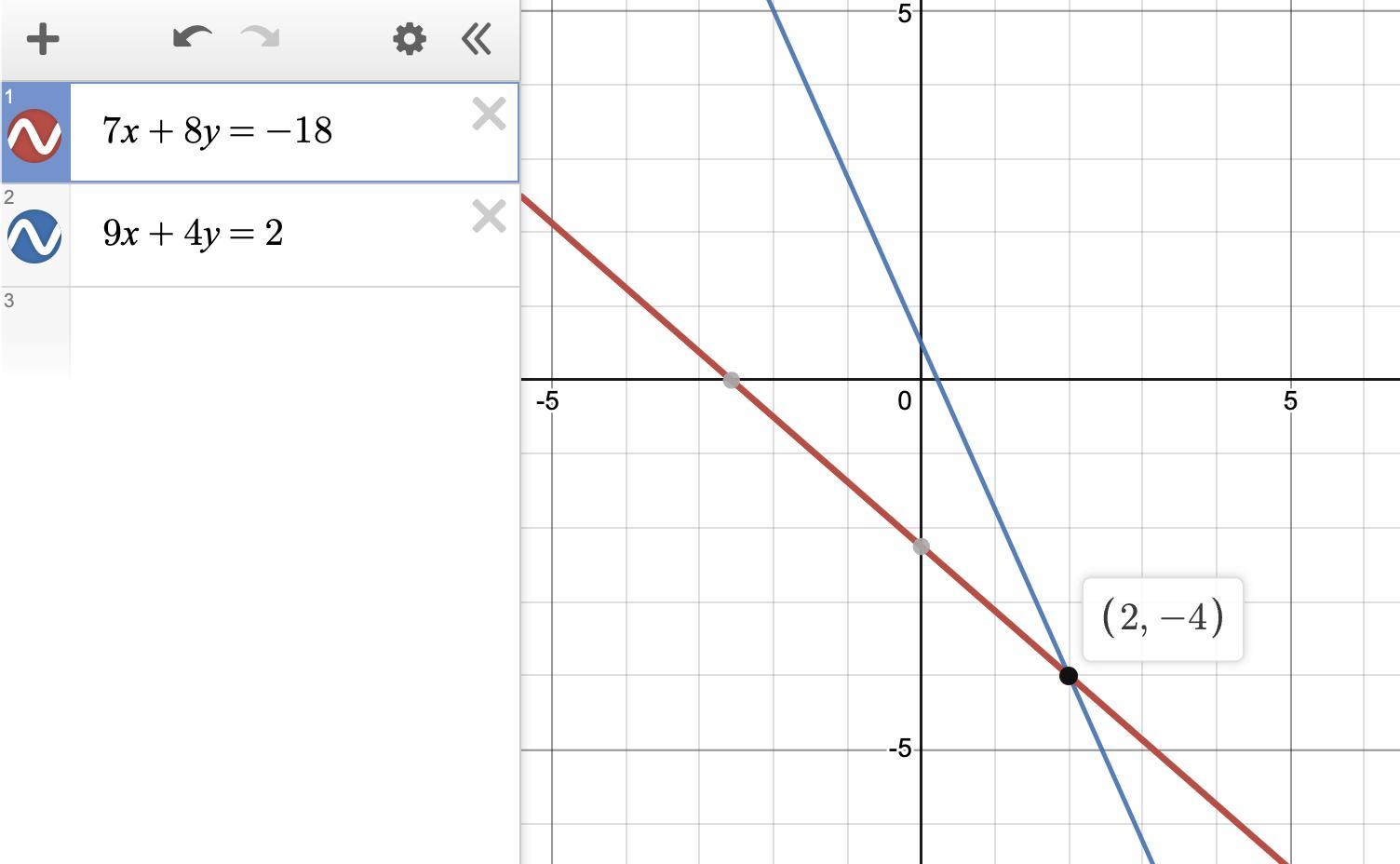
7x + 8y = -18 9x + 4y = 2
Answers
Answer:
(x, y) = (2, -4)
Step-by-step explanation:
No question is posed, and no solution method is specified. We presume you're interested in the values of x and y that make both equations true.
SolutionA quick and easy way to find the solution of two linear equations is to type them into a graphing calculator. The result is shown in the attachment.
The solution is the point that satisfies both equations, their point of intersection. The solution is (x, y) = (2, -4).
__
Additional comment
We note that the y-coefficients are related by a factor of 2, and the other coefficients of the second equation are larger than those of the first equation. This suggests using "elimination" or "linear combination" to solve the equations by eliminating the y-variable.
Subtracting the first equation from twice the second gives ...
2(9x +4y) -(7x +8y) = 2(2) -(-18)
11x = 22 . . . . . . . simplify
x = 2 . . . . . . . . divide by 11
Substituting for x in the second equation gives ...
9(2) +4y = 2
4y = -16 . . . . . . . . subtract 18
y = -4 . . . . . . . divide by 4
The solution is (x, y) = (2, -4).
Gianelli earns $4.50 per hour. If she works 8 hours per day and 5 days a week, how much will she earn in one week?
$32.40
$36.00
$162.00
$180.00
Answers
PLZ HELP THIS DUE TODAY
20 points for correct answer
Answers
Answer: solid geometry
Solid geometry has to do with three-dimensional objects.
:)
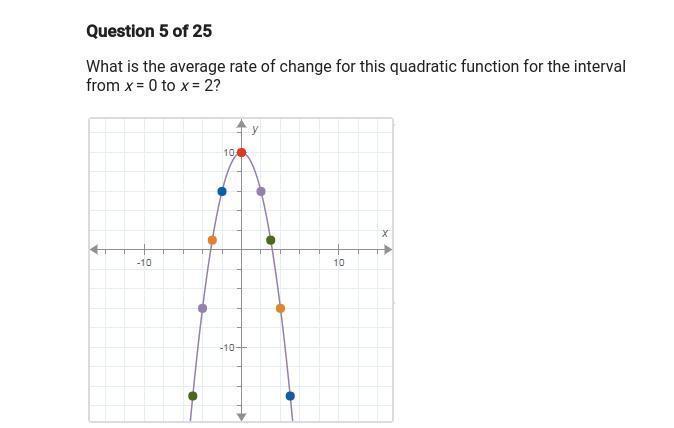
What is the average rate of change of the function from x = 0 to x = 2?.
Answers
The average rate of change of the function from x = 0 to x = 2 is -2
From the complete question (see attachment), we have the following ordered pair when x = 0 and x = 2
\((x,y) = \{(0,10)\ (2,6)\}\)
The average rate of change is calculated using:
\(\Delta x = \frac{y_2 -y_1}{x_2 -x_1}\)
So, we have:
\(\Delta x = \frac{6-10}{2-0}\)
Evaluate common terms
\(\Delta x = \frac{-4}{2}\)
Divide -4 by 2
\(\Delta x = -2\)
Hence, the average rate of change of the function from x = 0 to x = 2 is -2
Read more about rate of change at:
https://brainly.com/question/8728504
write the integral 3 1 dx as a limit of the riemann sum. you do not 1x need to evaluate this limit.
Answers
The integral of 3 from 1 to x can be expressed as the limit of a Riemann sum, where the sum of 3 times the width of each interval approaches the integral as the number of intervals becomes infinitely large.
To express the integral 3 1 dx as a limit of a Riemann sum, we divide the interval [1, x] into smaller subintervals. Let's denote the number of subintervals as n. The width of each subinterval is Δx = (x - 1) / n.
Now, we can approximate the integral using a Riemann sum:
∑(i=1 to n) 3Δx
This sum represents the sum of the areas of n rectangles, where the height of each rectangle is 3 and the width is Δx. The total width of all the rectangles is (x - 1), so the sum simplifies to:
3 * ∑(i=1 to n) Δx
As n approaches infinity, Δx approaches zero. Taking the limit as n approaches infinity, we get:
lim(n→∞) 3 * ∑(i=1 to n) Δx
This limit represents the Riemann sum approaching the value of the integral:
∫[1, x] 3 dx
Thus, the integral 3 1 dx can be expressed as the limit of the Riemann sum:
lim(n→∞) 3 * ∑(i=1 to n) Δx
Note that we didn't evaluate the limit or provide the exact value of the integral because the question only asked for the expression as a limit of a Riemann sum.
Learn more about integral here: brainly.com/question/31433890
#SPJ11
Evaluate the expression when, m=-2
m²-6m-5
(Thank you for your help!)
Answers
Answer:
11
Step-by-step explanation:
\(m=-2\\m^2-6m-5\\=(-2)^2-6(-2)-5\\=4-(-12)-5\\=4+12-5\\=16-5\\=11\)
What is the area of the shaded rectangle!!! I need help asap

Answers
A=(3)(1) = 3
3/2 = 1.5 square units
solve using a2 + b2 = c2
show the work please :)

Answers
Answer: 19.20937
Step-by-step explanation:
a2=15
b2=12
c2=?
a2+b2=c2
15(15)+12(12)= c2
225+ 144=c2
√369= √c2
≐19.20937 ft
3√41
Decrease R700 in the ratio 3:2.
Answers
Answer:
R466.66...
Step-by-step explanation:
To decrease A in the ratio x : y (where x < y), we have to perform the following
\(A*\frac{x}{y}\) (as a proper fraction)
R700 * 2/3 = R466.66...
A cable hanging from the top of a building is 15m long and has a mass of 40kg. A 10kg weight is attached to the end of the rope. How much work is required to pull 5m of the cable up to the top? Give your answer as an exact number (assume acceleration due to gravity is 9.8ms−2).
Answers
It would require 490 joules of work to pull 5m of the cable up to the top.
To solve this problem, we need to use the formula for work:
Work = force x distance x cos(theta)
where force is the tension in the cable, distance is the distance moved, and theta is the angle between the force and the distance.
First, let's find the tension in the cable. The weight of the cable itself is negligible compared to the weight of the weight, so we can assume that the tension is equal to the weight of the weight:
Tension = weight of weight = 10kg x 9.8m/s² = 98N
Next, let's find the angle between the force and the distance. Since we are pulling the cable straight up, the angle is 0 degrees, so cos(theta) = 1.
Now we can plug in the values and solve for work:
Work = 98N x 5m x 1
Work = 490J
You can learn more about the distance at: brainly.com/question/26711747
#SPJ11
the club has 20 members, 7 of whom are seniors. if you pick a committee of 3 from this club, what is the probability that all 3 are seniors?
Answers
Answer:
7/20
Step-by-step explanation:
ok so it has 30 members, 7 are seniors it's possible. if there is multiple choice just let me know if it is not on there.
at what point (x,y) is the function f(x)=6−7x closest to the point (−10,−4)? enter an exact answer.
Answers
The exact solution of this equation involves solving a quadratic equation, which may not result in a simple integer value for x.
To find the point (x, y) on the function f(x) = 6 - 7x that is closest to the point (-10, -4), we need to minimize the distance between the two points.
The distance between two points (x1, y1) and (x2, y2) is given by the formula:
d = sqrt((x2 - x1)^2 + (y2 - y1)^2)
In this case, we want to minimize the distance between the point (-10, -4) and any point on the function f(x) = 6 - 7x. So we can set up the distance equation:
d = sqrt((-10 - x)^2 + (-4 - (6 - 7x))^2)
To find the point (x, y) that minimizes the distance, we can find the value of x that minimizes the distance equation. Let's differentiate the distance equation with respect to x and set it equal to zero to find the critical point:
d' = 0
Differentiating and simplifying the equation, we get:
(-10 - x) + (-4 - (6 - 7x))(-7) = 0
Solving this equation will give us the value of x at the closest point. Plugging this x-value into the function f(x) = 6 - 7x will give us the corresponding y-value.
Know more about distance here:
https://brainly.com/question/13034462
#SPJ11
Adam wants to create an outdoor rectangular kennel. The length will be three feet more than twice the width. Write and use an equation to find the length and width of the kennel if Adam has 54 feet of fencing. Write and solve an equation to solve this problem.
Answers
Step-by-step explanation:
l = 3 + 2w
P= 2w t 2l
= 2w+2(3+2w)
=2w+6+4w
=6w+6 = 54
6w=48
w=8
divide 6 both side
l=3+2(8)=3+16=19
answer
width 8feet and length 19 feet
Which describes the cross section of a square prism that passes through vertices A, B, and C?
Answers
The cross-section from any side in a square prism is always square.
What is cross-section?A cross-section is the non-empty intersection of a solid body in three-dimensional space with a plane, or the analog in higher-dimensional spaces. Cutting an object into slices creates many parallel cross-sections.
Cross-section of a square prism :-
The cross-section of a square prism is a square. Since a square prism has its faces shaped in square and all the edges of the square prism are equal in length.
Therefore, when we cut the cube by a plane, we get a square shape.
Hence, the cross-section from any side in a square prism is always square.
Learn more about cross-sections, click;
https://brainly.com/question/15541891
#SPJ9