ABC is an isosceles right triangle in which has a slope of -1 and mABC = 90°. ABC is dilated by a scale factor of 1. 8 with the origin as the center of dilation, resulting in the image A'B'C'. What is the slope of ?.

The altitude of the aircraft, to the nearest tenth of a kilometer, is approximately 4.1 km. This value is determined by using trigonometric calculations based on the given angles of elevation observed from two different points.

Let's consider the observer at one of the observation decks. From this observer's point of view, the angle of elevation to the aircraft is 70°. Similarly, the other observer, located 5.0 km away, sees the aircraft at an angle of elevation of 55°. We can use trigonometry to calculate the altitude of the aircraft.

To begin, we can label the distance between the observer's positions as 'd' (5.0 km) and the altitude of the aircraft as 'h'. Using trigonometry, the tangent function can be applied to find the height in relation to the distance:

tan(70°) = h/d   and   tan(55°) = h/(d + 5.0)

Solving these equations simultaneously, we can find the value of 'h'. Rearranging the first equation, we have h = d * tan(70°). Substituting the given values, we get h ≈ 5.0 km * tan(70°). Using a calculator, this simplifies to h ≈ 4.1 km.

Therefore, the altitude of the aircraft, to the nearest tenth of a kilometer, is approximately 4.1 km.

learn more about angles of elevation here: brainly.com/question/12324763

#SPJ11

Step-by-step explanation:

16/7 is your solution....

hope it helps

...

Answer:

infinite solutions

4x+ 12 - 4 = 4x + 8

4x + 8 = 4x + 8

Answer:

+6-6=0

so we need -6 to add in +6 to get 0

Step-by-step explanation:

i hope this will help you

\(solution \\ let \: the \: number \: be \: x \\ x + 6 = 0 \\ or \: x = 0 - 6 \\ x = - 6\)

hope this helps...

Good luck on your assignment...

Answer:

Hiya There

___________________

Y=1/2x+3 I believe

___________________

“Hope is being able to see that there is light despite all of the darkness.”

– Desmond Tutu

By using the equation for the perimeter, we will see that the width is 11 inches and the length 8 inches.

The frame is a rectangle. Remember that for a rectangle of length L and width W, the perimeter is:

P = 2*(W + L)

In this case we know that the perimeter is 38 inches, and the length is 3 inches shorter than the width, then we can write two equations:

38in = 2*(W + L)

L = W - 3in

Replacing the second equation in the first one we get:

38in = 2*(W + W - 3in)

38in = 4*W - 6in

38in + 6in = 4*W

44in = 4*W

44in/4 = W

11in = W

The width is 11 inches, and the length is 11in - 3in = 8 in.

Learn more about perimeter:

https://brainly.com/question/24571594

#SPJ1

First, we want to note two things:

We can describe this with an inequality:  x ≥ -10
Be sure you use ≥ and not >, since -10 is included.

We can describe this with interval notation: [ -10, infty )
Be sure you use [ and not ( on -10, since -10 is included.

You can also use set-builder notation: { x | x ≥ -10 }

The probability is 0.01087 (rounded to five decimal places).

Let's first consider the possible positions the piece can be in after 8 moves. Since the piece can only move up or to the right, it can be in any position on the line that goes from the starting position (lower left corner) to the upper right corner of the grid. Since there are 8 moves, this line consists of 9 points. We can count the number of ways the piece can get to each of these points using combinations.

For example, to get to the point that is 4 inches up and 4 inches to the right of the starting position, the piece must move up 4 times and to the right 4 times, in any order. This is equivalent to choosing 4 moves out of the 8 total moves to be "up" moves, which can be done in C(8,4) = 70 ways. Similarly, the number of ways to get to each of the other 8 points on the line can be calculated using combinations.

Now we need to find the number of ways the piece can end up at a point that is exactly 4 inches away from the starting position. There are two such points on the line, which are 4 inches up and 4 inches to the right, and 4 inches to the right and 4 inches up, respectively. The total number of ways the piece can get to either of these points is C(8,4) + C(8,4) = 140.

Therefore, the probability that the center of the piece will be exactly 4 inches away from where it started after 8 moves is 140 divided by the total number of ways the piece can end up, which is C(8+8,8) = C(16,8) = 12,870.

The probability is therefore:

P = 140/12,870 = 0.01087 (rounded to five decimal places).

for such more question on probability

https://brainly.com/question/13604758

#SPJ11

Slope Formula:

\(\displaystyle m = \frac{y_2 - y_1}{x_2 - x_1}\)

Differentiation

Derivative Rule [Product Rule]:
\(\displaystyle \frac{d}{dx} [f(x)g(x)]=f'(x)g(x) + g'(x)f(x)\)

Let's identify what the problem initially gives us:

This means that they give us the derivative of each respective curve at x = 2, since the definition of a derivative is the slope of the tangent line.

We are also given that some function \(\displaystyle r(x)\) is equal to \(\displaystyle p(x)q(x)\), where the functions are multiplied by each other.

We are then asked to find \(\displaystyle r'(2)\), which is the derivative of the \(\displaystyle r(x)\) function at x = 2.

In order to find the derivative of \(\displaystyle r(x)\), we will need to use the Product Rule, which states how to find a derivative of 2 functions being multiplied by each other. Note the equation given under "General Formulas and Concepts":

\(\displaystyle \begin{aligned}r(x) & = p(x)q(x) \\r'(x) & = \boxed{ p'(x)q(x) + p(x)q'(x) }\\\end{aligned}\)

∴ the derivative of \(\displaystyle r(x)\) is equal to \(\displaystyle \boxed{ r'(x) = p'(x)q(x) + p(x)q'(x) }\)

To find the derivative evaluated at x = 2, we substitute in x = 2 into our derivative:

\(\displaystyle\begin{aligned}r'(x) & = p'(x)q(x) + p(x)q'(x) \\r'(2) & = p'(2)q(2) + p(2)q'(2) \\\end{aligned}\)

This is where the graphs and their tangent lines come into play.

To find \(\displaystyle q(2)\) and \(\displaystyle p(2)\), we simply refer to the \(\displaystyle y = q(x)\) and \(\displaystyle y = p(x)\) graphs, respectively:

\(\displaystyle \begin{aligned}\implies r'(2) & = p'(2)(-1) + 3q'(2) \\& = \boxed{ -p'(2) + 3q'(2) }\end{aligned}\)

We have now simplified our derivative equation \(\displaystyle r'(2)\) to be:

\(\displaystyle\begin{aligned}r'(x) & = p'(x)q(x) + p(x)q'(x) \\r'(2) & = p'(2)q(2) + p(2)q'(2) \\& = -p'(2) + 3q'(2) \\\end{aligned}\)

To find \(\displaystyle p'(2)\) and \(\displaystyle q'(2)\), we refer to the tangent lines of the graphs \(\displaystyle y = p(x)\) and \(\displaystyle y = q(x)\), respectively. We will have to find their slopes (by the definition of a derivative) using the Slope Formula:

\(\displaystyle\begin{aligned}\therefore r'(2) & = -p'(2) + 3q'(2) \\ r'(2) & = -2 + 3 \bigg( \frac{-1}{3} \bigg) \\& = -2 - 1 \\& = \boxed{ -3 }\end{aligned}\)

\(\displaystyle \therefore \boxed{ r'(2) = -3 }\)

___

Learn more about derivatives: https://brainly.com/question/30146641

Learn more about Calculus: https://brainly.com/question/30194936

___

Topic: Calculus

Unit: Derivatives

The probability to select $5 bill when the first selected bill is $10 is given by 1/2.

Probability is the possibility to occur of an event.

In mathematical terms, probability can be defined as,

\(\text{Probability}=\frac{\text{The number of favorable case}}{\text{The total number of case}}\)

Given that, the number of total $5 bills = 3

the number of $10 bills = 4

Total number = 3+4 = 7

If the first drawn bill is $10, then the number of $10 bills = 4-1 = 3

Total number of bills =7-1 = 6

So the probability to select $5 bill when the first selected bill is $10 = 3/6 = 1/2

Hence, the probability to select $5 bill when the first selected bill is $10 is given by 1/2.

To know more about Probability refer to:

https://brainly.com/question/24756209

#SPJ9

Answer:

5

Step-by-step explanation:

Answer:

5

Step-by-step explanation:

Answer: − 18 x= 72

Step-by-step explanation:

The point where the tangent plane to the surface is horizontal will be (1.0899, 1.6595).

To determine the partial derivatives of the function f(x, y) with respect to x and y:

\(fx = 2xy^3 - 4y - 1\\fy = 2x^3y - 4x\)

Now, we can find the gradient of f:

\(grad(f) = < fx, fy > = < 2xy^3 - 4y - 1, 2x^3y - 4x >\)

To determine the point where the tangent plane to the surface is horizontal, the critical points of f where grad(f) = 0:

\(2xy^3 - 4y - 1 = 0\\2x^3y - 4x = 0\)

From the second equation,

\(2x(x^2y - 2) = 0\)

Therefore, either x = 0 or x^2y - 2 = 0 Substituting this into the first equation, we get:

\(2x(2/x^6) - 4(2/x^2) - 1 = 0\\4/x^5 - 8/x - 1 = 0\)

Therefore, the point where the tangent plane to the surface is horizontal  x ≈ 1.0899 and y ≈ 1.6595.

Learn more about equations here;

https://brainly.com/question/25180086

#SPJ4

The given order of integration is in the form of triple integrals, where the integration is performed first over the z-coordinate, then over the y-coordinate, and finally over the x-coordinate.

To obtain an equivalent integral in the given order of integration, we can use the substitution method and change the order of integration.

First, we integrate with respect to z from 0 to √(4-x^2), then we integrate with respect to y from -√(4-x^2) to √(4-x^2), and finally, we integrate with respect to x from 2 to 0. This can be expressed as:

∫2 0 ∫-√(4-x^2) √(4-x^2) ∫0 f(x,y,z) dz dy dx

We can then change the order of integration to obtain an equivalent integral in the form ∫ba∫g(z)f(z)∫k(x,z)h(x,z)f(x,y,z)dydxdz by integrating w.r.t. x first, then w.r.t. y, and finallyw.r.t. z.

This gives us:

∫0 √4-y^2 ∫-√(4-x^2) √(4-x^2) ∫0 f(x,y,z) dz dx dy

Using the limits of integration for each variable, we can rewrite this as:

∫0 2 ∫-√(4-y^2) √(4-y^2) ∫0 f(x,y,z) dz dy dx

Therefore, the equivalent integral in the given order of integration is ∫0 2 ∫-√(4-y^2) √(4-y^2) ∫0 f(x,y,z) dz dy dx.

To know more about equivalent integral, visit:

https://brainly.com/question/31744185

#SPJ11

Answer:

a. Total field goal points scored in the first two quarters, in simplest linear expression form is: 3x - 4.

b. The total points scored in the game, in simplest linear expression form is: 6x - 1.

a. The goal points scored in the first two quarters are expressed in linear forms as: 2x - 6 and x + 2.

The total field goal points in the first two quarters = 2x - 6 + x + 2

Add like terms

3x - 4

b. The total points scored in the game = 2x - 6 + x + 2 + 2x + x - 6 + 9

Add like terms and simplify the expression

2x - 6 + x + 2 + 2x + x - 6 + 9

6x - 1

Step-by-step explanation:

The doctor used inductive reasoning because the doctor used various observations to come up with a final conclusion.

Since the Mean is of mean daily revenue of $5400

Also, the standard deviation is $54

For the sample mean

The mean and standard deviation will remain unchanged

Hence the answer is

Option A

The average of the last three numbers is 58 if the average of the five numbers in a list is 54. the average of the first two numbers is 48.

It is defined as the single number that represents the mean value for the given set of data or the closed value for each entry given in the set of data.

It is given that:

The average of the five numbers in a list is 54. and the average of the first two numbers is 48.

54 = sum of the five numbers/5

54x5 = sum of the five numbers

270 = sum of the five numbers

48 = sum of the two numbers/2

48x2 = sum of the two numbers

96 = sum of the two numbers

Sum of three numbers = 270 - 96

Sum of three numbers = 174

The average of the last three numbers = 174/3 = 58

Thus, the average of the last three numbers is 58 if the average of the five numbers in a list is 54. the average of the first two numbers is 48.

Learn more about the average here:

brainly.com/question/24057012

#SPJ4

Coach Burke's emphasis on proper hitting mechanics during Tuesday's practice at the ball field led to impressive results among the players. By focusing on elements such as stance, grip, and swing, the players were able to improve their overall hitting performance.

Their increased hitting distance can be attributed to several factors.

First, a balanced and comfortable stance allowed the players to transfer their weight effectively and generate more power in their swings. Secondly, a firm yet relaxed grip on the bat helped maintain proper bat control, ensuring that the players were able to hit the ball with maximum force. Additionally, an efficient and smooth swing, with a proper follow-through, allowed the players to make solid contact with the ball, thus increasing the hitting distance.

As a result of Coach Burke's guidance in refining these aspects of hitting mechanics, the players were able to hit the ball off the outfield fence and even over the fence during batting practice.

This improvement in hitting distance is a testament to the importance of mastering the fundamentals of baseball and the impact of quality coaching on player performance.

To learn more about factors click here

brainly.com/question/29128446

#SPJ11

The students were interested in the proportion of rental apartments in these suburbs that were leased as furnished apartments and whether this varied with the number of bedrooms in these apartments 500x + 900y + 1500z = 750,000

formal test, using a = 0.05,of whether the proportions of furnished apartments varies across number of bedrooms, that is, whether the furnishing status of an apartment independent of the number of bedrooms in the apartment You may use R to carry out these calculations, but please state the following information from this test: i. the table of expected frequencies ii. the observed value of the test statistic iii. the relevant degrees of freedom for the distribution of the test statistic iv

500x + 900y + 1500z = 750,000 - - - (1)

x + y + z = 1000 - - - - (11)

x = 200 + y + z - - - - (111)

x + 2y + 3z = 1550 - - - (1V)

I bedroom = x

2 bedroom = y

3 bedroom = z

All the condition s gjvbbs'

500x + 900y + 1500z = 750,000 - - - (1)

x + y + z = 1000 - - - - (11)

x = 200 + y + z - - - - (111)

x + 2y + 3z = 1550 - - - (1V)

learn more about of apartment here

https://brainly.com/question/22674586

#SPJ4

Answer:

The number of times a variable appears in a date set is called a constant.

Answer: 0.11

Step-by-step explanation:

Suppose y represents the cost, x represents the number of pictures, then y=kx {positive proportional function}

when x=50, y=5.5

5.5=50k

k=5.5/50

k=55/500

k=0.11

✧･ﾟ: *✧･ﾟ:*hello there!*:･ﾟ✧*:･ﾟ✧

✧here is your answer:

.・゜゜・d. 2s + 6・゜゜・．

♥⛧i hope this helps!!

✧༺♥༻∞lmk if you need help on anything else!!∞༺♥༻✧

❀-kay♬

Assuming that the national average score on a standardized test is 1010, and the standard deviation is 200, where scores are normally distributed, the probability, expressed as a percentage, that a test taker scores at least 1600 on the test can be calculated as follows:

First, we standardize the test score of 1600 using the formula below:

Z = (X - μ)/σ

where Z is the standard score or z-score,

X is the test score,

μ is the population mean,

and σ is the population standard deviation.

Substituting the given values, we have:

Z = (1600 - 1010)/200Z = 2.95

The probability of obtaining a test score of at least 1600 on the test is the area to the right of the standard score of 2.95 under the normal distribution curve using a z-table or a calculator.

Rounding off to two decimal places, we get:

P(Z > 2.95) = 0.0029 or 0.29%

Therefore, the probability, expressed as a percentage, that a test taker scores at least 1600 on the test is 0.29%.

To learn more about “probability” refer to the https://brainly.com/question/13604758

#SPJ11

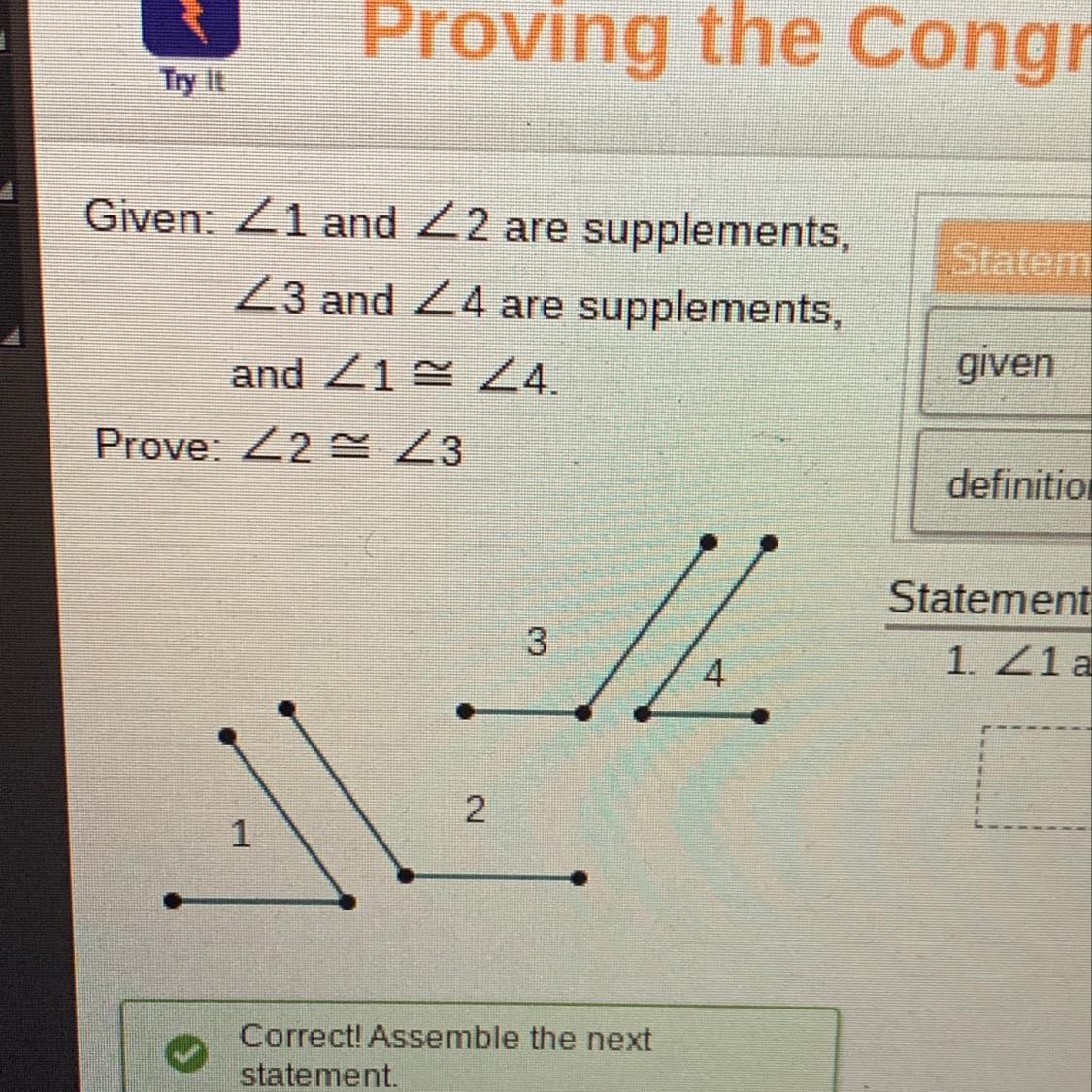
Answer:

see below

Step-by-step explanation:

<1 and <2 are supplements

<3 and <4 are supplements

<1 is congruent to <4

∠1 + ∠2 = 180     definition of supplementary angles

∠3 + ∠4 = 180    definition of supplementary angles

 ∠1 + ∠2 = ∠3 + ∠4    transitive property of equality

 ∠1 = ∠4                      given

 ∠1 + ∠2 = ∠3 + ∠1     substitution property of equality

∠2 = ∠3                     subtraction property of equality

∠2 ≅ ∠4                   definition of congruent angles

Answer:

$140,000

Step-by-step explanation:

Value of lottery = $1,500,000

Man's ratio = 41

Wife's ratio = 34

Total ratio = 41 + 34 = 75

Man's share = Man's ratio / Total ratio * Value of lottery

= 41/75 * $1,500,000

= 0.5466666666666 * $1,500,000

= $820,000

Wife's share = wife's ratio / total ratio * Value of lottery

= 34/75 * $1,500,000

= 0.4533333333333 * $1,500,000

= $680,000

Difference between the man's share and his wife's share

= Man's share - wife's share

= $820,000 - $680,000

= $140,000

Answer:

Step-by-step explanation:

The toy cars Anna must sell for her revenue to equal her expense is 4 toy cars. The result is obtained by using the concept of calculating algebra.

To calculate the algebra with one variable, sum up all the same variable and count the value.

Anna want to sell toy car at a craft fair. Each car is sold at a price of $ 12. The material for each car cost $ 3.50 and the table rental at the fair is 34 dollar for the day.

Find the toy cars must Anna sell for her revenue to equal her expense!

We have

Let's say

Revenue = Expense

a × $12 = (a × $3.5) + $34

12a = 3.5a + 34

12a - 3.5a = 34

8.5a = 34

a = 4 toy cars

Hence, Anna must sell 4 toy cars so that her revenue is equal to expense.

Learn more about algebra here:

brainly.com/question/24875240

#SPJ4

Answer:

14.49

Step-by-step explanation:

14 * 0.035 = 0.49

14 + 0.49 = 14.49