A rectangle that is 2 cm by 3 cm has been scaled by a factor of 5. What are the dimensions of the new rectangle? A.7 cm by 8 cm B.10 cm by 15 cm C.25 cm by 35 cm D.12 cm by 15 cm
Answers
Dimensions of new rectangle after getting scaled by factor of 5 are 10cm by 15cm. Option (B) is correct.
What is scale factor?
In two similar geometric figures the ratio of their corresponding side is scale factor let the old dimension be x and scale factor be a then new dimension will be a*x
If a>1 then their will be enlargement in the geometric figures
Given that rectangle that is 2 cm by 3 cm has been scaled by a factor of 5
It means scale factor be 5
New dimensions of given rectangle will be found by multiplying by 5
New length and breadth are 2*5=10
3*5=15
Learn more about scale factor at
https://brainly.com/question/9094355
#SPJ1
Related Questions
There is a bag filled with 5 blue and 6 red marbles.
Marble is taken at random from the bag, the colour is noted and then it is replaced.
Another marble is taken at random.
What is the probability of getting 2 reds?
thanks,
Answers
Answer:
\((\frac{6}{11} )*(\frac{6}{11} )\) = 36/121 =.297
Step-by-step explanation:
Answer:
36/121
Step-by-step explanation:
We have 5+6 = 11 marbles
P(red) = number of red/ total = 6/11
We replace the marble so we still have 11 marbles
P(red) = number of red/ total = 6/11
P(red, red) = 6/11*6/11 = 36/121
Parallelogram JKLM has vertices J(2, 1), K(7, 1), L(6,-3), and M(1, -3). What are the coordinates of the image of K if the parallelogram is rotated
270 counterclockwise about (-2,- 1)?
Answers
If the parallelogram is rotated 270° about the origin. Then the coordinate of the image will be (1,-2), (1,-7), (-3, -6), and (-3, -1).
What is coordinate geometry?Coordinate geometry is the study of geometry using the points in space. Using this, it is possible to find the distance between the points, the dividing line is m:n ratio, finding the mid-point of the line, etc.
Parallelogram JKLM has vertices J(2, 1), K(7, 1), L(6, −3), and M(1, −3).
If the parallelogram is rotated 270° about the origin. Then the coordinate of the image will be
J(2, 1) → (1, -2)
K(7, 1) → (1, -7)
L(6, −3) → (-3, -6)
M(1, −3) → (-3, -1).
To learn more about Coordinate geometry refer to:
brainly.com/question/1601567
#SPJ1
What are the solutions of the equation x4 + 6x2 + 5 = 0? use u substitution to solve. X = i and x = i i and x = i and x = and x = -.
Answers
The given equation's solution is x = 5i or x = i.
An equation has been provided.
x⁴+6x²+5 = 0
We to settle it utilizing replacement.
If u = x2, then u2 = x4 In the above equation, we find that u2+6u+5 = 0. Now, use the factorization method.
Divide the middle term of the previous equation as follows: u2+5u+u+5 = 0; u(u+5)+1(u+5) = 0; u(u+5)(u+1) = 0 Using the zero-product property, we can determine that u+5 or u+1 equals 0; u = -5 or u = -1; x2 equals -5 or x2 equals -1; taking the square root of both sides of.
To learn more about factorization method here
https://brainly.com/question/17325738
#SPJ4
identifying the coefficients and constant of a quadratic function consider the quadratic function f(x) = x2 – 5x 6. what are the values of the coefficients and constant in the function? a = b = c =
Answers
For the quadratic function f(x) = x^2 - 5x + 6, the values of the coefficients and constant are:
a = 1
b = -5
c = 6.
To identify the coefficients and constant in the quadratic function f(x) = x^2 - 5x + 6, let's examine the standard form of a quadratic equation:
f(x) = ax^2 + bx + c
Comparing this with the given quadratic function, we can determine the values of the coefficients and constant:
a = 1 (coefficient of x^2 term)
b = -5 (coefficient of x term)
c = 6 (constant term)
Therefore, for the quadratic function f(x) = x^2 - 5x + 6, the values of the coefficients and constant are:
a = 1
b = -5
c = 6.
Visit to know more about Constant:-
brainly.com/question/27983400
#SPJ11
The sales of Horizon, a cell phone sales and service provider, were $127,693,100 last year. What is the value of the 6th digit in this number?
Answers
Answer:
600000
Step-by-step explanation:
Cuz it is in the 100000 spot
Answer:
600000
Step-by-step explanation:
Based on the place value system, the digits are ordered from the right to left. So the 6th digit is 6 located in the hundreds of thousands column. The value of the 6th digit is obtained by multiplying the digit by the value of it's place value column
i.e 6 * 100,000 = 600, 000
Ans: 600,000
The number of gold medals won by ten countries during the 1996 Olympics are given below. Use the data to make a stem and leaf plot. (9,16,9,15,20,13,7,26,9,44)
Answers
Answer:
0| 7, 9,9,9
1| 3,5,6
2| 0,6
3|
4| 4
Notation: For this case the first number represent the first digit and the second represent the second digit.
Step-by-step explanation:
For this case we have the following dataset given:
9,16,9,15,20,13,7,26,9,44
The first step is order the data on increasing way and we got:
7,9,9,9, 13,15, 16,20,26,44
And we can create the stem plot like this:
0| 7, 9,9,9
1| 3,5,6
2| 0,6
3|
4| 4
Notation: For this case the first number represent the first digit and the second represent the second digit
13. Fill in this diagram so that each of the rows, columns and
diagonals adds to 18.
What is the sum of all the corner numbers?
(A) 20
(B) 22
(C) 23
(D) 24
(E) 25
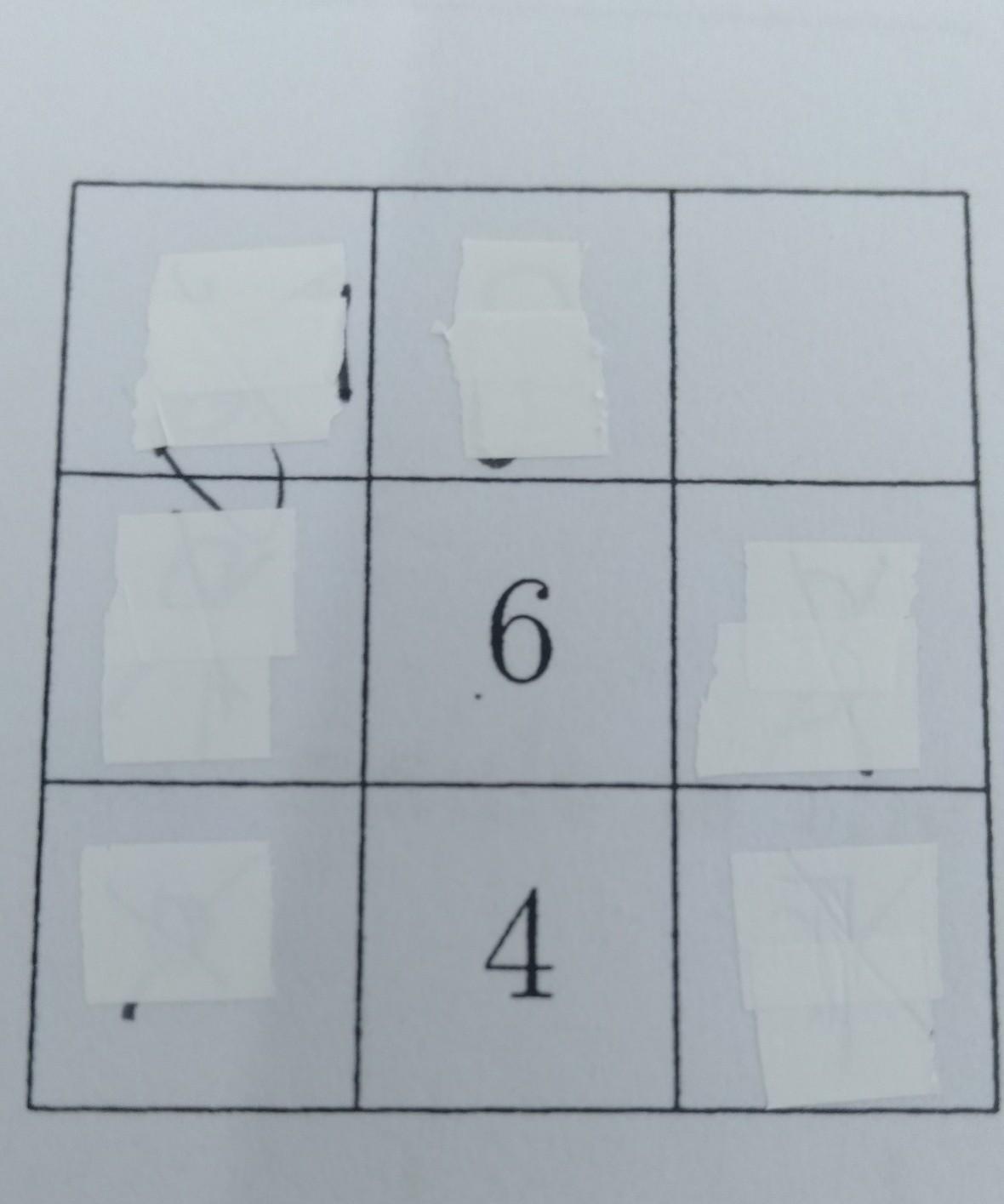
Answers
Answer:
D. 24
Step-by-step explanation:
Let's name the diagram
Row 1: a1, a2, a3
Row 2: b1, b2, b3
Row 3: c1, c2, c3
From the diagram,
b2 and c2 have been given
All rows, columns and diagonal must sum up to 18
If b2=6 and c2=4
a2=18-(6+4)
=18-10
=8
a2=8
Assume a1=4
Diagonals a1+b3+c3=18
4+6+c3=18
10+c3=18
c3=18-10
=8
Assume a3=6
Diagonals a3+b2+c1=18
6+6+c1=18
12+c1=18
c1=18-12
=6
So b1=18-(6+4)
=18-10
=8
b1=8
b3=18-(6+8)
=18-14
=4
b3=4
Input all the numbers into the boxes
We have,
4 8 6
8 6 4
6 4 8
Corner numbers are a1,a3,c1,c3
=4,6,6,8
Sum of all the corner numbers=4+6+6+8
=24
D. 24
using only the digits $7$, $8$ and $9$, how many positive seven-digit integers can be made that are palindromes?
Answers
Using the digits 7,8 and 9, the positive seven-digit integers can be made that are palindromes are 729.
When constructing a seven-digit palindrome out of the digits 7, 8, and 9, the first three digits must be the same as the last three digits in reverse order.
This means that each of the first three digits can be either a 7, 8, or 9. Therefore, the total number of combinations for the first three digits is 3 x 3 x 3 = 27.
Since the last three digits must match the first three, the total number of possible combinations of integers is 27 x 27 = 729.
Thus, the total number of positive seven-digit palindromes that can be created using the digits 7, 8 and 9 is 729.
To learn more about palindrome, click here:
https://brainly.com/question/24304125
#SPJ4
The diagram shows an open rectangular box ABCDEFGH.
A straight stick AGM rests against A and G and extends outside the box to M.
a. Calculate the angle between the stick and the base of the box.
b. AM= 30 cm.
Show that GM= 4.8 cm, correct
to 1 decimal place.

Answers
The angle between the stick and the base of the box is 77. 9 degrees
How to determine the angleTo determine the angle between the stick and the base, we have to know the trigonometric identities.
These identities are;
sinecosinecotangenttangentsecantcosecantFrom the information given, we have;
sin A = FB/AB
Given that;
GB = 14.5cm
AB = 18. 6cm
substitute for the length of the sides, we have;
sin A = 14.5/18. 6
Divide the values, we have;
sin A = 0. 7796
Find the inverse sine
A = 77. 9 degrees
Learn more about trigonometric identities at: https://brainly.com/question/7331447
#SPJ1
Solve equation show all steps what 2x-3x+5=18
Answers
●✴︎✴︎✴︎✴︎✴︎✴︎✴︎✴︎❀✴︎✴︎✴︎✴︎✴︎✴︎✴︎✴︎✴︎●
Hi my lil bunny!
❧⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯☙
Let's solve your equation step-by-step.
\(2x-3x+5=18\)
Step 1: Simplify both sides of the equation.
\(2x-3x+5=18\\2x + -3x + 5 = 18\)
\(( 2x + -3x ) + ( 5) = 18\) (Combine Like Terms)
\(-x + 5 = 18\\-x + 5 = 18\)
Step 2: Subtract 5 from both sides.
\(-x + 5 - 5 = 18 - 5 \\-x = 13\)
Step 3: Divide both sides by -1.
\(\frac{-x}{-1} = \frac{13}{-1} \\x = -13\)
Answer : \(\boxed {x = -13}\)
❧⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯☙
●✴︎✴︎✴︎✴︎✴︎✴︎✴︎✴︎❀✴︎✴︎✴︎✴︎✴︎✴︎✴︎✴︎✴︎●
Have a great day/night!
❀*May*❀
Answer:
\( \boxed{ \bold{ \mathsf{ \purple{x = - 13}}}}\)Step-by-step explanation:
\( \mathsf{2x - 3x + 5 = 18}\)
Collect like terms
\( \mathsf{ - x + 5 = 18}\)
Move constant to R.H.S and change it's sign
\( \mathsf{ - x = 18 - 5} \)
Calculate the difference
\( - x = 13\)
Change the signs on both sides of the equation
\( \mathsf{x = - 13}\)
---------------------------------------------------------------
\( \blue{ \mathsf{verification}}\)
\( \mathsf{LHS \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: RHS}\)
\( \mathsf{2x - 3x + 5 \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: 18}\)
\( \mathsf{ = 2 \times ( - 13) - 3 \times ( - 13) + 5}\)
\( \mathsf{ - 26 + 39 + 5}\)
\( \mathsf{ = 13 + 5}\)
\( = 18\)
Thus, LHS = RHS
hope I helped!
Best regards!
Suppose the difference between actual and predicted weekly sales of a company follows a uniform distribution between $2800 and $2800. Determine the following: a. The probability that the actual sale is under predicted by at least $1200? b. The probability that the actual sale is within $1300 of the predicted sale?
Answers
The probability distribution for the difference between actual and predicted weekly sales of the company is a uniform distribution between $2800 and $2800. Actualsale of under predicted is 4/7 and with in predicted sale is 13/14
(a) To find the probability that the actual sale is under predicted by at least $1200, we need to determine the area under the PDF to the left of $1200. Since the PDF is constant within the range, the probability is equal to the ratio of the difference between $1200 and $2800 to the total range of $2800. Therefore, the probability is (2800 - 1200) / 2800 = 1600 / 2800 = 4/7, or approximately 0.5714.
(b) To find the probability that the actual sale is within $1300 of the predicted sale, we need to determine the area under the PDF between $-1300 and $1300. Again, since the PDF is constant within the range, the probability is equal to the ratio of the difference between $1300 and $-1300 to the total range of $2800. Therefore, the probability is (1300 - (-1300)) / 2800 = 2600 / 2800 = 13/14, or approximately 0.9286.
In summary, the probability that the actual sale is under predicted by at least $1200 is 4/7, and the probability that the actual sale is within $1300 of the predicted sale is 13/14.
learn more about uniform distribution here
https://brainly.com/question/30639872
#SPJ11
Five years from now, a father's age will be tree times his son's age, and 5 years ago, he was seven times as old as his son was. What are their present age?
Answers
Answer:
The answer is "10 and 40".
Step-by-step explanation:
\(\to f + 5 = 3(s + 5) = 3s + 15\\\\\to f - 5 = 7(s - 5) = 7s - 35\\\\\)
Subtracting the equations to get
\(\to 10 = -4s + 50\\\\\to -40 = -4s\\\\\to s = \frac{40}{4} \\\\\to s=10\\\\\to f = 40\\\\\)
So the Son age is 10, and the father's age is 40.
PLEASE HELP ME ASAP FOR BRAINLIEST

Answers
Answer:
First one: true Second one: true
Step-by-step explanation:
First Question: the lines will be parellel even though the shape grows or gets smaller
Second Question: the angle will stay the same even if it grows into a larger or smaller shape.
If m= 2, n=3, and p= -1, then find the value of : 2mn4 – 15m2n + p
In Full Details!! As Soon As Possible
Answers
Answer:
-131
Step-by-step explanation:
2×2×3×4-15×2×2×3+-1
48-179
=-131
Because 2x2x3x4=48
And -15x2x2x3=-180.
48-180+(-1)=-133
19a + 44 - 19a
Need help with this was not paying attention in class
Answers
19a + 44 - 19a
Group like terms.
\(19a - 19a + 44\)
Add similar elements.
\(19a - 19a = 0\)
\(=44\)
Answer:
44
Step-by-step explanation:
Hahaha, fair enough.
This one may look more difficult than it is. In algebra, there are variables and there are constants.
A constant is a number that is constantly the same, in the example you posted, 44 is the constant.
A variable is like a place holder, it indicates that there is a number that will be substituted in, we just don't know what that number is yet. In your example, the variable is represented by the letter "a."
If youre still a little unsure what a variable is, think of it like this:
Every morning, you like to have one, single cup of coffee, but some days you feel like putting 1 spoon of sugar in, some mornings you want no sugar, and some mornings you really want something sweet and so you have 3 spoons of sugar.
In algebra, your morning cup of coffee is represented 1 + s. 1 is the number of cups of coffee you have and "s" represents how much sugar you put in it. "s" can equal 1, 3, or even 0 spoons of sugar. "s" will represent the number of spoons of sugar consistantly, BUT, keep in mind that while the value of a variable is the same within that one term or equation it can represent a different value in another term or equation.
1 + s on Monday could equal 4 because you really want some sugar at the beginning of your week so you put 3 sugars in. 1 + 3 = 4. But on Thursday, you don't want any sugar, so 1 + 0 = 1. Monday and Thursday are different terms/equations.
SO, because a variable always has the same value within a term/equation, in your example 19a + 44 - 19a, "a" will always have the same value. if a = 1 then your example is 19(1) + 44 - 19(1). If the value of "a" is 1,000,000, then your example looks like 19(1,000,000) + 44 - 19(1,000,000).
We can rewrite your question a little to make it clearer. 19a - 19a + 44, we just swapped the positions of 44 and -19a. So you can see, that no matter what value "a" represents, they will cancel each other out. leaving you with 44 as your answer.
-21 < a -16 please help me
Answers
Answer:
a > -5
Step-by-step explanation:
Step 1: Flip the inequality.
\(-21 < a - 16\) \(a - 16 > -21\)Step 2: Add 16 to both sides.
\(a - 16 + 16 > -21 + 16\) \(a > -5\)Therefore, a > -5.
Have a lovely rest of your day/night, and good luck with your assignments! ♡
Answer:
a > -5
Step-by-step explanation:
-21-(a-16)<0
Pull out like factors :
-5 - a = -1 • (a + 5)
Multiply both sides by (-1)
Flip the inequality sign since you are multiplying by a negative number
a+5 > 0
Subtract 5 from both sides
a > -5
PLEASE ASAP ILL GIVE BRAINLIEST.

Answers
Look at the equation below f(x)= x³ + x² - 10x + 8 Find the real roots using the method a. bisection. b. Newton-Raphson c. Secant With stop criteria is relative error = 0.0001%. You are free to make a preliminary estimate. Show the results of each iteration to the end.
Answers
a. Bisection Method: To use the bisection method to find the real roots of the equation f(x) = x³ + x² - 10x + 8, we need to find an interval [a, b] such that f(a) and f(b) have opposite signs.
Let's make a preliminary estimate and choose the interval [1, 2] based on observing the sign changes in the equation.
Iteration 1: a = 1, b = 2
c = (a + b) / 2
= (1 + 2) / 2 is 1.5
f(c) = (1.5)³ + (1.5)² - 10(1.5) + 8 ≈ -1.375
ince f(c) has a negative value, the root lies in the interval [1.5, 2].
Iteration 2:
a = 1.5, b = 2
c = (a + b) / 2
= (1.5 + 2) / 2 is 1.75
f(c) = (1.75)³ + (1.75)² - 10(1.75) + 8 ≈ 0.9844
Since f(c) has a positive value, the root lies in the interval [1.5, 1.75].
Iteration 3: a = 1.5, b = 1.75
c = (a + b) / 2
= (1.5 + 1.75) / 2 is 1.625
f(c) = (1.625)³ + (1.625)² - 10(1.625) + 8 is -0.2141
Since f(c) has a negative value, the root lies in the interval [1.625, 1.75].
Iteration 4: a = 1.625, b = 1.75
c = (a + b) / 2
= (1.625 + 1.75) / 2 is 1.6875
f(c) = (1.6875)³ + (1.6875)² - 10(1.6875) + 8 which gives 0.3887.
Since f(c) has a positive value, the root lies in the interval [1.625, 1.6875].
Iteration 5: a = 1.625, b = 1.6875
c = (a + b) / 2
= (1.625 + 1.6875) / 2 is 1.65625
f(c) = (1.65625)³ + (1.65625)² - 10(1.65625) + 8 is 0.0873 .
Since f(c) has a positive value, the root lies in the interval [1.625, 1.65625].
Iteration 6: a = 1.625, b = 1.65625
c = (a + b) / 2
= (1.625 + 1.65625) / 2 which gives 1.640625
f(c) = (1.640625)³ + (1.640625)² - 10(1.640625) + 8 which gives -0.0638.
Since f(c) has a negative value, the root lies in the interval [1.640625, 1.65625].
teration 7: a = 1.640625, b = 1.65625
c = (a + b) / 2
= (1.640625 + 1.65625) / 2 results to 1.6484375
f(c) = (1.6484375)³ + (1.6484375)² - 10(1.6484375) + 8 is 0.0116
Since f(c) has a positive value, the root lies in the interval [1.640625, 1.6484375].
Continuing this process, we can narrow down the interval further until we reach the desired level of accuracy.
b. Newton-Raphson Method: The Newton-Raphson method requires an initial estimate for the root. Let's choose x₀ = 1.5 as our initial estimate.
Iteration 1:
x₁ = x₀ - (f(x₀) / f'(x₀))
f(x₀) = (1.5)³ + (1.5)² - 10(1.5) + 8 which gives -1.375.
f'(x₀) = 3(1.5)² + 2(1.5) - 10 which gives -1.25.
x₁ ≈ 1.5 - (-1.375) / (-1.25) which gives 2.6.
Continuing this process, we can iteratively refine our estimate until we reach the desired level of accuracy.
c. Secant Method: The secant method also requires two initial estimates for the root. Let's choose x₀ = 1.5 and x₁ = 2 as our initial estimates.
Iteration 1: x₂ = x₁ - (f(x₁) * (x₁ - x₀)) / (f(x₁) - f(x₀))
f(x₁) = (2)³ + (2)² - 10(2) + 8 gives 4
f(x₀) = (1.5)³ + (1.5)² - 10(1.5) + 8 gives -1.375
x₂ ≈ 2 - (4 * (2 - 1.5)) / (4 - (-1.375)) gives 1.7826
Continuing this process, we can iteratively refine our estimates until we reach the desired level of accuracy.
To know more about Bisection Method visit-
brainly.com/question/32563551
#SPJ11
a: b = 7:4
b: c= 2:5
Work out a:c
Give your answer in its simplest form.
+
Answer: a: c=
Answers
b:c=2:5=4:10
a:c=7:10
– 1,4, – 9, 16, – 25, ..?
Answers
Answer:
Send me a clarity question.
Answer\((-1)^{x}\)×\(x^{2}\)
Step-by-step explanation:
4. (5 pts) Factor fully. (-8x - 16)(x² - x - 2)² + (4x²+ 16x)(2)(x²-x-2)(2x - 1)
Answers
The fully factored expression is:
8(x² - x - 2)(-x² - 4x - 3)
First, we can simplify (4x²+ 16x)(2) by factoring out 4x:
(4x²+ 16x)(2) = 8x(2x + 1)
Next, we can factor (-8x - 16) by factoring out -8:
(-8x - 16) = -8(x + 2)
Now our expression can be written as:
-8(x + 2)(x² - x - 2)² + 8x(2x + 1)(x² - x - 2)(2x - 1)
We can factor out 8 from both terms to get:
8[-(x + 2)(x² - x - 2)² + x(2x + 1)(x² - x - 2)(2x - 1)]
Now we can see that both terms have a common factor of (x² - x - 2). We can factor this out to get:
8(x² - x - 2)[-(x + 2)² + x(2x + 1)(2x - 1)]
Now we can simplify the expression inside the square brackets:
-(x + 2)² + x(2x + 1)(2x - 1)
= -(x + 2)² + 4x² - 1
= -x² - 4x - 3
So our fully factored expression is:
8(x² - x - 2)(-x² - 4x - 3)
Learn more about factored here:
https://brainly.com/question/14549998
#SPJ11
Numbers assigned to the values of nominal variables are The values assigned to ordinal variables can be meaningfully on some dimension from high to low. A researcher wants to assess the age of their participants and asks each participant to select the category that corresponds to their age (0−16,17−19,20−24,25−29,30−34,35−39,40+). What is the level of measurement of age? Nominal Ordinal Interval Ratio
Answers
The actual numerical differences or intervals between the categories may not be equal or well-defined. Therefore, the measurement level is ordinal.
The level of measurement for the given age categories (0-16, 17-19, 20-24, 25-29, 30-34, 35-39, 40+) is ordinal.
In an ordinal scale of measurement, the values assigned to variables have a meaningful order or ranking. In this case, the age categories are arranged in a specific order, from the youngest (0-16) to the oldest (40+). This order represents a meaningful progression of age groups. However, the actual numerical differences or intervals between the categories may not be equal or well-defined. Therefore, the measurement level is ordinal.
Learn more about actual numerical here
https://brainly.com/question/33422528
#SPJ11
What is the average speed of the car if it covers 400 km in 8 hours?
Answers
An object's average speed is a measurement of how quickly it moves over a predetermined amount of time. The calculation is done by dividing the overall distance travelled by the overall travel time. In other words, it reveals the average amount of distance an object has travelled per unit of time.
In the case provided, we can apply the following calculation to get the average speed of the car:
average speed = total distance / total time
In this instance, a total of 400 kilometers was travelled and 8 hours were expended.
average speed = 400 km / 8 hours
= 50 km/h
This means that the average speed of the car is 50 kilometers per hour. This is the average speed at which the car traveled over the 8 hour period. It does not necessarily mean that the car was traveling at exactly 50 km/h for the entire 8 hour period, It could have gone faster or slower at different times, but on average it traveled at 50 km/h.
Therefore ,average speed of the car is 50 km/h .
To know more about average speed at :
brainly.com/question/4931057
#SPJ4
A _____ measures the dispersion around the expected value.
A. standard deviation
B. mean
C. coefficient of variation
D. chi square
Answers
The correct answer is A. Standard deviation measures the dispersion or variability around the expected value or mean of a data set. It is a commonly used statistical measure to quantify the spread of data points.
Standard deviation is calculated by taking the square root of the variance. The variance is the average of the squared differences between each data point and the mean. By squaring the differences, negative values are eliminated, ensuring that the measure of dispersion is always positive.
A higher standard deviation indicates greater variability or dispersion of data points from the mean, while a lower standard deviation suggests that the data points are closer to the mean.
On the other hand, the mean (option B) is a measure of central tendency that represents the average value of a data set. It does not directly measure the dispersion or variability around the mean.
The coefficient of variation (option C) is a relative measure of dispersion that is calculated by dividing the standard deviation by the mean. It is useful for comparing the relative variability between different data sets with different scales or units.
The chi-square test (option D) is a statistical test used to determine if there is a significant association between categorical variables. It is not a measure of dispersion around the expected value.
For more such questions on standard deviation.
https://brainly.com/question/24298037
#SPJ8
18.
The perimeter of a rectangle is 42 inches. The length of the rectangle can be represented by x + 4 and its width can be represented by 2x minus 7. What is the width of the rectangle in inches?
8
9
12
10.3
Answers
p=2(l+b) =2(3x-3) =6x=48=x=8
Answer: It’s 8
Step-by-step explanation:
Find the Value of y. 70 60 65 40

Answers
Answer:
125
Step-by-step explanation:
360-70-60-65-40
= 125
Answered by GAUTHMATH
Toni goes to a department store and buys two shirts marked the same price. She pays full price for the first shirt but gets a 40% discount on the second shirt. If she pays a total of $32.40 for the two shirts, how much did she pay for the second shirt? -Please give a real answer
Answers
Answe$12.15
Step-by-step explanation:
She paid 60% of the price...
x + .6x = 32.40
1.6x = 32.40
x=20.25
20.25 * .60 = 12.15
9 didvided by 5 and 1 /7th
Answers
Answer:
7/4
Step-by-step explanation:
i am sooo sure that the answer is 1.75
Please answer with full steps. Thanks a lot.
1 If f(x) = (1 + arctan x)3() where g(x) = = then the left hand limit off at 0 Select one: O a. None of them O b. is - O c. is too O d. is 0
Answers
The left-hand limit of g(x) at 0 for the given function, f(x) = (1 + arctan x)3() is 0.
First, we need to find the expression for g(x) in terms of f(x).
From the given information, we know that f(x) = (1 + arctan x)^3.
Let's simplify this expression:
f(x) = (1 + arctan x)^3
= (1 + arctan x)(1 + arctan x)(1 + arctan x)
= (1 + 3arctan x + 3(arctan x)^2 + (arctan x)^3)
Now, we need to find g(x), which is defined as g(x) = f(x) - f(-x).
So,
g(x) = f(x) - f(-x)
= [(1 + 3arctan x + 3(arctan x)^2 + (arctan x)^3)] - [(1 + 3arctan(-x) + 3(arctan(-x))^2 + (arctan(-x))^3)]
= [(1 + 3arctan x + 3(arctan x)^2 + (arctan x)^3)] - [(1 - 3arctan x + 3(arctan x)^2 - (arctan x)^3)]
= 6arctan x - 2(arctan x)^3
Now, we need to find the left-hand limit of g(x) as x approaches 0.
To do this, we can simply substitute x = 0 into the expression for g(x):
lim x→0- g(x) = lim x→0- [6arctan x - 2(arctan x)^3]
= 6arctan 0 - 2(arctan 0)^3
= 0
To know more about left-hand limit, visit:
https://brainly.com/question/24152614
#SPJ11
is it possible to choose (2n 1)^2 points in the disc of radius n such that the distance between any two of them is greater than 1?
Answers
Answer: its (4f 5) ^3
Step-by-step explanation: