a recipe for make 2 dozen muffins requires 1 1/2 cups. how many cups of flour are required per dozen
Answers
Answer:
0.75 or 3/4 is the answer of this question.Step-by-step explanation:
I hoped that helps u...
Thank you ☺️☺️☺️
Related Questions
A survey asked a random sample students if they estimated they spent more or less than an hour a day on social media.

Answers
45 percent of the 8th graders estimated they spend less than an hour a day on social media. The solution has been obtained by using concept of frequency.
What is frequency?
The frequency of a specific value in a set of data is how frequently it appears. Typically, we would keep track of data frequency in a frequency table.
We are given that 17 8th graders spent more than an hour a day on social media and 14 8th graders spent less than an hour a day on social media.
The total 8th graders who spent time on social media is 14 + 17 = 31
The percentage of the 8th graders estimated they spend less than an hour a day on social media is
= 14*100/31
= 45.16%
= 45%
Hence, 45 percent of the 8th graders estimated they spend less than an hour a day on social media.
Learn more about frequency from the given link
https://brainly.com/question/16148316
#SPJ1
Hailey, Priya, and Shetal are auditioning for the same role. Hailey auditions at 10 minutes before four, Priya auditions 30 minutes before Hailey, and Shetal auditions at 5 minutes before four. Order the three by who will audition first.
(pleaseeee show work)
Answers
Answer:
Priya, Hailey, Shetal
Step-by-step explanation:
We know Hailey auditioned 10 mins before 4, so thats 3:50
If Priya auditioned 30 mins before Hailey, that means she auditioned at 3:20
Shetal auditioned 5 mins before 4, so thats 3:55
So the order is Priya, Hailey, Shetal
ABC is a straight line. Work out the size of the angle marked x

Answers
Answer:
x = 57°
Step-by-step explanation:
angles on a straight line add up to 180°. to work out x, we need to subtract 70 and 53 from 180, to get the remaining angle, aka angle x. 180-70=110.
110-53= 57. therefore, x = 57°.
The measure of angle x in the straight line ABC is 57 degrees
What is an equation?An equation is an expression that shows the relationship between two or more numbers and variables.
From the diagram:
x + 53 + 70 = 180° (sum of angles in a straight line).
Hence:
x = 57°
The measure of angle x in the straight line ABC is 57 degrees
Find out more on equation at: https://brainly.com/question/2972832
Help pls for I will give u brainlest

Answers
Answer:
y = 3.5x
Step-by-step explanation:
y=mx+b. given the points (0,0) and (2,7), you solve using y2-y1 / x2-x1 to find slope. This equals 7/2 which = 3.5. Then just put it into equation form of y=mx+b. But, our b is 0 so your equation just becomes y=3.5x
Find the value of x. Write your answer in simplest form.

Answers
See the workup in photo below.
The positive GCF of -24y and -20 is 4. Complete each equation with an expression or integer factor.
Answers
The missing factor in the second equation is 1, and the completed equation is: -24y + (-5) = -4(6y + 5/4)
How to complete each equation with an expression or integer factor.We know that the GCF of -24y and -20 is 4. To find the missing factor in each equation, we can divide both terms by the GCF of 4.
For the first equation, we have:
-24y = 4 * (-6y)
Dividing both sides by 4, we get:
-6y = -24/4
Simplifying, we get:
-6y = -6
Therefore, the missing factor in the first equation is -1, and the completed equation is:
-24y + 20 = -4(6y - 5)
For the second equation, we have:
-20 = 4 * (-5)
Dividing both sides by 4, we get:
-5 = -20/4
Simplifying, we get:
-5 = -5/1
Therefore, the missing factor in the second equation is 1, and the completed equation is:
-24y + (-5) = -4(6y + 5/4)
Learn more about GCF at https://brainly.com/question/219464
#SPJ1
water makes up about 71% of the earth's surface, while the other 29% consists of continents and islands. 96% of all the earth's water is contained within the oceans as salt water, while the remaining 4% is fresh water located in lakes, rivers, glaciers, and the polar ice caps. if the total volume of water on earth is 1,386 million cubic kilometers, what is the volume of salt water in million cubic kilometers?
Answers
The volume of salt water in million cubic kilometers would be: 1330.56 million cubic meters.
How to calculate the volume of salt waterFrom the figures given, we are first told that the total volume of water on earth is 1386 million cubic kilometers. 96% of this figure is salt water. So, to know the exact amount this constitutes from the orginal figure, we will do 96% of 1386 million cubic meters.
The result is 1330.56 million cubic meters. So, the total volume of salt water in million cubic meters is 1330.56.
Learn more about percentages here:
https://brainly.com/question/24877689
#SPJ4
Use differentiation to find the gradient of the curve y = (a + bx)² at x = 1
Answers
We can see that equation (1) is quadratic in nature To find the gradient of the given curve, we need to differentiate the equation (1) with respect to x Gradient is given by
Function is \(y = (a + bx)²At x = 1, y = (a + b(1))²⇒ y = (a + b)²\)
Expanding the above equation, we get y = a² + b² + 2abx …(1)
\(dy/dx⇒ d/dx (a² + b² + 2abx)\) …(2)
Taking the derivative of the above equation, we get⇒
\(d/dx (a² + b² + 2abx) = d/dx(a²) + d/dx(b²) + d/dx(2abx)⇒ 0 + 0 + 2ab⇒ 2ab\)
Now, substituting the value of x in equation (2), we getx = 1, gradient = 2ab
We have to differentiate the given function y = (a + bx)² using the differentiation rule.
To find the gradient of the curve, we need to differentiate the above function, which is given as follows;
\(y = (a + bx)²y = (a + bx) (a + bx)\)
By using the product rule of differentiation, we have
\(dy/dx = (a + bx)d(a + bx)/dx + (a + bx)d(a + bx)/dx= (a + bx) * b + (a + bx) * b= 2b(a + bx)\)
Substituting the value of x = 1, we get the gradient of the curve;
\(y' = 2b(a + b)\)
Therefore, the gradient of the curve \(y = (a + bx)² at x = 1 is 2b(a + b)\).
To know more about quadratic visit:-
https://brainly.com/question/22364785
#SPJ11
please help!!! thank you

Answers
Answer:
WX = 18
Step-by-step explanation:
This is just a simple 1:2 congruency.
We know that because side FD is equal to 7 and side XY is equal to 14.
7:14 is the same as 1:2.
Using that logic we can then apply it to side FE.
Multiply 9 by 2 and you'll get your answer of WX = 18.
1. Ben wrote a report on trains.
Author's Reason:
Explain:
Answers
Answer:
Step-by-step explanation:
the answer is 2 because if you subtract and add you will get your and and good luck on the state test 5th 6th and 7th and younger kids.
need help with this question

Answers
The explicit formula for the nth term of the sequence 14,16,18,... is aₙ = 2n + 12.
What is an explicit formula?
The explicit equations for L-functions are the relationships that Riemann introduced for the Riemann zeta function between sums over an L-complex function's number zeroes and sums over prime powers.
Here, we have
Given: the sequence 14,16,18,….
First term a₁ = 14
Common difference d = 16 - 14 = 2
Now, plug the values into the above formula and simplify.
aₙ = a₁ + d( n - 1 )
aₙ = 14 + 2( n - 1 )
aₙ = 14 + 2n - 2
aₙ = 14 - 2 + 2n
aₙ = 2n + 12
Hence, the explicit formula is aₙ = 2n + 12.
To learn more about the explicit formula from the given link
https://brainly.com/question/9859279
#SPJ1
A sequence is defined by the explicit formula an=3n+4. Which recursive formula represents the same sequence of numbers?
Answers
The recursive formula that represents the same sequence of numbers as the explicit formula an = 3n + 4 is an = an-1 + 3, with the initial term a1 = 7.
A recursive formula defines a sequence by expressing each term in terms of previous terms. In this case, the explicit formula an = 3n + 4 gives us a direct expression for each term in the sequence.
To find the corresponding recursive formula, we need to express each term in terms of the previous term(s). In this sequence, each term is obtained by adding 3 to the previous term. Therefore, the recursive formula is an = an-1 + 3.
To complete the recursive formula, we also need to specify the initial term, a1. We can find the value of a1 by substituting n = 1 into the explicit formula:
a1 = 3(1) + 4 = 7
Hence, the complete recursive formula for the sequence is an = an-1 + 3, with the initial term a1 = 7. This recursive formula will generate the same sequence of numbers as the given explicit formula.
Learn more about recursive formula here:
https://brainly.com/question/1470853
#SPJ11
can somebody teach me how to do this 1 math question, its about solve for the area! WILL Give Brainiest!

Answers
Answer:
area is 100m bc u do 10 times 10
Step-by-step explanation:
Answer:
139.27 meters squared
Step-by-step explanation:
So what you're doing is calculating the square's area and half of the circle's area.
The square's area is 100m^2 since 10*10=100
For the circle part, you use πr^2. You know the diameter of the circle, and radius is half of the diameter, so 10/2=5.
π*5^2 = 78.54 m^2
Since you have half of a circle you divide this by 2.
39.27
Finally you add your two areas together
100+39.27=139.27 meters ^2
Prove the identity a p(p−1) ≡ 1 (mod p 2 ), where a is coprime to p, and p is prime. (Hint: Try to mimic the proof of Fermat’s Little Theorem from the notes.)
Answers
To prove this identity, we start with Fermat's Little Theorem, which states that if p is a prime number and a is any integer coprime to p, then a^(p-1) ≡ 1 (mod p).
Using this theorem, we can rewrite the given identity as a^(p-1) * a(p-2) ≡ 1 (mod p^2).
Next, we can multiply both sides by a to get a^(p-1) * a(p-1) ≡ a (mod p^2).
Since a and p are coprime, we can use Euler's Totient Theorem, which states that a^φ(p) ≡ 1 (mod p) where φ(p) is the Euler totient function. Since p is prime, φ(p) = p-1, so a^(p-1) ≡ 1 (mod p).
Using this result, we can rewrite our identity as a^(p-1) * a(p-1) * a^-1 ≡ a^(p-1) ≡ 1 (mod p), which implies that a^(p-1) ≡ 1 (mod p^2).
Therefore, we have proven the identity a p(p−1) ≡ 1 (mod p 2 ), where a is coprime to p, and p is prime.
Visit here to learn more about Fermat's Little Theorem : https://brainly.com/question/30761350
#SPJ11
Also included below: Unit 5 Review for Edulastic T
Social Networking
Number of
Percent of
Students
Students
35
13
22
10
Independent Work/HW# Show all your steps/process.
SA survey asked students to choose
SA
their favorite social networking website. The result
are shown in the table. Find the percent of students
who chose each site.
Website
Website A
Website B
Website C
Website D
ly and Carolyn were assigned to read a novel with 120 pages.
finished reading 30% of the novel
Answers
The percent of students who chose each website is as follows:
Website A: 29.17%
Website B: 10.83%
Website C: 18.33%
Website D: 8.33%
To find the percent of students who chose each website, you can calculate the percentage for each website by dividing the number of students who chose that website by the total number of students and then multiplying by 100.
Let's calculate the percentages:
For Website A: (35/120) x 100 = 29.17%
For Website B: (13/120) x 100 = 10.83%
For Website C: (22/120) x 100 = 18.33%
For Website D: (10/120) x 100 = 8.33%
So, the percent of students who chose each website is as follows:
Website A: 29.17%
Website B: 10.83%
Website C: 18.33%
Website D: 8.33%
Learn more about Percentage here:
https://brainly.com/question/29306119
#SPJ1
Did I do this right? I’m not sure it this is right

Answers
what is the surface area of a square pyramid with side length 2 yd and slant height 4 yd.
Answers
Answer:
20 yd^2.
Step-by-step explanation:
Area of base = 2^2 = 4 yd^2.
It has 4 side faces so:
Area of each triangular side = 1/2 * 2 * 4 = 4 yd^2
Total surface area = 4 + 4(4).
= 20 yd^2.
the salaries of pharmacy techs are normally distributed with a mean of $32,000 and a standard deviation of $3,000. if 25 pharmacy techs are selected at random, what is the probability their average salary is less than $33,200? the answer should be typed as a decimal with 4 decimal places.
Answers
The probability their average salary is less than $33,200 is = 0.6554
Given that,
Mean = $32,000
Standard deviation = $3,000
The area of mathematics known as probability deals with numerical representations of the likelihood that an event will occur or that a statement is true. An event's probability is a number between 0 and 1, where, roughly speaking, 0 denotes the event's impossibility and 1 denotes certainty.
Standard deviation (SD) is a widely used measurement of variability used in statistics. It shows how much variation there is from the average (mean). A low SD indicates that the data points tend to be close to the mean, whereas a high SD indicates that the data are spread out over a large range of values.
The Z score is used to calculate how many standard deviations above or below the mean the raw score is. It comes from,
z = (x- μ) / σ (Equation-1)
Where,
x=raw score,
μ=mean,
σ=standard deviation
μ=32,000,
σ=3,000
Average salary is less than $33,200
x < 33,200
We can substitute values in Equation-1,
z = (33,200-32,000)/3000
z = 1200/3000
z = 0.4
Using the normal distribution table as a guide,
P(x < 33,200) = P(z < 0.4)
P(x < 33,200) = 1-P(z>0.4)
P(x < 33,200) = 0.6554
Therefore,
The probability their average salary is less than $33,200 is = 0.6554
To learn more about Probability visit:
brainly.com/question/28993703
#SPJ4
The summer and winter solstices are the longest day and night of the year, respectively. The summer solstice happens between June 20 and June 21, while the winter solstice is between December 21 and December 23. At a latitude of 28° the summer solstice is 14.5 hours long and the winter solstice is 14 hours long. Write a sinusoidal equation modeling the hours of daylight in a year. Use t for the variable and measure t in weeks. For the purposes of this problem, idealize a year to be 52 weeks long, with the winter solstice a week before the new year. h(t) = __________
Answers
The correct answer is h(t) = 14.25 + 0.25 * sin((π/26) * t)
To model the hours of daylight in a year using a sinusoidal equation, we can consider the average length of daylight, the amplitude of the variation, and the period of the function.
Given:
Summer solstice (longest day) is 14.5 hours
Winter solstice (longest night) is 14 hours
Let's analyze the information:
Average daylight: The average daylight throughout the year would be the average of the summer and winter solstices. It can be calculated as:
Average daylight = (14.5 + 14) / 2 = 14.25 hours
Amplitude: The difference between the average daylight and the longest day or night is the amplitude. In this case, the amplitude is half the difference between the summer and winter solstices. It can be calculated as:
Amplitude = (14.5 - 14) / 2 = 0.25 hours
Period: We are modeling the function over a year, which we'll consider as 52 weeks. Since we want to measure time in weeks (t), the period of the function is 52 weeks.
Putting all the information together, we can write the sinusoidal equation:
h(t) = Average daylight + Amplitude * sin((2π / Period) * t)
Substituting the values we calculated:
h(t) = 14.25 + 0.25 * sin((2π / 52) * t)
Simplifying further, the sinusoidal equation modeling the hours of daylight in a year is:
h(t) = 14.25 + 0.25 * sin(π/26 * t)
Learn more about function here:
https://brainly.com/question/11624077
#SPJ11
How is graphing a two-variable inequality similar to graphing a one-variable inequality on the number line? HURRY PLEASE
Answers
Answer: “The graph of an inequality in two variables is the set of points that represents all solutions to the inequality. A linear inequality divides the coordinate plane into two halves by a boundary line where one half represents the solutions of the inequality. The boundary line is dashed for > and < and solid for ≤ and ≥.”
- https://www.mathplanet.com
Step-by-step explanation:
Isnt this 1/3??????????

Answers
Somone please help I am completely lost...

Answers
The first one says x+2x+4y.
So the first thing you would do is combine like terms.
x and 2x are like terms.
Since x has no number you would have to put a 1 in place for it.
So you would have 1x+2x which would be 3x.
You would then put that together and have 3x+4y.

Find the volume of the cylinder show steps
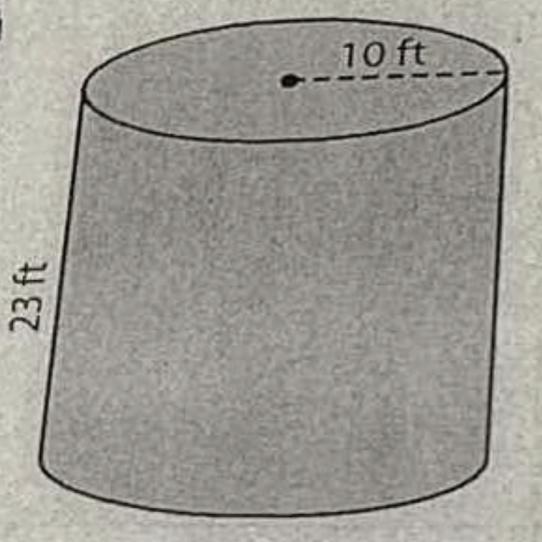
Answers
Answer:
\(\pi *10^{2} *23\) = 7225.66
Step-by-step explanation:
helppppppppp[pppppppppppppppp

Answers
Answer:
D if it's not I do apologize
Which of the following is equivalent to -12 + 3)?
12 + 31
– 12– 3
o 12 – 3
0 12 + 3

Answers
Answer:
\(12 - 3\)
Step-by-step explanation:
\(( - 12 + 3) \\ = 12 - 3 \\ =- 9\)
Hope it is helpful....which equation represents a tangent function with a domain of all real numbers such that where n is an integer?
Answers
The tangent function is defined as the ratio of the sine function to the cosine function. It is periodic with a period of pi and has vertical asymptotes at odd multiples of pi/2. An equation for a tangent function with a domain of all real numbers and n as an integer is given by the following equation:
y = tan(x + n(pi))
The tangent function is defined as the ratio of the sine function to the cosine function, and it is periodic with a period of pi. It has vertical asymptotes at odd multiples of pi/2.
The tangent function can be represented by the following equation:
y = tan(x)
Where x is the angle measured in radians.
If we want to shift the graph of the tangent function by a certain amount, n, in the horizontal direction, we can use the following equation:
y = tan(x + n(pi))
Where n is an integer.
For example, if n = 2, then the graph of the tangent function would be shifted 2pi units to the left, and the equation would be:
y = tan(x - 2pi)
If n = 3, then the graph of the tangent function would be shifted 3pi units to the left, and the equation would be:
y = tan(x - 3pi)
And so on for any integer value of n.
To know more about tangent function: https://brainly.com/question/29117880
#SPJ11
write the expression as a single logarithm log{3} 40 -log{3} 10 show all steps very clearly please
Answers
Answer:
Use the quotient property of logarithms, logb(x)−logb(y)=logb(xy) log b ( x ) - log b ( y ) = log b ( x y ) . log3(4010) log 3 ( 40 10 ). Step 2.
The sum of 24 and 3 times a number y is equal to 56
Answers
Answer:
Step-by-step explanation:
24+3y=56 solve for y, subtract 24 from each side
3y=32 divide each side by 3
y=32/3
Answer:
y=32/3
Step-by-step explanation:
let the number be y, then
24+3y=56 solve for y, subtract 24 from each side
3y=32 divide each side by 3
y=32/3
Find the cost to the nearest cent. $72.95 jacket; 4% tax need help what the answer pls
Answers
+ Sales tax (4%): $ 2.92
Total price including tax: $ 75.87
Solve X^3 = 1/8 A. 1/4 B. 1/2 C. ±1/4 D. ±1/2
Answers
X^3 =(8)^-1
X^3 =(2)^3-1
1/2 is the ans