A linear function and an exponential function are shown below
Over which interval does the growth rate of the exponential function exceed the growth rate of the linear function?
Answers
The interval during which the growth rate of the exponential function exceeds the growth rate of the linear function is from x=0 to x=2.
In general, the growth rate of an exponential function is greater than that of a linear function if the exponential function has a higher rate of change than the linear function. In this case, we can observe that the exponential function has a steeper slope than the linear function over the interval from x=0 to x=2. This means that the exponential function is growing at a faster rate than the linear function during this time period.
To confirm this, we can calculate the rates of change (or slopes) of both functions over this interval. The rate of change of the exponential function is given by its derivative, which is f'(x) = 2^x * ln(2), while the rate of change of the linear function is simply its slope, m = 1. Plugging in x=0 and x=2 into these formulas, we get that the rate of change of the exponential function is approximately 0.693 and 1.386, respectively, while the rate of change of the linear function is a constant 1.
Therefore, we can see that the growth rate of the exponential function exceeds that of the linear function over the interval from x=0 to x=2.
Learn more about exponential function here
https://brainly.com/question/2456547
#SPJ11
Related Questions
55. Joe deposits $500 in to a savings account that grows at a rate of 4.5% annually. If they do not withdraw any money, how much will they have in 3 years?
Answers
After 3 years, Joe will have $579.14 in their savings account if they do not withdraw any money.
To solve the given problem, we need to use the formula for the amount of money in a savings account with compounded interest, which is given by:
A = P(1 + r/n)^(nt), where A is the final amount of money,P is the principal (the initial amount of money deposited),r is the annual interest rate,n is the number of times the interest is compounded per year, and t is the time in years.
Using the given values, we can substitute them into the formula and solve for the final amount of money that Joe will have after 3 years:A = $\(500(1 + 0.045/1)^(^1 ^× 3)A = $500(1.045)^3A\)= $579.14.
Therefore, after 3 years, Joe will have $579.14 in their savings account if they do not withdraw any money.
For more question on withdraw
https://brainly.com/question/24190692
#SPJ8
Aim receive 18 dollar from hi father in a week. The ratio of the amount of money he pend to the amount of money
Answers
As per the given Ratio difference between the amount of money spent and the amount of money saved in a week is $2.
In mathematics, what is a ratio?A ratio is an ordered pair of numbers a and b, denoted by the symbol a / b, where b does not equal zero. A proportion is an equation that sets two ratios equal to each other.
What exactly is the ratio formula?The ratio formula can be used to represent a ratio as a fraction. For any two quantities, say a and b, the ratio formula is a:b = a/b. Because a and b are separate amounts for two portions, the total quantity is given as (a + b).
et 5x be the money he spends and 4x be the amount he saves
therefore, 5x+4x= 18
9x= 18
x= 18/9= 2
Tom spends, 5×2 = $10
and he saves, 4×2= $8
Difference, = $10-$8= $2
Therefore, as per the given ratio in the question difference between the amount of money spent and the amount of money saved in a week is $2.
To know more about ratios visit:
https://brainly.com/question/13419413
#SPJ4
Tom receives $18 from his father in a week. The ratio of the amount of
the money he spends to the amount of money he saves in a week is 5:4
What is the difference between the amount of money spent and
amount of money saved in a week?
I need help with this question please help
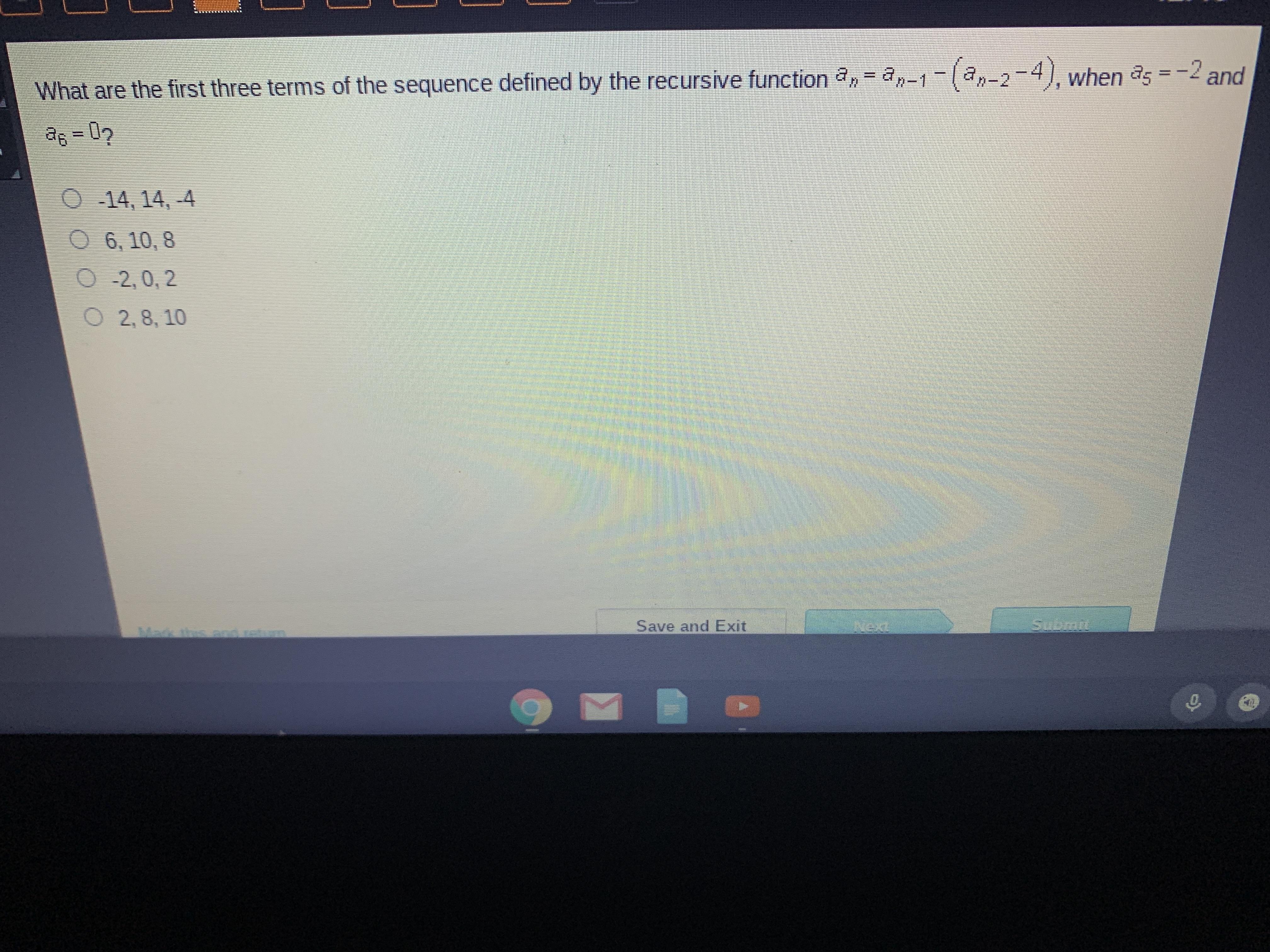
Answers
Answer:
6, 10, 8 is the correct answer.
Step-by-step explanation:
Given that, the recursive function:
\(a_n=a_{n-1}-(a_{n-2}-4)\)
6th term, \(a_{6} =0\)
5th term, \(a_{5} =-2\)
To find:
First three terms of the sequence = ?
Solution:
Putting n = 6 in the recursive function:
\(a_6=a_{5}-(a_{4}-4)\\\Rightarrow 0=-2-(a_{4}-4)\\\Rightarrow 2=-(a_{4}-4)\\\Rightarrow -2=(a_{4}-4)\\\Rightarrow -2+4=a_{4}\\\Rightarrow a_{4}=2\)
Putting n = 5 in the recursive function:
\(a_5=a_{4}-(a_{3}-4)\\\Rightarrow -2=2-(a_{3}-4)\\\Rightarrow -2-2=-(a_{3}-4)\\\Rightarrow 4=(a_{3}-4)\\\Rightarrow a_{3}=8\)
Putting n = 4 in the recursive function:
\(a_4=a_{3}-(a_{2}-4)\\\Rightarrow 2=8-(a_{2}-4)\\\Rightarrow 2-8=-(a_{2}-4)\\\Rightarrow 6=(a_{2}-4)\\\Rightarrow a_{2}=10\)
Putting n = 3 in the recursive function:
\(a_3=a_{2}-(a_{1}-4)\\\Rightarrow 8=10-(a_{1}-4)\\\Rightarrow 8-10=-(a_{1}-4)\\\Rightarrow -2=-(a_{1}-4)\\\Rightarrow 2=a_{1}-4\\\Rightarrow a_{1}=4+2\\\Rightarrow a_{1}=6\)
So, first, second and third terms are 6, 10, 8.
can someone help me out with this problem? Thank you!

Answers
Answer:
three (3).
Step-by-step explanation:
H=O+A
c^2=5^2+12^2
c^2=25+144
c^2=169
c=√169
c=13
\(\qquad\qquad\huge\underline{{\sf Answer}}\)
Let's calculate the value of c using Pythagoras theorem ~
\(\qquad \sf \dashrightarrow \: c {}^{2} = a {}^{2} + {b}^{2} \)
\(\qquad \sf \dashrightarrow \: c {}^{2} = {5}^{2} + {12}^{2} \)
\(\qquad \sf \dashrightarrow \: c = \sqrt{25 + 144} \)
\(\qquad \sf \dashrightarrow \: c = \sqrt{169} \)
\(\qquad \sf \dashrightarrow \: c = 13 \: units\)
please help me on this !

Answers
Answer:
B.) 20
Step-by-step explanation:
We know the midpoint of half of the segment, which is 5. You can use this to find the length of half, after which you can find the entire length by multiplying by 2:
\(RN+NS=RS\\5+5=10\\HR+RS=HS\\10+10=20\)
The length of HS is 20.
Twelve relatives always give gifts to one another. They have been doing it for eight years. How many exchanges have happened so far?
Answers
Answer:
1,056 gifts
Step-by-step explanation:
If twelve relatives give gifts to one another
This means each of the twelve relatives gets gifts from the other 11 relatives
=12 relatives * 11 gifts
= 132 gifts per year
They have been doing it for 8 years
Total gifts exchanged for 8 years= 132 gifts × 8 years
=1,056 gifts
Therefore, number of gifts exchanged for 8 years among 12 relatives is 1,056 gifts
The width of a rectangle is 5 inches. The length of the rectangle is twice the width. Find the perimeter of the rectangle.
PLZZZZZZZZ HELP
Answers
Answer: the perimeter of the rectangle is 30
Step-by-step explanation: so we know that the width of the rectangle is 5. Then it says that the length is two times more than the width....
5 times 2
Which is 10
Now all is left, you find the perimeter (all sides)
5+5+10+10
10+20
30
Therefore,
The perimeter of the rectangle is 30
Answer: 30
Step-by-step explanation: If the width is 5 and the length is twice the width then the length is going to be 10.
p=2(L+W)= 2(10+5)
2 x 15= 30
How many sandwiches could Jonny choose
Bread: white or wheat
Meat: beef, ham, or turkey
Cheese: Swiss or cheddar
Answers
The area of Australia/Oceania is approximately 7.69 × 106 square kilometers. Its population is approximately 3.11 × 107 people. What is the approximate population density (people per square kilometer) of Australia/Oceania? Write your answer in standard form. If necessary, round your answer to the nearest hundredth.
PLEASSSSEEEE HELPPPPPPPPPPP
Answers
Answer: 3.11*10^7/7.69*10^6
3110/769
4.04
Step-by-step explanation:
Pentagon ABCDE and pentagon A″B″C″D″E″ are shown on the coordinate plane below:
Which two transformations are applied to pentagon ABCDE to create A″B″C″D″E″?

Answers
The transformations that are applied to pentagon ABCDE to create A"B"C"D"E" are:
1) Translation (x, y) → (x + 8, y + 2)
2) Reflection across the x-axis (x, y) → (x, -y)
So, the overall transformation given in the graph is (x, y) → {(x + 8), -(y + 2)}.
What are the transformation rules?The transformation rules are:
Reflection across x-axis: (x, y) → (x, -y)Reflection across y-axis: (x, y) → (-x, y)Translation: (x, y) → (x + a, y + b)Dilation: (x, y) → (kx, ky)Calculation:The pentagons in the graph have vertices as
For the pentagon ABCDE: A(-4, 5), B(-6, 4), C(-5, 1), D(-2, 2), and (-2, 4)
For the pentagon A"B"C"D"E": A"(4, -7), B"(2, -6), C"(3, -3), D"(6, -4), and E"(6, -6)
Consider the vertices A(-4, 5) from the pentagon ABCDE and A"(4, -7) from the pentagon A"B"C"D"E".
Applying the Translation rule for the pentagon ABCDE:
The rule is (x, y) → (x + a, y + b)
So, the variation is
-4 + a = 4
⇒ a = 4 + 4 = 8
5 + b = 7
⇒ b = 7 - 5 = 2
So, the pentagon ABCDE is translated by (x + 8, y + 2).
Applying the Reflection rule for the translated pentagon:
The translated pentagon has vertices (x + 8, y + 2).
When applying the reflection across the x-axis,
(x + 8, y + 2) → {(x + 8), -(y + 2)}
Therefore, the complete transformation of the pentagon ABCDE to the pentagon A"B"C"D"E" is (x, y) → {(x + 8), -(y + 2)}
Verification:
A(-4, 5) → ((-4 + 8), -(5 + 2)) = (4, -7)A"
B(-6, 4) → ((-6 + 8), -(4 + 2)) = (2, -6)B"
C(-5, 1) → ((-5 + 8), -(1 + 2)) = (3, -3)C"
D(-2, 2) → ((-2 + 8), -(2 + 2)) = (6, -4)D"
E(-2, 4) → ((-2 + 8), -(4 + 2)) = (6, -6)E"
Learn more about transformation rules here:
https://brainly.com/question/4289712
#SPJ1
The triangles below are similar.

Answers
Answer:
Step-by-step explanation:
Answer:
ΔFGH ~ ΔKLJStep-by-step explanation:
Determine the corresponding sides by the same opposite angles.
Opposite sides to 24° angle are FG and KL.
Correct expression is A:
ΔFGH ~ ΔKLJAn airplane travels 2975 miles in 5 hours. What is the airplane’s average speed?
Answers
Themba lends 12 000 to his friend to buy a car he requires the loan to be repaid after five years with a payment of 22 109,22 . what was the compound interest rate that he charged
Answers
The compound interest rate charged is given as follows:
13% per year.
What is compound interest?The amount of money earned, in compound interest, after t years, is given by:
\(A(t) = P\left(1 + \frac{r}{n}\right)^{nt}\)
In which:
P is the principal, which is the value of deposit/loan/....r is the interest rate, as a decimal value.n is the number of times that interest is compounded per year, annually n = 1, semi-annually n = 2, quarterly n = 4, monthly n = 12.The parameters for this problem are given as follows:
P = 12000, A(t) = 22109.22, n = 1, t = 5.
Hence the interest rate is obtained as follows:
22109.22 = 12000(1 + r)^5
(1 + r)^5 = 22109.22/12000
1 + r = (22109.22/12000)^(1/5)
1 + r = 1.13
r = 1.13 - 1
r = 0.13.
More can be learned about compound interest at https://brainly.com/question/2455673
#SPJ1
The times taken by Amal to run three races were 3 minutes 10 seconds, 2 minutes 58.2 seconds and 3 minutes 9.8 seconds. Find the average time taken, giving your answer in minutes.
Answers
Approximately it is:
3 minutes 19 seconds
Can a line be drawn in the plane that is not a function?
Ο Νο
O Yes
Answers
Answer:if you can draw any vertical line that intersects more than one point on the relationship, then it is not a function.
Step-by-step explanation:So it is a no ok.
Which ratio is equivalent to 3/7
A) 6 to 10
B) 9:21
C) 12/35
D) 7 to 3
Answers
Answer: B 9:21
Step-by-step explanation:
9 reduces to three and 21 reduced to 7
Find all rational roots.
x(3x − 4) (x − 5) = 0
Answers
The rational roots of the given equation x(3x − 4) (x − 5) = 0 are x = 0, 4/3 and 5
What is Rational Number?
Numbers that may be expressed in the form p/q, where p and q are integers and q0, are considered rational numbers. Because fractions cannot have a negative numerator or denominator, they differ from rational numbers in this respect. Because of this, the numerator and denominator of a fraction are whole numbers (denominator 0), unlike in the case of rational numbers, when they are both integers.
So to convert a fractional to reduce form we have to divide by 10 to power how many digits thereafter decimal point, and make sure that numerator or denominator doesn't have common divisible.
x(3x − 4) (x − 5) = 0
So we can put every term equal to zero to find it's root.
1st case, x = 0
2nd, 3x-4 = 0
3x = 4
x= 4/3
3rd, x-5 = 0
x = 5
Hence, the rational roots of the given equation are x = 0, 4/3 and 5
Learn more about Rational Number , by the following link
https://brainly.com/question/12088221
#SPJ1
Mario tracks his heart rate after throwing warm-up pitches before a game. In 1/4 minutes, Mario's heart beats 28 times
Answers
Answer:112
Step-by-step explanation: 1/4 divided by 28/1 = 1/112
Answer:
112 and very light
Step-by-step explanation:

The area of a rectangular patio is 14 5/ 8 square meters. The width of the patio is 3 1/4 meters. What is the length? Enter your answer as a mixed number in simplest form. The length of the patio is meters.
Answers
Answer:
4 1/2 m
Step-by-step explanation:
Area of the patio = 14 5/8 m²
Width = 3 1/4m
Length = ?
Area of the patio = length ×width
Substitute
14 5/8 = 3 1/4 × L
Convert to improper fractions
117/8 = 13/4 L
Cross multiply
8 ×13L = 117×4
2 ×13L= 117
2×L = 9
2L = 9
L = 9/2
L. = 4 1/2 m (in mixed fraction)
PLEASE HELP!!!
WHICH OF THE FOLLOWING FUNCTIONS IS GRAPHED BELOW?

Answers
Answer: D.
Step-by-step explanation:
For an absolute value function, the vertex of \(f(x) = |x+h| + k\) is defined as the point (-h, k) for the coordinate (x, y).
When x is equal to negative h, the value for x and value for h effectively cancel out, and only the positive k remains, hence the vertex being (-h, k).
The function given has a vertex at (2, 3). We know that the vertex of an absolute function is (-h, k), so h must equal -2 and k must equal 3.
The equation:
\(f(x) = |x-2| + 3\)
A wheel makes 20 revolutions each second. Find its approximate velocity in radians per second. A) 20 B) 63 C) 3 D) 7 E) 126
Answers
The velocity to be 40π rad/s. Therefore, the correct option is (E) 40π.
Given that the wheel makes 20 revolutions in one second.
To find the approximate velocity in radians per second we need to use the formula given below.
The formula for velocity is given as:
v = ω * r,
where ω = Angular velocity
r is Radius
The formula for angular velocity is given as:
ω = θ / t
where
θ = Angular displacement
t = Time
Thus the formula for velocity can be written as:
v = (θ / t) * r
On substituting the values, we get:
v = (20 * 2π) / 1
= 40π rad/s
Thus the wheel's approximate velocity in radians per second is 40π rad/s. Hence, the correct answer is 40π .
Conclusion: Wheel makes 20 revolutions in one second. We need to find its approximate velocity in radians per second using the formula
v = ω * r.
On substituting the values, we get the velocity to be 40π rad/s. Therefore, the correct option is (E) 40π.
To know more about velocity visit
https://brainly.com/question/22038177
#SPJ11
Use the geometric series f(x) = 1/1 - x = sigma^infinity_k = 0 x^k, for |x| < 1. to find the power series representation for the following function (centered at 0). Give the interval of convergence of the new series. g(x) = x^3/1 - x Which of the following is the power series representation for g(x)? A. sigma^infinity_k = 0 x^3/x^k C. sigma^infinity_k = 0 1/1 - x^k + 3 B. sigma^infinity_k = 0 x^k + 3 D. sigma^infinity_k = 0 x^3k The interval of convergence of the new series is. (Simplify your answer. Type your answer in interval notation.)
Answers
B. sigma^infinity_k = 0 x^k + 3, and the interval of convergence is (-1, 1).
To find the power series representation for g(x), we need to rewrite g(x) in terms of the given geometric series.
Notice that g(x) can be written as:
g(x) = x^3/1 - x = x^3 * (1/1-x)
We can now substitute the formula for the geometric series to get:
g(x) = x^3 * sigma^infinity_k = 0 x^k
= sigma^infinity_k = 0 (x^3 * x^k)
= sigma^infinity_k = 0 x^(k+3)
Therefore, the power series representation for g(x) is:
sigma^infinity_k = 0 x^(k+3)
The interval of convergence of this series is the same as that of the geometric series, which is |x| < 1.
In interval notation, this can be written as (-1, 1).
Therefore, the correct answer is B. sigma^infinity_k = 0 x^k + 3, and the interval of convergence is (-1, 1).
Know more about convergence here:
https://brainly.com/question/17019250
#SPJ11
Donovan rode 135 miles on his bike at a unit rate of 27 miles per hour. How many hours did he spend riding?
Answers
Answer:
5 HOURS
Step-by-step explanation:
Answer:
5 hours
Step-by-step explanation:
f(x) is a function true or false
Answers
Answer:
Depends on the x value
Step-by-step explanation:
f(x) can only be a function if the x values are not repeating.
10. (a) Let Y = X₁² + X₁² + ... + Xn², where the X;'s are independent Gaussian (0, 1) random variables with PDF fx(x) = (1 / sqrt(2phi)) e^-x²/2. Then Y is known to be a = 2πT chi-squared random variable with n degrees of freedom. Find the MGF of Y, øy (s).
(b) Let S = Y₁ + Y₂ + ··· + Yk, where the Y's are independent random variables, with Y; be a chi-squared random variable with n; degrees of freedom. Show that S is a chi-squared random variable with n₁ + n₂ + ... + nk degrees of freedom.
Answers
S is a chi-squared random variable with n₁ + n₂ + ... + nk degrees of freedom.
Let Y = X₁² + X₁² + ... + Xn², where the X;'s are independent Gaussian (0, 1) random variables with PDF fx(x) = (1 / sqrt(2phi)) e^-x²/2.
Then Y is known to be a = 2πT chi-squared random variable with n degrees of freedom.
To find the MGF of Y, øy (s), we need to follow the given below steps:øy (s) = E [e^sY]øy (s) = E [exp (s (X1² + X2² + ... + Xn²))]øy (s) = E [exp (sX1²) * exp (sX2²) * ... * exp (sXn²)]
Here, the Xs are independent Gaussian variables, so they have characteristic functionsøy (s) = [øx (s)]nøy (s) = [(1 - 2is)⁻¹/2]nøy (s) = [1 - 2is]⁻n/2
The MGF of Y is øy (s) = [1 - 2is]⁻n/2.(b)
Let S = Y₁ + Y₂ + ··· + Yk, where the Y's are independent random variables, with Y; be a chi-squared random variable with n; degrees of freedom.
To show that S is a chi-squared random variable with n₁ + n₂ + ... + nk degrees of freedom, we need to follow the given below steps
We know that MGF of chi-squared random variable with n degrees of freedom is [1 / (1 - 2t)]n.So, for each Yi, the MGF is [1 / (1 - 2t)]n.
When S = Y1 + Y2 + ... + Yk, the MGF of S isøs (t) = øy1 (t) øy2 (t) ··· øyk (t)Putting the MGF of each Yi, we haveøs (t) = [1 / (1 - 2t)]n1 [1 / (1 - 2t)]n2 ··· [1 / (1 - 2t)]nkøs (t) = [1 / (1 - 2t)]n1 + n2 + ... + nk∴ S is a chi-squared random variable with n₁ + n₂ + ... + nk degrees of freedom.(b)
Summary: S is a chi-squared random variable with n₁ + n₂ + ... + nk degrees of freedom.
learn more about variable click here:
https://brainly.com/question/28248724
#SPJ11
(Show your working) I uploaded the question

Answers
x^2 = the first integer
(x - 1)^2 = the second integer.
x^2 - (x - 1)^2 = ?
First, let's plug a number into our equation for x.
(2)^2 - (2 - 1)^2 = ?
4 - (1)^2 = ?
4 - 1 = 3
As we can see the difference is odd but it's also the sum of the two consecutive integers.
2 + 1 = 3.
This works for all numbers. Let's plug another number into our equation for x.
(4)^2 - (4 - 1)^2 = ?
16 - (3)^2 = ?
16 - 9 = 7
4 + 3 = 7
Try any number and it will always be odd.
Please help me!!!!!!!
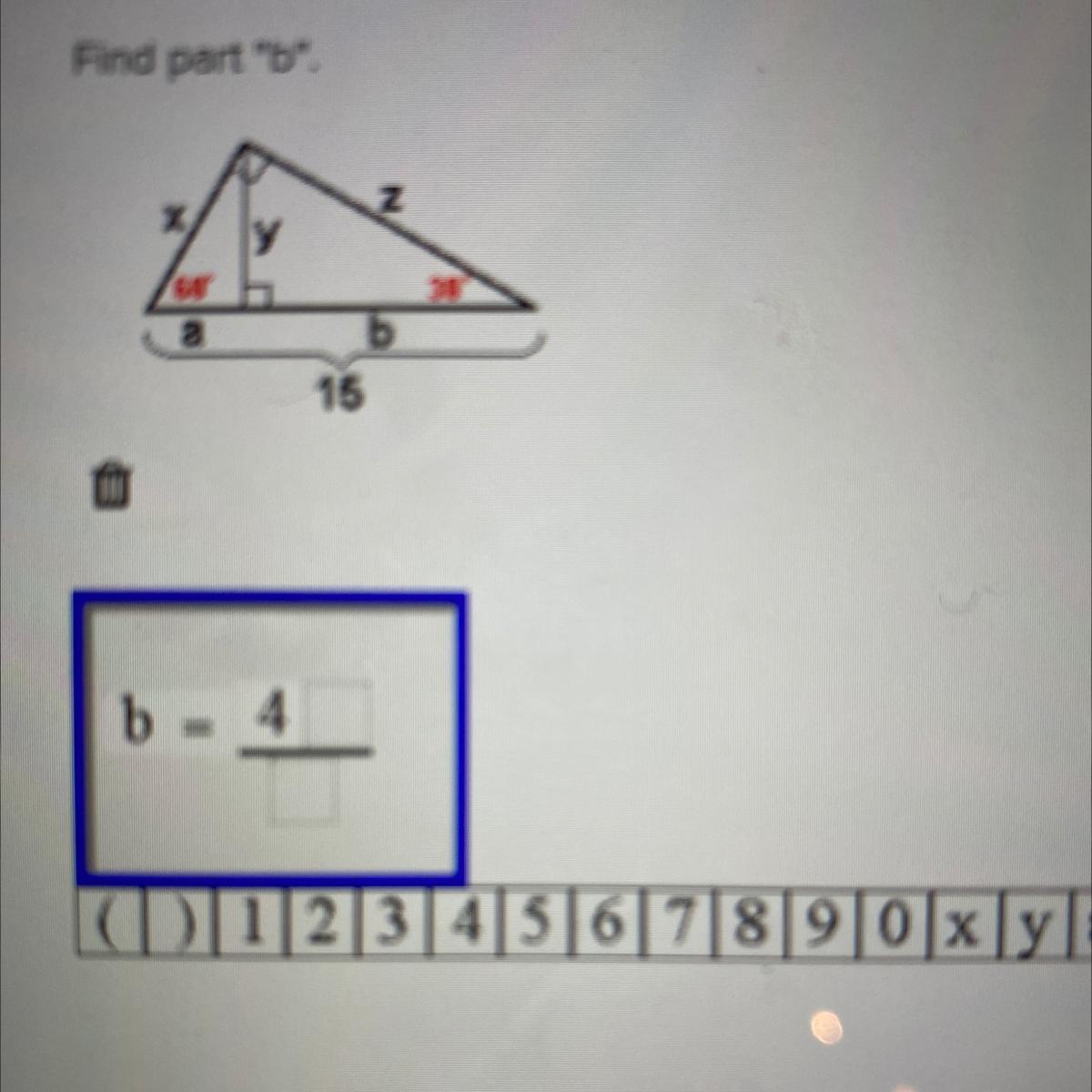
Answers
Answer:
b = 11\(\frac{1}{4}\) (or 11.25)
Step-by-step explanation:
From the diagram,
b = 15 - a
Since the triangles in the figure are all right angled, apply the appropriate trigonometric function to first determine x. We have;
Sin θ = \(\frac{opposite}{hypotenuse}\)
Sin 30 = \(\frac{x}{15}\)
x = Sin 30 x 15
= 7.5
x = 7.5
To determine a,
Cos θ = \(\frac{adjacent}{hypotenuse}\)
Cos 60 = \(\frac{a}{7.5}\)
a = cos 60 x 7.5
= 3.75
a = 3.8
b = 15 - 3.75
= 11.25
b = 11\(\frac{1}{4}\)
Find "both answers.
The answer to the different" question is
The answer to the same three questions is

Answers
The slope of the line is 3
The difference between the consecutive term of the sequence is (1, 3)
To get the slope of the graph, we will use the coordinate points (2, 10) and (3, 13)
Slope = 13-10/3-2
Slope = 3/1
Slope = 3
Hence the slope of the line is 3
The difference in the term for the x-coordinate is given as:
x = 3 - 2 = 4 - 3 = 5 -4 = 1The difference in the term for the y-coordinate is given as:
x = 13 - 10 = 16 - 13 = 19 -16 = 3Hence the difference between the consecutive term of the sequence is (1, 3)
Learn more about slope at: https://brainly.com/question/19417700
The measure of the largest angle of a triangle is 10 more than 4 times the measure of the smallest angle. The measure of another angle is
20° more than the smallest angle.
What is the measure of the largest angle of the triangle?
Answers
the measure of the largest angle of the triangle is Largest angle = 4x + 10 = 4(25) + 10 = 110 So, the largest angle of the triangle has a measure of 110 degrees.
tLet x be the measure of the smallest angle of the triangle.
According to the problem statement, the measure of the largest angle of the triangle is 10 more than 4 times the measure of the smallest angle. Therefore, we can write:
Largest angle = 4x + 10
The measure of another angle is 20° more than the smallest angle. Therefore, we can write:
Other angle = x + 20
Since the sum of the measures of the angles in a triangle is always 180 degrees, we can write an equation based on this fact:
Smallest angle + Largest angle + Other angle = 180
Substituting the expressions we have for the largest angle and the other angle, we get:
x + (4x + 10) + (x + 20) = 180
Simplifying the expression, we get:
6x + 30 = 180
Subtracting 30 from both sides, we get:
6x = 150
Dividing both sides by 6, we get:
x = 25
Therefore, the measure of the largest angle of the triangle is:
Largest angle = 4x + 10 = 4(25) + 10 = 110
So, the largest angle of the triangle has a measure of 110 degrees.
To learn more about triangle click here: brainly.com/question/2773823
#SPJ11
Hi! Please help, if you can :>

Answers
Answer:
I think it's 4/9 the first one