A hall which is 20m long is represented on a diagram as 10cm long. What is the scale of the diagram?
Answers
Answer:
/ 200 ... i think
Step-by-step explanation:
10cm = 10 / 100 = 0.1 m
20 / 0.1 = 200
The scale of the diagram is 0.5cm represents 1 meter.
Here, we have,
To determine the scale of the diagram, we can use the ratio of the length of the hall in reality to its representation on the diagram.
The length of the hall in reality is given as 20m.
The length of the hall on the diagram is given as 10cm.
To find the scale, we need to determine how many centimeters on the diagram correspond to one meter in reality.
Let's set up the proportion:
20m / 10cm = 1m / x
Cross-multiplying:
20m * x = 10cm * 1m
Simplifying:
20x = 10cm
Now, we can solve for x, which represents the number of centimeters on the diagram that corresponds to one meter in reality:
x = 10cm / 20
x = 0.5cm
Therefore, the scale of the diagram is 0.5cm represents 1 meter.
To learn more on scale factor click:
brainly.com/question/5992872
#SPJ2
Related Questions
Please helpp
1. Students were surveyed and asked if they play lacrosse and/or football. The results are shown below.
What percent of football players also play lacrosse?

Answers
A number is increased by 4 is equal to 38 find the number.
Answers
Answer:
34
Step-by-step explanation:
Step 1: form an equation
n + 4 = 38
Step 2: isolate the variable (n)
n = 38 - 4
Step 3: solve the equation
n = 34
1. (a) The sum of two numbers is 17. The difference between twice the larger number and three times the smaller is 4. Find the numbers
Answers
Answer:
Denoting 2 desired numbers: x and y, then:
x + y = 17
2x = 3y + 4
<=>
x = 17 - y
2*(17 - y) = 3y + 4
<=>
x = 17 - y
34 - 2y = 3y + 4
<=>
x = 17 - y
5y = 30
<=>
y = 6
x = 17 - 6 = 11
Hope this helps!
:)
Two side of a triangle are 26 and 27, while the height to the third side is 25. Find the area of the triangle.
Answers
Based on the information given, the area of the triangle is 291.85.
From the information given,
A = 26
A = 26B = 27
A = 26B = 27C = 25
Firstly, we'll add the sides given and divide them by 2. This will be:
S = (26 + 27 + 25) / 2
S = 78/2
S = 39
Then we will use the formula:
= s(s - a)(s - b)(s - c)
= 39(39 - 26)(39 - 27)(39 - 25)
= 39(13 × 12 × 14)
= 85176
Lastly, we'll find the square root of the value gotten. This will be:
= ✓85176
= 291.85.
Therefore, the area is 291.85.
Learn more about triangles on:
https://brainly.com/question/25760317
pls hurry will mark brainliest

Answers
Answer: 10.9 m
So to find the missing side we can use the pythagorean formula to do this. It must be a right angle triangle if we want to use the formula. So we know two of the side lengths and that, that it has a right angle. Let's do it real quick! The formula is:
c^2=a^2+b^2 (c, the missing side, a is any side, b is the other side length)
So in this one we will find the missing side which is c . . . Place the formula!
c^2 = 7.7^2 + 7.7^2
c^2 = 59.29 + 59.29
c = square root of 118.58
c = 10.89 --> round to nearest tenth is 10.9
Brainliest pwease if I could help you! <3
Answer:
nvm then someone already did the answer
Step-by-step explanation:
adios
q+9p when q=18 and p=4 just the answer not how to solve
Answers
Answer:
The answer would be 54.
Answer:
The answer is 54.
Step-by-step explanation:
(Sorry I have to do this otherwise it will be deleted)
18+36
can anyone help me with this I tried to do it but i got to the wrong answer so i need help.

Answers
To use the quadratic formula, we need to identify the values of a, b, and c.
1. In this case, the equation is 4x² - 3x - 8 = 0, so a = 4, b = -3, and c = -8.
2. x = (-b ±√(b² - 4ac))/2a.
3. x = (3 ±√137)/8.
What is Quadratic Formula?The Quadratic Formula is a mathematical equation used to solve second-degree equations.
To use the quadratic formula, we need to identify the values of a, b, and c in the equation ax² + bx + c = 0.
In this case, the equation is
4x² - 3x - 8 = 0,
so a = 4, b = -3, and c = -8.
Once the values of a, b, and c are known, we can substitute them into the Quadratic Formula:
x = (-b ±√(b² - 4ac))/2a.
In this equation, a = 4, b = -3, and c = -8, so the equation becomes
x = (-(-3) ±√((-3)² - 4(4)(-8)))/2(4).
Simplifying, we get x = (3 ±√(9 + 128))/8.
Finally, solving for x yields x = (3 ±√137)/8.
Therefore, the solution to the equation is
x = (3 ±√137)/8.
For more questions related to equation
https://brainly.com/question/2228446
#SPJ1
384 of the 403 people on a plane are passengers.
The rest of the people on the plane are crew.
What fraction of the people on the plane are crew?
Answers
19/403 of the people on the plane are crew
How to determine the crew fraction?The given parameters are:
Population = 403
Passengers = 384
The number of crew is calculated using:
Crew = 403 - 384
Evaluate
Crew = 19
The fraction of crew is then calculated using:
Fraction = Crew/Population
This gives
Fraction = 19/403
Hence, 19/403 of the people on the plane are crew
Read more about fractions at:
https://brainly.com/question/11562149
#SPJ1
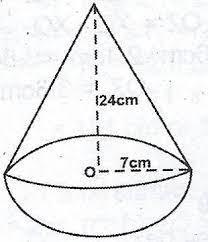
2. The diagram above shows a wooden structure in the form of a cone mounted on hemispherical base. The vertical height of the cone is 24cm and the base 7cm. Calculate correct to 3 significant figures the surface area of the structure. (Take π= 22/7)
Answers
The surface area of the shape is 1166 square meters
How to determine the surface area of the shapeFrom the question, we have the following parameters that can be used in our computation:
Height of cone, h = 24 cm
Radius, r = 7 cm
Also, see attachment for the diagram
The surface area of the shape is calculated as
Surface area = Area of cone + Area of hemisphere
So, we have
Surface area = πr(r + √(r² + h²)) + 3πr²
Substitute the known values in the above equation, so, we have the following representation
Surface area = 22/7 * 7 * (7 + √(7² + 24²)) + 3 * 22/7 * 7²
Evaluate
Surface area = 1166
Hence, the surface area is 1166 square meter
Read more about surface area at
https://brainly.com/question/76387
#SPJ1
Water is coming out of a fountain is modeled by the function f(x)=-x^2+8x+2 where f(x) represents the height, in feet, if the water from the fountain at different times x, in seconds
Answers
PQ= RQ and PS= RS a=?

Answers
The measure of angle a is 15 degrees and this can be determined by using the properties of the isosceles triangle.
What are interior angles?In geometry, interior angles are formed in two ways. One is inside a polygon, and the other is when parallel lines cut by a transversal. Angles are categorized into different types based on their measurements.
Given:
The length of the segment PQ is equal to the length of the segment RQ.The length of the segment PS is equal to the length of the segment RS.The following steps can be used in order to determine the measure of angle a:
Step 1 - According to the given data, it can be concluded that triangle PQR and triangle PSR are isosceles triangles.
Step 2 - Apply the sum of interior angle property on triangle PQR.
\(\angle\text{Q}+\angle\text{P}+\angle\text{R}=180\)
\(\angle\text{Q}+2\angle\text{R}=180\)
\(2\angle\text{R}=180-60\)
\(\angle\text{R}=60^\circ\)
Step 3 - Now, apply the sum of interior angle property on triangle PSR.
\(\angle\text{P}+\angle\text{S}+\angle\text{R}=180\)
\(\angle\text{S}+2\angle\text{R}=180\)
\(2\angle\text{R}=180-90\)
\(\angle\text{R}=45^\circ\)
Step 4 - Now, the measure of angle a is calculated as:
\(\angle\text{a}=60-45\)
\(\angle\text{a}=15\)
The measure of angle a is 15 degrees.
For more information on interior angles, refer to the link given below:
https://brainly.com/question/28795639
The point (3,4) is on a circle centered at (0,0). Which of these points lie on the circle? Select all that apply.
Answers
distance = sqrt((3-0)^2 + (4-0)^2)
= sqrt(9 + 16)
= sqrt(25)
= 5
Since the distance between the point (3, 4) and the center (0, 0) is 5, the radius of the circle must also be 5. Therefore, any point that is a distance of 5 from the center (0, 0) will lie on the circle.
The points that lie on the circle are:
(0 + 5cos(theta), 0 + 5sin(theta))
where theta is the angle between the positive x-axis and the line connecting the center of the circle to the point on the circle. For example, (3,4) corresponds to theta = 53.13 degrees.
The points that lie on the circle are:
(5cos(theta), 5sin(theta))
where theta is the angle between the positive x-axis and the line connecting the center of the circle to the point on the circle. For example, (3,4) corresponds to theta = 53.13 degrees.
If this helps, please five stars. :)
The solution is,
The points that lie on the circle are:
(5cos(theta), 5sin(theta))
where theta is the angle between the positive x-axis and the line connecting the center of the circle to the point on the circle. For example, (3,4) corresponds to theta = 53.13 degrees.
What is circle?A circle is a closed two-dimensional figure in which the set of all the points in the plane is equidistant from a given point called “centre”. The perimeter around the circle is known as the circumference.
here, we have,
A point (x, y) lies on a circle centered at (0, 0) if the distance between the point and the center of the circle is equal to the radius of the circle. We can use the distance formula to find the distance between the point (3, 4) and the center (0, 0):
distance = sqrt((3-0)^2 + (4-0)^2)
= sqrt(9 + 16)
= sqrt(25)
= 5
Since the distance between the point (3, 4) and the center (0, 0) is 5, the radius of the circle must also be 5.
Therefore, any point that is a distance of 5 from the center (0, 0) will lie on the circle.
so, we get,
The points that lie on the circle are:
(0 + 5cos(theta), 0 + 5sin(theta))
where theta is the angle between the positive x-axis and the line connecting the center of the circle to the point on the circle. For example, (3,4) corresponds to theta = 53.13 degrees.
Learn more about circle here:
brainly.com/question/11833983
#SPJ2
Please help me with this question. the m is 6 and the d is 8

Answers
Step-by-step explanation:
so, we have
6x² + 8xy + 8y²
and
5x² + 3xy + 16y²
we can combine only terms of the same kind (defined by the type and exponent of the used variables).
this is like adding fruit.
e.g. when we have a mixture of 3 apples, 4 oranges and 5 plums, and we add a mixture of 6 apples, 2 oranges and 3 plums - what do we get ?
we get a new mixture of
3+6 = 9 apples
4+2 = 6 oranges
5+3 = 8 plums
and exactly the same thing happens with mixing terms when adding them up.
so, we get
6+5 = 11x²
8+3 = 11xy
8+16 = 24y²
so, the result is
11x² + 11xy + 24y²
it is really that simple.
Re-write the expression in the rational exponent form.

Answers
Answer: If you meant: \(\sqrt{x5}\)
Then, let's change the square t :o read: \(\sqrt[x]{1/2}\) Now, we can just multiply the two powers, and your answer is\(x\frac{5}{2}\)Hope this helps have a awesome day/night❤️✨Total area=
Help me please, thankss

Answers
The Area of given figure is 341.6 square.
According to the statement
we have to find the total area of given figure.
Here a= 10 and h= 11
So, we use the formula is A = a(a + √((a)^2 + 4(h)^2))
where the a represent the base of given solid or sides of the equilateral triangle
And h represent the slant height of the solid.
So, Substitute the values in above formula then
A = 10(10 + √((10)^2 + 4(11)^2))
A = 10(10 + √((100 + 4(121))
A = 10(10 + √(100 + 484)
A = 10(10 + √(584)
A = 10(10 + 24.16)
A = 10(34.16)
A= 341.6
So, The Area of given figure is 341.6 square.
Learn more about AREA here https://brainly.com/question/10090807
#SPJ1
Indicate where each aspect of an index card should be placed when researching. Match the letter that corresponds to one of the items below to the correct location (1,2,3,4,5) on an index card.
A. Page Number
B. Title of card (aspect of subject)
C. Paraphrase
D. Source Number
E. Quotation
Answers
When researching, here is where each aspect of an index card should be placed: Match the letter that corresponds to one of the items below to the correct location (1,2,3,4,5) on an index card.A.
Title of card (aspect of subject) - (2) This should be the center or topmost part of the index card. It should be clear and concise enough to reflect what is contained in the index card.B.
Source Number - (4) This is the number allocated to each source in your reference list.C. Page Number - (3) This refers to the page number(s) where the information was sourced from. It is usually written on the top right or left corner of the index card.D.
Quotation - (1) This refers to the exact words that were used in the source materials and is written verbatim. This is usually written in quotation marks.E.
Paraphrase - (5) This refers to rewording a particular section of information in your own words without changing its meaning. The paraphrase should be accurate, concise, and written in a sentence format.
Learn more about index card
https://brainly.com/question/1331338
#SPJ11
Pls help what is this as a simplified fraction (thank u Jesus loves u)

Answers
(-1 39/100) x (-6 8/10) = -139/100 x -68/10 = 9452/1000 = 2363/250
Please please please give me brainiest!!I just need one more ty
What is the value of the expression below when x = -5 and y = -10
|3x - y| +4
Answers
Answer:
-1 is your answer for this mate
If the interest of a sum of money in 6years is 3 by 8 of the principal what is the rate of interest
Answers
Answer: rate of interest (r) = 6.25
Step-by-step explanation:
Simple interest formula is S.I = PxTxR/100
From the question ;
S.I = (3/8) principal
3/8p = px6xr/100
Eliminate p on both sides of the equation
r = (3x100) / (8 x 6)
r = 300 / 48
r = 6.25
regular expressions r and s. describe algorithm verify l(r) = l(s)
Answers
To verify whether the languages of two regular expressions r and s are equal, we can follow these steps:
Construct the finite automata for r and s.
Convert both the finite automata to their corresponding deterministic finite automata (DFA).
Minimize the DFAs obtained in step 2.
Compare the minimized DFAs to check if they are equivalent.
If the DFAs are equivalent, then the languages of r and s are also equal.
Alternatively, we can directly compare the regular expressions r and s by using the following algorithm:
Convert both r and s to their equivalent minimal deterministic finite automata (DFA).
Construct the product DFA of the two DFAs obtained in step 1.
Check if the accepting states of the product DFA correspond to the same regular expressions in r and s.
If the accepting states correspond to the same regular expressions, then l(r) = l(s). Otherwise, l(r) ≠ l(s).
Note that the above algorithm may not be efficient for larger regular expressions, and in such cases, constructing the minimal DFAs may be a more practical approach.
Learn more about expressions here:
https://brainly.com/question/28170201
#SPJ11
how to solve 1-(-8)- 12/-3
Answers
Answer:
ok so the answer is 13
Step-by-step explanation:
to solve you..
PEMDAS
PLEASE EXUSE MY DEAR AUNT SALLY
1-(-8)-12/-3
1-(-8)+4
1+8+4
9+4
13
!
HOPE THIS HELPED YA
Which graph represents the solution to one seventhm ≤ −1 over 22? number line with closed circle on point negative 14 over 11 and arrow shaded to the right number line with closed circle on point negative 7 over 22 and arrow shaded to the right number line with closed circle on point negative 14 over 11 and arrow shaded to the left number line with closed circle on point negative 7 over 22 and arrow shaded to the left You must check the box below prior to submitting your exam! Check this box to indicate you are ready to submit your exam FDK101.12 Previous QuestionNext Question
Answers
A graph which represents the solution to the given inequality one seventh m ≤ −1 over 22 (m/7 ≤ −1/22) is: D. number line with closed circle on point negative 7 over 22 and arrow shaded to the left.
What is a number line?In Mathematics, a number line can be defined as a type of graph with a graduated straight line which comprises both positive and negative numerical values that are placed at equal intervals along its length.
This ultimately implies that, a number line primarily increases in numerical value towards the right and decreases in numerical value towards the left.
Next, we would solve the given inequality as follows:
m/7 ≤ −1/22
Multiplying both sides by 7, we have:
7 × m/7 ≤ −1/22 × 7
m ≤ −7/22
In conclusion, a solution to the given inequality is either m ≤ −7/22, which is illustrated by the number line shown in the image attached below.
Read more on inequality here: brainly.com/question/3061666
#SPJ1

Multiply.
\(\frac{\sqrt{2}}{6}cis (\frac{3\pi }{5})\)·\(\frac{\sqrt{6}}{4}cis (\frac{2\pi }{3})\)
A.\(\frac{\sqrt{3}}{12}cis(\frac{19\pi }{15})\)
B. \(\frac{\sqrt{3}}{12}cis(\frac{2\pi }{5})\)
C. \(\frac{\sqrt{2}}{8}cis(\frac{2\pi }{5})\)
D. \(\frac{\sqrt{2}}{8}cis(\frac{19\pi }{15})\)
Answers
Multiply the moduli and add the arguments:
√2/6 cis(3π/5) × √6/4 cis(2π/3)
= (√2/6 × √6/4) cis(3π/5 + 2π/3)
= √3/12 cis(19π/15) … [A]
a sock drawer contains 18 black socks and 12 red socks. if you randomly choose two socks at once, what is the probability you get a matching pair?
Answers
There are 12 red socks and 18 black socks in a sock drawer. If you randomly choose two socks at once, the probability you get a matching pair is 50%.
The probability of getting a matching pair of socks can be calculated as follows:
First, we can calculate the total number of ways to choose 2 socks out of 30:
C(30, 2) = 30! / (2! * (30-2)!) = 435
Now, we need to calculate the number of ways to choose 2 socks such that they are both black or both red:
Number of ways to choose 2 black socks: C(18, 2) = 153
Number of ways to choose 2 red socks: C(12, 2) = 66
Therefore, the total number of ways to choose a matching pair of socks is 153 + 66 = 219.
Finally, we can calculate the probability of getting a matching pair of socks by dividing the number of ways to choose a matching pair by the total number of ways to choose 2 socks:
P(matching pair) = 219 / 435 ≈ 0.5034
Therefore, the probability of getting a matching pair of socks is approximately 0.5034 or 50.34%.
To learn more about probability, refer:-
https://brainly.com/question/11234923
#SPJ4
Each exterior angle in a regular polygon has a measure
of 18. How many sides does the polygon have?
O 18
0 20
0 36
O 10
1
2
Answers
Answer:
20
Step-by-step explanation:
20
Step-by-step explanation:
The total exterior angles of the polygon equals to 360°.
360÷18(the size of the angles each side has)
thus answer =20
Please help!!! Eitan randomly selected volcanoes to travel to and study. After traveling, he had seen 13 cinder cone volcanoes,
18 shield volcanoes, and 6 stratovolcanoes.

Answers
Answer:
cinder cone: estimated probability = 0.35
shield: estimated probability = 0.49
stratovolcano: estimated probability = 0.16
Step-by-step explanation:
Given that he had seen 13 cinder cone volcanoes, 18 shield volcanoes, and 6 stratovolcanoes.
So the total number of volcanoes are 13 + 18 + 6 = 37
So the estimated probability of Cinder cone is \frac{13}{37}\approx 0.35
37
13
≈0.35
The estimated probability of Shield is \frac{18}{37}\approx 0.49
37
18
≈0.49
The estimated probability of Stratovolcano is \frac{6}{37}\approx 0.16
37
6
≈0.16
Below is the completed table
Someone help me please want asap

Answers
Answer:
C
Step-by-step explanation:
Trust me bro.
Use the sequence below to complete each task. 3, -15, 75, ... a. Identify the common ratio (r). b. Write an equation to represent the sequence. C. Find the 5th term (as) Algebra), 2013 → B I y Default A A : = 5 川里
Answers
a)
This is a geometric sequence, this means that each value of the sequence is multiplied by the common ratio to determine the next number.
For the sequence {3,-15,75}
Divide one of the given numbers by the number before it on the sequence to determine the common ratio
\(r=\frac{-15}{3}=-5\)The common ratio for this sequence is r=-5
b)
a is the first value of the sequence
r is the common ratio
k is the place on the sequence of the required value
You can calculate said value using
\(ar^k\)c)
For
a=3
r=-5
k=5
The value fo the sequence is
\(ar^k=3(-5)^5=-9375\)find the average value of 1/r^2 over the annulus {(r,theta): 4≤r≤6}
Answers
The average value of \($\frac{1}{r^2}$\) over the annulus \($\{(r,\theta): 4 \leq r \leq 6\}$\).
Given an annulus\($\{(r,\theta): 4 \leq r \leq 6\}$\) we need to find the average value of\($\frac{1}{r^2}$\) over this region. Using the formula for the average value of a function f(x,y) over a region R, we get:
The average value of f(x,y) over the region R is given by: \($\frac{\int_R f(x,y) \,dA}{A(R)}$\)
Here, dA represents the area element and A(R) represents the area of the region R. So, we have: \($f(r,\theta) = \frac{1}{r^2}$\).
We know that \($4 \leq r \leq 6$\) and \($0 \leq \theta \leq 2\pi$\). Therefore, the area of the annulus is given by:\($A = \pi(6^2 - 4^2) = 32\pi$\)
Now, we need to find \($\int_R \frac{1}{r^2} \,dA$\). We know that \($dA = r \,dr \,d\theta$\). Therefore, \($\int_R \frac{1}{r^2} \,dA = \int_0^{2\pi} \int_4^6 \frac{1}{r^2} r \,dr \,d\theta$\)
Simplifying, we get: \($\int_R \frac{1}{r^2} \,dA = \int_0^{2\pi} \left[\ln(r)\right]_4^6 \,d\theta$\). Using the property of logarithms, we have: \($\int_R \frac{1}{r^2} \,dA = \int_0^{2\pi} \ln(6) - \ln(4) \,d\theta$\).
Evaluating the integral, we get: \($\int_R \frac{1}{r^2} \,dA = 2\pi \ln\left(\frac{3}{2}\right)$\).
Now, the average value of \($\frac{1}{r^2}$\) over the annulus is given by:
\($\text{average} = \frac{\int_R \frac{1}{r^2} \,dA}{A}$\).
Substituting the values, we get:.
Simplifying, we get: \($\text{average} = \frac{\ln\left(\frac{3}{2}\right)}{16}$\).
Therefore, the average value of\($\frac{1}{r^2}$\) over the annulus \($\{(r,\theta): 4 \leq r \leq 6\}$\) is \($\frac{\ln\left(\frac{3}{2}\right)}{16}$\).
Thus, we have found the average value o f\($\frac{1}{r^2}$\) over the annulus \($\{(r,\theta): 4 \leq r \leq 6\}$\).
To know more about average value, click here
https://brainly.com/question/28123159
#SPJ11
An assembly line has 16 hours to make 1.000 units. What is the required cycle time? (slide 23) 72sec 216sec 57.65sec 14,4sec
Answers
The required cycle-time is approximately 57.6 seconds.
To find the required cycle time, we need to divide the total available time by the number of units to be produced.
Total available time: 16 hours = 16 * 60 minutes = 960 minutes = 960 * 60 seconds = 57,600 seconds
Number of units to be produced: 1,000 units
Required cycle time: Total available time / Number of units
Cycle time = 57,600 seconds / 1,000 units
Cycle time ≈ 57.6 seconds
Therefore, the required cycle time is approximately 57.6 seconds.
Learn more about cycle-time from the given link
https://brainly.com/question/15356513
#SPJ11