The volume (in cubic feet) of a black cherry tree can be modeled by the equation ŷ= - 52.2 +0.4x4 + 5.2x2, where x, is the tree's height (in feet) and xz is the tree's diameter (in inches). Use the multiple regression equation to predict the y-values for the values of the independent variables. (a) x, = 72, X2 = 8.8 (6) X, = 65, X2 = 11.4 (c) X, = 85, X2 = 17.2 (d) x, = 86, X2 = 19.4
a)The predicted volume is ____ cubic feet.(Round to one decimal place as needed.)
b)The predicted volume is ____ cubic feet.(Round to one decimal place as needed.)
c)The predicted volume is ____cubic feet.(Round to one decimal place as needed.)
d)The predicted volume is ____cubic feet.(Round to one decimal place as needed.)
Answers
Therefore, the predicted volumes are: a) 331.81 cubic feet and b) 273.14 cubic feet and c) 613.45 cubic feet and d) 725.64 cubic feet.
The volume (in cubic feet) of a black cherry tree can be modeled by the equation ŷ= - 52.2 +0.4x4 + 5.2x2, where x, is the tree's height (in feet) and xz is the tree's diameter (in inches).
We are supposed to use the multiple regression equation to predict the y-values for the values of the independent variables.
Here, the value of x (height) and x2 (diameter) are given to us.
We will put these values in the equation to get the volume for each given set of values of x and x2.
Now, let's put the values in the equation and calculate the volume.
a) x=72, X2=8.8
ŷ= - 52.2 +0.4(72)4 + 5.2(8.8)2= 331.81 cubic feet.
b) x=65, X2=11.4
ŷ= - 52.2 +0.4(65)4 + 5.2(11.4)2= 273.14 cubic feet.
c) x=85, X2=17.2ŷ= - 52.2 +0.4(85)4 + 5.2(17.2)2= 613.45 cubic feet.
d) x=86, X2=19.4ŷ= - 52.2 +0.4(86)4 + 5.2(19.4)2= 725.64 cubic feet.
Therefore, the predicted volumes are:
a) 331.81 cubic feet.
b) 273.14 cubic feet.
c) 613.45 cubic feet.
d) 725.64 cubic feet.
To know more about regression equation visit:
https://brainly.com/question/32810839
#SPJ11
Related Questions
Determine the approximate angle of sunrise and sunset for February 3 for WPU, NJ, approximate latitude: 40 degrees north. (Use the closest equinox date for calculation).
a) 90 degrees sunrise, 270 degrees sunset
b) 102 degrees sunrise, 258 degrees sunset
c) 78 degrees sunrise, 282 degrees sunset
d) 66.5 degrees sunrise, 293.5 degrees sunset
e) 113.5 degrees sunrise, 246.5 degrees sunset
Answers
The approximate angle of sunrise for February 3 at WPU, NJ, with an approximate latitude of 40 degrees north, would be around 66.5 degrees, and the approximate angle of sunset would be around 293.5 degrees.
To determine the approximate angle of sunrise and sunset for a specific location and date, we can use the knowledge that on the equinox, the sunrise and sunset angles are at their extremes. The equinox occurs around March 21 and September 21. Since we are looking for February 3, which is closer to the March equinox, we can use the values for the March equinox.
On the equinox, the sunrise and sunset angles are approximately 66.5 degrees and 293.5 degrees, respectively. These values correspond to the direction measured clockwise from due north.
Know more about latitude here:
https://brainly.com/question/14833692
#SPJ11
Please help I will make you Brainliest (show working)

Answers
U7L2 Cool Down
The measure of the arc from B to A not passing through C is 26 degrees.
1. What is the measure of angle BOA ?
2. What is the measure of angle BDA?
3. What is the measure of angle BCA ?
degrees
degrees
degrees
Answers
Using the inscribed angle theorems, the measure of the indicated angles are:
1. m∠BOA = 26°
2. m∠BDA = 13°
3. m∠BCA = 13°
What is the Inscribed Angle Theorems?Based on the inscribed angle theorem, the following relationships are established:
Inscribed angle = 2(measure of intersected arc)Central angle = measure of intersected arcGiven:
Intercepted arc BA = 26°
1. ∠BOA is central angle
Thus:
m∠BOA = 26° (inscribed angle theorems)
2. ∠BDA is inscribed angle.
m∠BDA = 1/2(30) = 13° (inscribed angle theorems)
3. m∠BCA = m∠BDA = 13° (inscribed angle theorems)
Learn more about inscribed angle theorems on:
https://brainly.com/question/30494878
a² = 3 and a² - 1 = 1 find the value of a
Answers
Answer:
No solutions to the problem
Step-by-step explanation:
Wolfram Alpha for more info
How do I solve this question ?

Answers
Step-by-step explanation:
here you go!
so basically x = 9 cars

100bbl/ day of oil is flowing in a 2 inch inner diameter wellbore with pipe relative roughness of 0.001. The oil has density of 48lbm/ft 3 and viscosity of 1.8cp. The wellbore is deviated 15 degrees from horizontal flow and has length of 6,000ft. The bottom hole flowing wellbore pressure is 2,200psi.
a) Obtain the potential pressure drop in the wellbore (psi).
b) Determine the frictional pressure drop in the wellbore (psi).
c) If there is also gas flowing in the wellbore at 150ft 3 / day covering 20% of the total pipe volume, calculate the in-situ oil velocity (ft/s).
d) For case (c), determine the flow regime of the two-phase flow.
Answers
a) To obtain the potential pressure drop in the wellbore, we can use the hydrostatic pressure equation.
The potential pressure drop is equal to the pressure gradient multiplied by the length of the wellbore. The pressure gradient can be calculated using the equation: Pressure gradient = (density of oil × acceleration due to gravity) × sin(θ), where θ is the deviation angle of the wellbore from horizontal flow. In this case, the pressure gradient would be (48 lbm/ft^3 × 32.2 ft/s^2) × sin(15°). Multiplying the pressure gradient by the wellbore length of 6,000 ft gives the potential pressure drop.
b) To determine the frictional pressure drop in the wellbore, we can use the Darcy-Weisbach equation. The Darcy-Weisbach equation states that the pressure drop is equal to the friction factor multiplied by the pipe length, density, squared velocity, and divided by the pipe diameter. However, to calculate the friction factor, we need the Reynolds number. The Reynolds number can be calculated as (density × velocity × diameter) divided by the oil viscosity. Once the Reynolds number is known, the friction factor can be determined. Finally, using the friction factor, we can calculate the frictional pressure drop.
c) To calculate the in-situ oil velocity, we need to consider the total volume of the pipe, including both oil and gas. The total pipe volume is calculated as the pipe cross-sectional area multiplied by the wellbore length. Subtracting the gas volume from the total volume gives the oil volume. Dividing the oil volume by the total time taken by the oil to flow through the pipe (converted to seconds) gives the average oil velocity.
d) The flow regime of the two-phase flow can be determined based on the oil and gas mixture properties and flow conditions. Common flow regimes include bubble flow, slug flow, annular flow, and mist flow. These regimes are characterized by different distribution and interaction of the oil and gas phases. To determine the specific flow regime, various parameters such as gas and liquid velocities, mixture density, viscosity, and surface tension need to be considered. Additional information would be required to accurately determine the flow regime in this scenario.
Learn more about viscosity here: brainly.com/question/14004181
#SPJ11
what is the measure of the missing angle?

Answers
Answer:
82 degrees
Step-by-step explanation:
sum of the angles of the triangle = 180 °
first angle is 41°
second one is : 180-123 = 57°
then the measure of the missing angle(x) is : 57+41 +x = 180
x= 180-98 = 82°
Help me PLEASEEE I need help
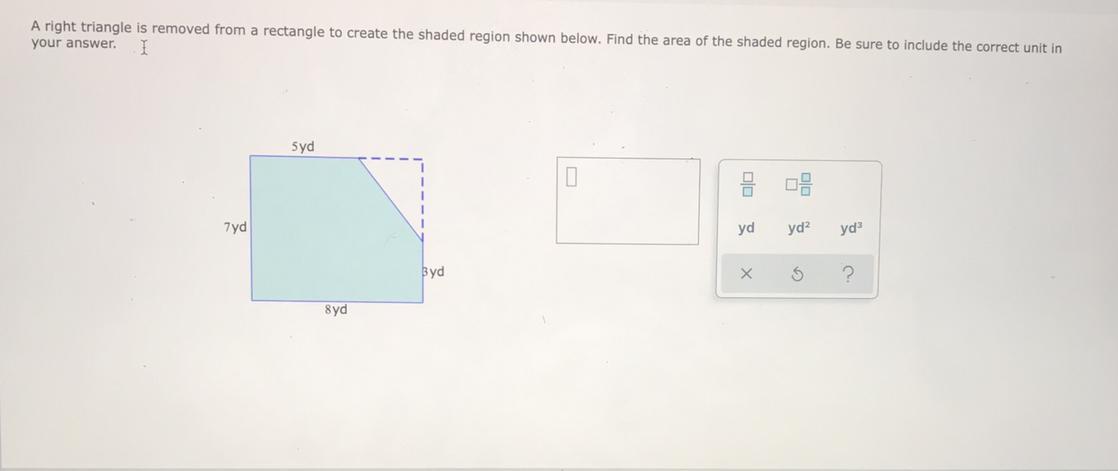
Answers
Answer:
area of shaded portion=56 - 1/2 ×3×4=56-6= 50 yd^2
what is a congruent polygon
Answers
A congruent polygon refers to two or more polygons that have the same shape and size. There must be an equal number of sides between two polygons for them to be congruent.
Congruent polygons have parallel sides of equal length and parallel angles of similar magnitude. When two polygons are congruent, they can be superimposed on one another using translations, rotations, and reflections without affecting their appearance or dimensions. Concluding about the matching sides, shapes, angles, and other geometric properties of congruent polygons allows us to draw conclusions about them.
Learn more about Congruent polygons here:
https://brainly.com/question/2096633
#SPJ1
d(n)d, left parenthesis, n, right parenthesis models the duration (in seconds) of the time it took for hailey to run her n^{th}n th n, start superscript, t, h, end superscript lap. nnn 333 777 999 d(n)d(n)d, left parenthesis, n, right parenthesis 858585 999999 110110110
Answers
The given expression, \(d(n)d(n)d(n)\), represents the duration in seconds for Hailey to run her \(n^{th}\) lap. The specific values provided, 333, 777, 999, correspond to the durations of the 3rd, 7th, and 9th laps, respectively. The values 858585, 999999, and 110110110 are unrelated and do not provide any additional information about lap durations.
The expression \(d(n)d(n)d(n)\) suggests that each lap duration is represented by the function \(d(n)\), where \(n\) denotes the lap number. The specific values given (333, 777, 999) correspond to the 3rd, 7th, and 9th laps, respectively. However, the remaining values (858585, 999999, 110110110) do not appear to have a direct connection to the lap durations or the function \(d(n)\).
Without further information or a specific pattern, it is difficult to interpret the significance of the remaining values. It's important to note that more context or information about the pattern or relationship between the values would be necessary to provide a more detailed explanation or analysis.
Learn more about duration here:
brainly.com/question/32886683
#SPJ11
the fractiions 3/k,4/k ,dand 5/k are in lowest terms. what could be the value of k if the numbers are 48,49,50,51,52?
Answers
The value of k could be 48, 49, 50, 51, or 52, as these all result in the fractions being in lowest terms.
What could be the value of k if the numbers are 48,49,50,51,52?To further explain, let's look at each of the possible values of k and see how they result in the fractions being in lowest terms:
If k = 48, then the fractions are 3/48, 4/48, and 5/48. These can all be simplified to 1/16, 1/12, and 1/9.6, respectively, which are in lowest terms.If k = 49, then the fractions are 3/49, 4/49, and 5/49. These cannot be simplified further, so they are already in lowest terms.If k = 50, then the fractions are 3/50, 4/50, and 5/50. These can all be simplified to 1/16.666..., 1/12.5, and 1/10, respectively, which are in lowest terms.If k = 51, then the fractions are 3/51, 4/51, and 5/51. These can all be simplified to 1/17, 1/12.75, and 1/10.2, respectively, which are in lowest terms.If k = 52, then the fractions are 3/52, 4/52, and 5/52. These can all be simplified to 1/17.333..., 1/13, and 1/10.4, respectively, which are in lowest terms.More information about Lowest terms here: https://brainly.com/question/8933457
#SPJ11
Write the sentence as an inequality.
Ten is at least the product of a number h and 5.
Answers
Answer:
5h ≥ 10
Step-by-step explanation:
5 * h ≥ 10
≥ means greater than or equal to which is recognized in the question for " atleast"
Find x
Help me please

Answers
Answer:
19
Step-by-step explanation:
keiko is on a game show. she will choose a box to see if she wins a prize. the odds in favor of keiko winning a prize are . find the probability of keiko winning a prize.
Answers
Therefore, the probability of Keiko winning a prize is 5/8 or 0.625.
If the odds in favor of Keiko winning a prize are 5 to 3, this means that for every 5 favorable outcomes, there are 3 unfavorable outcomes.
So, the probability of Keiko winning a prize can be calculated as:
P(win) = favorable outcomes / total outcomes
P(win) = 5 / (5 + 3)
P(win) = 5/8
The odds in favor of an event represent the ratio of the number of favorable outcomes to the number of unfavorable outcomes. To convert odds to probability, we divide the number of favorable outcomes by the total number of outcomes (favorable plus unfavorable). In this case, the probability of Keiko winning a prize is 5/8, which means that there is a 5/8 chance that she will win and a 3/8 chance that she will not win.
To know more about probability,
https://brainly.com/question/30034780
#SPJ11
What system of equations would you use to solve the problem below?
The admission fee for an amusement park is $12 for adults and $6.50 for
children. One weekend, 2904 people paid admission for the amusement park,
and the park made $27,126. How many adults and how many children paid to
go to the amusement park that weekend?
O A. a+c= 18,5
12a + 6.5c = 27,126
O B. a+c= 2904
12a + 6.5c = 27,126
O C. a+c= 27,126
12a + 6.5c = 2904
O D. a:c= 2904
12a: 6.5c = 27,126

Answers
Answer: a+c=27,126
Step-by-step explanation:
Here is a set of signed numbers: 7, -3, LaTeX: \frac{1}{2}1 2, -0.8, 0.8, LaTeX: -\frac{1}{10}− 1 10, -2 Order the numbers from least to greatest. Group of answer choices 7, 0.8, 1/2, -1/10, -0.8, -2, -3 -3, -2, -0.8, -1/10, 1/2, 0.8, 7 -1/10, 1/2, -0.8, 0.8, -2, -3, 7
Answers
Answer:
\(-3, -2, -0.8, -\frac{1}{10} ,\frac{1}{2}, 0.8, 7\)
Step-by-step explanation:
Given
\(7, -3, \frac{1}{2}, -0.8, 0.8, -\frac{1}{10}, -2\)
Required
Order from least to greatest
\(7, -3, \frac{1}{2}, -0.8, 0.8, -\frac{1}{10}, -2\)
Convert 1/2 and -1/10 to decimals
\(7, -3, 0.5, -0.8, 0.8, -0.1, -2\)
Negative numbers are always the least of all numbers.
In the given list, the negative numbers are:
\(-3, -0.8, -0.1, -2\)
The higher the magnitude of a negative number, the smaller it is.
--------------------------------------------------------------------------------------------
Take for instance: -7 and -8.
-8 has a magnitude of 8 and -7 has a magnitude of 7.
Because 8 > 7 (the magnitudes), then
-8 < -7
--------------------------------------------------------------------------------------------
Using the above analysis:
\(-3, -0.8, -0.1, -2\) from least to greatest is:
\(-3, -2, -0.8, -0.1\)
Considering the positive numbers:
\(7, 0.5, 0.8\)
From least to greatest, it is:
\(0.5, 0.8, 7\)
Merge the negative and the positive numbers:
\(-3, -2, -0.8, -0.1,0.5, 0.8, 7\)
Convert 0.5 and -0.1 back to fractions
\(-3, -2, -0.8, -\frac{1}{10} ,\frac{1}{2}, 0.8, 7\)
(a) Derive the class equation of a finite group G.
(b) Prove that a Sylow p-subgroup of a finite group G is normal if and only if it is unique.
Answers
a) The center of G and determining the distinct conjugacy classes, we can calculate the class equation of the finite group G.
b) We have shown both implications: if a Sylow p-subgroup is normal, then it is unique, and if it is unique, then it is normal.
(a) Deriving the class equation of a finite group G involves partitioning the group into conjugacy classes. Conjugacy classes are sets of elements in the group that are related by conjugation, where two elements a and b are conjugate if there exists an element g in G such that b = gag^(-1).
To derive the class equation, we start by considering the group G and its conjugacy classes. Let [a] denote the conjugacy class containing the element a. The class equation is given by:
|G| = |Z(G)| + ∑ |[a]|
where |G| is the order of the group G, |Z(G)| is the order of the center of G (the set of elements that commute with all other elements in G), and the summation is taken over all distinct conjugacy classes [a].
The center of a group, Z(G), is the set of elements that commute with all other elements in G. It can be written as:
Z(G) = {z in G | gz = zg for all g in G}
The order of Z(G), denoted |Z(G)|, is the number of elements in the center of G.
The conjugacy classes [a] can be determined by finding representatives from each class. A representative of a conjugacy class is an element that cannot be written as a conjugate of any other element in the class. The number of distinct conjugacy classes is equal to the number of distinct representatives.
By finding the center of G and determining the distinct conjugacy classes, we can calculate the class equation of the finite group G.
(b) To prove that a Sylow p-subgroup of a finite group G is normal if and only if it is unique, we need to show two implications: if it is normal, then it is unique, and if it is unique, then it is normal.
If a Sylow p-subgroup is normal, then it is unique:
Assume that P is a normal Sylow p-subgroup of G. Let Q be another Sylow p-subgroup of G. Since P is normal, P is a subgroup of the normalizer of P in G, denoted N_G(P). Since Q is also a Sylow p-subgroup, Q is a subgroup of the normalizer of Q in G, denoted N_G(Q). Since the normalizer is a subgroup of G, we have P ⊆ N_G(P) ⊆ G and Q ⊆ N_G(Q) ⊆ G. Since P and Q are both Sylow p-subgroups, they have the same order, which implies |P| = |Q|. However, since P and Q are subgroups of G with the same order and P is normal, P = N_G(P) = Q. Hence, if a Sylow p-subgroup is normal, it is unique.
If a Sylow p-subgroup is unique, then it is normal:
Assume that P is a unique Sylow p-subgroup of G. Let Q be any Sylow p-subgroup of G. Since P is unique, P = Q. Therefore, P is equal to any Sylow p-subgroup of G, including Q. Hence, P is normal.
Therefore, we have shown both implications: if a Sylow p-subgroup is normal, then it is unique, and if it is unique, then it is normal.
for such more question on distinct conjugacy
https://brainly.com/question/11583754
#SPJ8
help im new and need help please the thing is 9.9 x 7 =__._ help please
Answers
Answer:
69.3 is the answer
{ Hello and welcome to Brainly :) i hope i helped }
Answer:
69.3
Step-by-step explanation:
Welcome to brainly, I hope you have a good time.
y=3(x-4)^2 +7 in standard form
Answers
Select all the pairs of numbers that have the same greatest common factor (GCF).
16 and 30
26 and 38
12 and 28
22 and 34
24 and 32
Answers
The pairs of numbers that have the same greatest common factor (GCF) is 24 and 32
How can the greatest common factor be known?We can test the given numnbers for their greatest common factor (GCF) For the first option, which 16 and 30, their factor are 16= 2*8, 30 = 2*15, which implies that they do not have the same GCF.
For last option ( 24 and 32) have 8 as their GCF we can see that theeir factors are ; 24= 4*6 = 8*3; 32 =4*8 .Therefore, the last option is correct because they both have the GCF of 8.
Learn more about greatest common factor at:
https://brainly.com/question/219464
#SPJ1
(3squared)squared x(10cubed)squared

Answers
Hii :))
\( \tt {(3 ^{2} )}^{2} \times {(10^{3}) }^{2} \\ \tt = (3 \times 3) ^{2} \times {(10 \times 10 \times 10)}^{2} \\ \tt \: = {9}^{2} \times 1000 ^{2} \\ \tt = (9 \times 9) \times (1000 \times 1000) \\ = \tt \: 81 \times 1000000 \\ = \boxed{\tt \: 81000000}\)
__________________
\(\overbrace{ \underbrace{ \mathfrak{ \: \infty \: Carry \: on \: Learning \: \infty }}}\)
ᴛʜᴇᴇxᴛʀᴀᴛᴇʀᴇꜱᴛʀɪᴀʟ
find a power series representation for the function and determine the interval of convergence. (give your power series representation centered at x = 0.) f(x)=1/(6 x)
Answers
The power series representation of f(x) is f(x) = (1/6) * (1 - x/6 + x²/36 - x³/216 + ...) and centered at x = 0. Also, the interval of convergence for the power series representation.
Understanding Power SeriesThe function f(x) = 1/(6x) can be represented as a power series using the geometric series formula. Recall that the geometric series formula is:
1 / (1 - r) = 1 + r + r² + r³ + ...
In this case, we can rewrite f(x) as:
f(x) = 1/(6x) = (1/6) * (1/x) = (1/6) * (1/(1 - (-x/6)))
Now, we can identify that the function is in the form of a geometric series with a common ratio of -x/6. Therefore, we can use the geometric series formula to write f(x) as a power series:
f(x) = (1/6) * (1/(1 - (-x/6)))
= (1/6) * (1 + (-x/6) + (-x/6)² + (-x/6)³ + ...)
Simplifying the expression:
f(x) = (1/6) * (1 - x/6 + x²/36 - x³/216 + ...)
This is the power series representation of f(x) centered at x = 0.
To determine the interval of convergence, we need to find the values of x for which the power series converges. In this case, the power series is a geometric series, and we know that a geometric series converges when the absolute value of the common ratio is less than 1.
In our power series, the common ratio is -x/6. So, for convergence, we have:
|-x/6| < 1
Taking the absolute value of both sides:
|x/6| < 1
-1 < x/6 < 1
-6 < x < 6
Therefore, the interval of convergence for the power series representation of f(x) is -6 < x < 6.
Learn more about power series here:
https://brainly.com/question/28158010
#SPJ1
How much did Cody deposit every month in his savings account if he had $11,000 after 27 month-end deposits? The money in his savings account was growing at 3.69% compounded monthly. Round to the nearest cent
Answers
Cody deposited approximately $364.54 every month in his savings account.
To calculate the monthly deposit amount, we can use the formula for the future value of an ordinary annuity:
FV = P * ((1 + r)ⁿ - 1) / r
Where:
FV is the future value (the final amount in the savings account)
P is the payment amount (monthly deposit)
r is the interest rate per period (3.69% per annum compounded monthly)
n is the number of periods (27 months)
We need to solve for P, so let's rearrange the formula:
P = FV * (r / ((1 + r)ⁿ - 1))
Substituting the given values, we have:
FV = $11,000
r = 3.69% per annum / 12 (compounded monthly)
n = 27
P = $11,000 * ((0.0369/12) / ((1 + (0.0369/12))²⁷ - 1))
Using a calculator, we find:
P ≈ $364.54
Therefore, Cody deposited approximately $364.54 every month in his savings account.
learn more about future value here
https://brainly.com/question/30787954
#SPJ4
which expression correctly represents six more than the quotient of 3 and a number decreased by 8
Answers
Answer:
6 + 3 Divided by x minus 8.
Step-by-step explanation:
In a state pick 4 lottery game, a bettor selects four numbers between 0 and 9 and any selected number can be used more than onoe. Winning the top prize requires that the selected numbers match those and are drawn in the same order. Do the calculations for this lottery involve the combinations rule or either of the two permutations rules? Why or why not? If not, what rule does apply?
Choose the correct answer below.
A The permutation le with different items applies to his problem because repetit n is allo ed. The mutation rule with some identical items and the c bina rule cannot be used with repetition.
B. The combination and permutations rules do not app y because repetition is allowed and numbers are selected wit replacement. The act al rule apples to his problem
C. The combination and permutations rules do not apply because repetition is allowed and numbers are selected with replacement. The multiplication counting rule applies to this problem.
D. The permutation rule (with some identical items applies to this problem because repetition is allowed. The permutation rule (with different items and the combination rule cannot be used with repetition.
E. The combination rule apples to this problem because the numbers are selected with replacement Neither o the permutations rules a ows replacement.
Answers
The correct option is C. The combination and permutations rules do not apply because repetition is allowed and numbers are selected with replacement. The multiplication counting rule applies to this problem.
With repetition, neither the combination rule nor the mutation rule can be utilized. This is due to the fact that the permutations rule is a rule for taking sets that are not ordered and putting them in a particular order (permutations). The formula for permutations with repetition is nr, where n is the number of options available and r is the number of items you choose. Since order is important in this case, the permutation formula applies and repetition is permitted, so the permutation rule with various items applies to this problem. Since n=10 and r=4, the number of permutations is 104 = 10,000.
Learn more on items here:
brainly.in/question/54158909
#SPJ11
How do I find the slope and Y-intercept of the line x+2y=-2

Answers
slope = -1/2
y-intercept = (0, -1)
Explanation:Given:
\(x\text{ + 2y = - 2}\)To find:
the slope and the y-intercept
To determine the slope we will use the linear function formula:
\(\begin{gathered} y\text{ = mx + b} \\ m\text{ = slope} \\ b\text{ = y-intercept} \end{gathered}\)We need to rewrite the given equation in the form above so as to get the slope
\(\begin{gathered} x\text{ + 2y = -2} \\ 2y\text{ = -x - 2} \\ y\text{ = -}\frac{x}{2}\text{ - }\frac{2}{2} \\ y\text{ = }\frac{-x}{2}-1 \end{gathered}\)From the above, m = -1/2
Hence, the slope is -1/2
The y-intercept is the value of y when x = 0
To get the y-intercept, we will substitute x with 0:
\(\begin{gathered} y\text{ = }\frac{-0}{2}\text{ - 1} \\ y\text{ = 0 - 1} \\ y\text{ = -1} \\ \\ The\text{ y-intercept in ordered pair \lparen x, y\rparen:} \\ when\text{ x = 0, y = -1} \\ y-\text{ intercept = \lparen0, -1\rparen} \end{gathered}\)9) Write the equation of the parabola with vertex ( 5,-4) and concavity-3, determine whether the parabola is concave up or concave down and find the y-intercept:
Answers
The equation of a parabola in vertex form is given by
\(f(x)=a(x-h)^2\text{ + k}\)The vertex (h,k) when compared with the equation, h = 5 and k = -4
Since the concavity is -3,
a= -3
\(y=-3(x-5)^2\text{ + (-4)}\)\(\begin{gathered} y=-3(x-5)^2\text{ -4} \\ y=-3(x^2-10x+25\text{) - 4} \\ y=-3x^2\text{ + 30x -75 -4} \\ y=-3x^2\text{ + 30x -79} \end{gathered}\)From the graph shown, it can be seen that the parabolic curve is concave down
To get the y-intercept
we will have to put x = 0 into the equation
\(\begin{gathered} y\text{ = -3(0) + 30 (0) - 79} \\ y-intercept\text{ = -79} \end{gathered}\)
find real and imaginary parts of a complex number calculator
Answers
To find the real and imaginary parts of a complex number, write it in the form a + bi, where a is the real part and b is the imaginary part.
To find the real and imaginary parts of a complex number, you can use the following steps:1. Write the complex number in the form a + bi, where a is the real part and b is the imaginary part.
2. Identify the coefficient of the imaginary unit, "i." This coefficient is the value of "b" in the complex number.
3. The real part of the complex number is given by "a," and the imaginary part is given by "b."
For example, let's consider the complex number z = 3 + 2i.The real part, denoted as Re(z), is 3, and the imaginary part, denoted as Im(z), is 2.Therefore, Re(z) = 3 and Im(z) = 2.By following these steps, you can easily determine the real and imaginary parts of any complex number.
To learn more about complex number click here
brainly.com/question/20566728
#SPJ11
What is the area of 9yd and 5yd and how’d you get it
Answers
9514 1404 393
Answer:
45 yd²
Step-by-step explanation:
The area of a rectangle is the product of its length and width. If your given measures are the length and with of a rectangle, the area is found by multiplying them.
A = LW
A = (9 yd)(5 yd) = 9·5 yd·yd = 45 yd²
The area of a 9 yd by 5 yd rectangle is 45 square yards.
Use the simplex algorithm to find the optimal solution to the following LP (solve manually): maxz= 36x1+30x2−3x3−4x4
s.t. x1+x2−x3≤5
6x1+5x2−x4≤10
∀xi≥0
Answers
The maximum value of z is 0, and the values of the decision variables are x1 = 0, x2 = 10, x3 = 0, x4 = 0.
maximize: z = c1x1 + c2x2 + ... + cnxn
subject to
a11x1 + a12x2 + ... + a1nxn ≤ b1
a21x1 + a22x2 + ... + a2nxn ≤ b2
am1x1 + am2x2 + ... + amnxn ≤ bmxi ≥ 0 for all i
In our case,
the given LP is:maximize: z = 36x1 + 30x2 - 3x3 - 4x
subject to:
x1 + x2 - x3 ≤ 5
6x1 + 5x2 - x4 ≤ 10
xi ≥ 0 for all i
We can rewrite the constraints as follows:
x1 + x2 - x3 + x5 = 5 (adding slack variable x5)
6x1 + 5x2 - x4 + x6 = 10 (adding slack variable x6)
Now, we introduce the non-negative variables x7, x8, x9, and x10 for the four decision variables:
x1 = x7
x2 = x8
x3 = x9
x4 = x10
The objective function becomes:
z = 36x7 + 30x8 - 3x9 - 4x10
Now we have the problem in standard form as:
maximize: z = 36x7 + 30x8 - 3x9 - 4x10
subject to:
x7 + x8 - x9 + x5 = 5
6x7 + 5x8 - x10 + x6 = 10
xi ≥ 0 for all i
To apply the simplex algorithm, we initialize the simplex tableau as follows:
| Cj | x5 | x6 | x7 | x8 | x9 | x10 | RHS |
---------------------------------------------------------------------------
z | 0 | 0 | 0 | 36 | 30 | -3 | -4 | 0 |
---------------------------------------------------------------------------
x5| 0 | 1 | 0 | 1 | 1 | -1 | 0 | 5 |
---------------------------------------------------------------------------
x6| 0 | 0 | 1 | 6 | 5 | 0 | -1 | 10 |
---------------------------------------------------------------------------
Now, we can proceed with the simplex algorithm to find the optimal solution. I'll perform the iterations step by step:
Iteration 1:
1. Choose the most negative coefficient in the 'z' row, which is -4.
2. Choose the pivot column as 'x10' (corresponding to the most negative coefficient).
3. Calculate the ratios (RHS / pivot column coefficient) to find the pivot row. We select the row with the smallest non-negative ratio.
Ratios: 5/0 = undefined, 10/(-4) = -2.5
4. Pivot at the intersection of the pivot row and column. Divide the pivot row by the pivot element to make the pivot element 1.
5. Perform row operations to
make all other elements in the pivot column zero.
After performing these steps, we get the updated simplex tableau:
| Cj | x5 | x6 | x7 | x8 | x9 | x10 | RHS |
---------------------------------------------------------------------------
z | 0 | 0 | 0.4 | 36 | 30 | -3 | 0 | 12 |
---------------------------------------------------------------------------
x5| 0 | 1 | -0.2 | 1 | 1 | -1 | 0 | 5 |
---------------------------------------------------------------------------
x10| 0 | 0 | 0.2 | 1.2 | 1 | 0 | 1 | 2.5 |
---------------------------------------------------------------------------
Iteration 2:
1. Choose the most negative coefficient in the 'z' row, which is -3.
2. Choose the pivot column as 'x9' (corresponding to the most negative coefficient).
3. Calculate the ratios (RHS / pivot column coefficient) to find the pivot row. We select the row with the smallest non-negative ratio.
Ratios: 12/(-3) = -4, 5/(-0.2) = -25, 2.5/0.2 = 12.5
4. Pivot at the intersection of the pivot row and column. Divide the pivot row by the pivot element to make the pivot element 1.
5. Perform row operations to make all other elements in the pivot column zero.
After performing these steps, we get the updated simplex tableau:
| Cj | x5 | x6 | x7 | x8 | x9 | x10 | RHS |
---------------------------------------------------------------------------
z | 0 | 0 | 0.8 | 34 | 30 | 0 | 4 | 0 |
---------------------------------------------------------------------------
x5| 0 | 1 | -0.4 | 0.6 | 1 | 5 | -2 | 10 |
---------------------------------------------------------------------------
x9| 0 | 0 | 1 | 6 | 5 | 0 | -5 | 12.5 |
---------------------------------------------------------------------------
Iteration 3:
No negative coefficients in the 'z' row, so the optimal solution has been reached.The optimal solution is:
z = 0
x1 = x7 = 0
x2 = x8 = 10
x3 = x9 = 0
x4 = x10 = 0
x5 = 10
x6 = 0
Therefore, the maximum value of z is 0, and the values of the decision variables are x1 = 0, x2 = 10, x3 = 0, x4 = 0.
Learn more about Simplex Algorithm here:
https://brainly.in/question/46895640
#SPJ11