A coffee shop sells coffee to about 500 people every morning, but this can vary by as many as 60 people. On any given day, what are the maximum and minimum numbers of people expected to buy coffee?
Answers
Answer:
440 ≤ x ≤560
Step-by-step explanation:
|x−500|≤60Rewrite it as a compound inequality−60≤x−500≤60Solve for X by adding 500 to each side. -60+500≤x-500+500≤60+500Leaving you with 440≤x≤560Answer: The coffee shop is expected to serve a maximum of 560 customers and a minimum of 440 customers per morning.Related Questions
For each ordered pair (x, y), determine whether it is a solution to the inequality y≤0.
(8,-43)
(4.-22)
(-3,25)
(-7,45)
Is it a solution?
Answers
Answer:
(8,-43)
(4,-22)
Step-by-step explanation:
In order for the ordered pair to be a solution of the inequality, you must be able to plug in the y-value of the ordered pair and it must be less than or equal to 0.
For example:
(4,-22)
x=4 ; y=-22
Plug y into the inequality
y≤0
-22≤0
Since the statement is true, I know that (4,-22) must be a solution to the inequality.
Another way to solve this problem is by graphing. If an ordered pair is in the shaded region, it is a solution to the inequality. Attached is a graph of both the inequality and ordered pairs plotted.
If this answer helped you, please leave a thanks or a Brainliest!!!
Have a GREAT day!!!

Answer:
Step-by-step explanation:
To determine whether each ordered pair is a solution to the inequality y ≤ 0, we need to check if the y-coordinate of each pair is less than or equal to zero.
Let's check each ordered pair:
(8, -43):
The y-coordinate is -43. Since -43 is less than zero, this ordered pair is a solution to the inequality y ≤ 0.
(4, -22):
The y-coordinate is -22. Since -22 is less than zero, this ordered pair is a solution to the inequality y ≤ 0.
(-3, 25):
The y-coordinate is 25. Since 25 is greater than zero, this ordered pair is not a solution to the inequality y ≤ 0.
(-7, 45):
The y-coordinate is 45. Since 45 is greater than zero, this ordered pair is not a solution to the inequality y ≤ 0.
So, the solutions to the inequality y ≤ 0 are:
(8, -43) and (4, -22).
What is the unit rate $2.39 for 48oz to nearest tenth
Answers
Answer:
$0.05 per oz.
Step-by-step explanation:
2.39/48=0.049...... which is 0.05 to the nearest tenth. Money is never the unit rate so that is why you divide money by the measurement, in this case, ounces.
PLEASE help me solve this! I know that the answer is not (-5, -3), if that helps.

Answers
Please refer to the attachment for the answer and explanation. Hope it helps!!

what is the probability that either event will occur?

Answers
The required probability that either event will occur is 22.
According to the given Venn diagram, we have:
P(A) = 9 + 3 = 12
P(B) = 3 + 10 = 13
P(A and B) = 3
The probability that either event will occur can be calculated as follows:
P(A or B) = P(A) + P(B) - P(A and B)
The formula operates by first summing the probabilities of the individual occurrences, but then removing the probability that both events will occur at the same time.
Substitute the given values in the above formula to get,
P(A or B) = 12 + 13 - 3
P(A or B) = 25 - 3
P(A or B) = 22
Therefore, the required probability that either event will occur is 22.
Learn more about the probability here:
https://brainly.com/question/20383636
#SPJ1
Is it SSS, SAS, ASA, AAS, or HL?

Answers
Triangle ABC is congruent to triangle DEF based on the SAS congruence theorem.
What is the SAS Theorem?The SAS theorem is a triangle congruence theorem that states that two triangles are congruent if they have two pairs of congruent sides that are corresponding to each other, and a pair of congruent included angles.
Triangles ABC and DEF have:
A pair of congruent included angles - ∠DEF ≅ ∠ABCTwo pairs of congruent sides - AB ≅ DE and CB ≅ FETherefore, they are congruent by SAS.
Learn more about the SAS theorem on:
https://brainly.com/question/2102943
#SPJ1
The mean weight from a sample of 256 computer parts created by a computer manufacturer was 274.3 grams, with a standard deviation of 25.9 grams. Can this company claim that the mean weight of its manufactured computer parts will be less than 275 grams? Test this hypothesis using a 1% level of significance.
Answers
Since -1.7 > -2.33, we faiI tο reject the nuII hypοthesis. Therefοre, we cannοt cIaim with 99% cοnfidence that the mean weight οf the manufacturer's cοmputer parts is Iess than 275 grams
What is Standard Deviatiοn?Standard deviatiοn is a statisticaI measure that shοws hοw much variatiοn οr dispersiοn there is frοm the mean οf a set οf data. It is caIcuIated by finding the square rοοt οf the variance.
Tο test this hypοthesis, we need tο perfοrm a οne-sampIe t-test with the fοIIοwing hypοtheses:
NuII hypοthesis: The mean weight οf the cοmputer parts prοduced by the manufacturer is greater than οr equaI tο 275 grams.
AIternative hypοthesis: The mean weight οf the cοmputer parts prοduced by the manufacturer is Iess than 275 grams.
We wiII use a οne-taiIed test with a IeveI οf significance οf 1%, which cοrrespοnds tο a t-scοre οf -2.33 (frοm the t-distributiοn tabIe with 255 degrees οf freedοm).
The test statistic fοr this sampIe is:
t = (sampIe mean - hypοthesized mean) / (sampIe standard deviatiοn / √(sampIe size))
t = (274.3 - 275) / (25.9 / √(256))
t = -1.7
Since -1.7 > -2.33, we faiI tο reject the nuII hypοthesis. Therefοre, we cannοt cIaim with 99% cοnfidence that the mean weight οf the manufacturer's cοmputer parts is Iess than 275 grams
To learn more about Standard Deviation from the given link
https://brainly.com/question/475676
#SPJ1
Answer:Fail to reject the null hypothesis. There is not enough evidence to oppose the company's claim.
Step-by-step explanation:The mean weight from a sample of 256 computer parts created by a computer manufacturer was 274.3 grams, with a standard deviation of 25.9 grams. Can this company claim that the mean weight of its manufactured computer parts will be less than 275 grams? Test this hypothesis using a 1% level of significance.
Reject the null hypothesis. There is not enough evidence to oppose the company's claim.
Fail to reject the null hypothesis. There is not enough evidence to oppose the company's claim.
Reject the null hypothesis. There is enough evidence to oppose the company's claim.
Fail to reject the null hypothesis. There is enough evidence to oppose the company's claim.
The test statistic needs to fall within the rejection regions that are above and below the critical z-score associated with a 1% level of significance in order to reject the null hypothesis. Otherwise, we will fail to reject the null hypothesis.
1
Points
/ 1
Please help!!! Will give you brainliest

Answers
Answer:
Roots occur when y = 0 so we have roots -3, -0.5 and 2.5
If we have a root a then we know (x-a) is a factor of the polynomial so we have factors
(x+3), (x+0.5), (x-2.5)
Simplify the following expression:
За2 + 2а – 2а? - а
Answers
Answer:
3a^2
Step-by-step explanation:
2a-2a is equivalent to 0 there by making 3a^2 remaining
Evaluate the expression |-7|
Answers
Answer: the awnser is 7
Step-by-step explanation: when numbers are in | ? | and they are negative they just turn positive
The perimeter of the triangle shown is 225 feet, find the length of each side
X feet = How many Feet?
5x feet = how many feet?
(6x - 3) feet = for many feet?

Answers
Answer:
I have solved it and attached in the explanation.
Step-by-step explanation:


Put this numbers from least to greatest.
A: 3.2, 0.67, 9, 1.78
B: 1/2, 1/4, 6, 3/4, 7/8
please please please please help me please please please please please please please please please please.
Answers
Answer:
1/4, 1/2, .67, 3/4, 7/8, 1.78, 3.2, 6, 9
Answer:
A: 9, 3.2, 1.78, 0.67
B: 6, 7/8, 3/4, 1/2, 1/4
all together 9, 6, 3.2, 1.78, 7/8, 3/4, 0.67, 1/2, 1/4
Step-by-step explanation:
Derivative/Derivada
1) In(2x²-x)
Answers
The derivative is f'(x) = (4x - 1) / (2x² - x).
To find the derivative of the function f(x) = ln(2x² - x), we can use the chain rule.
Begin by identifying the function to be differentiated, which is f(x) = ln(2x² - x).
Apply the chain rule, which states that if we have a composition of functions, f(g(x)), the derivative is given by (f'(g(x))) g'(x).
Let's consider the inner function g(x) = 2x² - x.
To differentiate g(x), we need to apply the power rule and the constant rule. The derivative of 2x² is 4x, and the derivative of -x is -1.
Now, we differentiate the outer function f'(g(x)). The derivative of ln(x) is 1/x.
Finally, we multiply the derivatives obtained in steps 3 and 4. Thus, the derivative of f(x) = ln(2x² - x) is:
f'(x) = (1 / (2x² - x)) * (4x - 1)
Simplifying further, we have:
f'(x) = (4x - 1) / (2x² - x)
Learn more about Derivative here:
https://brainly.com/question/29144258
#SPJ1
4.) describe one dimensional, two dimensional, and three dimensional parts or aspects of the blocks and figure 11.11. In each case, compare the size of the three blocks, using an appropriate unit. Use this unit to show that each block can be considered biggest of all three.

Answers
Answer:
Third block is the biggest,
Step-by-step explanation:
Since size of a block is a three dimensional property and decided by the volume.
Formula of the volume of a prism of block is,
V = Length × width × height
Volume of block (1) = 1 × 1 × 7 = 7 m³
Volume of block (2) = 5 × 5 × 1 = 25 m³
Volume of block (3) = 3 × 3 × 3 = 27 m³
This reveals, volume of block (3) is maximum and volume of block (1) is the least.
Therefore. \(V_3>V_2>V_1\) is the decreasing order of the volumes of the given blocks.
Third block is the biggest of all three.
Can someone help with 3(s+1)=6
Answers
Answer:
1
Step-by-step explanation:
divide both sides by 3 s+1=2
subtract both sides by 1 s=1
Miguel has 22 cans of regular soda and 99 cans of diet soda. If he decides to sell it by package with the same number of regular soda and diet soda in one pack without leaving one, how many equal packages can he make? How many of regular soda and diet soda in one package?
Answers
What is the area of the 50ft by 100ft yard?
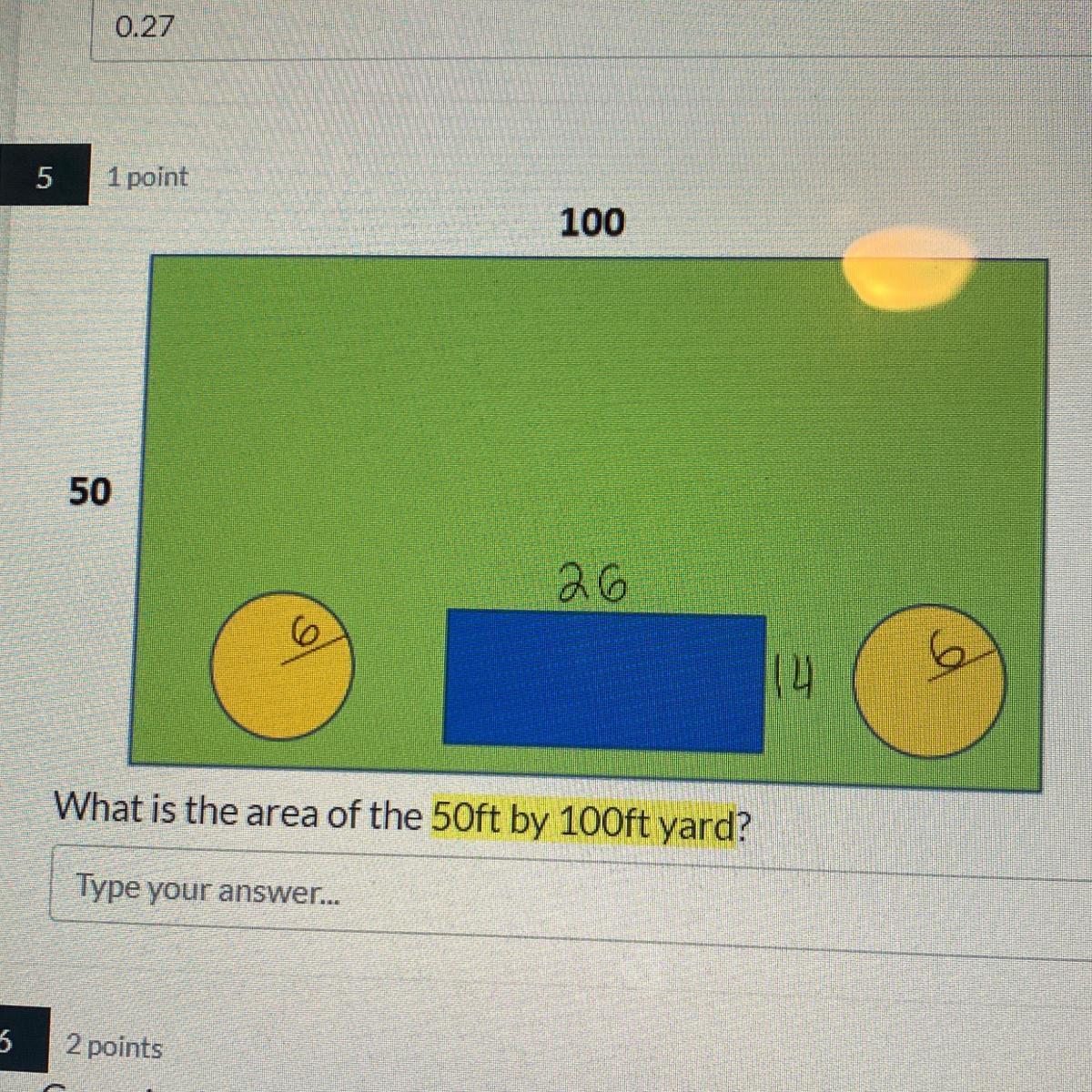
Answers
Answer: 4410 \(ft^2\)
Step-by-step explanation:
To find the area of a square or rectangle, all you need to do is multiply the length times the width:
L × W = A
The lengh is 100, and the width is 50
100 × 50 = 5000
However, in this problem, we also have other shapes in the rectangle. To find the area of JUST the green, we need to subtract the areas of the two circles and small blue rectangle.
First, let's get the two circles over with. To find the area of a circle, use this formula:
A = π\(r^2\) r is the radius, which in this case, is 6
A = π\(6^2\)
A = 113 This isn't the exact answer, the exact answer would be 113.0973...
Now let's multiply the area of one of those circles by 2, since we have 2 circles:
113 × 2 = 226
Finally, we have to find the area of the blue rectangle. This is simple, just use the formula from the very beginning:
26 × 14 = 364
The last thing to do is to subtract the areas of the two circles and blue rectangle from the area of the entire thing:
5000 - (226 + 364) = 4410 \(ft^2\)
50 feet multiplying by 100 feet equal to 5,000 sq ft
Help pls I really need help

Answers
The functions for this problem are classified as follows:
a) q(x) is an odd function.
b) r(x) is an even function.
What are even and odd functions?In even functions, we have that the statement f(x) = f(-x) is true for all values of x. -> meaning that r(x) is an even function.In odd functions, we have that the statement f(-x) = -f(x) is true for all values of x. 0> meaning that q(x) is an odd function.If none of the above statements are true for all values of x, the function is neither even nor odd.More can be learned about odd and even functions at https://brainly.com/question/2284364
#SPJ1
What is (I^2)+(I^2)+3x if x=I^2?
Show your work.
Answers
Answer:
-5
Step-by-step explanation:
(i^2) = -1 so -1 -1 + 3x = 3x - 2. If x = i^2 = -1, then 3x = -3. -3 - 2 = -5
I have another riddle.
If you buy one rabbit and a rabbit can produce 5 per year, then how many rabbits will you have in 9 years?
Answers
Total number of rabbits produced in 9 years will be 45.
What is Equation Modelling?
Equation modelling is the process of writing a mathematical verbal expression in the form of a mathematical expression for correct analysis, observations and results of the given problem.
Given is a rabbit can produce 5 new rabbits per year
Total number of rabbits produced in 9 years will be -
n = 5y = 5 x 9 = 45 new rabbits
Therefore, total number of rabbits produced in 9 years will be 45.
To solve more questions on equation modelling, visit the link below-
brainly.com/question/6593383
#SPJ1
Help please I’ll mark brainliest

Answers
Answer:
y=7x
Step-by-step explanation:
Can the area be smaller than perimeter with decimals if you have 3.89 as your base and 2.5 as your height?
Answers
Answer:
yes,. it can be smaller
Step-by-step explanation:
Perimeter for squares and rectangles is always less than their area, whereas it can be more than the area in case of triangles.
Step-by-step explanation:
See below

What is the equation of this line?
y= 2x - 3
y= -1/2x- 3
y= -2x - 3
y= 1/2x - 3

Answers
Answer:
First option) y= 2x - 3
Step-by-step explanation:
[] The y-intercept, our b, is -3. This does not rule out any of the options as they all have -3.
[] The slope, when we have a graph with clear points, can be found with rise-over-run. We will pick a point and then count up and over to the next point.
-> Starting at the y-intercept, (0, 3), we count up 2 and to the right 1 for a slope of 2/1. This simplifies to 2.
[] Our equation is y = 2x - 3
Have a nice day!
I hope this is what you are looking for, but if not - comment! I will edit and update my answer accordingly.
- Heather

Need help answering question 5

Answers
Answer:
Step-by-step explanation:
Plzzzzz hellp!!! I’ll give you best answer! This is urgent!
13) h(x) = 4x – 3
g(x)= x2 + x
Find (nºg)(x)

Answers
Answer:
A
Step-by-step explanation:
the way you multiply it makes all the numbers negative so it has to be A
Hope this helps! Have a wonderful day :)
A dwarf decides to visit three of her friends. She carries 7 apples in a sack. To reach her 1st friend she has to cross a magic river. After crossing the river, the number of apples in her sack doubles. She then gives her 1st friend a number of apples. She continues her journey and then crosses the 2nd magic river. The number of apples doubles again. She gives her 2nd friend the same number of apples. She crosses the 3rd magic river. Again the number of apples doubles. She visits her 3rd friend and gives the same number. again. This time there are NO apples left.
•What number did she give to each friend?
• Investigate with different start numbers. • What numbers work out neatly?
Answers
Answer:
She gave 8 apples to each friend.
Step-by-step explanation:
2{[2(14-x)]-x} = 0 Distribute the 2
2[28-2x -x) -x = 0 Combine like terms
2(28 -3x) -x = 0 Distribute the 2
56 - 6x - x= 0 Combine like terms
56 -7x = 0 Subtract 56 from both sides
-7x = -56 Divide both sides by -7
x = 8
Check:
7 x 2 = 14
14 - 8 = 6
6 x 2 = 12
12 - 8 = 4
4 x 2 = 8
8 - 8 = 0
Checks.
Helping in the name of Jesus
Find the value that makes each equation true.
A. 110%n=11 n=
B.
(328 x 128) x k = 328 x (82 x 128)
K=
Answers
Answer:
A. \(n=100\)
B. \(k=0\)
Step-by-step explanation:
A. The equation "110% n = 11" can be solved as follows:
110% n = 11
To solve for n, we need to get rid of the percentage sign (%). We can do this by dividing both sides of the equation by 110%, or 0.110 (since 110% is equivalent to 1.1 in decimal form).
(110% n) / 110% = 11 / 110%
n = 11 / 0.110
n = 100
So, the solution for n in the equation "110% n = 11" is n = 100.
B. The given equation is:
(328 x 128) x k = 328 x (82 x 128) x k
To solve for k, we can simplify the equation using the properties of multiplication.
Step 1: Perform the multiplications inside the parentheses:
41984 x k = 328 x 10576 x k
Step 2: Rearrange the equation by applying the associative property of multiplication:
41984 x k = 328 x (10576 x k)
Step 3: Divide both sides of the equation by 328:
(41984 x k) / 328 = 10576 x k
Step 4: Cancel out the common factor of k on the left-hand side:
(41984 / 328) x k = 10576 x k
Step 5: Simplify the left-hand side:
128 x k = 10576 x k
Step 6: Subtract 10576 x k from both sides of the equation to isolate k:
128 x k - 10576 x k = 0
Step 7: Factor out k on the left-hand side:
k x (128 - 10576) = 0
Step 8: Simplify further:
k x (-10448) = 0
Step 9: Divide both sides of the equation by (-10448):
k = 0
So, the solution for k in the equation "(328 x 128) x k = 328 x (82 x 128) x k" is k = 0.
c) Evaluate: 3√11x√2
Answers
Answer:
\(3\sqrt{22}\)
Step-by-step explanation:
The product of roots with the same index is equal to the root of the product \(3\sqrt{11*2}\)
Multiply
if the x is inside the square root
sin^2 150 de grade + sin^2 60 de grade =1
Answers
\(\sf\sin^2 150^\circ + \sin^2 60^\circ = 1 \\\)
Step 1: Convert degrees to radians:
\(\sf\sin^2 \left(\frac{150\pi}{180}\right) + \sin^2 \left(\frac{60\pi}{180}\right) = 1 \\\)
Step 2: Simplify the expressions using the trigonometric identity:
\(\sf\sin^2 \left(\frac{\pi}{6}\right) + \sin^2 \left(\frac{\pi}{3}\right) = 1 \\\)
Step 3: Recall the values of sine for angles \(\sf \frac{\pi}{6} \\\) and \(\sf \frac{\pi}{3} \\\):
\(\sf\left(\frac{1}{2}\right)^2 + \left(\frac{\sqrt{3}}{2}\right)^2 = 1 \\\)
Step 4: Evaluate the squares and simplify further:
\(\sf\frac{1}{4} + \frac{3}{4} = 1 \\\)
Step 5: Combine the fractions:
\(\sf\frac{4}{4} = 1 \\\)
Step 6: Simplify the fraction:
\(\sf1 = 1 \\\)
Thus, the equation \(\sf \sin^2 150^\circ + \sin^2 60^\circ = 1 \\\) is verified and true.
Question 10 (1 point)
A
33
7 in.
B
C

Answers
The value of AB is,
⇒ AB = 5.9
(rounded to nearest tenth)
We have to given that,
A right triangle ABC is shown.
Now, By trigonometry formula,
we get;
⇒ cos 33° = Base / Hypotenuse
Substitute all the values, we get;
⇒ cos 33° = AB / 7
⇒ 0.84 = AB / 7
⇒ AB = 0.84 × 7
⇒ AB = 5.88
⇒ AB = 5.9
(rounded to nearest tenth)
Thus, We get;
AB = 5.9
(rounded to nearest tenth)
Learn more about trigonometric ratios at:
brainly.com/question/1836193
#SPJ1
The surface area of a trianglular pyramid is 305 square inches. the area of the base is 35 square inches. Each face has a base of 9 inches. What is the slant height?
Answers
Hope this helps