13. How much money will 8820 Vield in investa
+ 5%. for 3 years and compounded
continuosly and semiannually and determine
which eams more?
Answers
9514 1404 393
Answer:
10,247.38 from continuous compounding10,228.50 from semiannual compoundingcontinuous compounding earns moreStep-by-step explanation:
The formula for the account balance from continuously compounded interest at annual rate r for t years is ...
A = Pe^(rt) . . . . P = principal invested
A = 8820e^(0.05·3) ≈ 10,247.38 . . . continuous compounding
__
The formula for the account balance from interest compounded semiannually at annual rate r for t years is ...
A = P(1 +r/2)^(2t)
A = 8820(1 +.05/2)^(2·3) ≈ 10,228.50 . . . semiannual compounding
Continuous compounding earns more.
Related Questions
1 8 The scale blueprint of a rectangular pool is drawn inch - 1 foot. If the pool is 34 feet long, what is the measure of the pool's length on the blueprint? A) 3.5 in B) 3.75 in C) 4.25 in D) 4.5 in E) 4.75 in
Answers
Answer:
C
Step-by-step explanation:
The scale blueprint of a rectangular pool is drawn 1/8 in - 1 foot. If the pool is 34 feet long, what is the measure of the pool's length on the blueprint
A scale drawing is a reduced form in terms of dimensions of an original image / building / object
the scale drawing is usually reduced at a constant dimension
scale of the drawing = original dimensions / dimensions of the scale drawing
Blueprint's length = 34 x 1/8 = 4.25
i need help this is due tomorrow

Answers
a. Equation: (1/2)/4, Answer: 1/8
b) Equation: (1 1/2)/(1/4), Answer: 6
c) Equation: 10(1/4+1/8), Answer: 3 3/4
Fill in the missing values below one at a time to find the quotient when x^3 - x^2 - 3x + 2 is divided by x - 2.

Answers
Therefore, the quotient when x³ - x² - 3x + 2 is divided by x - 2 is x² - 2x - 5 with a remainder of -3.
To find the quotient when x³ - x² - 3x + 2 is divided by x - 2, we will use the long division method. Here is the solution:
Step 1: The first term of the quotient is x². Multiply x² by x - 2 to get x³ - 2x². Subtract this product from x³ - x² to get: x² - 3x² = -2x²
Step 2: Bring down the next term of the dividend, which is -3x. The new dividend is -2x² - 3x.
Step 3: The second term of the quotient is -2x. Multiply -2x by x - 2 to get -2x² + 4x. Subtract this product from -2x² - 3x to get -5x.
Step 4: Bring down the last term of the dividend, which is +2. The new dividend is -5x + 2. Step 5: The third term of the quotient is -5. Multiply -5 by x - 2 to get -5x + 10. Subtract this product from -5x + 2 to get -3.
For such more question on Multiply
https://brainly.com/question/29793687
#SPJ8
The sample standard deviation of a set of numbers is calculated below. Fill in the blank for the missing part of this calculation.

Answers
The table given shows the calculation of the variance and standard deviation of a given sample.
The formula for the variance is given as shown below;
\(\begin{gathered} S^2=\frac{\Sigma(x_i-\mu)^2}{n-1} \\ \text{Where;} \\ S^2=S\tan dard\text{ deviation} \\ \Sigma=Summation(addition) \\ x_i=value\text{ from observed data} \\ \mu=\operatorname{mean}\text{ from the observed data} \\ n=\text{sample size} \end{gathered}\)When we substitute for the values given, this becomes;
\(\begin{gathered} S^2=\frac{\Sigma(x_i-\mu)^2}{6-1} \\ S^2=\frac{361+196+4+36+9+16}{5} \\ S^2=\frac{622}{5} \\ S^2=124.4 \end{gathered}\)Therefore, the missing value is 622.
This is the addition of each observed data minus the mean (that is, the addition of the third column).
The sum of two integers is 44. The difference of the two integers is 8.
What is the smaller integer?
Answers
Answer:
18
Step-by-step explanation:
44/2=22
the difference between the two numbers= 8
8/2=4
(22-4) + (22+4) = 18+26 = 44
the smaller number = 18
Answer:
The smaller integer is 18.
Step-by-step explanation:
x is the larger integer, and y is the smaller integer.
x + y = 44
x - y = 8
For x - y = 8, add y to both sides and get x = 8 + y.
Change x in x + y = 44 for 8 + y.
8 + y + y = 44
8 + 2y = 44
2y = 36
y = 18
Figure ABCD is a parallelogram
A
B
D
C
Which transformations will carry figure ABCD onto itself?
Select all that apply.
A
A 180° rotation about the midpoint of AB.
B. A 360° rotation about the midpoint of AB.
C.
A reflection about the line joining the midpoints of AB and DC
D. A reflection about the diagonal AC
E A 180° rotation about the intersection of the two diagonals of ABCD
Answers
Answer:
A. A 180 degree rotation about the midpoints of AB.
Step-by-step explanation:
The rotation of a shape less than 360 degrees will carry the figure onto itself. A parallelogram is a rectangular shape which is slight diagonal shaped. The parallelogram will carry transformation when its rotation is about 180 degrees.
A car producer stocks three types of tires: A, B, and C. Let P(A) = 0.40, P(B) = 0.15 and P(C) = 0.45. The percentage of defective tires is 2%, 1% and 5%, respectively.
Someone picks a tire off the shelf at random and it is Brand A.
If you want to know the probability that it is a defective tire (event D), which formula would you use? If you want to know the probability that it is a defective tire (event D), which formula would you use?
a) P(AD)= PD AP(A) PD)
b) P(D|A) = P(A|DP(D) P(A)
c) P(AD)= PD APD) P(A)
d) P(DA)= P(ADP(A) PD)
Answers
Answer:
The correct option is b) \(P(D|A)=P(A|D)P(D)\).
Step-by-step explanation:
The probability of selecting the different types of tires are:
P (A) = 0.40
P (B) = 0.15
P (C) = 0.45
The defective rate for the different types of tires are:
P (D|A) = 0.02
P (D|B) = 0.01
P (D|C) = 0.05
The formula to compute the probability that the tire is defective given that it is Brand A tire as follows:
\(P(D|A)=P(A|D)P(D)\)
The slope of the line below is 3. Write the point-slope equation for the line
using the coordinates of the labeled point. (6’8)

Answers
Answer:
y - 8 = 3(x - 6)
Step-by-step explanation:
Point slope-equation formula:
y - y1 = m(x - x1)
y - 8 = 3(x - 6)
3. okkkokok final
A fully loaded and fueled spacecraft can weigh close to 3.9
million pounds. What is this weight converted to tons?
Answers
Answer:1950 US tons
Step-by-step explanation:
Rob can complete his bus route in 4 hours. Joan can complete her bus route in 3 hours. If they both left the terminal at 3:00 am and after each completed route returned to the terminal, determine the next time they would leave the terminal at the same time.
Answers
Answer:
3:00 pm
Step-by-step explanation:
Given
\(Rob = 4\ hrs\)
\(Joan = 3\ hrs\)
\(Start\ Time = 3:00\ am\)
Required
The next time they leave at the same time
To do this, we first list out the multiples of 4 and 3 (i.e. their time of completing each route)
So, we have:
\(Rob: 4, 8, 12, 16, 20...\)
\(Joan: 3,6,9,12,15,18....\)
The least common multiple in the above is:
\(Least = 12hrs\)
This means that they will meet at the terminal after 12 hours
So, their meeting time is:
\(Time = 3:00am + 12\ hrs\)
\(Time = 3:00\ pm\)
This is very urgent please tell me if the one that is highlighted all blue is correct or not left or right question,which is correct?

Answers
Answer:
right option
Step-by-step explanation:
You are given that z > 2. Write an inequality for each expression.
a) 2z+ 9
b) 3(z - 4)
c) 4+2z
d) 5(3z-2)
Answers
a) The inequality for the expression 2z + 9 is 2z + 9 > 13.
b) The inequality for the expression 3(z - 4) is 3z - 12 > -6.
c) The inequality for the expression 4 + 2z is 4 + 2z > 8.
d) The inequality for the expression 5(3z - 2) is 15z - 10 > 20.
a) To write an inequality for the expression 2z + 9, we can multiply the given inequality z > 2 by 2 and then add 9 to both sides of the inequality:
2z > 2 * 2
2z > 4
Adding 9 to both sides:
2z + 9 > 4 + 9
2z + 9 > 13
Therefore, the inequality for the expression 2z + 9 is 2z + 9 > 13.
b) For the expression 3(z - 4), we can distribute the 3 inside the parentheses:
3z - 3 * 4
3z - 12
Since we are given that z > 2, we can substitute z > 2 into the expression:
3z - 12 > 3 * 2 - 12
3z - 12 > 6 - 12
3z - 12 > -6
Therefore, the inequality for the expression 3(z - 4) is 3z - 12 > -6.
c) The expression 4 + 2z does not change with the given inequality z > 2. We can simply rewrite the expression:
4 + 2z > 4 + 2 * 2
4 + 2z > 4 + 4
4 + 2z > 8
Therefore, the inequality for the expression 4 + 2z is 4 + 2z > 8.
d) Similar to the previous expressions, we can distribute the 5 in the expression 5(3z - 2):
5 * 3z - 5 * 2
15z - 10
Considering the given inequality z > 2, we can substitute z > 2 into the expression:
15z - 10 > 15 * 2 - 10
15z - 10 > 30 - 10
15z - 10 > 20
Therefore, the inequality for the expression 5(3z - 2) is 15z - 10 > 20.
for such more question on inequality
https://brainly.com/question/17448505
#SPJ8
There are 6 acts in a talent show.
An acrobat, a dancer, a guitarist, a singer, a violinist, and a whistler.
A talent show host randomly schedules the 6 acts.
Compute the probability of each of the following events.
Event A: The acrobat is first, the singer is second, the violinist is third, and the whistler is fourth.
Event B: The first four acts are the whistler, the acrobat, the guitarist, and the dancer, In any order.
Write your answers as fractions in simplest form.
P(A) =
P (B) =
Answers
The probability of Event A is 1/360 and the probability of Event B is 1/15.
For Event A, we can calculate the probability by considering the order in which the acts are scheduled.
There are 6 acts, so there are 6 possible choices for the first act. After the first act is scheduled, there are 5 remaining acts, so there are 5 possible choices for the second act.
Similarly, there are 4 possible choices for the third act, and 3 possible choices for the fourth act.
Finally, there are 2 possible choices for the fifth act, and only 1 choice remains for the last act.
Therefore, the total number of possible ways to schedule all 6 acts is:
6 x 5 x 4 x 3 x 2 x 1 = 720
Since we are only interested in one specific order of the first four acts, we need to count the number of ways to schedule the remaining two acts after the first four have been scheduled in the desired order.
There are 2 remaining acts, so there are 2 possible choices for the fifth act.
Only one act remains for the last slot.
Therefore, the total number of ways to schedule all 6 acts such that the acrobat is first, the singer is second, the violinist is third, and the whistler is fourth is:
1 x 1 x 1 x 1 x 2 x 1 = 2
Thus, the probability of Event A is:
P(A) = 2/720 = 1/360
For Event B, we want to count the number of ways to schedule the first four acts as the whistler, the acrobat, the guitarist, and the dancer, in any order.
There are 4 acts, so there are 4 possible choices for the first act. After the first act is scheduled, there are 3 remaining acts, so there are 3 possible choices for the second act.
Similarly, there are 2 possible choices for the third act, and only one choice remains for the fourth act.
Therefore, the total number of possible ways to schedule the first four acts is:
4 x 3 x 2 x 1 = 24
Since we do not care about the order in which the last two acts are scheduled, we can simply choose any two acts from the remaining 2. There are 2 ways to do this.
Therefore, the total number of ways to schedule all 6 acts such that the first four acts are the whistler, the acrobat, the guitarist, and the dancer, in any order is:
24 x 2 = 48
Thus, the probability of Event B is:
P(B) = 48/720 = 1/15
To learn more about the probability;
brainly.com/question/11234923
#SPJ1
8) A car wash had to make their soap last 9 days. If they only have one-ninth of a gallon of soap, how much should they use each day so it lasts 9 days?
Answers
Answer:
9/81
Step-by-step explanation:
Because 1/9 is all they have so they need to reduce usage by nine so divide by nine It probably wrong tho srry :(
Answer:
2/81
Step-by-step explanation:
it says that 1/9 gallon has to be used over 9 days, so you would divide 1/9 by 9, which is basically multiplying 1/9 and 1/9, because you flip the second fraction around when dividing. 1/9 x 1/9 is 2/81, and it is already in simplest form, therefore the answer is 2/81 of a gallon. hope this helped
expand and simplify 2 (x+7) +3 (x+1)
Answers
2(x + 7) + 3(x + 1) =
= 2x + 14 + 3x + 3 = 5x + 17
5.- 6x + y = 66x + 3y =- 12
Answers
We are going to use the Elimination Method.
This is: we are going to add both sides of the equations so our result is an equation with just one variable.
Step 1We have that if we add the equations, we will eliminate the x term, then we go ahead:
- 6x + y = 6
6x + 3y =- 12
____________
0x + 4y = -6
because -6x + 6x = 0x, y + 3y = 4y and 6 - 12 = -6
Step 2Now, we have an equation for y
0x + 4y = -6
↓
4y = -6
Taking 4 to the right side of the equation:
4y = -6
↓
y = -6/4 = -1.5
Then y = -1.5
Step 3Now we find x by replacing y = -1.5 in any of the given equations:
-6x + y = 6
↓
-6x - 1.5 = 6
Taking -1.5 and -6 to the right side of the equation:
-6x - 1.5 = 6
↓ taking -1.5
-6x = 6 + 1.5 = 7.5
-6x = 7.5
↓ taking -6
x = 7.5/(-6) = -1.25
Then x = -1.25
Answer- the solution of the system is x = -1.25 and y = -1.5: (-1.25, -1.5)
A manufacturer must test that his bolts are 4.00 cm long when they come off the assembly line. He must recalibrate his machines if the bolts are too long or too short. After sampling 121 randomly selected bolts off the assembly line, he calculates the sample mean to be 4.21 cm. He knows that the population standard deviation is 0.83 cm. Assuming a level of significance of 0.02, is there sufficient evidence to show that the manufacturer needs to recalibrate the machines? Step 2 of 3: Compute the value of the test statistic. Round your answer to two decimal places.
Answers
The sample mean of 4.21 cm is significantly different from the specified target mean of 4.00 cm.
Step 1: State the hypotheses.
- Null Hypothesis (H₀): The mean length of the bolts is 4.00 cm (μ = 4.00).
- Alternative Hypothesis (H₁): The mean length of the bolts is not equal to 4.00 cm (μ ≠ 4.00).
Step 2: Compute the value of the test statistic.
To compute the test statistic, we will use the z-test since the population standard deviation (σ) is known, and the sample size (n) is large (n = 121).
The formula for the z-test statistic is:
z = (X- μ) / (σ / √n)
Where:
X is the sample mean (4.21 cm),
μ is the population mean (4.00 cm),
σ is the population standard deviation (0.83 cm), and
n is the sample size (121).
Plugging in the values, we get:
z = (4.21 - 4.00) / (0.83 / √121)
z = 0.21 / (0.83 / 11)
z = 0.21 / 0.0753
z ≈ 2.79 (rounded to two decimal places)
Step 3: Determine the critical value and make a decision.
With a level of significance of 0.02, we perform a two-tailed test. Since we want to determine if the mean length of the bolts is different from 4.00 cm, we will reject the null hypothesis if the test statistic falls in either tail beyond the critical values.
For a significance level of 0.02, the critical value is approximately ±2.58 (obtained from the z-table).
Since the calculated test statistic (2.79) is greater than the critical value (2.58), we reject the null hypothesis.
Conclusion:
Based on the computed test statistic, there is sufficient evidence to show that the manufacturer needs to recalibrate the machines. The sample mean of 4.21 cm is significantly different from the specified target mean of 4.00 cm, indicating that the machine's output is not meeting the desired length. The manufacturer should take action to recalibrate the machines to ensure the bolts meet the required length of 4.00 cm.
for more such question on mean visit
https://brainly.com/question/1136789
#SPJ8
3x-30=0
why does it equal 0 and how would I solve for it
Answers
Answer: the reason why 3x - 30 = 0 is because x = 10
Step-by-step explanation:
3x - 30 = 0
first we try to get the value of x
so
3x = 30
x = 30/3
x = 10
so the reason why 3x - 30 = 0 is because x = 10
to confirm this
we substitute the value of x=10 into the equation
3x - 30 = 0
3*10 - 30 = 0
30 - 30 = 0
Suppose you start with one liter of vinegar and repeatedly remove 0.14 L, replace with water, mix, and repeat. a. Find a formula for the concentration after n steps. b. After how many steps does the mixture contain less than 9% vinegar?
Answers
Formula for the concentration after n steps is \(C(n) = C(0) * (0.86)^n\) and
after 11 steps, the mixture contains less than 9% vinegar.
What is concentration?
Concentration in science refers to the amount of a particular substance (the solute) that is dissolved in a given amount of a solution. It is typically expressed in units of moles per liter (M or mol/L) or as a percentage or fraction of the total solution.
a. Let C(n) be the concentration of vinegar after n steps. At each step, we remove 0.14 L of the mixture, which contains C(n) liters of vinegar. So we are left with (1 - C(n)) liters of water. We then add back 0.14 L of water, giving us a total volume of 1 liter. Therefore, the concentration after one step is:
\(C(1) = C(0) * \frac{1 - 0.14}{1}\)
where C(0) is the initial concentration of vinegar, which is 1 liter per liter or 100%. After two steps, we repeat the process:
C(2) = C(1) * \(\frac{1 - 0.14}{1}\)
Substituting the formula for C(1), we get:
C(2) = C(0) * \((\frac{1 - 0.14}{1}) * (\frac{1 - 0.14}{1})\)
or, more generally:
\(C(n) = C(0) * (0.86)^n\)
b. We want to find the smallest integer n such that C(n) < 0.09 or 9%. Substituting the formula from part (a), we get:
\(C(0) * (0.86)^n < 0.09\)
Dividing both sides by C(0), we get:
\((0.86)^n < 0.09\)
Taking the natural logarithm of both sides, we get:
n * ln(0.86) < ln(0.09)
Dividing both sides by ln(0.86), we get:
n > ln(0.09) / ln(0.86)
Using a calculator, we get:
n > 10.7
Since n must be an integer, the smallest possible value of n is 11. Therefore, after 11 steps, the mixture contains less than 9% vinegar.
To learn more about concentration visit the link:
https://brainly.com/question/17206790
#SPJ1
Jordan and Taylor are collecting canned foods for the homeless. They hope to collect 10 cans per day to reach their goal. They have already collected 120 cans. If the
function for this problem is f(c) = 10r+120, determine how many cans Jordan and Taylor will have collected after 8 days.
Answers
Answer:
200 cans.
Step-by-step explanation:
f(c)=10r + 120
Put t=8 into it
T(c) = 10 x 8 + 120
=200 cans
(Use substitution method)
Two more than 5 times a number,n, is greater than 3.
Answers
Answer:
5n + 2 > 3 (If you're writing the equation)
n > 1/5 (If you're solving for n.
Step-by-step explanation:
Answer: n > 1/5
Step-by-step explanation:
2 + 5n > 3
5n > 1
n > 1/5
The answer choices are:
A. 4
B. 2 radical 5
C. 4 radical 2
D. 2 radical 10
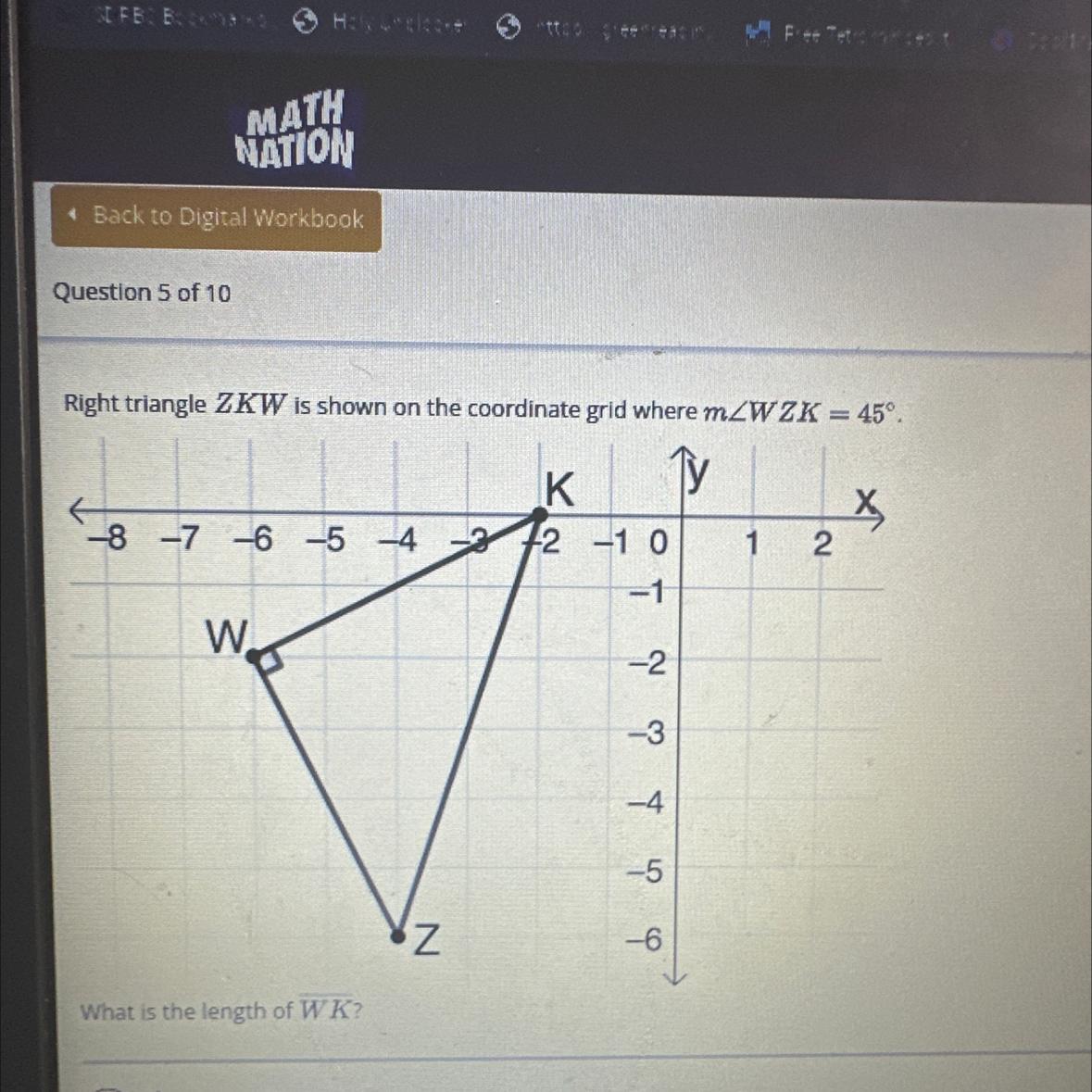
Answers
The length of segment WK is given as follows:
B. \(2\sqrt{5}\)
How to calculate the distance between two points?Suppose that we have two points of the coordinate plane, and the ordered pairs have coordinates \((x_1,y_1)\) and \((x_2,y_2)\).
The shortest distance between them is given by the equation presented as follows, derived from the Pythagorean Theorem:
\(D = \sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\)
The endpoints of the segment in this problem are given as follows:
K(-2,0) and W(-6,-2).
Hence the length of the segment is given as follows:
\(\sqrt{(2 - (-6))^2 + (0 - (-2))^2} = \sqrt{20} = \sqrt{4 \times 5} = 2\sqrt{5}\)
Meaning that option B is the correct option in the context of this problem.
More can be learned about the distance between two points at https://brainly.com/question/7243416
#SPJ1
HELP ASAP Four times the quotient of 3 and 4.

Answers
Answer:
it is 4
Step-by-step explanation:
all you do is multipla
Please help solve this for me

Answers
Answer:
i believe the answer would be option D
Step-by-step explanation:
What is the unit rate of the number of miles driven per number of hours of driving?
Answers
Answer:
MPH
Step-by-step explanation:
Four friends are attending a concert. One ticket to the concert is $75. The cost of parking is
split among the four friends If p represents the cost of parking, which equation represents the cost of 1 friend attending
the concert?

Answers
Answer:
Step-by-step explanation:
The answer is C. Sorry I can not explain why I am not good at explaining things so I you want details ask somwone else but it is for shure C.
Solve for r 1+3r>10 please I need this solved aspap
Answers
The solution to the inequality 1 + 3r > 10 is r > 3.
This means that any value of r greater than 3 will satisfy the inequality.
To solve the inequality 1 + 3r > 10, we need to isolate the variable r on one side of the inequality sign.
Let's begin by subtracting 1 from both sides of the inequality:
1 + 3r - 1 > 10 - 1
This simplifies to:
3r > 9
Next, we can divide both sides of the inequality by 3 to solve for r:
(3r)/3 > 9/3
This simplifies to:
r > 3
For similar question on inequality.
https://brainly.com/question/30604125
#SPJ8
I need help with number 7.

Answers
Answer:
A) 41%
Step-by-step explanation:
the complement of at least one balloon being hit is no balloons being hit
thus, if "at least one balloon is hit" is false, "no balloons are hit" is true
1 - probability something is false = probability it is true
1 - probability no balloons are hit = probability at least one balloon is hit
probability no balloons are hit = P(A and B and C and D and E), where each event is a balloon is not hit
probability a balloon is hit = 1/10 = 0.1
probability a ballon is not hit = 1 - probability a balloon is hit = 1-0.1 = 0.9
P(A and B) = P(A) * P(B)
P(A and B and C and D and E) = 0.9*0.9*0.9*0.9*0.9 = 0.9^5 = 0.59049 = probability no balloons are hit
1 - probability no balloons are hit = probability at least one balloon is hit = 1-0.59049 = 0.40951 ≈41%
A group of cyclists recorded the distance they have traveled.
Draw a line plot and answer the questions below.
Name
Gina
Rey
Faye
Mark
John
James
Albert
William
Nathan
Kate
Mary
Risa
Paul
Abi
Joan
Distance in
miles
40 1/2
50
35 3/4
60
45
55 1/4
60
45
40 1/2
50
45
40 1/2
60
40 1/2
35 3/4
Title:
1. How many cyclists were there?
2. What was the longest distance traveled?
3. How many cyclists traveled less than 50 miles?
4. What was the most common distance traveled by
the cyclists?
5. How many more cyclists traveled 45 miles than
55 1/4 miles?
6. How many cyclists traveled more than 45 miles
Answers
A total of 7 Cyclists traveled more than 45 miles. 4 cyclists traveled 50 miles or more, and 3 cyclists traveled more than 54 1/4 miles.
A line plot is drawn with the cyclists' names plotted on the x-axis and their corresponding distances covered plotted on the y-axis.
The dots are then joined to form a line, revealing the relationship between the cyclist's names and their corresponding distance traveled. The cyclist names and their corresponding distances are given in the table below.
Name Distance (in miles) Gina 40 1/2 Rey 50 Faye 35 3/4 Mark 60 John 45 1/2 James 40 1/2 Albert 40 1/4 William 54 1/4 Nathan 40 Kate 40 1/4 Mary 60 Risa 40 Abi 35 3/4 Joan 50 1/2 1. The number of cyclists is 14. 2. The longest distance covered by a cyclist is 60 miles.
Mary and Mark both covered this distance.3. A total of 7 cyclists traveled less than 50 miles. 4. The most common distance traveled by cyclists is 40 1/2 miles. Gina, James, and Albert covered this distance. 5. 2 more cyclists traveled 45 miles than 55 1/4 miles. Only William traveled 55 1/4 miles, while John and James both traveled 45 1/2 miles.6.
A total of 7 cyclists traveled more than 45 miles. 4 cyclists traveled 50 miles or more, and 3 cyclists traveled more than 54 1/4 miles.
For more questions on Cyclists .
https://brainly.com/question/3807925
#SPJ8
PLEASE HELP ITS URGENT I HAVE 3 MINS AND IM FAILING I REALLY NEED A A ASAP PLEASE HELP
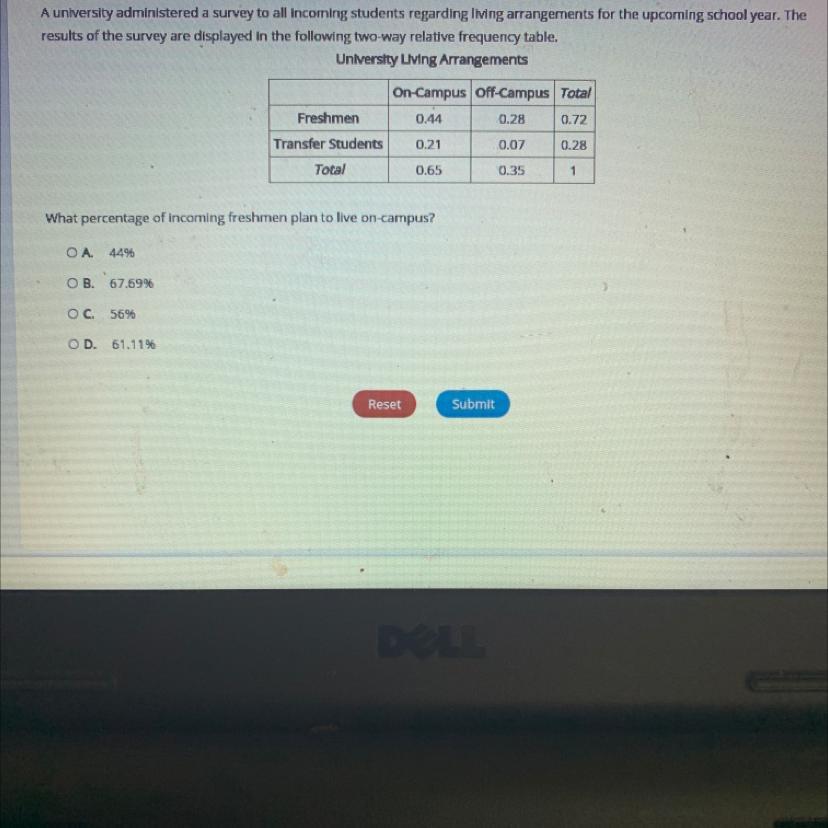
Answers
Answer:
Here to save the day Incoming freshman = 0.72 Freshman & on campus = 0.44So 44% or AAnswer:
A) 44%
Step-by-step explanation: