1. 7.35 x 10 6 – 9.42 x 10 8
2. 3.14 x 10 -3+1.59 x 10 -1
3. (2 .8x 10 -9 )(4.75 x 10 -3 )
plz hurry
Answers
Related Questions
Order the set of numbers from least to greatest.
{1, -2.5, 0.75, 3, -0.75}
Answers
Answer:
-2.5, -0.75, 0.75, 1, 3.
What does (MAD) mean?
Answers
Hey!!!
MAD stands for Mean Absolute Deviation.
Explanation:
Mean Absolute Deviation (MAD) of a data set is the average distance between each data value and the mean.
Hope it helps..
Good luck on your assignment
Answer:
(MAD) is an abbreviation of mean absolute deviation.
PLEASE HELP I AM GROUNDED AND MY MOTHER IS SO MAD AT ME FOR MY GRADE

Answers
Answer: b=116, c=64
Step-by-step explanation:
You are building a shelf that fits in a corner. In the figure, the entire shelf is 2 points ABC. If each unit in the coordinate plane represents one inch, then the
AREA of the shelf is
square inches. A(20,30) B(20,10) C(10,10)
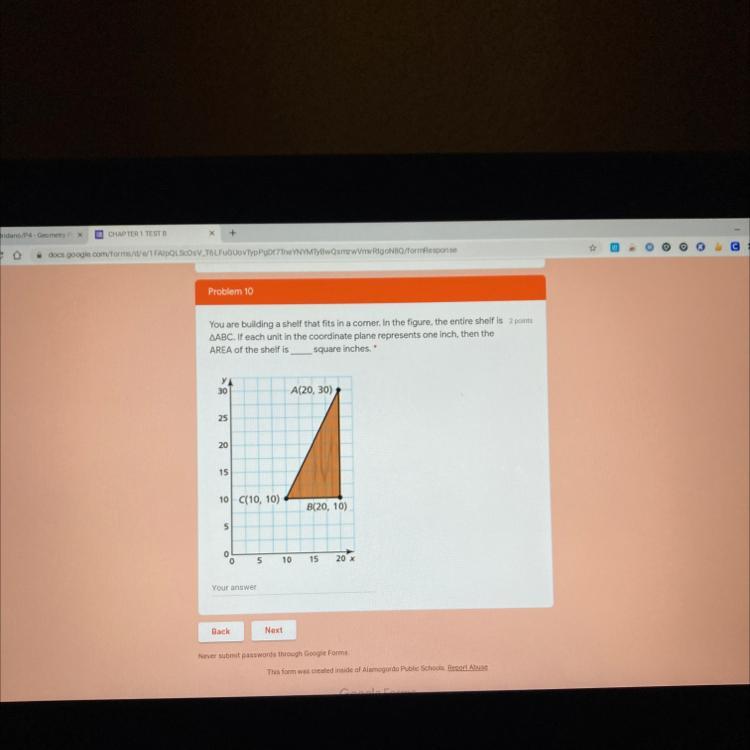
Answers
Answer:
100 square inches
Step-by-step explanation:
The width of the shelf is BC = 20 - 10 = 10 inches.
The height of the shelf is AB = 30 - 10 = 20 inches.
The area of a triangle with these dimensions is ...
A = (1/2)bh
A = (1/2)(10 in)(20 in) = 100 in^2
The area of the shelf is 100 square inches.
Gloria checked her gas mileage and found that she had used 16.6 gal of gas to travel 372 miles. At this rate, how many gallons will she use to travel from San Antonio to Las Vegas, a distance of 1,284 miles?
round the answer to the nearest whole number
Answers
Answer:
58 gallons of gas
Step-by-step explanation:
1,284/372= 3.5 Rounded
16.6 * 3.5= 58.1 gallons of gas
38
21
21
X
What is the value of X
Answers
Answer:
80
Step-by-step explanation:
honestly it depends on the question but if it's addition, this is the answer
what is the area of a semicircle that has a radius of 30 feet
Answers
Answer:
A = 1413.72 unit²
Step-by-step explanation:
area of a semicircle formula: A = (πr²)/2
To find the area of a semicircle that has a radius of 30 feet, apply r = 30 to the formula A = (πr²)/2:
A = (π30²)/2
A = 1413.72 unit²
Alice is willing to spend $30 on a pair of jeans and has a coupon for $10 off she found online. She selects and purchases a $35 pair of jeans, pre-discount. Determine whether this would create a producer or consumer surplus and calculate the ensuing surplus.
Answers
Consumer surplus $5 as we solve the Q by given data
Consumer surplus is the difference between the consumer's willingness to pay and the price of the commodity.
Consumer surplus in economics, also called social surplus or consumer surplus, is the difference between the price a consumer pays for a commodity and the price the consumer is willing to pay in exchange for giving it up.
Producer surplus is the difference between the price of a commodity and the lowest price at which a seller is willing to sell it.
Consumer Surplus = Willingness to Pay - Price of the Good.
Item Price = $35 - $10 = $25
$30 - $25 = $5
Producer surplus is the difference between the price of a commodity and the lowest price at which a seller is willing to sell it.
know more about consumer surplus click here;
https://brainly.com/question/14852681
#SPJ4
Find the exact value and the approximate value of the perimeter of the triangle

Answers
the perimeter of triangle is equal to the sum of all the side of the triangle,
The perimeter of given triangle is x+y+9+3
Solve for x and y,
Apply pythagoras theorem in triangle ADC,
\(\begin{gathered} AC^2=DC^2+AD^2 \\ y^2=81+AD^2^{} \\ AD^2=y^2-81 \end{gathered}\)Now, in triangle ADB
Apply pythagoras,
\(\begin{gathered} AB^2^{}=BD^2+AD^2 \\ x^2=9+AD^2 \\ AD^2=x^2-9 \end{gathered}\)Compare the value of AD from both the equation,
\(\begin{gathered} x^2-9=y^2-81 \\ x^2-y^2=-72 \end{gathered}\)Now, in triangle ABC
\(\begin{gathered} BC^2=AB^2+AC^2 \\ 12^2=x^2+y^2 \\ x^2+y^2=144 \end{gathered}\)Add the equation
\(\begin{gathered} x^2+x^2-y^2+y^2=-72+144 \\ 2x^2=72 \\ x^2=36 \\ x=6 \end{gathered}\)Substitute x=6 in the above equation,
\(\begin{gathered} x^2_{}+y^2=144 \\ 36+y^2=144 \\ y^2=144-36 \\ y^2=108 \\ y=10.39 \end{gathered}\)So, the value of the other side of triangle are 6, 10.39
Perimeter of triangle =sum of all sides of triangle
\(\begin{gathered} \text{Perimeter}=AB+BC+AC \\ \text{Perimeter}=AB+BD+CD+AC \\ \text{Perimeter}=6+3+9+10.39_{} \\ \text{Perimeter}=28.39 \end{gathered}\)ANSWER : Perimeter is 28.39

How much money will Shawn have in the bank after 5 years if he invests $1000 at a rate of 3% compounded quarterly? Which equation represents the situation?

Answers
The future value that Shawn will have in the bank after 5 years of investing $1,000 at a rate of 3% compounded quarterly is $1,161.18.
The equation that represents the situation is B) A = 1,000 (1.0075)⁴ˣ⁵
What is the future value?The future value describes the compounded present value at an interest rate.
The future value can be determined using the above FV formula or equation or an online finance calculator as follows:
N (# of periods) = 20 quarters (5 years x 4)
I/Y (Interest per year) = 3%
PV (Present Value) = $1,000
PMT (Periodic Payment) = $0
Results:
Future Value (FV) = $1,161.18
Total Interest = $161.18
Learn more about the future value at https://brainly.com/question/24703884.
#SPJ1
Describe and correct the error a student made in finding the midpoint cd with c(-4,5) and d(-1,-4).
Answers
Answer:
Step-by-step explanation:
The formula for finding the midpoint of two coordinates is expressed as;
M(X,Y) = \((\frac{x_1+x_2}{2} , \frac{y_1+y_2}{2})\)
Given the coordinates c(-4,5) and d(-1,-4), x1 = -4, y1 = 5, x2 = -1 and y2 = -4.
For the X coordinate of the midpoint
X = x1+x2/2
X = -4+(-1)/2
X = -4-1/2
X = -5/2
X = -2.5
Similarly for Y:
Y = y1+y2/2
Y = 5+(-4)/2
Y = 5-4/2
Y = 1/2
Y = 0.5
Hence the midpoint coordinate of C(-4,5) and D (-1,-4) is (-2.5, 0.5)
Dr. W Sweet Rides Car Rental charges a flat fee of $24 and an additional $0.35 for every mile the car is driven. Which function models the total cost, C(x), of renting a car for x miles?
Answers
Answer:
\(c = 0.35 x + 24\)
Step-by-step explanation:
First, let's go over the information we have. We know that no matter what, Dr. W Sweet will charge a base fee of $24, and that for each additional mile, he will charge 35¢. Now let's make an equation reflecting this information:
cost = 35¢ (number of miles) + $24 (starting fee)
We can also write this like this:
\(c = 0.35x + 24\)
If you want to test this equation, put in a value for the x variable, like so:
Value: 25 miles
\(c = 0.35(25) + 24 \\ c = 8.75 + 24 \\ c = 32.75\)
For this situation, the cost will be $32.75. I hope this helps! If you have questions, comment on this response, I should write back reasonably quickly.
i dont get this please help with the explanation and steps

Answers
XZ is 11 unit away from each other so middle of it will be 2.5
Find the distance between the two points in simplest radical form.

Answers
The distance bewteen the points (-3,5) and (3,1) in a simple radical form is 2√13.
What is the distance between the given points?The distance formula used in finding the distance between two points is expressed as;
d = √( ( x₂ - x₁ )² + ( y₂ - y₁ )² )
From the graph;
Point A: (-3,5)
x₁ = -3
y₁ = 5
Point B: (3,1)
x₂ = 3
y₂ = 1
Plug the given values into the distance formula and simplify.
\(d = \sqrt{( x_2 - x_1)^2 + (y_2 -y_1 )^2} \\\\d = \sqrt{( 3-(-3))^2 + (1 -5)^2} \\\\d = \sqrt{( 3+ 3)^2 + (1 -5)^2} \\\\d = \sqrt{( 6)^2 + (-4)^2} \\\\d = \sqrt{36 + 16} \\\\d = \sqrt{52}\\\\d = 2\sqrt{13}\)
Therefore, the distance between the points is 2√13.
Learn more about the distance formula here: brainly.com/question/24509115
#SPJ1
PLEASE HURRY AND HELPPPP!!
In order to prove that the diagonals of a rhombus are perpendicular to each other using the following figure, which triangle congruency postulate is used?

Answers
Answer:
SSS Postulate
Step-by-step explanation:
Just took the test ;)
use l'hopital's rule to show that the sequence whose nth term is converges. to what number converges?group of answer choices- 43- 10
Answers
The sequence whose nth term is (2n+1)/(3n-1) converges to the number 2/3.
To use L'Hopital's rule, we need to take the limit of the ratio of the nth term and (n-1)th term as n approaches infinity.
Let a_n be the nth term of the sequence. lim (n->∞) a_n / a_(n-1) = lim (n->∞) (2n+1)/(3n-1) / (2n-1)/(3n-4) = lim (n->∞) [(2n+1)/(3n-1)] * [(3n-4)/(2n-1)] = lim (n->∞) [6n^2 - 5n - 4]/[6n^2 - 7n + 4]
By applying L'Hopital's rule, we can find that the limit of this ratio as n approaches infinity is 1. Thus, the sequence converges to the same limit as the ratio of consecutive terms, which is 2/3.
Visit here to learn more about Sequence:
brainly.com/question/7882626
#SPJ11
If you were to measure all the teams and find the average height of each team, then this would be a called a sampling distribution. What would be true about this collection of sample averages
Answers
The collection of sample averages, known as the sampling distribution, would have an average that is equal to the average height of the entire population.
When measuring the height of each team and calculating their average, we are essentially taking samples from the population of all teams. The sampling distribution is created by repeating this process multiple times and calculating the average for each sample. According to the central limit theorem, as the sample size increases, the sampling distribution approaches a normal distribution regardless of the shape of the population distribution.
Therefore, the average of the sampling distribution, which represents the average height of all teams, would be equal to the average height of the entire population. The sampling distribution allows us to make inferences about the population based on the collected samples and provides a measure of the variability of the sample averages.
To know more about sampling distribution follow the link:
https://brainly.com/question/29368683
#SPJ11
In quadrilateral qrst, angle r s t measures (5x 15)°. angle tqr measures (4x 3)°. circle p is inscribed with quadrilateral q r s t. what is the measure of angle rst?
Answers
The measure of the angle rst is \(105^{o}\).
What is the inscribed quadrilateral theorem?According to the theorem, a quadrilateral can be inscribed by a circle if and only if its opposing angles are supplementary. A quadrilateral that may be encircled by a circle is known as a cyclic quadrilateral.
The sum opposite angles of a quadrilateral is 180 degrees.
We can see that the angles rst and angle tqr are opposite angles of quadrilateral qrst, hence supplementary angles.
Therefore,
<RST + <TQR = 180
5x+15 + 4x+ 3 = 180
9x + 18 = 180
9x = 180 - 18
9x = 162
x = 162/9
x = 18
Since <RST = 5x+15
<RST = 5(18) + 15
<RST = 90 + 15
<RST = 105degrees
Learn more about cyclic quadrilateral at: https://brainly.com/question/14352697
#SPJ4
Please help me, only 20 points if answered !!

Answers
\(\textit{arc's length}\\\\ s = \cfrac{\theta \pi r}{180} ~~ \begin{cases} r=radius\\ \theta =\stackrel{degrees}{angle}\\[-0.5em] \hrulefill\\ r=4\\ s=\pi \end{cases}\implies \pi =\cfrac{\theta \pi (4)}{180}\implies \cfrac{180}{4\pi }\cdot \pi =\theta\implies 45=\theta\)
Convert to an equation in rectangular coordinates.r = 4 /cos (theta) - sin (theta). (Express numbers in exact form. Use symbolic notation and fractions where needed.) equation: _____. Explain your reasoning: 500 Characters remaining
Answers
This equation relates the rectangular coordinates x and y to the polar angle theta, and describes the curve traced out by the polar equation in the x-y plane.
To convert the polar equation \(r = 4 /cos (\theta) - sin (\theta)\) to rectangular coordinates, we can use the following trigonometric identities:
\(cos(\theta) = x/r\)
\(sin(\theta) = y/r\)
where x and y are the rectangular coordinates of the point.
Substituting these values in the given equation, we get:
r = 4 / (x/r) - y/r
\(r^2 = 4r/x - y\)
\(x^2 + y^2 = 4r - ry\)
Now, we can use the identity \(r^2 = x^2 + y^2\) to substitute for r in the above equation and simplify:
\(x^2 + y^2 = 4(4/cos(\theta) - sin(\theta)) - y(4/cos(\theta) - sin(\theta))\)
\(x^2 + y^2 = (16 - 4sin(\theta))/cos(\theta) - y(4/cos(\theta) - sin(\theta))/cos(\theta)\)
Multiplying both sides by cos(theta), we get:
\(x^2cos(\theta) + y^2cos(\theta) = 16 - 4sin(\theta) - y(4 - sin(\theta))\)
\(x^2cos(\theta) + y^2cos(\theta) + ysin(\theta) = 16 - 4sin(\theta)\)
Therefore, the equation in rectangular coordinates is:
\(x^2cos(\theta) + y^2cos(\theta) + ysin(\theta) = 16 - 4sin(\theta)\)
This equation relates the rectangular coordinates x and y to the polar angle theta, and describes the curve traced out by the polar equation in the x-y plane.
To learn more about polar equation visit:https://brainly.com/question/1269731
#SPJ11
Matilda has 16 3/4 hours to finish three consulting projects.how much time may she spend on each project ,if she plans to spend the same amount of time on each?
Answers
Time taken by Matilda on each project is \(5\frac{7}{12}\) hours.
According to the question we have been given that,
Total time taken by Matilda to complete the consulting projects = \(16\frac{3}{4}\) hours
First we will convert it into simple fraction which is
\(16\frac{3}{4} = \frac{67}{4} \\\) hours
Number of consulting projects = 3
And Matilda spends same amount of time to each of the project.
To find the time she spend on each project is by using unitary method
that is, 3 projects = \(\frac{67}{4}\) hours
1 project = \(\frac{67}{4} / 3\)
= 67/12
= \(5\frac{7}{12}\) hours
Hence time taken by Matilda on each project is \(5\frac{7}{12}\) hours.
Learn more about unitary method here : https://brainly.com/question/24587372
#SPJ4
A rectangle is transformed according to the rule R0, 90º. The image of the rectangle has vertices located at R'(–4, 4), S'(–4, 1), P'(–3, 1), and Q'(–3, 4). What is the location of Q?
(–4, –3)
(–3, –4)
(3, 4)
(4, 3)
Answers
Answer:
A
Step-by-step explanation:
i think...
The transformation is (4, 3)
what is transformation?A transformation is a general term for four specific ways to manipulate the shape and/or position of a point, a line, or geometric figure. The original shape of the object is called the Pre-Image and the final shape and position of the object is the Image under the transformation
If the there is rotation of 90° around the origin (0,0), that can be expressed as
(x, y) => (-y, x)
Which means a 90° rotation that can done by changing coordinates positions and inverting the sign of y-coordinate.
However, the problem is giving the transformed coordinates where
Q'(–3, 4)
Hence, the transformation is (4, 3)
Learn more about transformations here:
https://brainly.com/question/10519316
#SPJ6
Find the perimeter of the right triangle. If necessary, round to the nearest tenth.
19 cm
20 cm
a.
27. 6 cm
b. 190 cm
c. 66. 6 cm
d. 39 cm
Please select the best answer from the choices provided
Answers
The perimeter of the right triangle is 66.6 cm (rounded to the nearest tenth)Option C is the correct answer.
The given two sides are 19 cm and 20 cm and we need to find the perimeter of the right triangle. We know that the hypotenuse is given by c = √(a²+b²).
The term "perimeter" describes the overall length of a two-dimensional shape's boundary or outer edge. The lengths of all the sides or segments that make up the shape's outline are added to determine it. The distance surrounding an object or the enclosure of an area can be determined by its perimeter. Measurement and comparison of the dimensions of polygons like squares, rectangles, triangles, and circles are frequently employed in geometry. In many \(\sqrt{a^2+b^2}\)everyday situations, such as constructing a fence for a garden, calculating the amount of building materials required, or calculating the distance travelled along a route, knowing a shape's perimeter is crucial.
Let's first find the hypotenuse of the right triangle.The hypotenuse is given by:c = \(\sqrt{(a^2+b^2)c} = \sqrt{19^2+20^2)c}\) = \(\sqrt{(361+400)c} = \sqrt{761c }\)= 27.568Which rounds off to 27.6 cm (rounded to the nearest tenth).The perimeter of the right triangle is given by:
P = a + b + cP = 19 + 20 + 27.6P = 66.6
Therefore, the perimeter of the right triangle is 66.6 cm (rounded to the nearest tenth)Option C is the correct answer.
Learn more about perimeter here:
https://brainly.com/question/7486523
#SPJ11
1) Given a triangle ABC, such that: BC = 6 cm; ABC = 40° and ACB = 60°. 1) Draw the triangle ABC. 2) Calculate the measure of the angle BAC. 3) The bisector of the angle BAC intersects [BC] in a point D. Show that ABD is an isosceles triangle. 4) Let M be the midpoint of the segment [AB]. Show that (MD) is the perpendicular bisector of the segment [AB]. 5) Let N be the orthogonal projection of D on (AC). Show that DM = DN.
Answers
Step-by-step explanation:
1) To draw triangle ABC, we start by drawing a line segment BC of length 6 cm. Then we draw an angle of 40° at point B, and an angle of 60° at point C. We label the intersection of the two lines as point A. This gives us triangle ABC.
```
C
/ \
/ \
/ \
/ \
/ \
/ \
/ \
/_60° 40°\_
B A
```
2) To find the measure of angle BAC, we can use the fact that the angles in a triangle add up to 180°. Therefore, angle BAC = 180° - 40° - 60° = 80°.
3) To show that ABD is an isosceles triangle, we need to show that AB = AD. Let E be the point where the bisector of angle BAC intersects AB. Then, by the angle bisector theorem, we have:
AB/BE = AC/CE
Substituting the given values, we get:
AB/BE = AC/CE
AB/BE = 6/sin(40°)
AB = 6*sin(80°)/sin(40°)
Similarly, we can use the angle bisector theorem on triangle ACD to get:
AD/BD = AC/BC
AD/BD = 6/sin(60°)
AD = 6*sin(80°)/sin(60°)
Since AB and AD are both equal to 6*sin(80°)/sin(40°), we have shown that ABD is an isosceles triangle.
4) To show that MD is the perpendicular bisector of AB, we need to show that MD is perpendicular to AB and that MD bisects AB.
First, we can show that MD is perpendicular to AB by showing that triangle AMD is a right triangle with DM as its hypotenuse. Since M is the midpoint of AB, we have AM = MB. Also, since ABD is an isosceles triangle, we have AB = AD. Therefore, triangle AMD is isosceles, with AM = AD. Using the fact that the angles in a triangle add up to 180°, we get:
angle AMD = 180° - angle MAD - angle ADM
angle AMD = 180° - angle BAD/2 - angle ABD/2
angle AMD = 180° - 40°/2 - 80°/2
angle AMD = 90°
Therefore, we have shown that MD is perpendicular to AB.
Next, we can show that MD bisects AB by showing that AM = MB = MD. We have already shown that AM = MB. To show that AM = MD, we can use the fact that triangle AMD is isosceles to get:
AM = AD = 6*sin(80°)/sin(60°)
Therefore, we have shown that MD is the perpendicular bisector of AB.
5) Finally, to show that DM = DN, we can use the fact that triangle DNM is a right triangle with DM as its hypotenuse. Since DN is the orthogonal projection of D on AC, we have:
DN = DC*sin(60°) = 3
Using the fact that AD = 6*sin(80°)/sin(60°), we can find the length of AN:
AN = AD*sin(20°) = 6*sin(80°)/(2*sin(60°)*cos(20°)) = 3*sin(80°)/cos(20°)
Using the Pythagorean theorem on triangle AND, we get:
DM^2 = DN^2 + AN^2
DM^2 = 3^2 + (3*sin(80°)/cos(20°))^2
Simplifying, we get:
DM^2 = 9 + 9*(tan(80°))^2
DM^2 = 9 + 9*(cot(10°))^2
DM^2 = 9 + 9*(tan(80°))^2
DM^2 = 9 + 9*(cot(10°))^2
DM^2 = 9 + 9*(1/tan(10°))^2
DM^2= 9 + 9*(1/0.1763)^2
DM^2 = 9 + 228.32
DM^2 = 237.32
DM ≈ 15.4
Similarly, using the Pythagorean theorem on triangle ANC, we get:
DN^2 = AN^2 - AC^2
DN^2 = (3*sin(80°)/cos(20°))^2 - 6^2
DN^2 = 9*(sin(80°)/cos(20°))^2 - 36
DN^2 = 9*(cos(10°)/cos(20°))^2 - 36
Simplifying, we get:
DN^2 = 9*(1/sin(20°))^2 - 36
DN^2 = 9*(csc(20°))^2 - 36
DN^2 = 9*(1.0642)^2 - 36
DN^2 = 3.601
Therefore, we have:
DM^2 - DN^2 = 237.32 - 3.601 = 233.719
Since DM^2 - DN^2 = DM^2 - DM^2 = 0, we have shown that DM = DN.
according to the national institute on drug abuse, a u.s. government agency, 17.3% of 8th graders in 2010 had used marijuana at some point in their lives. a school official hopes to show the percentage is lower in his district, testing : versus : . the health department for the district uses anonymous random sampling and finds that 10% of 80 eighth-graders surveyed had used marijuana. are conditions met for use of the normal model to represent the distribution of sample proportions?
Answers
according to the national institute on drug abuse, a u.s. government agency, 17.3% of 8th graders in 2010 had used marijuana at some point in their lives . Since all three conditions are satisfied, we can use the normal model to represent the distribution of sample proportions
Randomness: The sample must be selected randomly from the population. The problem states that the health department for the district uses anonymous random sampling, so the randomness condition is satisfied.
Independence: The sample size must be less than 10% of the population size. The problem does not give us the population size, but since the sample size is 80 and we are dealing with eighth-graders in a district, it is reasonable to assume that the population size is much larger than 800.
Success-Failure: The number of successes and failures in the sample must be at least 10. The number of eighth-graders in the sample who have used marijuana is 0.1 x 80 = 8. Both of these numbers are greater than 10, so the success-failure condition is also satisfied.
To learn about drug abuse visit:
https://brainly.com/question/11607765
#SPJ4
Sue ate one sweetie one day, and each day afterward she ate one sweetie more than she did the day before. How many sweeties did she eat during her first week?
Answers
Answer:
28
Step-by-step explanation:
1 + 2 + 3 + 4 + 5 + 6 + 7
A car traveled 3⁄4 mile in one minute at constant speed. What was the speed of the car in miles per hour?
Answers
Answer:
45 mph
Step-by-step explanation:
3/4x60=45
In a shooting game, a player is given 5 points when he hits the target and 3 points are deducted when he misses the target. Singam missed the target for x times out of 50 trials. If his final score is 122 points, calculate the value of x
Answers
Singam missed the target 16 times in the shooting game
How to find the value of xAssumng A be the number of times Singam hits the target and x be the number of times he misses the target
then
A + x = 50
5A - 3x = 122
finding A in terms of x
A = 50 - x
Substituting and simplifying
5 * (50 - x) - 3x = 122
250 - 8x = 122
8B = 128
x = 16
Learn more about word problems at
https://brainly.com/question/21405634
#SPJ1
what is the electrical work done in a circuit
Answers
Answer:
a open and close switch and a condentation out put.
find the domain and range

Answers
Answer:
B.
Step-by-step explanation: