you set up a colorful candy bag for your friend with 4 cherry, 8 orange, 2 lemon, 8 grape, and 6 sour raspberry, hard candies. when they pull out two of them, one for each of you, what is the probability they draw 1 cherry and 1 sour raspberry in either order?
Answers
Answer:
Step-by-step explanation:
The total number of candies in the bag is 4 cherry + 8 orange + 2 lemon + 8 grape + 6 sour raspberry = 28 candies.
The probability of drawing a cherry on the first draw is 4/28, and the probability of drawing a sour raspberry on the second draw given that a cherry was drawn first is 6/27 (since there are 27 candies left in the bag after the first draw).
The probability of drawing a sour raspberry on the first draw is 6/28, and the probability of drawing a cherry on the second draw given that a sour raspberry was drawn first is 4/27.
Therefore, the probability of drawing one cherry and one sour raspberry in either order is:
(4/28) * (6/27) + (6/28) * (4/27) = 24/756 + 24/756 = 48/756
So the probability of drawing one cherry and one sour raspberry in either order is 48/756.
Related Questions
Pleaseeeee help!!!!!

Answers
Answer:
.71
Step-by-step explanation:
We only need to look at the brown eyes row
2+2+10 =14
Brown hair is 10
P(brown hair) = brown hair / total
=10/14 =5/7 = .714285714
Help me with this question

Answers
Answer:
Around 25.8 square units
Step-by-step explanation:
\(A=\dfrac{1}{2}(5)(18)(\sin 35)=\\\\45\cdot \sin 35\approx 25.8\)
Hope this helps!
Write an explicit formula for a(n) the n^th term of the sequence 8,24,72,
Answers
Answer:
multiplying the previous term in the sequence by 33 gives the next term. In other words, an=a1⋅rn−1an=a1⋅rn-1.
Geometric Sequence: r=3
vertex form of y=-2x^2+16x-24
Answers
Laura and Rich have been approved for a $325,000, 15-year mortgage with an APR of 5.3%. Using the mortgage and interest formulas, complete the two-month amortization table.
Answers
First, let's calculate the monthly interest rate (i), which is the APR divided by 12 months:
i = APR / 12 months
i = 5.3% / 12
i = 0.00442 or 0.442%
Next, let's calculate the number of months (n) for the mortgage, which is 15 years multiplied by 12 months:
n = 15 years x 12 months/year
n = 180 months
Now, let's calculate the monthly payment (PMT) using the following formula:
PMT = P * i / \((1 - (1 + i)^(-n)\))
where P is the principal amount, i is the monthly interest rate, and n is the number of months.
PMT = $325,000 * 0.00442 / (1 - \((1 + 0.00442)^(-180)\)
PMT = $2,613.67 (rounded to the nearest cent)
Now, let's create the amortization table for the first two months:
Month | Payment | Interest | Principal | Remaining Balance
1 | $2,613.67 | $1,431.25 | $1,182.42 | $323,817.58
2 | $2,613.67 | $1,428.60 | $1,185.07 | $322,632.51
For each month, the Payment column shows the fixed monthly payment, the Interest column shows the calculated interest based on the remaining balance multiplied by the monthly interest rate, the Principal column shows the portion of the payment that goes towards reducing the principal, and the Remaining Balance column shows the remaining balance after subtracting the principal payment from the previous remaining balance.
The amortization table will continue in this manner for the remaining months until the mortgage is paid off.
Learn more about “ monthly interest rate “ visit here;
https://brainly.com/question/11916359
#SPJ4
The interest and principal amounts for the first payment are:
Interest = $325,000 * 0.0044167 = $1,426.25
Principal = $2,549.67 - $1,426.25 = $1,123.42
Balance = $325,000 - $1,123.42 = $323,876.58
For the second payment, we start with the new balance of $323,876.58 and apply the formulas again:
Interest = $323,876.58 * 0.0044167 = $1,420.47
Principal = $2,549.67 - $1,420.47 = $1,129.20
Balance = $323,876.58 - $1,129.20 = $322,747.38
To complete the two-month amortization table, we need to calculate the monthly payment, as well as the principal and interest amounts for each payment.
The formula for calculating a fixed-rate mortgage payment is:
\(Payment = P * r * (1 + r)^n / [(1 + r)^n - 1]\)
Where:
P = Principal amount borrowed
r = Monthly interest rate
n = Total number of payments
First, let's calculate the monthly interest rate.
Since the APR is an annual rate, we need to divide it by 12 to get the monthly rate:
Monthly interest rate = 5.3% / 12 = 0.0044167
Next, we need to calculate the total number of payments.
Since this is a 15-year mortgage, and we're completing a two-month amortization table, the total number of payments is:
Total number of payments = 15 years * 12 months per year = 180
Number of payments for two months = 2
Now we can plug these values into the formula to calculate the monthly payment:
Payment = \($325,000 * 0.0044167 * (1 + 0.0044167)^180 / [(1 + 0.0044167)^180 - 1]\)
= $2,549.67
So the monthly payment is $2,549.67
Now we can use this value to complete the two-month amortization table:
Payment Interest Principal Balance
Month 1 $1,426.25 $1,123.42 $323,876.58
Month 2 $1,420.47 $1,129.20 $322,747.38
To calculate the interest and principal amounts for each payment, we use the following formulas:
Interest = Balance * Monthly interest rate
Principal = Payment - Interest
Balance = Balance - Principal
We start with the initial balance of $325,000 and apply the formulas for each payment.
The interest and principal amounts for the first payment are:
Interest = $325,000 * 0.0044167 = $1,426.25
Principal = $2,549.67 - $1,426.25 = $1,123.42
Balance = $325,000 - $1,123.42 = $323,876.58
For the second payment, we start with the new balance of $323,876.58 and apply the formulas again:
Interest = $323,876.58 * 0.0044167 = $1,420.47
Principal = $2,549.67 - $1,420.47 = $1,129.20
Balance = $323,876.58 - $1,129.20 = $322,747.38
And so on, for each subsequent payment.
For similar question on amortization.
https://brainly.com/question/29485954
#SPJ11
The equation of line m is y=3 x-1 . What is the equation of a line that goes through the point (3,-2) and is perpendicular to line m ? Show your work.
Answers
The equation of the line that is perpendicular to line m and passes through the point (3,-2) is y = -1/3 x - 1.
To find the equation of a line that is perpendicular to line m, we need to determine the negative reciprocal of the slope of line m. The slope of line m is 3. The negative reciprocal of 3 is -1/3. Therefore, the slope of the perpendicular line is -1/3.
Next, we can use the point-slope form of a linear equation to find the equation of the perpendicular line. The point-slope form is given by y - y1 = m(x - x1), where (x1, y1) is a point on the line and m is the slope.
Plugging in the values from the given point (3, -2) and the slope -1/3, we have y - (-2) = -1/3(x - 3). Simplifying this equation gives y + 2 = -1/3x + 1. Rearranging the terms, we get y = -1/3x - 1. Therefore, the equation of the line that is perpendicular to line m and passes through the point (3, -2) is y = -1/3x - 1.
Learn more about point-slope here:
https://brainly.com/question/837699
#SPJ11
Ethan is watering his plants. He starts with a watering can filled with 32 ounces of water, and he pours 3.5 ounces onto each plant. When Ethan finishes watering his plants, he has 14.5 ounces of water left. How many plants does he have? Write and solve an equation to find the answer.
Answers
The number of plants Ethan has are 5.
What is Equation?Two or more expressions with an Equal sign is called as Equation.
Let x be the number of plants Ethan has.
Ethan uses 3.5 ounces of water for each plant, so he will use a total of 3.5p ounces of water.
If he starts with 32 ounces of water and ends up with 14.5 ounces
Total of 32 - 14.5 = 17.5 ounces of water.
As given the amount of water used is equal to the amount of water per plant times the number of plants:
3.5x = 17.5
Divide both sides by 3.5
x=5
Hence, , Ethan has 5 plants.
To learn more on Equation:
https://brainly.com/question/10413253
#SPJ9
there were 252 people at the concert . If 90% of the seats were filled, how many seats are in the auditorium?
Answers
Answer:
280 seats total
Step-by-step explanation:
90/100 = 252/x
To find x, cross multiply.
90x = 25,200
Divide both sides by 90 to get the variable alone.
x = 280 seats
Once we have categorized an object, our memory of the object increasingly resembles thecategoryA) algorithm.B) prototype.C) heuristic.D) mental set
Answers
Once we have categorized an object, our memory of the object increasingly resembles the category is B) prototype. This means that when we categorize an object, our memory of it begins to resemble the prototype or typical example of that category. For example, if we categorize a bird as a robin, our memory of the bird will increasingly resemble the characteristics of a typical robin.
This happens because our brain uses prototypes as a shortcut to process information and make sense of the world around us. We use prototypes to quickly identify objects and make assumptions about their characteristics based on their category.
our memory of an object after categorization is influenced by the prototype of the category. This helps us to quickly process and make sense of information, but it can also lead to errors and biases in our thinking.
A prototype is a mental image or best example of a category. When we categorize an object, our memory of the object increasingly resembles the prototype because we tend to recall the most representative or typical example of the category.
Once we categorize an object, our memory of the object becomes more like the prototype, which is the best example of the category. This is because we tend to remember the most representative or typical examples of a category.
To know more about prototype, visit:
https://brainly.com/question/28187820
#SPJ11
The most common purpose for Pearson correlational is to examine
Answers
For Pearson correlation the most common purpose to examine is given by option a. The relationship between 2 variables.
The Pearson correlation is a statistical measure that indicates the extent to which two continuous variables are linearly related.
It measures the strength and direction of the relationship between two variables.
Ranging from -1 perfect negative correlation to 1 perfect positive correlation.
And with 0 indicating no correlation.
It is commonly used in research to examine the association between two variables.
Such as the relationship between height and weight, or between income and education level.
Therefore, the most common purpose of a Pearson correlation is to examine the relationship between 2 variables.
learn more about correlation here
brainly.com/question/30433001
#SPJ4
The above question is incomplete, the complete question is:
The most common purpose for a Pearson correlation is to examine,
a. The relationship between 2 variables
b. Relationships among groups
c. Differences between variables
d. Differences between two or more groups
Which of the following domains are closed and which are bounded?
(a) {(x,y)∈R2:x2+y2≤1}
(b) {(x,y)∈R2:x2+y2<1}
(c) {(x,y)∈R2:x≥0}
(d) {(x,y)∈R2:x>0,y>0}
(e) {(x,y)∈R2:1≤x≤4,5≤y≤10}
(f) {(x,y)∈R2:x>0,x2+y2≤10}
Answers
(a) The domain closed and bounded.
(b) The domain bounded.
(c) The domain closed.
(d) The domain bounded.
(e) The domain closed and bounded.
(f) The domain closed and bounded.
In this question, we have been given some domains.
We need to check which domains are closed and which are bounded.
A domain of function is said to be closed if the region R contains all boundary points.
A bounded domain is nothing but a domain which is a bounded set.
(a) {(x,y)∈R2:x^2+y^2≤1}
The domain of x^2+y^2≤1 contains set of all points (x, y) ∈R2
so, the domain closed and bounded.
(b) {(x,y)∈R2:x2+y2<1}
The domain of x^2+y^2 < 1 contains set of all points (x, y) ∈R2
so, the domain is bounded.
(c) {(x,y)∈R2: x ≥ 0}
The domain of x ≥ 0 is R2 - {x < 0}
So, the domain is closed.
(d) {(x, y) ∈ R2 : x > 0,y > 0}
The domain is R2 - {(x, y) ≥ 0}
So, the domain is bounded.
(e) {(x, y) ∈ R2 : 1 ≤ x ≤ 4, 5 ≤ y ≤ 10}
The domain is closed and bounded.
(f) {(x,y)∈R2:x>0,x^2+y^2≤10}
The domain is closed and bounded.
Learn more about the domain here:
https://brainly.com/question/28135761
#SPJ4
pumpkins at a local farm sell for $0.49 per pound. remi spent $73.50. how many pounds of pumpkins were purchased?
Answers
Remi purchased approximately 150 pounds of pumpkins.
To find the number of pounds of pumpkins purchased by Remi, we can divide the total amount spent by the price per pound.
Let's assume that x represents the number of pounds of pumpkins purchased.
The total amount spent, $73.50, can be expressed as the product of the price per pound, $0.49, and the number of pounds purchased, x:
$73.50 = $0.49 × x
To solve for x, we divide both sides of the equation by $0.49:
x = $73.50 / $0.49 ≈ 150
Therefore, Remi purchased approximately 150 pounds of pumpkins.
By dividing the total amount spent by the price per pound, we found the quantity of pumpkins purchased.
In this case, Remi spent $73.50 and the price per pound was $0.49, resulting in the purchase of approximately 150 pounds of pumpkins. This information can be useful for budgeting, inventory management, and understanding consumer behavior at the local farm.
Learn more about equation here:
https://brainly.com/question/29018878
#SPJ11
Factor –7x3 + 21x2 + 3x – 9 by grouping. What is the resulting expression?
(3 – 7x)(x2 – 3)
(7x – 3)(3 + x2)
(3 – 7x2)(x – 3)
(7x2 – 3)(3 + x)
Answers
Answer:
(3–7x²)(x–3)
Step-by-step explanation:
If you apply the distributive property in (3–7x²)(x–3), you obtain:
3x-9-7x²(x)+21x²
3x-9-7x³+21x²
When you order the expression, you have:
-7x³+21x²+3x-9
Then, the answer is (3–7x²)(x–3)
The resulting expression from the given algebra after grouping is; C: (3 – 7x²)(x – 3)
What is the resulting algebra expression?We want to simplify the algebraic expression; -7x³ + 21x² + 3x - 9
Applying distributive property of algebra, we have;
-7x²(x - 3) + 3(x - 3)
By factorization, we have;
(3 – 7x²)(x – 3)
Looking at the options, only option C is correct
Read more about Algebra Expression at; https://brainly.com/question/4344214
r is a relation on the set of all nonnegative integers. (a,b) is in r if a and b have the same remainder when divided by 5
Answers
The relation accepts reflexive, symmetry, and transitive.
Recall that a relation R is reflexive if the element (x, x) belongs to R for all elements X in the domain of R.
If (x, y) belongs to R, then follows that (y, x) must likewise belong to R, making the situation symmetric.
And it is transitive if (x, y) and (y, z) belongs to R necessarily implies that (x, z) belongs to R.
Given r is a relation on the set of all nonnegative integers R(a,b)
Reflexive - YES. A given number a will always have the same remainder when divided by 5.
Symmetric - YES. If a and b have the same remainder when divided by 5, then b and a are the same pair, so again they will have the same remainder.
Transitive - YES. If a and b as well as b and c have the same remainder when divided by 5, this is possible if both a and c also have the same remainder when divided by 5.
Therefore the relation accepts reflexive, symmetry, and transitive.
To learn more about reflexive & symmetry visit
https://brainly.com/question/3014815
#SPJ4
PLEASE HELP 30 POINTS! Tara already knew 4 appetizer recipes before starting culinary school, and she will learn 3 new appetizer recipes during each week of school. Write an equation that shows the relationship between the number of weeks and the number of appetizer recipes.
(a) Define your variables.
(b) Write a linear equation that can be used to determine the number of appetizer recipes she will learn during school
(c) Solve your linear equation to determine the number of recipes that Tara will know after 18 weeks in school
(d) Explain your answer to Part 1c.
Answers
I got this:
A: x = number of weeks, y = number of appetizer recipes
B: 4+3x=y
C: 4+3(18)=58
D: 2*18=36
36+18=54
54+4=58
Please help this is my last question will give brailist

Answers
\({\huge{\boxed{\mathfrak{Answer\:with\;explanation}}}\)
Since you can see side \(BC\) which is 48, gets scaled down to 8
We can divide 48 by 8 giving 6
________________________
Now we can just divide side \(AC\) which is 42 by 6 giving us 7
Do the same thing were we divide side \(AB\) which is 24 by 6 giving us 4
________________________
\({\huge{\boxed{\mathfrak{Exact\:Answer}}}\)
________________________
Side \(XY\) is 4 Side \(XZ\) is 7A blue car is 600 kg moving at 5m/s crashes into a red car 400 kg which is initially at rest. After the crash the two cars stick together. What is the initial momentum of the red car before the Collison
Answers
Before the collision, the momentum of the blue car can be calculated as:
p_blue = m_blue * v_blue
p_blue = 600 kg * 5 m/s
p_blue = 3000 kg·m/s
Since the red car is initially at rest, its momentum is zero:
p_red = m_red * v_red
p_red = 0
The total momentum of the system before the collision is therefore:
p_total = p_blue + p_red
p_total = 3000 kg·m/s + 0
p_total = 3000 kg·m/s
After the collision, the two cars stick together and move together as a single object. The final velocity of the combined object can be calculated using the law of conservation of momentum:
p_total = (m_blue + m_red) * v_final
Since the two cars stick together, their masses are added:
m_total = m_blue + m_red
m_total = 600 kg + 400 kg
m_total = 1000 kg
Solving for v_final, we get:
v_final = p_total / m_total
v_final = 3000 kg·m/s / 1000 kg
v_final = 3 m/s
Therefore, after the collision, the combined object (which is now the blue car and the red car stuck together) is moving at a velocity of 3 m/s.
To answer the question, we only need to calculate the initial momentum of the red car before the collision. As we saw earlier, the momentum of the red car before the collision was zero:
p_red = 0
Therefore, the initial momentum of the red car before the collision was zero.
5.
Identify the vertex of the parabola.
A. (6, 3)
B. (3, 0)
C. (4, -1)
D. (5, 0)

Answers
Answer:
B. (3, 0)
Step-by-step explanation:
It's B. (3,0) because it's on the line of 3 and 0 aka x axis
which expression fails to compute the area of a triangle having base b and height h (area is one-half base time height)?
Answers
The expression fails to compute the area of a triangle having base b and height h is (1.0 /2.0)*b*h.
Therefore the answer is A.
The correct expression to compute the area of a triangle having base b and height h is (1/2) * b * h, or equivalently, 0.5 * b * h.
Expression A is incorrect because it uses floating-point division, which may result in round-off errors or inaccuracies in the computation.
Expression B is the correct expression because it uses integer division and the division by 2 is clear.
Expression C is also correct because it uses floating-point division and the division by 2.0 is clear.
Therefore, both expressions B and C are correct, and expression D is a correct equivalent form of B and C.
To know more on floating-point division
https://brainly.com/question/28462275
#SPJ4
--The question is incomplete, answering to the question below--
"which expression fails to compute the area of a triangle having base b and height h (area is one-half base time height)?
A. (1.0 /2.0)*b*h
B. (1 /2)*b*h
C. (b*h)/2.0
D. 0.5*b*h"
please help me with this question <3

Answers
9514 1404 393
Answer:
a) 30.7 million
b) 1.5% per year
c) 42.0 million
d) 2017
Step-by-step explanation:
a) The initial population is P(0) = 30.7 (million). The exponential term is 1 when t=0, so this number is the multiplier of the exponential term.
__
b) The growth factor is the base of the exponential term: 1.015. The growth rate is the difference between this and 1: 1.015 -1 = 0.015 = 1.5%.
The population is growing by 1.5% per year.
__
c) Fill in the value and do the arithmetic. t=2021 -2000 = 21.
P(21) = 30.7·1.015^21 ≈ 41.968 ≈ 42.0
The population in Canada in 2021 is predicted to be 42.0 million.
__
d) For this we need to solve for t when P(t) = 40.
40 = 30.7·1.015^t
40/30.7 = 1.015^t
Taking logarithms gives ...
log(40/30.7) = t·log(1.015)
t = log(40/30.7)/log(1.015) ≈ 17.773
In 2017, the population is predicted to be less than 40 million; in 2018, it is predicted to be more than 40 million. Canada should anticipate hitting 40 million people in 2017.
_____
Additional comment
The second attachment shows the prediction described here is a little high relative to the actuals in the last few years.


Please help I’m in a hurry

Answers
Answer:
2y ⋅ 2y ⋅ 2y ⋅ y ⋅ y ⋅ y
8y^6
Step-by-step explanation:
(2y^2)^3 is the same as saying 2y ⋅ 2y ⋅ 2y ⋅ y ⋅ y ⋅ y
and (2y^2)^3 simplified is 8y^6
Please mark as brainliest ;)
Answer:
8y^6
Step-by-step explanation:
(2y^2)^3= (2^3)(y^2)^3
=8y^6
Line, Line Segment, Ray...
A) are two - dimensional
B) have no dimension
C) are three-dimensional
D) are one dimensional
Answers
Answer:
A
Step-by-step explanation:
They are all straight paths with end points but a line is never ending but it is still two dimensional
Answer:
D - Are One dimensional
Step-by-step explanation:
Line , Line segments and Ray's are all one dimensional objects
what is the formula of 1,-3/4 and 4,-3
Answers
The formula for slope is,
\(m=\frac{-3-(\frac{-3}{4})}{4-1}\)While mining, Jess found a large metal bar that weighed 40 grams. Jess was also able to
determine that the bar contained 30% copper. How many grams of copper are in the metal
bar? Round your answer to the nearest whole number if necessary.
HELP PLEASE!!!!!!!!!
Answers
Answer:
adasd
Step-by-step explanation:
asdawefawefawfe
Answer:
12
Step-by-step explanation:
0.3*40=12
(can I get brainliest please)
Write the explicit
rule for the nth term.
Then find the 112th term.
{15, 5, -5, -15...}
Answers
Answer:
I believe the answer is 121.
Step-by-step explanation:
Formula: (a)n = a + (n - 1)d
(a)n = nth Term of the Sequence
a = First Term in the Sequence
d = Common Difference
112th = 15 + (112 - 1)-5
112th = 15 + 111 - 5
112th = 121
Answer:
Step-by-step explanation:
{ 15, 5, -5, -15...}
the rule is
\(a_{1} = 15, a_{n} = a_{n-1} -10\)
the 112th term
\(a_{112} = a_{1} + (n-1) *d\\\\a_{112} = 15 + (112 -1) * (-10)\\\\a_{112} = 15 - 1110\\\\a_{112} = -1095\)
In the figure below, AD and AB are tangent to the circle centered at O. The segment DB passes through the center of the circle. Given that AD=10.6 and DB=5.6, find DC.
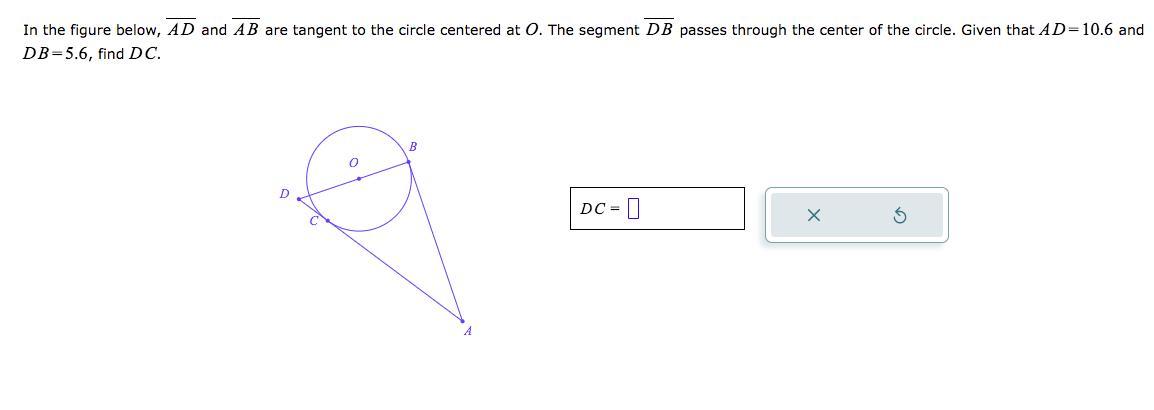
Answers
The length of DC found using Pythagorean theorem given AD = 10.6 and DB = 5.6 and AD and AB are tangent of circle O, is DC = 1.6
How can Pythagorean theorem be used to find DC?The given parameters are;
The tangents of circle O = AD and AB
The segment passing through O = DB
AD = 10.6
DB = 5.6
Required; The length of DC
Solution;
According to Pythagorean theorem, we have;
AB = √(10.6² - 5.6²) = 9
AB = AC = 9
AD = DC + AC
Which gives;
10.6 = DC + 9
DC = 10.6 - 9 = 1.6
Learn more about Pythagorean theorem in geometry here:
https://brainly.com/question/343682
#SPJ1
7. What is the correct value of n if 54 000 000 = 5.4 × 10n.
a.
5
c.
7
b.
6
d.
8
Answers
Answer: b. 6
Step-by-step explanation:
Evaluate the expression when a=6 and b=4. b - 3a
Answers
-14 is the value of the expression b - 3a at a =6 and b = 4.
What is expression?Mathematical expressions consist of at least two numbers or variables, at least one arithmetic operation, and a statement. It's possible to multiply, divide, add, or subtract with this mathematical operation.
Given an expression b - 3a
For this expression given,
a = 6 and b = 4
Thus the value of expression at given values
=> b - 3a
=> 4 - 3 * 6
=>4 - 18
=> -14
Therefore, the value of the expression b - 3a at a =6 and b = 4 is -14.
Learn more about expression here:
https://brainly.com/question/23246712
#SPJ1
How do you find the exact length of the curve y= 7 +1/5 cosh 5x, 0≤x≤2
Answers
The exact length of the curve y = 7 + (1/5)cosh(5x) for 0 ≤ x ≤ 2 is approximately 8.826 units.
To find the exact length of the curve y = 7 + (1/5)cosh(5x) for 0 ≤ x ≤ 2, we need to use the arc length formula:
L = ∫[a,b] sqrt(1 + [f'(x)]^2) dx
where a = 0, b = 2, and f(x) = 7 + (1/5)cosh(5x).
First, we need to find f'(x):
f'(x) = (1/5)*sinh(5x)
Now we can substitute f'(x) and f(x) into the arc length formula:
L = ∫[0,2] sqrt(1 + [f'(x)]^2) dx
L = ∫[0,2] sqrt(1 + (1/25)*sinh^2(5x)) dx
This integral cannot be evaluated in terms of elementary functions, so we need to use a numerical method to approximate the value of the integral. One common numerical method is Simpson's Rule:
L ≈ h/3 [f(x0) + 4f(x1) + 2f(x2) + 4f(x3) + ... + 2f(xn-2) + 4f(xn-1) + f(xn)]
where h = (b-a)/n and n is an even integer.
Using n = 10, we can calculate the approximate value of the integral:
h = (2-0)/10 = 0.2
L ≈ 0.2/3 [f(0) + 4f(0.2) + 2f(0.4) + 4f(0.6) + 2f(0.8) + 4f(1) + 2f(1.2) + 4f(1.4) + 2f(1.6) + 4f(1.8) + f(2)]
L ≈ 8.826
Therefore, the exact length of the curve y = 7 + (1/5)cosh(5x) for 0 ≤ x ≤ 2 is approximately 8.826 units.
Learn more about curve here
https://brainly.com/question/15122151
#SPJ11
Quadrilateral UVWX is a kite. What is TU?
V
TU =
Submit
U
T
73
48
W
X
Answers
The length of TU is 55 unit.
What are Properties of Kite?Kite has two diagonals that right-angle-intersect one another. A kite's primary diagonal is symmetrical. The diagonal's primary opposed angles are equal. A pair of congruent triangles having a common base can be thought of as the kite.
Given:
As, Kite has 2 diagonals that intersect each other at right angles.
TV = 48 and UV = 73
Using Pythagoras theorem
H² = P² + B²
73² = 48² + TU²
TU² = 5329 - 2304
TU² = 3025
TU = 55 unit
Learn more about Kite here:
https://brainly.com/question/26254939
#SPJ1
