You need to borrow money for gas, so you ask your mother and your sister. You can only borrow money from one of them. Before giving you money, they each say they will make you play a game. Your sister says she wants you to flip a fair coin. She will give you $9 for heads and $21 for tails. Your mother says she wants you to roll a six-sided die. She will give you $5 times the number that appears on the die. Determine the expected value of each game and decide which offer you should take.
Answers
$105 for the dice game.
- > heads = $9
-> tails = $21
^ $9+$21=$30
dice game-
6 sides of a dice, she doubles it by 5.
1*5 + 2*5 + 3*5 + 4*5 + 5*5 + 6*5
^ 5+10+15+20+25+30= 105.
-> $105 for dice game.
you can easily get $9/$21 from your sister, but it won’t be as much from the dice, but you have more risk going with the dice since there’s 6 sides. the highest to get from your mother is $30 and the highest from your sister is $21, but the dice is the better deal.
The maximum amount you can get from your mother is $30, while the most amount you can get from your sister is $21, but the dice is the better bargain.
How to find that a given condition can be modeled by binomial distribution?Binomial distributions consist of n independent Bernoulli trials.
Bernoulli trials are those trials that end up randomly either on success (with probability p) or on failures( with probability 1- p = q (say))
Suppose we have random variable X pertaining to a binomial distribution with parameters n and p, then it is written as
\(X \sim B(n,p)\)
The probability that out of n trials, there'd be x successes is given by
\(P(X =x) = \: ^nC_xp^x(1-p)^{n-x}\)
The expected value of X is:
\(E(X) = np\\\)
You need to borrow money for gas, so you ask your mother and your sister.
You can only borrow money from one of them.
Before giving you money, they each say they will make you play a game. Your sister says she wants you to flip a fair coin.
She will give you $9 for heads and $21 for tails.
Your mother says she wants you to roll a six-sided die.
She will give you $5 times the number that appears on the die.
The expected value for a coin will be
\(E(X) = 1 \times 0.5 = 0.5\)
The expected value for a dice will be
\(E(X) = 1 \times \dfrac{1}{6} = 0.1667\)
You can easily receive $9/$21 from your sister, but it won't be as much as the dice, and you'll take a bigger risk with the dice because it has six sides.
The maximum amount you can get from your mother is $30, while the most amount you can get from your sister is $21, but the dice is the better bargain.
Learn more about binomial distribution here:
https://brainly.com/question/13609688
#SPJ2
Related Questions
Find the area of a square with side length of 4x.
Answers
Answer:
16x²
Step-by-step explanation:
since all sides of a square are equal, we just multiply 4x by 4x. this gives us 16x².
The area of square with side length 4x is 16x.
What is Square?A square is a two-dimensional closed shape with 4 equal sides and 4 vertices.
Given,
The side length of a square is 4x
We need to find the area of square.
As we know that area of square = 4a.
Where a is the length of side of a square.
In a square all the four sides will have same length.
a=4x
Area of square=4(4x)
=16x
Hence the area of square with side length 4x is 16x.
To learn more on Square click:
https://brainly.com/question/28776767
#SPJ2
(You will get brainliest if you give a long answer) You have recently purchased a new backpack as show in the picture. The main section of the backpack is made of a rectangular prism and half a cylinder. The front pocket is also a rectangular prims. Use the diagram to find the volume of your new backpack.
Explain how you calculated the answer using complete sentences and proper grammar.
Answers
*see attachment for diagram
Answer:
Volume of new backpack = 1,299.84 in.³
Step-by-step explanation:
Volume of the new back pack = volume of the front pocket + volume of the main section of the backpack
✔️Volume of the front pocket = volume of rectangular prism = L*W*H
L = 8 in.
W = 4 in.
H = 2 in.
Volume of the front pocket = 8*4*2 = 64 in.³
✔️Volume of the main section of the back pack = volume of the rectangular prism + volume of the half cylinder
= L*W*H + ½(πr²h)
L = 12 in.
W = 10 in.
H = 7 in.
r = 6 in.
h = 7 in.
Plug in the values into the equation
Volume of the main section of the backpack = 12*10*7 + ½(π*6²*7)
= 840 + ½(791.68)
= 1,235.84 in.³
✅Total volume of the new backpack = 64 + 1,235.84 = 1,299.84 in.³

66% of U.S. adults have very little confidence in newspapers. You randomly select 10 U.S. adults. Find the probability that the number of U.S. adults who have very little confidence in newspapers is (a) exactly five, (b) at least six, and (c) less than four.
Answers
Answer:
a) 0.1434 = 14.34% probability that the number of U.S. adults who have very little confidence in newspapers is exactly five.
b) 0.7731 = 77.31% probability that the number of U.S. adults who have very little confidence in newspapers is at least six.
c) 0.022 = 2.2% probability that the number of U.S. adults who have very little confidence in newspapers is less than four.
Step-by-step explanation:
For each adult, there are only two possible outcomes. Either they have very little confidence in newspapers, or they do not. Adults are independent. This means that we use the binomial probability distribution to solve this question.
Binomial probability distribution
The binomial probability is the probability of exactly x successes on n repeated trials, and X can only have two outcomes.
\(P(X = x) = C_{n,x}.p^{x}.(1-p)^{n-x}\)
In which \(C_{n,x}\) is the number of different combinations of x objects from a set of n elements, given by the following formula.
\(C_{n,x} = \frac{n!}{x!(n-x)!}\)
And p is the probability of X happening.
66% of U.S. adults have very little confidence in newspapers.
This means that \(p = 0.66\)
You randomly select 10 U.S. adults.
This means that \(n = 10\)
(a) exactly five
This is P(X = 5). So
\(P(X = x) = C_{n,x}.p^{x}.(1-p)^{n-x}\)
\(P(X = 5) = C_{10,5}.(0.66)^{5}.(0.34)^{5} = 0.1434\)
0.1434 = 14.34% probability that the number of U.S. adults who have very little confidence in newspapers is exactly five.
(b) at least six
This is:
\(P(X \geq 6) = P(X = 6) + P(X = 7) + P(X = 8) + P(X = 9) + P(X = 10)\)
So
\(P(X = x) = C_{n,x}.p^{x}.(1-p)^{n-x}\)
\(P(X = 6) = C_{10,6}.(0.66)^{6}.(0.34)^{4} = 0.232\)
\(P(X = 7) = C_{10,7}.(0.66)^{7}.(0.34)^{3} = 0.2573\)
\(P(X = 8) = C_{10,8}.(0.66)^{8}.(0.34)^{2} = 0.1873\)
\(P(X = 9) = C_{10,9}.(0.66)^{9}.(0.34)^{1} = 0.0808\)
\(P(X = 10) = C_{10,10}.(0.66)^{10}.(0.34)^{0} = 0.0157\)
\(P(X \geq 6) = P(X = 6) + P(X = 7) + P(X = 8) + P(X = 9) + P(X = 10) = 0.232 + 0.2573 + 0.1873 + 0.0808 + 0.0157 = 0.7731\)
0.7731 = 77.31% probability that the number of U.S. adults who have very little confidence in newspapers is at least six.
(c) less than four.
This is:
\(P(X < 4) = P(X = 0) + P(X = 1) + P(X = 2) + P(X = 3)\).
So
\(P(X = x) = C_{n,x}.p^{x}.(1-p)^{n-x}\)
\(P(X = 0) = C_{10,0}.(0.66)^{0}.(0.34)^{10} \approx 0\)
\(P(X = 1) = C_{10,1}.(0.66)^{1}.(0.34)^{9} = 0.0004\)
\(P(X = 2) = C_{10,2}.(0.66)^{2}.(0.34)^{8} = 0.0035\)
\(P(X = 3) = C_{10,3}.(0.66)^{3}.(0.34)^{7} = 0.0181\)
\(P(X < 4) = P(X = 0) + P(X = 1) + P(X = 2) + P(X = 3) = 0 + 0.0004 + 0.0035 + 0.0181 = 0.022\)
0.022 = 2.2% probability that the number of U.S. adults who have very little confidence in newspapers is less than four.
which one of the following is a solution to |2x-1|>3 A.2, B.-1, C.-2, D.1, E.None of these
Answers
Therefore x>2 or x<-2
—> E
-2/7 x 3/7 as fraction
Answers
Answer:
-6/49
Step-by-step explanation:
this is the answer it is very easy
Chad bought 1 box of raisins. He gave 1/6 of it to one brother, 1/4 to another brother, and he kept the rest for himself. What fraction did he keep?
Write the answer in the simplest form
Answers
Answer:
He kept 7/12 of the box.
Step-by-step explanation:
We add and convert both 1/6 and 1/4 because we cant add fractions with unlike denominators.
1/6 = 2/12 | 1/4 = 3/12
then add.
2/12 + 3/12 = 5/12.
we subtract this from a whole, which is 12/12.
12/12 - 5/12 = 7/12
he keeps 7/12 of the box
hope this helped!
You want to buy a 11-year bond with a maturity value of $12,000, and you wish to get a return of 7.25% annually. How much will you pay? (Round your answer to the nearest cent.)
Answers
Answer:The price of a bond can be calculated using the formula:
Price = Maturity Value / (1 + r)^n
Where:
Maturity Value = $12,000
r = the annual interest rate as a decimal (7.25% / 100 = 0.0725)
n = the number of years to maturity (11 years)
So the price of the bond is:
Price = $12,000 / (1 + 0.0725)^11
By solving this equation we get the price of bond is $7,065.87 approximately.
Note: The bond price is the amount you pay to buy the bond and receive the maturity value at the end of the bond term.
Step-by-step explanation:
What is (I^2)+(I^2)+3x if x=I^2?
Show your work.
Answers
Answer:
-5
Step-by-step explanation:
(i^2) = -1 so -1 -1 + 3x = 3x - 2. If x = i^2 = -1, then 3x = -3. -3 - 2 = -5
Harold adopted a St. Bernard. He
read that St. Bernards can reach up to 90 kilograms in weight. How many pounds is 90 kilograms?
Answers
Answer:
Step-by-step explanation:
The answer is 198.416
Explanation
multiply the kg value by 2.205 (rounded factor) to get pounds
What is the average rate of change for this quadratic
function for the interval from x=2 to x = 4?
A. 12
B. -6
C. -12
D. 6
-10-
Click here for long description
SUBMIT
Answers
The average rate of change of the function over the interval is -6
Finding the average rate of changeFrom the question, we have the following parameters that can be used in our computation:
The graph
The interval is given as
From x = 2 to x = 4
The function is a quadratic function
This means that it does not have a constant average rate of change
So, we have
f(2) = -3
f(4) = -15
Next, we have
Rate = (-15 + 3)/(4 - 2)
Evaluate
Rate = -6
Hence, the rate is -6
Read more about average rate of change at
brainly.com/question/17131025
#SPJ1

please helo my screenshot below

Answers
Answer:
0.0451
Step-by-step explanation:
Answer:
451/10000 or 0.0451 in decimal form
Step-by-step explanation:
Hope this helps :)
19 Five multiplied by a certain number is
added to two. The result equals four
times the number plus four.
Answers
xfgxfsdfxcxcxAnswer:
Step-by-step explanation:
Answer:
x = 2
Step-by-step explanation:
Five multiplied by a certain number is added to two
5 * x + 2
equals four times the number plus four
= 4 * x + 4
---------------------------------------------
5x + 2 = 4x + 4
Subtract 4x from both sides
x + 2 = 4
Subtract 2 from both sides
x = 2
Jillian’s school is selling tickets for a play. The tickets cost $10.50 for adults and $3.75 for students. The ticket sales for opening night totaled $2071.50. The equation 10.50 a plus 3.75 b equals 2071.50, where a is the number of adult tickets sold and b is the number of student tickets sold, can be used to find the number of adult and student tickets. If 82 students attended, how may adult tickets were sold? adult tickets
Answers
Answer:
168
Step-by-step explanation:
You are given one equation that can be used to solve this problem. The other equation you need is ...
b = 82
Using this value in the given equation, you can find "a".
10.50a +3.75b = 2071.50 . . . . . . . given
10.50a +3.75·82 = 2071.50 . . . . . .using 82 for b
10.50a +307.50 = 2071.50 . . . . . . evaluated
10.50a = 1764 . . . . . . . subtract 307.50
a = 168 . . . . . . . . . . . . . divide by 10.50
168 adult tickets were sold.
Answer:
168 Adult tickets were sold
Step-by-step explanation:
Make me brainliest
PLEASE HELP ASAP THIS IS FOR ALGEBRA PLEASE EXPLAIN AS WELL
5. What is the next term of the sequence -3, 6, -12, 24,…?
Answers
Answer:
-48
Step-by-step explanation:
we can see each number is getting doubled but flipped from negative and positive and vise versa. aka getting multiple by negative 2
we can also double check our work by multiplying each number in the sequence we have by -2 and make sure it follows the sequence.
At the neighborhood block party, Joel served 1/6 of a gallon of hot chocolate and 1/12 of a
gallon of apple cider. How much more hot chocolate than apple cider did Joel serve?
Write your answer as a fraction or as a whole or mixed number.
gallons
Answers
Answer:
1/12 gallons
Step-by-step explanation:
We can determine how much more hot chocolate than apple cider die Joe serve by subtracting 1/12 from 1/6.
Step 1: Since 1/12 has the bigger denominator and 6 * 2 = 12, let's give 1/6 the same denominator as 1/12 by multiplying the entire fraction by 2/2
(1/6) * (2/2) = 2/12
Step 2: Now we can subtract 1/12 from 2/12:
2/12 - 1/12 = 1/12
Thus, Joel served 1/12 more gallons of hot chocolate than apple cider.
let g(x)=-x^2+8x+4. find g(-5)
Answers
Answer:
-11
Step-by-step explanation:
g(-5)=-5^2+8(-5) +4
=25+-40+4
=-11
HELP 10 MIN LEFT!!!!

Answers
Answer:
To one decimal place,
y = 16.3 m
Step-by-step explanation:
Using SOHCAHTOA,
In this case we need to use CAH,
WE know the angle = 25 and the hypotenuse H = 18,
so,
y = adjacent
\(cos(angle) = y/H\\y = (18)(cos(25))\\y = 16.3135\\y = 16.3\)
Answer: 16.3 in.
Step-by-step explanation:
use SOH CAH TOA
cos x = adj/hyp
cos 25 = y/18
18 cos 25 = y
y= 16.3
A positive real number is 1 less than another. When 2 times the larger is added to the square of the smaller, the result is 8. Find the numbers.
Answers
Answer:
Let your two numbers be n and n-1. Then: 2n+n²-2n+1=51 n²=50 n=5√2 n-1=5√2-1
Hope that helps <3
What is the result if the product of 5 and 75 is divided by 3?
Answers
Answer: 125
Step-by-step explanation: product of 5 and 75 = 5*75 = 375 divided by 3 which is 375/3 = 125.
distribute to simplify -0.8(-27 - 15u)
Answers
Find the slope from the table.

Answers
Answer:
m=0
Step-by-step explanation:
the slope is calculated using two points on the line and the formula
m = (y2 - y1) ÷ (x2 - x1)
where
x1 and y1 are the coordinates of point 1
x2 and y2 are the coordinates of point 2
for example, you can take
point 1 = (x1;y1) = (-2;3)
point 2 = (x2;y2) = (-1;3)
then your slope is
m = (3 - 3) ÷ (-1 - (-2)) = 0
notice that x1 is always at the left of x2 on the x axis
and it makes sense that your slope is 0 because for each x your y is the same
In a class of 20 kindergarteners, 10 are wearing blue shirts, 5 are wearing green shirts, and 5 are wearing red shirts. A group of 10 kindergarteners is chosen at random to go outside for play time. What is the probability that exactly two of the group are wearing red shirts
Answers
as there are 30 children and from 30 children 2 will be picked (which will than be 2/30)
but if we simplify that by 2, than that will lead to the ANSWER OF: 1/15
A pipe has a diameter of 2.5 inches. Insulation that is 0.5 inch thick is placed around the pipe. What is the diameter of the pipe with the insulation around it?
Answers
Answer:
So the diameter of the pipe with the insulation around it is approximately 18.84 inches / 2 = 9.42 inches.
Step-by-step explanation:
To find the diameter of the pipe with the insulation around it, we can use the formula for the circumference of a circle:
C = 2 * π * r
Where:
· C = circumference of the pipe
· π = the mathematical constant approximately equal to 3.14
· r = the radius of the pipe
Using the given information, we know that the pipe’s diameter is 2.5 inches and that the insulation around the pipe is 0.5 inch thick. Therefore, the radius of the pipe with the insulation around it is:
r = 2.5 inches + 0.5 inch = 3 inches
Plugging in the values:
C = 2 * π * 3
C = 6.28 * 3
C = 18.84 inches
Note that this is only an approximation, as the thickness of the insulation is slightly larger than the diameter of the pipe. To obtain a more accurate result, we would need to use a geometric area formula or a numerical integration technique.
The sum of two numbers is 144 and their difference is 73. Find the smallest number. Use two exact decimals.
Answers
Answer:
30.5
Step-by-step explanation:
Let L = the larger number
Let S = the smaller number
L + S = 144
L - S = 73
L = S + 73
S + S + 73 = 144
2S = 71
S = 30.5
This graph shows a proportional relationship.
What is the constant of proportionality?
Answers
The constant of proportionality is a crucial aspect of a proportional relationship, as it tells us how much one variable changes in relation to the other. It can be calculated from the equation of the relationship, or from the slope of the graph if it is a linear relationship.
A proportional relationship is a mathematical equation that expresses two variables that are in proportion to one another. In this type of relationship, if one variable is multiplied by a certain constant factor, then the other variable will be multiplied by the same constant factor. For example, if the cost of 3 books is $15, then the cost of 6 books will be $30. In this case, the number of books and the cost of the books are in proportion to one another.
The constant of proportionality is the constant factor by which the two variables are multiplied to obtain each other. In other words, it is the ratio between the two variables that remain constant in a proportional relationship. It can be represented by the letter k, and is calculated by dividing one variable by the other.
To find the constant of proportionality from a graph, we need to look at the slope of the line. The slope is the ratio between the change in the y-values and the change in the x-values, which is also known as the rise over run. If the graph shows a proportional relationship, then the slope will remain constant throughout the graph.
For example, if the graph shows the relationship between the number of hours worked and the amount of money earned, and the slope is 10, then the constant of proportionality is 10. This means that for every hour worked, the person earns $10. The equation for this proportional relationship can be written as y = 10x, where y represents the amount of money earned and x represents the number of hours worked.
In conclusion, the constant of proportionality is a crucial aspect of a proportional relationship, as it tells us how much one variable changes in relation to the other. It can be calculated from the equation of the relationship, or from the slope of the graph if it is a linear relationship.
For more such questions on constant of proportionality, click on:
https://brainly.com/question/1835116
#SPJ8
How many different 3-digit numbers can you write if you may use only the digits 2, 5 and 7, each of them no more than once?
Answers
Answer:
dream is cool................
PLEASE HELP
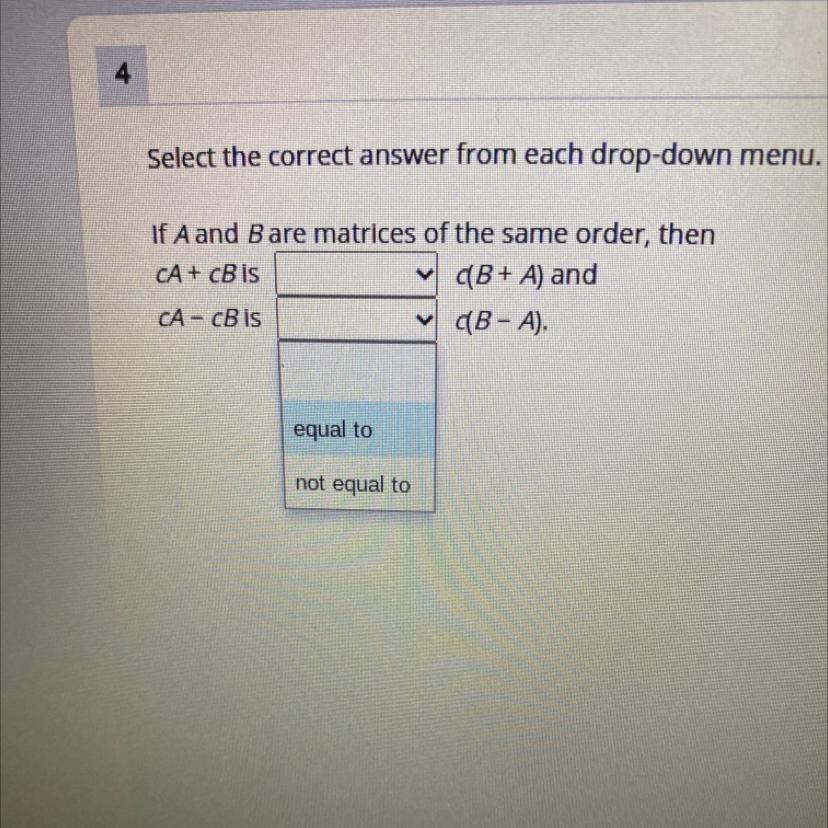
Select the correct answer from each drop-down menu. Options are (equal to, not equal to)
Answers
Answer:
Not equal to.
Step-by-step explanation:
A jar contains 20 yellow jellybeans, 20 orange jellybeans, 20 red jellybeans and 20 green jellybeans.
Required:
a. In how many ways can you put all the jellybeans in a row?
b. How many ways are there to select a handful of 20 jellybeans?
c. How many ways are there to select a handful of 20 jellybeans that contains at least 3 red?
d. How many ways are there to select a handful of 20 jellybeans that contains at least 3 red and at most 2 orange?
Answers
Answer:
A)
\(\left \{ {{80} \atop {20}} \} * \left \{ {{60} \atop {20}} \} * \left \{ {{40} \atop {20}} \} * \left \{ {{20} \atop {20}} \}\)
B)
\(\left \{ {{20+4-1} \atop {4-1}} \} = \left \{ {{23} \atop {3}} \}\)
C)
= \(\left \{ {{17+4+1} \atop {4-1}} \} = \left \{ {{20} \atop {3}} \}\)
D)
= \(\left \{ {{20} \atop {3}} \} - \left \{ {{17} \atop {3}} \}\)
Step-by-step explanation:
A) How many ways can you put all Jellybeans in a row
Total number of Jellybeans = 80
The first jellybeans = 20 yellow , second is 20 orange jellybeans , third is 20 red jellybeans , fourth is 20 green jellybeans
Therefore the number of ways the Jellybeans can be put in a row is :
\(\left \{ {{80} \atop {20}} \} * \left \{ {{60} \atop {20}} \} * \left \{ {{40} \atop {20}} \} * \left \{ {{20} \atop {20}} \}\)
B) How many ways are there to select a handful of 20 jellybeans
lets assume:
yellow jellybeans = a , orange jellybeans = b , red jellybeans = c , green jellybeans = d
a + b + c + d = 20
This is the number Non-negative integer solutions
= \(\left \{ {{20+4-1} \atop {4-1}} \} = \left \{ {{23} \atop {3}} \}\)
C) This is also the number of Non-negative integer solutions but in this case the value of C ≥ 3
hence the number of ways to select a handful of 20 jellybeans that contains at least 3 red
= \(\left \{ {{17+4+1} \atop {4-1}} \} = \left \{ {{20} \atop {3}} \}\)
D) In this case the value of C ≥ 3 and B ≤ 2
Hence the number of ways to select a handful of 20 jellybeans that contains at least 3 red and at most 2 orange
= \(\left \{ {{20} \atop {3}} \} - \left \{ {{17} \atop {3}} \}\)
Need help with this....

Answers
Answer:
Step-by-step explanation:
try substituting the points into both of the equations like it's a slope equation.
In a biomedical research study, it was determined that the survival time, in weeks, of an animal subjected to a certain exposure of gamma radiation has a gamma distribution with α= 5 and β=10.
a. What is the mean survival time of a randomly selected animal of the type used in the experiment?
b. What is the standard deviation of survival time?
c. What is the probability that an animal survives more than 30 weeks?
Answers
Answer:
Step-by-step explanation:
From the given information:
Let X be the random variable;
The mean survival time is E(X):
E(X) = μ
E(X) = ∝β
E(X) = 5 × 10
E(X) = 50
To find the standard deviation, we must first determine the variance:
\(V(X) = \sigma ^2\)
\(V(X) = \alpha \beta ^2\)
\(V(X) = 5 \times (10)^2\)
\(V(X) = 5 \times 100\)
\(V(X) = 500\)
The standard deviation is:
\(\sigma =\sqrt{V(X)}\)
\(\sigma =\sqrt{500}\)
\(\sigma =22.361\)
The standard deviation of survival time = 22.361
(c)
P(X>30) = 1 - P(X ≤ 30)
\(= 1 - \int \limits ^{30}_{0} \ f(x) \ dx\)
\(= 1 - \int \limits ^{30}_{0} \dfrac{1}{\beta^{\alpha} \Gamma \alpha }x^{a-1} e ^{-x/\beta } \ dx\)
\(= 1 - \int \limits ^{30}_{0} \dfrac{1}{\beta^{\alpha} \Gamma (5)}x^{5-1} e ^{-x/10 } \ dx --- (1)\)
So, if:
\(y = \dfrac{x}{10}\)
\(dy = \dfrac{dx}{10}\)
10dy = dx
and limits of y are 0 and 3.
because;
for x = 0
\(y = \dfrac{0}{\beta}\)
y = 0
For x = 30
\(y = \dfrac{30}{10}\)
y = 10
From (1);
\(P(X> 30) = 1 - \int \limits ^{30}_{0} \dfrac{1}{\beta^{\alpha} \Gamma (5)}x^{5-1} e ^{-x/10 } \ dx\)
\(P(X> 30) = 1 - \int \limits ^{3}_{0} \dfrac{(10y)^4}{10^{5} \Gamma (5)}e ^{-y } \ dy\) since y = x/β
\(P(X> 30) = 1 - \int \limits ^{3}_{0} \dfrac{10^4 y^4 \ e^{-y} }{10^{4} \Gamma (5)} \ dy\)
\(P(X> 30) = 1 - \int \limits ^{3}_{0} \dfrac{y^4 \ e^{-y} }{ \Gamma (5)} \ dy\)
Since;
\(F(a, \alpha )= \int \limits ^a_0 \dfrac{y^{a-1}e^{-y}}{\Gamma (\alpha )} dy\)
Then;
P(X> 30) = 1 - F(3,5)
From the table of incomplete gamma function;
P(X > 30) = 1 - 0.185
P(X > 30) = 0.815
Thus, the probability that an animal survives more than 30 weeks is 0.815
a)The mean survival time of a randomly selected animal of the type used in the experiment is 50.
b)Standard deviation of survival time is 22.36
What is the standard deviation?The standard deviation of a random variable, sample, statistical population, data set, or probability distribution is the square root of its variance.
Suppose x is the random variable.
It is given that α= 5 and β=10.
So, the mean survival E(x)=α β
The mean survival E(x) =5*10
The mean survival E(x) =50
We know that Variance =α β²
So, Variance = 5*10²
Variance =500
We know that standard deviation σ = √Variance
σ = √500
σ = 22.36
Therefore, a)the mean survival time of a randomly selected animal of the type used in the experiment is 50.
b)Standard deviation of survival time is 22.36
To get more about standard deviation visit:
https://brainly.com/question/475676
The standard deviation is:
The standard deviation of survival time = 22.361