You drive a car that holds 15 gallons of gasoline. Your car uses 0.03 gal per mile. Which equation best represents this information

Answers
Related Questions
Through: (-1,-2), slope=-5/2

Answers
now, assuming it's asking for its equation.
\((\stackrel{x_1}{-1}~,~\stackrel{y_1}{-2})\hspace{10em} \stackrel{slope}{m} ~=~ - \cfrac{5}{2} \\\\\\ \begin{array}{|c|ll} \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-\stackrel{y_1}{(-2)}=\stackrel{m}{- \cfrac{5}{2}}(x-\stackrel{x_1}{(-1)}) \implies y +2 = - \cfrac{5}{2} ( x +1) \\\\\\ y+2=- \cfrac{5}{2}x-\cfrac{5}{2}\implies y=- \cfrac{5}{2}x- \cfrac{5}{2}-2\implies {\Large \begin{array}{llll} y=- \cfrac{5}{2}x- \cfrac{9}{2} \end{array}}\)
I NEED AN ANSWER ASAP PLEASE

Answers
Step-by-step explanation:
the correct answer is option a 6a-7
What is the approximate length of the track in miles

Answers
Explanation
Opposite sides are 5 miles each and for each semicircle we have:
\(\frac{2\pi *\frac{1}{2}}{2}=\frac{\pi}{2}\text{ miles}\)Then the lenght of the track is:
\(5+5+\frac{\pi}{2}+\frac{\pi}{2}=10+\pi\)Approximately 13.1416 miles
how many acres are in a piece of property measuring 620' x 430'?
Answers
There will be 6.11 acres in a piece of property measuring 620' x 430'
To calculate the number of acres in a piece of property, you need to convert the measurements from feet to acres.
1 acre is equal to 43,560 square feet.
Given that the property measures 620' x 430', you can calculate the area in square feet by multiplying the length by the width: 620' x 430' = 266,600 square feet.
To convert the area from square feet to acres, divide the square footage by 43,560: 266,600 square feet / 43,560 = 6.11 acres (rounded to two decimal places).
Therefore, the piece of property measures approximately 6.11 acres.
Learn more about acres at https://brainly.com/question/32041761
#SPJ11
you roll a 6 sided die.
What is P(not greater than 3)? Write your answer as a fraction or whole number.
Answers
Answer:
1/2
Step-by-step explanation:
options in a 6 sided die= 1,2,3,4,5,6
greater than 3 = 4,5,6
so three sides out of a 6 sided die is greater than three
P(not greater than 3) = \(\frac{6-3}{6} = \frac{1}{2}\)
Answer:
1/2 or 0.5
Step-by-step explanation:
The probability of rolling a number greater than 3 on a six-sided die is 3/6 or 1/2, since there are three numbers (4, 5, 6) out of six that are greater than 3.
To find the probability of not rolling a number greater than 3, we can subtract the probability of rolling a number greater than 3 from 1:
P(not greater than 3) = 1 - P(greater than 3)
P(not greater than 3) = 1 - 1/2
P(not greater than 3) = 1/2
Therefore, the probability of not rolling a number greater than 3 is 1/2 or 0.5.
write the integral as the sum of the integral of an odd function and the integral of an even function.
Answers
We can write the integral of f(x) as the sum of the integral of the even component, e(x), and the integral of the odd component, o(x). This gives us the following equation: ∫f(x)dx = ∫e(x)dx + ∫o(x)dx
Integrals can be written as the sum of the integral of an odd function and the integral of an even function. This is because any function can be broken down into its even and odd components. Even functions are those that remain unchanged when reflected over the x-axis. This means that the result of evaluating the function for any x-value is the same as the result for its negative. Odd functions are those that change sign when reflected over the x-axis. This means that the result of evaluating the function for any x-value is the negative of the result for its negative.
The integral of an even function is the same regardless of whether it is written as the sum of the integral of an odd function and the integral of an even function, or if it is written just as an integral of the even function. The integral of an odd function is the negative of the integral of the even function when written as the sum of the two integrals.
To know more about functions click here:
https://brainly.com/question/29769447
#SPJ11
The bonus question asks for the application of the integral test to determine the convergence of the series given by 2n*e^(-a).
The integral test is a method used to determine the convergence or divergence of a series by comparing it to the integral of a related function. In this case, we are given the series 2n*e^(-a), and we can use the integral test because the terms of the series involve the variable 'n', and the function e^(-a) can be integrated.
To apply the integral test, we consider the integral of the function corresponding to the series. In this case, we integrate the function f(x) = 2x*e^(-a) from 1 to infinity. If this integral converges, then the series is also convergent. Conversely, if the integral diverges, then the series is divergent.
By evaluating the integral of f(x) and analyzing its convergence or divergence, we can determine whether the given series 2n*e^(-a) converges or diverges. Showing all the steps in evaluating the integral and discussing the convergence properties of the resulting integral will be necessary to receive full credit for this question.
Learn more about integral:
https://brainly.com/question/31109342
#SPJ11
I need help with this, please and thank you to anyone who can do this.

Answers
Answer:
No
Step-by-step explanation:
Sooooooooooooo no
P.S. The answer is accually (Deleted)
Answer:
it is not correct
Step-by-step explanation:
the answer is instead of 55 its 73
if this is wrong im sryyyyy
A baseball team plays in a stadium that holds 70000 spectators. With the ticket price at $11 the average attendence has been 28000. When the price dropped to $8, the average attendence rose to 35000. Assume that attendence is linearly related to ticket price.
What ticket price would maximize revenue?
Answers
The ticket price that would maximize revenue for the baseball team is $10.
To determine the ticket price that maximizes revenue, we need to find the point where the product of the ticket price and attendance is highest. In this case, we have two data points: when the ticket price is $11, the average attendance is 28,000, and when the ticket price is $8, the average attendance is 35,000.
We can start by calculating the revenue at each data point. Revenue is calculated by multiplying the ticket price by the attendance. At $11 per ticket, the revenue is $11 * 28,000 = $308,000. At $8 per ticket, the revenue is $8 * 35,000 = $280,000.
By comparing the revenues at these two data points, we can see that the revenue is higher when the ticket price is $11. However, this is not the ticket price that maximizes revenue. To find the optimal ticket price, we need to determine the point where the revenue is highest.
Since attendance is linearly related to the ticket price, we can assume a linear equation of the form y = mx + b, where y represents attendance, x represents ticket price, m represents the slope of the line, and b represents the y-intercept. Using the two data points, we can calculate the slope:
m = (35,000 - 28,000) / ($8 - $11) = 7,000 / (-$3) = -2,333.33
Now, we can substitute the slope and one of the data points into the equation to calculate the y-intercept (b):
28,000 = -2,333.33 * $11 + b
b = 28,000 + $25,666.63 = $53,666.63
With the equation y = -2,333.33x + $53,666.63, we can find the attendance at any given ticket price. To maximize revenue, we need to find the ticket price that corresponds to the maximum point of the revenue curve.
Revenue = Ticket Price * Attendance
Revenue = x * (-2,333.33x + $53,666.63)
Revenue = -2,333.33x^2 + $53,666.63x
To find the ticket price that maximizes revenue, we can use calculus. By taking the derivative of the revenue function with respect to x and setting it equal to zero, we can find the critical point:
dRevenue/dx = -4,666.66x + $53,666.63 = 0
4,666.66x = $53,666.63
x = $53,666.63 / 4,666.66 ≈ $11.50
However, since the ticket price must be a multiple of $0.50, the closest valid ticket price is $11. Therefore, the ticket price that would maximize revenue for the baseball team is $10.
Learn more about: Revenue
brainly.com/question/29061057
#SPJ11
42. Find the equation of the sphere with center C(−2,3,7) that is tangent to the plane 2x+3y−6z=5.
Answers
To find the equation of the sphere tangent to the plane 2x + 3y - 6z = 5 with center C(-2, 3, 7), we need to find the radius of the sphere. The equation of the sphere is (x + 2)^2 + (y - 3)^2 + (z - 7)^2 = 36.
The distance from the center of the sphere to the plane is equal to the radius. We can use the formula for the distance between a point (x, y, z) and a plane Ax + By + Cz + D = 0:
Distance = |Ax + By + Cz + D| / sqrt(A^2 + B^2 + C^2)
In this case, the plane equation is 2x + 3y - 6z - 5 = 0. Plugging in the coordinates of the center C(-2, 3, 7) into the formula, we have:
Distance = |2(-2) + 3(3) - 6(7) - 5| / sqrt(2^2 + 3^2 + (-6)^2)
= |-4 + 9 - 42 - 5| / sqrt(4 + 9 + 36)
= |-42| / sqrt(49)
= 42 / 7
= 6
So, the radius of the sphere is 6.
The equation of a sphere with center C(-2, 3, 7) and radius 6 is:
(x + 2)^2 + (y - 3)^2 + (z - 7)^2 = 6^2
Simplifying further, we have:
(x + 2)^2 + (y - 3)^2 + (z - 7)^2 = 36
Therefore, the equation of the sphere is (x + 2)^2 + (y - 3)^2 + (z - 7)^2 = 36.
Learn more about radius here
https://brainly.com/question/24375372
#SPJ11
Three of the following representations match while one does not. Which one is incorrect? How could the student correct it? DESCRIPTION EQUATION At Sherri's Sundae Shop, customers pay $4 for a bowl of ice cream plus $0.20 per topping. y = .25x + 4 SHERRI'S SUNDAE SHOP TOPPINGS TOTAL COST (S) 1425 2 $4.50 TOTAL COST (S) 3 $4.75 4 $5.00 5 15.25 $5.50 TOPPINGS TABLE GRAPH

Answers
Answer:
Description
Step-by-step explanation:
.20(8)+4=5.6
on the graph the point is (8,6)
.25(8)+4=6
Here is an equation that is true for all values of x: 6(x + 3) = 6x + 18. Londyn saw this equation and says she can tell 18( x + 3) + 32 = 3(6x + 18) + 32 is also true for any value of x. How can she tell? Explain your reasoning.

Answers
We need to decide whether the given equations are always or never true for values of x .The given equations are ,
\(x - 12 = x + 1\)solve out for x,
\(\longrightarrow x -x =12+1\\ \)
\(\longrightarrow 0 =13\\ \)
This can never be true. Hence the equation is never true for any values of x.
\(x + \frac{3}{4} = x - \frac{3}{4} \)solve out for x,
\(\longrightarrow x -x =\dfrac{3}{4}+\dfrac{3}{4}\\ \)
\(\longrightarrow 0=\dfrac{3}{2}\)
This can never be true. hence the equation is never true for any values of x.
\(4(x + 3) = 8x + 12 - 4x\)solve out for x,
\(\longrightarrow 4x +12=8x+12-4x\\\)
\(\longrightarrow 4x -8x +4x =12-12\\\)
\(\longrightarrow 0=0\)
hence this equation is true for all values of x.
\(2x - 8 - x = x - 8\)solve out for x,
\(\longrightarrow 2x -x -x =8+8\\ \)
\(\longrightarrow 0=0 \)
hence the equation is true for all values of x.
\(2(x + 5) + 3x = 5(x - 5)\)solve out for x,
\(\longrightarrow 2x +10+3x =5x-25\\ \)
\(\longrightarrow 5x -5x =-25-10\\\)
\(\longrightarrow 0 =-35\)
This can never be true. hence the equation is never true for any values of x.
and we are done!
For the linear regression y = ẞ1 + ẞ2x + e, assuming that the sum of squared errors (SSE) takes the following form:
SSE = 382 +681 +382 + 18ẞ1ẞ2
Derive the partial derivatives of SSE with respect to B1 and B2 and solve the optimal values of these parameters.
a. B₁ = B1
b. B₂ =
Answers
The optimal values of these parameters are:
a. β₁ = 0
b. β₂ = 0
The linear regression y = β1 + β2x + e, assuming that the sum of squared errors (SSE) takes the following form:
SSE = 382 + 681 + 382 + 18β1β2
Derive the partial derivatives of SSE with respect to β1 and β2 and solve the optimal values of these parameters.
Given that SSE = 382 + 681 + 382 + 18β1β2 ∂SSE/∂β1 = 0 ∂SSE/∂β2 = 0
Now, we need to find the partial derivative of SSE with respect to β1.
∂SSE/∂β1 = 0 + 0 + 0 + 18β2 ⇒ 18β2 = 0 ⇒ β2 = 0
Therefore, we obtain the optimal value of β2 as 0.
Now, we need to find the partial derivative of SSE with respect to β2. ∂SSE/∂β2 = 0 + 0 + 0 + 18β1 ⇒ 18β1 = 0 ⇒ β1 = 0
Therefore, we obtain the optimal value of β1 as 0. Hence, the partial derivative of SSE with respect to β1 is 18β2 and the partial derivative of SSE with respect to β2 is 18β1.
Thus, the optimal values of β1 and β2 are 0 and 0, respectively.
Therefore, the answers are: a. β₁ = 0 b. β₂ = 0
Learn more about regression analysis at
https://brainly.com/question/31691955
#SPJ11
What is 3x+12 = 10x-15
Answers
Answer: 3.85714285714=x
Step-by-step explanation:
3x+12=10x-15
-3x -3x
12=7x-15
+15 +15
27=7x
27/7=7x/7
3.85714285714=x
:)
An online music store is offering a promotion. When you spend $45 or more, you receive 3 songs for free. You buy an album for $15. Identify the inequality that represents how much more money m you must spend to receive the three free songs.
Answers
Answer: x ≥ $30.
Where x is the amount of money that you need to spend if you want to have the 3 free songs.
Step-by-step explanation:
When you spend $45 or more, you get 3 free songs.
You already bought an album that costs $15, then the minimum amount that you need to spend is (when you spend exactly $45):
$45 - $15 = x = $30.
Then the inequality is:
x ≥ $30.
Because if you spend more than $45 you also get the songs.
Identify the surface with the given vector equation. r(s, t) = (s cos(t), s sin(t), s) circular paraboloid O elliptic cone O hyperbolic paraboloid O plane O circular cone X
Answers
The surface with the given vector equation, r(s, t) = (s cos(t), s sin(t), s), is a circular cone.
The vector equation r(s, t) = (s cos(t), s sin(t), s) represents a surface in three-dimensional space. Let's analyze the equation to determine the nature of the surface.
In the equation, we have three components: s, cos(t), and sin(t). The presence of s indicates that the surface expands or contracts radially from a central point. The trigonometric functions cos(t) and sin(t) determine the angle at which the surface extends in the x and y directions.
By observing the equation closely, we can see that as s increases, the radius of the surface expands uniformly in all directions, while the height remains constant. This behavior is characteristic of a circular cone. The circular base of the cone is defined by s cos(t) and s sin(t), and the vertical component is determined by s.
Therefore, the surface described by the vector equation r(s, t) = (s cos(t), s sin(t), s) is a circular cone.
Learn more about vector equation here :
https://brainly.com/question/32619742
#SPJ11
Calculate (1.11) and (8.2)
Answers
Answer:
9.102
Step-by-step explanation:
Assuming this means multiply to each other
1.11 x 8.2 = 9.102
Guessing this it multiplication
1.11 • 8.2 = 9.102
Ten percent of the items produced by a machine (ongoing process) are defective. A random sample of 100 items is selected and checked for defects. What is the probability that the sample will contain more than 5% defective units
Answers
The probability that the sample will contain more than 5% defective units is approximately 0.9525 or 95.25%.
To solve this problem, we can use the binomial distribution formula:
P(X > 5) = 1 - P(X ≤ 5)
where X is the number of defective items in a sample of size n = 100, and p = 0.1 is the probability of an item being defective.
To calculate P(X ≤ 5), we can use the binomial cumulative distribution function (CDF) or a binomial probability table. Alternatively, we can use a normal approximation to the binomial distribution, which is valid when np ≥ 10 and n(1-p) ≥ 10, as is the case here (np = 10 and n(1-p) = 90).
Using the normal approximation, we can standardize the distribution of X as follows:
\(z = (X - np) / \sqrt{(np(1-p))}\)
Then, we can use a standard normal table or calculator to find the probability of z ≤ z0, where z0 is the standardized value corresponding to X = 5.
Let's use the normal approximation method to solve the problem:
np = 100 x 0.1 = 10
σ = \(\sqrt{(np(1-p))} = \sqrt{(9)} = 3\)
z0 = (5 - 10) / 3 = -1.67 (rounded to two decimal places)
Using a standard normal table or calculator, we find that P(Z ≤ -1.67) = 0.0475 (rounded to four decimal places).
Therefore, P(X > 5) = 1 - P(X ≤ 5) = 1 - 0.0475 = 0.9525 (rounded to four decimal places).
for such more question on probability
https://brainly.com/question/13604758
#SPJ11
(car sales) of the cars sold during the month of july, 87 had air conditioning, 99 had automatic transmission, and 73 had power steering. 8 cars had all three of these extras. 24 cars had none of these extras. 24 cars had only air conditioning, 64 cars had only automatic transmissions, and 35 cars had only power steering. 9 cars had both automatic transmission and power steering. how many cars had exactly two of the given options?
Answers
Cars with exactly two options = Total cars - Cars with none or one option - Cars with all three options. 8 cars had exactly two of the given options during the month of July.
To determine the number of cars that had exactly two of the given options (air conditioning, automatic transmission, and power steering), we can follow these steps:
1. Find the total number of cars sold in July.
2. Subtract the number of cars with none, one, or all three options to get the number of cars with exactly two options.
Step 1: Find the total number of cars sold in July
- 24 cars had none of the extras
- 24 cars had only air conditioning
- 64 cars had only automatic transmission
- 35 cars had only power steering
- 8 cars had all three extras
Total cars = 24 + 24 + 64 + 35 + 8 = 155 cars
Step 2: Subtract the number of cars with one or all three options
- 87 cars had air conditioning
- 99 cars had an automatic transmission
- 73 cars had power steering
- 8 cars had all three extras
Total cars with at least one option = 87 + 99 + 73 - 8 = 251 cars
Now, subtract the number of cars with none or one option from the total number of cars to find the number of cars with exactly two options:
Cars with exactly two options = Total cars - Cars with none or one option - Cars with all three options
Cars with exactly two options = 155 - (24 + 24 + 64 + 35) - 8 = 155 - 147 = 8 cars
Therefore, 8 cars had exactly two of the given options during the month of July.
Learn more about Month:
brainly.com/question/1248107
#SPJ11
Help me please and thank you! try your best i will mark brainlist who is first and accurate.

Answers
Answer:
the first
Step-by-step explanation:
if it's perpendicular so is the gradient so y= -5/6 + 12
*I'm so sorry if I'm wrong
Solve each equation 8x+11=2(4x-7)+25
Answers
Answer:
Any value of x makes the equation true.
All real numbers
Interval Notation:
(−∞,∞)
Step-by-step explanation:
Answer:
x=0
Step-by-step explanation:
8x+11=2(4x-7)+25
8x+11=8x-14+25
8x+11=8x+11
8x-8x=11-11
x=0
Use the associative property to simplify the expression.
43 +30+70
OA. 43+30+70 = 73 +70 = 143
OB. 43+ (30+70) = 43+ 100 = 143
OC. 43+ 10(3 + 7) = 43 + 10(10) = 143
OD. 43 +70+ 30 = 113 +30 = 143
SUBMIT
Answers
Answer:jjj
Step-by-step explanation:because
What are the other types of coordinate systems? What information is necessary to define points within each system?
Answers
The quotient of a number, 2, and 21 is 42.
Which equation and value of & represent this relationship?
Answers
The equation will be written as (42/2) = 21.
What is an expression?The mathematical expression combines numerical variables and operations denoted by addition, subtraction, multiplication, and division signs.
Mathematical symbols can be used to represent numbers (constants), variables, operations, functions, brackets, punctuation, and grouping. They can also denote the logical syntax's operation order and other properties.
Given that the quotient of a number, 2, and 21 is 42. The equation of the quotient will be written as,
42 / 2 = 21
Here the value 42 when divided by 2 will give 21.
Therefore, the equation will be written as (42/2) = 21.
To know more about an expression follow
https://brainly.com/question/28416731
#SPJ1
evaluate the double integral. 8y2 da, d is the triangular region with vertices (0, 1), (1, 2), (4, 1) d
Answers
The value of the double integral is 128/27 - 32/9 + 8ln2/3. From triangular region with vertices (0, 1), (1, 2), (4, 1) d.
To evaluate the double integral, we first need to set up the limits of integration. Since the region D is a triangle, we can use the following limits:
0 ≤ x ≤ 1
1 + x ≤ y ≤ 4 - x
The integral then becomes:
∫0^1 ∫1+x^4-x 8y^2 dy dx
Evaluating the integral with respect to y first, we get:
∫0^1 ∫1+x^4-x 8y^2 dy dx = ∫0^1 [(8/3)(y^3)]1+x^4-x dx
= ∫0^1 [(8/3)(1+x^3)^3 - (8/3)(1+x^2)^3] dx
= 128/27 - 32/9 + 8ln2/3
Learn more about integral: https://brainly.com/question/27419605
#SPJ11
Ammonia is synthesized in the Haber Process following the reaction N2(g) + H2(g) -> NH3(g). In the reactor, a limiting reactant conversion of 20.28% is obtained when the feed contains 72.47% H2, 15.81% N2, and the balance being argon (inert). Determine the amount of hydrogen in the product stream.
Type your answer as a mole percent, 2 decimal places.
Answers
The mole percent of hydrogen in the product stream is 84.25%.
Solution:Calculate the number of moles of each component in the feed:
For 100 g of the feed,
Mass of H2 = 72.47 g
Mass of N2 = 15.81 g
Mass of argon = 100 - 72.47 - 15.81 = 11.72 g
Molar mass of H2 = 2 g/mol
Molar mass of N2 = 28 g/mol
Molar mass of argon = 40 g/mol
Number of moles of H2 = 72.47/2 = 36.235
Number of moles of N2 = 15.81/28 = 0.5646
Number of moles of argon = 11.72/40 = 0.293
Number of moles of reactants = 36.235 + 0.5646 = 36.7996
From the balanced chemical equation: 1 mole of N2 reacts with 3 moles of H21 mole of N2 reacts with 3/0.5646 = 5.312 moles of H2
For 0.5646 moles of N2,
Number of moles of H2 required = 0.5646 × 5.312 = 3.0005 moles
∴ Hydrogen is in excess
Hence, the number of moles of ammonia formed = 20.28% of 0.5646 = 0.1144 moles
Number of moles of hydrogen in the product stream = 3.0005 moles (unchanged)
Amount of nitrogen in the product stream = 0.5646 - 0.1144 = 0.4502 moles
Total number of moles in the product stream = 3.0005 + 0.1144 + 0.4502
= 3.5651 mol
Mole fraction of H2 in the product stream: XH2 = 3.0005/3.5651
= 0.8425Mole percent of H2 in the product stream: 84.25%
Therefore, the mole percent of hydrogen in the product stream is 84.25%.
Know more about hydrogen here:
https://brainly.com/question/24433860
#SPJ11
Sami earns £4.50 per hour. How many hours does he need to work to earn £90?
Answers
Answer:
20 hours hope this helps :)
Step-by-step explanation:
Answer:
20 hours :)
Step-by-step explanation:
Sami earns 4.50 per hour and needed 90.00. What I did was I divided 90 by 4.5 to find out how many hours he would need to work.
90/4.5=20
ps can u please give me brainly
A net force of 125 N is applied to a certain object. As a result, the object accelerates with an acceleration of 24.0 m/s2. The mass of the object is 144 kg.
Answers
The net force acting on the object is 3456 N, the objective with an acceleration.
The net force applied to an object is equal to the product of its mass and acceleration, according to Newton's second law of motion. Mathematically, this can be represented as:
Fnet = ma
Where Fnet is the net force, m is the mass, and a is the acceleration. In your scenario, the net force applied to the object is 125 N, and its acceleration is 24.0 m/s2. Therefore, we can rearrange the formula and solve for the mass of the object as follows:
m = Fnet / a
m = 125 N / 24.0 m/s2
m = 5.21 kg
However, this answer does not match the given mass of the object, which is 144 kg. This suggests that there may be an error in one of the values provided. Assuming the mass of the object is actually 144 kg, we can use the same formula to solve for the net force acting on it as follows:
Fnet = ma
Fnet = 144 kg * 24.0 m/s2
Fnet = 3456 N
To know more about net force:
https://brainly.com/question/29971999
#SPJ11
The mass of an object with net force value = 125 Newton and acceleration of 24.0 m/s² is equals to the 5.208 kg. So, option(c) is right one.
The force formula is derived by Newton's second law of motion. The basic formula force applied on object is F = ma, which implies that net force is equals to product of mass and acceleration of an object. We have an object with the following information, Net applied force on object, F = 125 N
Acceleration of an object, a = 24.0 m/s²
We have to determine mass of object. Using the above force formula, F = M× a
where M --> mass in kilograms
a --> Acceleration in m/s²
F --> net force in Newton
Substitute all known values in above formula, 125 N = M × 24.0 m/s²
=> M = = \(\frac{125}{24}\)
=> M = 5.208 kg
Hence, required value is 5.208 kg.
For more information about Acceleration, visit :
https://brainly.com/question/26246639
#SPJ4
Complete question:
A net force of 125 N is applied to a certain object. As a result, the object accelerates with an acceleration of 24.0 m/s^2. The mass of the object is ?
a) 144 kg
b) 236 kg
c) 5.208 kg
d) 459 kg
Determine if the sequence below is arithmetic or geometric and determine the common difference / ratio in simplest form.16,8,4,...
Answers
Given sequence is geometric sequence and common ratio between consecutive term is
\(16,8,4\)In Arithmetic sequence , common difference between consecutive terms should be equal.
In Geometric sequence, common ratio between consecutive terms should be equal.
Given sequence, 16, 8, 4, ...
Since, common difference = 8 - 16 ≠ 4 - 8 , this is not arithmetic sequence.
Common ratio = T2/T1 = T3/T2 = 8/16 = 4/8 = 1/2 Because common ratio is are equal. Thus, given sequence is geometric sequence.
Hence the sequence is a geometric sequence and the common ratio = 1/2
Can yall help plz??!!!!???

Answers
Answer:
l think that the answer is 91 degrees because they are corresponding angles , that is what I think.
GEOMETRY PROOFS!
Given: JK ≅ ML; ∡JKL ≅ ∡MLK
Prove: △JKL ≅ MLK
refer to attachments
WILL GIVE BRAINLIEST! PLS HELP!

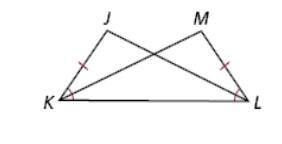

Answers
In ∆JKL and ∆MLK
JK=ML(Given)m<JKL=m<MLK(Given)m<J=m<M(Adjacent angles)Hence
∆JKL≅∆MLK(Side-Angle-Side)
by SAS property of congruency of triangles, ΔJKL and ΔMLK are congruent.
Given that :
JK ≅ ML
∠JKL ≅ ∠MLK
To Prove: △JKL ≅ MLK
Proof:
We know that corresponding angles formed by transversal line are congruent.
Hence ∠JKL = ∠ MLK ...(i)
Now consider triangles ΔJKL and triangles ΔMLK
JK = LM {Given} , This means that Line JK is Congruent to Line LM. Two congruent lines means they are equal. Thus; JK = LM.
∠JKL = ∠ MLK { Using (i) }
KL = KL {common sides}
Hence by SAS property of congruency of triangles, ΔJKL and ΔMLK are congruent.
Hence proved.
Read more about triangle property at :
brainly.com/question/16475105
#SPJ2