You can walk 4/5 of a mile in 1/4 of an hour (15 minutes). How far can you walk in an hour?
Answers
Answer:
0.2
Step-by-step explanation:
Multiply 4/5 and 1/4: Decimal form
.8 • .25
Answer:
3.2 miles in one hour
Step-by-step explanation:
You can walk 4/5 of a mile in 1/4 of an hour (15 minutes). How far can you walk in an hour?
If you can walk 4/5 of a mile in 1/4 of an hour the equation would be:
4/5x = 1/4
multiply both sides by 4:
4(4/5x) = 4(1/4)
3.2 miles per 1 hour
Related Questions
If (6 ki)² = 27-36i, the value of k is
Answers
Answer: k = √27-i
Step-by-step explanation:
In the figure below ∠B=63∘. What is the measure of arc DB in degrees? (4 points) 27 126 54 63

Answers
Answer:
54
Step-by-step explanation:
63 x 2 = 126
180 - 126 = 54
is this a. a function but no one-to-one B. a one-to.one C. not a function

Answers
===================================================
Explanation:
It is a function because it passes the vertical line test. We cannot draw a single vertical line through more than one point on the red curve. Any x input leads to exactly one and only one y output.
A similar test is the horizontal line test. We cannot draw a single horizontal line through more than one point on the red curve, so this red curve passes the horizontal line test. Each y is only paired with one x value only. This helps set up an inverse function.
-----------
In short:
If the curve passes the vertical line test, then we have a function
If the curve passes the horizontal line test, then it is one-to-one.
1.Find the period of the following functions. a) f(t) = (7 cos t)² b) f(t) = cos (2φt²/m)
Answers
Period of the functions: The period of the function f(t) = (7 cos t)² is given by 2π/b where b is the period of cos t.The period of the function f(t) = cos (2φt²/m) is given by T = √(4πm/φ). The period of the function f(t) = (7 cos t)² is given by 2π/b where b is the period of cos t.
We know that cos (t) is periodic and has a period of 2π.∴ b = 2π∴ The period of the function f(t) =
(7 cos t)² = 2π/b = 2π/2π = 1.
The period of the function f(t) = cos (2φt²/m) is given by T = √(4πm/φ) Hence, the period of the function f(t) =
cos (2φt²/m) is √(4πm/φ).
The function f(t) = (7 cos t)² is a trigonometric function and it is periodic. The period of the function is given by 2π/b where b is the period of cos t. As cos (t) is periodic and has a period of 2π, the period of the function f(t) = (7 cos t)² is 2π/2π = 1. Hence, the period of the function f(t) = (7 cos t)² is 1.The function f(t) = cos (2φt²/m) is also a trigonometric function and is periodic. The period of this function is given by T = √(4πm/φ). Therefore, the period of the function f(t) = cos (2φt²/m) is √(4πm/φ).
The period of the function f(t) = (7 cos t)² is 1, and the period of the function f(t) = cos (2φt²/m) is √(4πm/φ).
To learn more about trigonometric function visit:
brainly.com/question/25618616
#SPJ11
PLZ I NEED HELP I HAVE 15 MIN LEFT I WILL GIVE BIG BRAINLYEST TO WHOEVER ANSWERS FIRST AND RIGHT
The least common multiple of the two numbers is 36. Which could be the two numbers?
9 and 12
4 and 6
3 and 8
3 and 12
Answers
Answer:
4 and 6
Step-by-step explanation:
The lest lol
How many and what type of solutions does 5x2−2x+6 have?
1 rational solution
2 rational solutions
2 irrational solutions
2 nonreal solutions
Answers
Answer:
2 nonreal solutions
Step-by-step explanation:
given a quadratic equation in standard form
ax² + bx + c = 0 (a ≠ 0 )
then the nature of the roots are determined by the discriminant
b² - 4ac
• if b² - 4ac > 0 then 2 real and irrational solutions
• if b² - 4ac > 0 and a perfect square then 2 real and rational solutions
• if b² - 4ac = 0 then 2 real and equal solutions
• if b² - 4ac < 0 then no real solutions
5x² - 2x + 6 = 0 ← in standard form
with a = 5 , b = - 2 , c = 6
b² - 4ac
= (- 2)² - (4 × 5 × 6)
= 4 - 120
= - 116
since b² - 4ac < 0
then there are 2 nonreal solutions to the equation
PLEASE HELP!!! The stem-and-leaf plot shows the number of words in the classified ads in a newspaper one day.
How many ads had at least 15, but fewer than 30, words?
123450037230831854759key:10=10
5
14
8
11
Answers
Answer: It's C. 8
Trust me i've done the work for it :)
Use the definition of continuity and the properties of limits to show that the function f(x) = x^2-9/(x^2-x-6)(x^2+6x+9) is continuous at x=2
Answers
Answer:
See below
Step-by-step explanation:
Factor the numerator and denominator
\(\displaystyle f(x)=\frac{x^2-9}{(x^2-x-6)(x^2+6x+9)}\\\\f(x)=\frac{(x+3)(x-3)}{(x-3)(x+2)(x+3)(x+3)}\\\\f(x)=\frac{x-3}{(x-3)(x+2)(x+3)}\)
Because \(x-3\) exists in both the numerator and denominator, there will be a hole at \(x=3\) because the function is not continuous at that point.
If we check if the function is continuous at \(x=2\), we can see that the denominator will not be 0, thus, the function is continuous at \(x=2\).
if its assumptions are met, the analysis of variance technique is appropriate when ____.
Answers
Answer:
comparing the means of three or more groups
Step-by-step explanation:
Which describes the translation of ABCD to A'B'C'D'.
A)
translation 3 units right and 6 units up
translation 6 units right and 3 units up
translation 3 units left and 6 units down
D)
translation 6 units left and 3 units down

Answers
Answer:
Translation 6 units left and 3 units down
Step-by-step explanation:
part 3 to the please help question sorry im asking so many questions

Answers
Answer:
the answer would be 6,600ft
Step-by-step explanation:
I hope this helps!!
A car travels along the highway to Denver at a steady speed. When it begins, it is 300 miles from Denver. After 3 hours, it is 180 miles from Denver. Which function describes the car's distance from Denver?

Answers
Answer:
A, y = -40x+300
Step-by-step explanation:
y=180
x=3
180=-40(3)+300
180=300-120
Select the correct answer.
The variable b varies directly as the square root of c. If b= 100 when c=4, which equation can be used to find other combinations of b and c?
A b= 25c
B.
b = 50√e
OC. b = 200c
OD. b√e 50
-
Reset
Next
Answers
The equation in which b varies directly as the square root of c is b = 50 · √c. (Correct choice: B)
What is the equation of the direct variation between two variables?
In this problem we have a case of direct variation between two variables, which is mathematically described by a direct proportionality model, whose form and characteristics are shown below:
b ∝ √c
b = k · √c (1)
Where k is the proportionality constant.
First, we determine the value of the constant of proportionality by substituting on b and c and clearing the variable: (b = 100, c = 4)
k = b / √c
k = 100 / √4
k = 100 / 2
k = 50
Then, the equation in which b varies directly as the square root of c is b = 50 · √c. (Correct choice: B)
To learn more on direct variation: https://brainly.com/question/14254277
#SPJ1
FILL IN THE BLANK. Study with Quizlet and memorize flashcards containing terms like ____ are the categories by which data are grouped
Answers
Data categorization is a process of organizing and grouping data into meaningful classes or categories.
This process is often used to simplify data and make it easier to understand and analyze. Data categorization involves breaking down a large set of data into smaller, more manageable groups. For example, a company may group customers into categories based on their age, income, or location. Each group can then be analyzed separately to better understand customer behavior. Categorizing data can also help identify trends or patterns that may not be visible when looking at the data as a whole. Categorization can also be used to identify outliers or anomalies in the data. By breaking down the data into smaller groups, it becomes easier to see which elements don’t fit the pattern or are not part of the normal range. Categorizing data can be done using a variety of methods. For example, data can be divided into numerical ranges or grouped into categories such as low, medium, and high. Data can also be grouped using descriptive terms, such as customer type or product type. Once the data is categorized, calculations such as averages, medians, and modes can be used to analyze the data. This can help to identify patterns or trends that can be used to make decisions or draw conclusions.
Learn more about medians here:
https://brainly.com/question/28060453
#SPJ4
Cost of 2 lbs of apples is $ 4.50. What is the cost of 5 lbs of apples in $?
Group of answer choices
Answers
Two cards are selected at random Of a deck of 20 cards ranging from 1 to 5 with monkeys, frogs, lions, and birds on them all numbered 1 through 5 . Determine the probability of the following� a) with replacement.� b) without replacement.The first shows a 2, and the second shows a 4
Answers
(a) The probability of the with replacement is 3/80.
(b) The probability of the without replacement is 15/380.
Two cards are selected at random Of a deck of 20 cards ranging from 1 to 5 with monkeys, frogs, lions, and birds on them all numbered 1 through 5 .
a) with replacement.
5/20 * 3/20 = 3/80.
b) without replacement.
5/20 3/19 = 15/380.
Learn more about probability here;
https://brainly.com/question/29404472
#SPJ4
Last year, Chang opened an investment account with S8500. At the end of the year, the amount in the account had decreased by 6.8% How much is this
decrease in dollars? How much money was in his account at the end of last year?
Decrease in amount:
Year-end amount:
Answers
Answer:
Decrease in amount= $578
Year-end amount= $7,922
Step-by-step explanation:
0.068=x/8500
Isolate x to multiply 0.068 by 8500= 578 which is the decrease in dollars.
so, 8500-578= $7,922 is how much money was in his account at the end of last year.
Decrease in amount: $578
Year-end amount: $7922
What is a percentage?A ratio or value that may be stated as a fraction of 100 is called a percentage. And it is represented by the symbol '%'.
Given:
Last year, Chang opened an investment account with, $8500.
At the end of the year, the amount in the account had decreased by 6.8%
To find the decrease in amount;
6.8% of $8500
= 8500 x 6.8 / 100
= 57800/100
= $578
At the end of the last year, amount,
$8500 - $578
= $7922
Therefore, the required amounts are $578 and $7922.
To learn more about the percentage;
https://brainly.com/question/24159063
#SPJ2
A cuboidal box with dimension 3×3×2 cu. Units is melted into another cuboid whose width is 15 units . Find the length and height of the cuboidformed if l=h
Answers
Answer:
Let's first find the volume of the original cuboidal box:
Volume = Length x Width x Height = 3 x 3 x 2 = 18 cubic units
We can then set up an equation to relate the volume of the original box to the volume of the new cuboid:
Volume of new cuboid = Volume of original box
Let's call the length and height of the new cuboid "x" (since we know that the length and height are the same). We know that the width of the new cuboid is 15 units. Therefore, we can write:
Volume of new cuboid = Length x Width x Height = x x 15 x x = 15x^2
Now we can set up the equation:
15x^2 = 18
Dividing both sides of the equation by 15 gives:
x^2 = 18/15
Simplifying the right side of the equation gives:
x^2 = 1.2
Taking the square root of both sides of the equation gives:
x ≈ 1.095
Therefore, the length and height of the new cuboid are approximately 1.095 units.
A die is thrown once, find the probability of getting an even number and a multiple of 3,
Answers
Answer:
OPA OPA OPA OPA OPA OPA OPA OPA
Step-by-step explanation:
_. ._
\_(``-)_/
Answer:
its by chance yk
Step-by-step explanation:
solve for x 144/25=x/5
Answers
Answer:
Step-by-step explanation:
144/25=x/5
times both sides by 5
144/5=x
simplify
x=144/5 or 28.8
Answer: x= 144/5
Step-by-step explanation:
Cross-Multiply
144/25 = 25x
Swap the sides so you can solve
720 =25x
Divide both sides
25x=720
x=144/5
consider the interval 0≤x≤l . what is the second derivative, with respect to x , of the wave function ψn(x) in this interval? express your answer in terms of n , x , l , and c .
Answers
The second derivative of the wave function ψn(x) in the interval 0≤x≤l is expressed as d²ψn(x)/dx² = -(n²π²c/l²) sin(nπx/l). This result tells us about the curvature of the wave and can help us understand the energy levels of the particle.
To determine the second derivative of the wave function ψn(x) in the interval 0≤x≤l, we first need to understand the function and its derivative. The wave function represents the probability density of finding a particle in a particular state, while the derivative of the wave function gives the momentum of the particle.
Therefore, the second derivative of the wave function gives the curvature of the wave and can tell us about the energy levels of the particle.
Expressing the answer in terms of n, x, l, and c, we can use the Schrödinger equation and the general solution of the wave function to find the second derivative. We know that the wave function ψn(x) is given by ψn(x) = c sin(nπx/l), where c is a constant and n is the energy level.
Taking the derivative of this wave function, we get dψn(x)/dx = (nπc/l) cos(nπx/l). And taking the derivative of this function again, we get the second derivative as d²ψn(x)/dx² = -(n²π²c/l²) sin(nπx/l).
Therefore, the second derivative of the wave function ψn(x) in the interval 0≤x≤l is expressed as d²ψn(x)/dx² = -(n²π²c/l²) sin(nπx/l). This result tells us about the curvature of the wave and can help us understand the energy levels of the particle.
To know more about function visit :
https://brainly.com/question/29769447
#SPJ11
Factor 25x2 10x 1. (5x 1)² (25x 1)(x 1) (5x 1)(5x - 1).
Answers
The factors of the expression 25x² + 10x + 1 will be (5x + 1)². Thus, the correct option is A.
Given that:
Expression, 25x² + 10x + 1
It is a method for dividing a polynomial into pieces that will be multiplied together. At this moment, the polynomial's value will be zero.
Factorize the expression, then we have
25x² + 10x + 1 = 25x² + 5x + 5x + 1
25x² + 10x + 1 = 5x(5x + 1) + 1(5x + 1)
25x² + 10x + 1 = (5x + 1)(5x + 1)
25x² + 10x + 1 = (5x + 1)²
Thus, the correct option is A.
More about the factorization link is given below.
https://brainly.com/question/6810544
#SPJ4
The complete question is given below.
Write the factors of the expression 25x² + 10x + 1.
A. (5x + 1)²
B. (25x + 1)(x + 1)
C. (5x + 1)(5x - 1)
Please help me!
A
B
C
D

Answers
The left and right ends of the normal probability distribution extend indefinitely, never quite touching the horizontal axis. True False
Answers
It is false as the left and right ends of the normal probability distribution extend indefinitely, approaching but never touching the horizontal axis.
The statement is false because the left and right ends of the normal probability distribution do not extend indefinitely. In reality, the normal distribution is defined over the entire real number line, meaning it extends infinitely in both the positive and negative directions. However, as the values move further away from the mean (the center of the distribution), the probability density decreases. This means that although the distribution approaches but never touches the horizontal axis at its tails, the probability of observing values extremely far away from the mean becomes extremely low. Thus, while the distribution theoretically extends infinitely, the practical probability of observing values far from the mean decreases rapidly.
To know more about normal probability distribution,
https://brainly.com/question/33601330
#SPJ11
answer and I’ll leave a good review

Answers
Answer:
d
Step-by-step explanation:
g
Answer:
C
Step-by-step explanation:
They are all more in the modern era
Find the value of k and yz if y is between x and z. x y = 3 k − 2 , y z = 7 k 4 , x z = 4 k 38
Answers
Considering that y is between x and z, we have that:
The value of k is of k = 6.The length of yz is 46 units.How to find the value of k and of yz?We consider that y is between x and z, hence the length of the segment is given by:
xz = xy + yz
The separate lengths are given as follows:
xz = 4k + 38.xy = 3k - 2.yz = 7k + 4.Hence:
4k + 38 = 3k - 2 + 7k + 4.
4k + 38 = 10k + 2
6k = 36
k = 6.
Hence the length of yz is given by:
yz = 7k + 4 = 7(6) + 4 = 42 + 4 = 46 units.
A similar problem, in which the length of a line segment is found, is given by https://brainly.com/question/24778489
#SPJ1
The purchase value of an office computer is $12,350. Its annual depreciation is $1,930.The value of the computer after 9 years is $

Answers
The purchase value of an office compute
Value= 12350
Anuall depreciation = 1930
Value of computer in 9 years t=9
then we can create the formula
\(V(t)=12350-1930t\)then
after 9 years the value of the computer is
\(V(9)=12350-1930(9)\)\(V(9)=12350-17370\)\(V(9)=-5020\)since we have a negative value, the minimum value of the computer is 0
then 3
the value after 9 years of the computer is
$0
New question
V=12780
Depreciation=1947
time = 6 years
\(V(t)=12780-1947t\)\(V(6)=12780-1947(6)\)\(V(6)=12780-11682\)\(V(6)=1098\)in 6 years The value of the computer is 1098
suppose that f(0)=−3 and f′(x)≤8 for all values of x. use the mean value theorem to determine how large f(4) can possibly be. answer: f(4)≤
Answers
The largest value that f(4) can possibly be is 29.
The mean value theorem states that for a function f(x) that is continuous on the closed interval [a, b] and differentiable on the open interval (a, b), there exists a number c in the open interval (a, b) such that:
f(b) - f(a) = f'(c)(b - a)
In this case, we are given that f(0) = -3 and that f'(x) ≤ 8 for all values of x. To determine how large f(4) can possibly be, we can use the mean value theorem with a = 0 and b = 4:
f(4) - f(0) = f'(c)(4 - 0)
Substituting the given values:
f(4) - (-3) = f'(c)(4)
f(4) + 3 = 4f'(c)
Since f'(x) ≤ 8 for all values of x, we can say that f'(c) ≤ 8. Therefore:
f(4) + 3 ≤ 4f'(c) ≤ 4(8) = 32
Therefore, we have:
f(4) ≤ 32 - 3 = 29
Learn more about the differentiation here:
brainly.com/question/954654
#SPJ11
Hello could someone help me I don’t get this? Will name brainliest :D if correct answer please no links
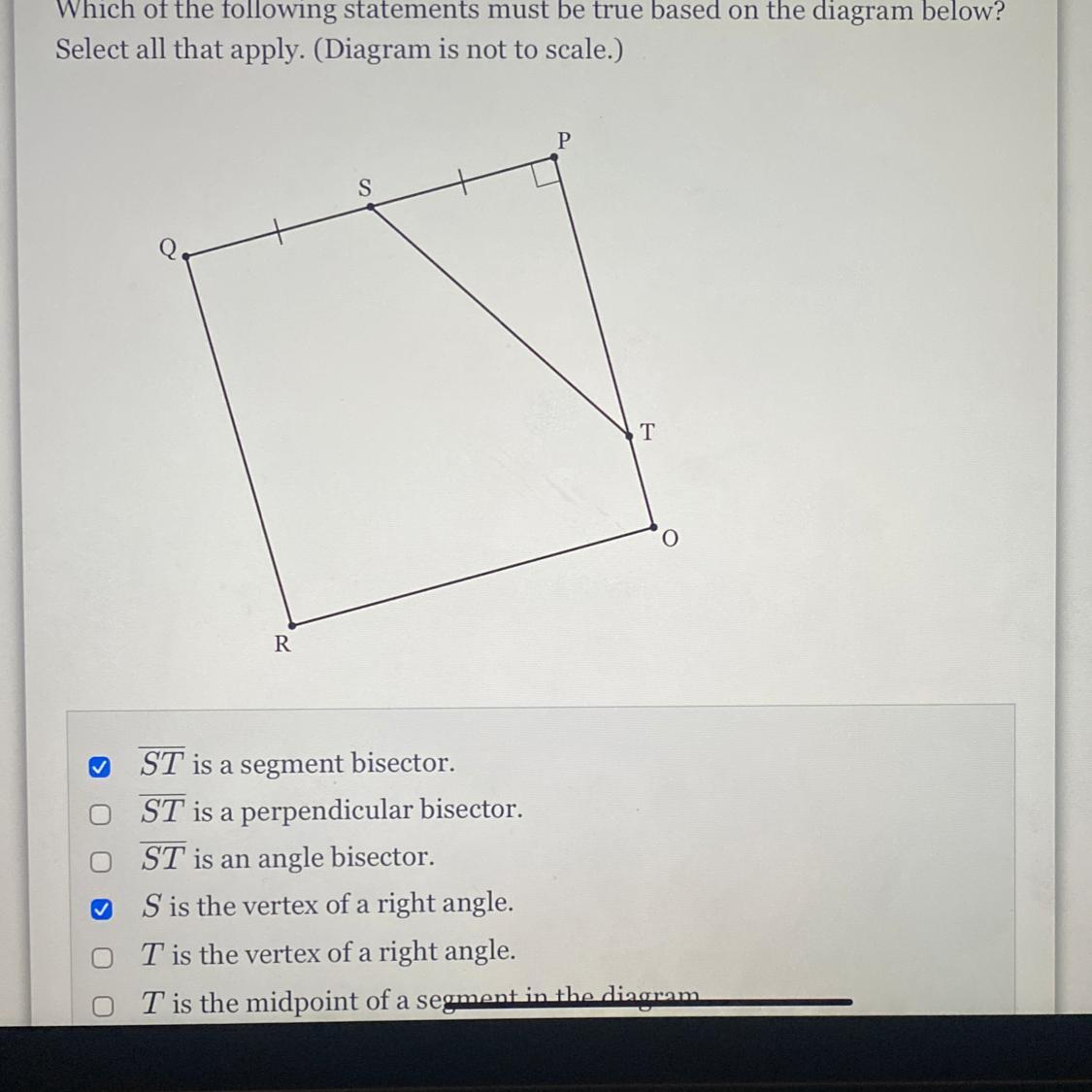
Answers
Answer:
A -- only
Step-by-step explanation:
A segment bisector intersects a segment at its midpoint.
S is the midpoint of segment PQ, so ST is a segment bisector. (It intersects PQ at its midpoint, S.)
No other midpoints are shown in this drawing.
__
A perpendicular bisector is perpendicular to the segment it bisects. None are shown in this drawing.
__
An angle bisector divides an angle into two congruent parts. None are shown in this drawing.
__
The vertex of a right angle is often marked with a small square. Only point P is the vertex of a right angle in this drawing. (We cannot assume OPQR is a square.)
Solve each equation below algebraically or using a flowchart.
8 − a = 17
Answers
Answer:
A = -9Step-by-step explanation: