You are a contractor and charge $65 for a site visit plus an additional $15 per hour for each hour you spend working at the site. Write and solve an equation to determine how many total hours you have to work to earn $950 working at two separate work sites
Answers
Answer:
h = 59 hours
Step-by-step explanation:
Total earnings = fixed charge + variable charge
Fixed charge = $65
Variable charge = $15h
Where, h = number of hours
Total earnings = $950
Total earnings = fixed charge + variable charge
950 = 65 + 15h
Subtract 65 from both sides
950 - 65 = 65 + 15h - 65
885 = 15h
Divide both sides by 15
h = 885 / 15
= 59
h = 59 hours
Related Questions
HELP ASAP geometry 30 points,

Answers
Answer:
Step-by-step explanation:
One
EH = FG
<F = <H
Two
1. DB divides AC into two right angles: BDA and BDC
2. <ABD = CBD
a. write down the regression formula that gets estimated when we perform a test for the stationarity of a time series variable y. what is the null hypothesis of this test? b. briefly describe the steps entailed in determining whether two variables are cointegrated.
Answers
The regression formula estimated when performing a test for the stationarity of a time series variable y is y(t) = α + β*t + ε(t).
a. The null hypothesis of this test is that the time series variable y is non-stationary, meaning it has a unit root.
b. To determine whether two variables are cointegrated, the following steps are typically involved:
1) Identify the two variables: Select two time series variables, denoted as X(t) and Y(t), that are suspected to be related in a long-run equilibrium.
2) Test for unit roots: Conduct unit root tests on both X(t) and Y(t) to determine if they are stationary.
3) Estimate the cointegration regression: If both variables are non-stationary, estimate the cointegration regression model, typically using methods like the Engle-Granger two-step procedure or the Johansen test. This regression model takes the form Y(t) = α + β*X(t) + ε(t).
4) Test for the presence of a cointegrating relationship: Perform hypothesis tests on the estimated coefficients to check if the β coefficient is significantly different from zero, indicating the presence of a cointegrating relationship.
5) Interpret the results: If the null hypothesis of no cointegration is rejected, it suggests that X(t) and Y(t) are cointegrated, meaning they have a long-run relationship.
Cointegration analysis is used to determine whether two variables move together over time, despite being non-stationary individually. It helps in understanding the long-run equilibrium relationship between variables and can be valuable in modeling and forecasting.
Learn more about null hypothesis here:
https://brainly.com/question/30821298
#SPJ11
Consider the line =y+−54x4.
What is the slope of a line parallel to this line?
What is the slope of a line perpendicular to this line?
Answers
Considering the definition of parallel and perpendicular line, the parallel line has a slope of -54 and the perpendicular line has a slope of 1/54.
What is a linear equationA linear equation o line can be expressed in the form y = mx + b
where
x and y are coordinates of a point.m is the slope.b is the ordinate to the origin.Parallel lineParallel lines are two lines that prolonged towards infinity never touch.
Two lines are parallel if they have the same slope.
Perpendicular linePerpendicular lines are lines that intersect at 90° angles. If you multiply the slopes of two perpendicular lines, you get –1.
Slope of parallel line in this caseIn this case, the line is y= -54x -4.
where:
the slope is -54.the ordinate to the origin is -4.Since two lines are parallel if they have the same slope, the parallel line has a slope of -54.
Slope of perpendicular line in this caseIf you multiply the slopes of two perpendicular lines, you get –1. So:
-54 × slope perpendicular line= -1
slope perpendicular line= (-1)÷ (-54)
slope perpendicular line= 1/54
The perpendicular line has a slope of 1/54.
Learn more about parallel and perpendicular line:
brainly.com/question/7197064
brainly.com/question/11470863
brainly.com/question/7280013
#SPJ1
Classify the quadric surface. 4x2 - y2 - z2 = 1 a. hyperbolic paraboloid b. elliptic cone c. Hyperboloid of two sheets d. hyperboloid of one sheet e. ellipsoid
Answers
The given equation (4x² - y² - z² = 1) is classified under Hyperboloid of two sheets.
What is Hyperboloid equation?
When a hyperbola is rotated around one of its axes, an open surface is created that is known as a hyperboloid. The surface's general equation is written as (x²/ a²) + (y² / b²) - (z² / c²) = 1
if the surface's transverse axis is along the x axis, its centre is at the origin, and a, b, and c are its primary semi-axes.
As per question given that,
here is the equation of the quadratic surface is,
4x² - y² - z² = 1
Thus surface is a hyperboloid of two sheets.
The sketch of this quadratic surface is the sketch in the 2nd option which is shown below.
i.e. in the upper right corner.
To learn more about hyperboloid from the given link.
https://brainly.com/question/3351710
#SPJ4

Question 7
It is given that a = (-3, m) and b = (4,3). If the angle between vector a and b is an
obtuse angle, what is true for the value of m?
A) m<4
B) m<4 and doesn’t equal -9/4
C) m>4
D) m doesn’t equal 4 and m > -9/4
Answers
After answering the given query, we can state that We know that equation (-12 + 3m) must be negative because cos 0, which means that 3m 12 or m 4. As a result, choice A) m 4 is correct.
What is equation?The equals sign (=) is used in mathematical equations to denote equality between two assertions. A mathematical statement that establishes the equality of two mathematical expressions is known as an equation in mathematics. For instance, the equal sign places a space between the integers in the equation 3x + 5 = 14. The relationship between the two lines on either side of a character can be expressed mathematically. Frequently, the logo and the specific component of software are the same. such as, for example, 2x - 4 = 2.
Between two vectors a and b, the dot product is
A = B given by |a| |b| cos
where is the angle between the vectors a and b, and |a| and |b| are their relative magnitudes. We are aware that cos 0 because we are aware that the angle between vectors a and b is acute
a · b = (-3)(4) + m(3) = -12 + 3m
The size of the vector an is:
|a| = √((-3)^2 + m^2) = √(9 + m^2)
The strength of the vector b is:
|b| = √(4^2 + 3^2) = 5
We can now determine the cos using the dot product formula:
cos = (a b) / (|a | |b|) = (-12 + 3m) / (5 (9 + m2)
We know that (-12 + 3m) must be negative because cos 0, which means that 3m 12 or m 4.
As a result, choice A) m 4 is correct.
To know more about equation visit:
https://brainly.com/question/649785
#SPJ1
Please work me through the steps.

Answers
Answer:-6\(x^{12}\)
Step-by-step explanation:
Open the brackets
-x is the same as -1x
(2\(x^{3}\) x -\(x\))(3\(x^{8}\))
The bases will be multiplied while the powers will be multipled-2\(x^{4}\) x 3\(x^{8}\)
In the law of indices(multiplication), provided the bases are equal,they are to be added.-6 \(x^{4} +x^{8}\)
= -6\(x^{12}\)
which equation represents the relationship between the X values and the Y values in the table
Answers
Answer:
y=3x-4
Step-by-step explanation:
Click on the number line below to show the approximate location of 19 on the number line.

Answers
Answer:
Between 4 and 5
Step-by-step explanation:
The closest square numbers are 16 and 25, so it’s in between 4 and 5
Inx 17. Evaluate the integral (show clear work!): S * dx
14. Write an expression that gives the area under the curve as a limit. Use right endpoints. Curve: f(x) = x? from x = 0 to x = 1. Do not att
Answers
For question 17, there is no function or limits of integration provided, so I cannot evaluate the integral. Please provide the necessary information.
For question 14, the prompt seems to be cut off. It says "Write an expression that gives the area under the curve as a limit," but then it cuts off with "Do not att." Please provide the complete prompt so I can assist you better.
The integral ∫[0 to 1] x² dx evaluates to 1/3.
To evaluate this integral, we can use the power rule for integration. Applying the power rule, we increase the power of x by 1 and divide by the new power. Thus, integrating x² gives us (1/3)x³.
To evaluate the definite integral from x = 0 to x = 1, we substitute the upper limit (1) into the antiderivative and subtract the result when the lower limit (0) is substituted.
Using the Fundamental Theorem of Calculus, the area under the curve is given by the expression A = ∫[0 to 1] f(x) dx. For this case, f(x) = x².
To approximate the area using right endpoints, we can use a Riemann sum. Dividing the interval [0, 1] into subintervals and taking the right endpoint of each subinterval, the Riemann sum can be expressed as lim[n→∞] Σ[i=1 to n] f(xᵢ*)Δx, where f(xᵢ*) is the value of the function at the right endpoint of the i-th subinterval and Δx is the width of each subinterval.
In this specific case, since the function f(x) = x² is an increasing function on the interval [0, 1], the right endpoints of the subintervals will be f(x) values.
Therefore, the area under the curve from x = 0 to x = 1 can be expressed as lim[n→∞] Σ[i=1 to n] (xi*)²Δx, where Δx is the width of each subinterval and xi* represents the right endpoint of each subinterval.
To learn more about integral click here
brainly.com/question/31059545
#SPJ11
PLEASE HELP!!!!!!!
The pentagon on the left is a reflection of the pentagon on the right.
The pentagon is reflected over line ______?

Answers
Answer:
A
Step-by-step explanation:
If you reflect over line A both pentagons are equally spaced in proportion to the line
A ship sails 5 km on a bearing of 060° and then for 4 km on a bearing of 300°. Calculate: (a) her distance from her starting point, correct to three significant figures. (b) her bearing from her starting point, correct to the nearest degree.
Answers
The ship's distance from its starting point is 7.810 km and the ship's bearing is 49°.
(a) Distance from the starting point:
To find the distance, we have to consider the two legs of the ship's journey as vectors and use the Pythagorean theorem.
Using the cosine rule, we can find the magnitude of the resultant vector:
=√(25 + 16 - 40cos(240°))
=√(41 - 40cos(240°))
=√(41 + 40 * 0.5)
=√(41 + 20)
=√(61)
≈ 7.810 km (rounded to three significant figures)
(b) Bearing from the starting point:
To find the bearing, we have to use the tangent of the angle between the resultant vector and the east direction.
=tan((4 sin(240°)) / (5 - 4 cos(240°)))
=tan((-4 * 0.866) / (5 - 4 * 0.5))
=tan((-3.464) / (5 - 2))
=tan((-3.464) / 3)
=tan(-1.154)
≈ -49° (rounded to the nearest degree)
Therefore, the ship's bearing is 49° and is at 7.810 km from its starting point.
Learn more about the ship's bearing from the given link.
https://brainly.com/question/33785503
6. A sphere-shaped globe is packaged in the regular hexagonal prism-shaped box shown. The area of the base is 260 square inches. Find the volume of the box.
7. The globe has a diameter of 16 inches. What volume of packing material is needed to fill the space in the box not taken up by the globe? Round your answer to the nearest cubic inch

Answers
The Volume of packing material needed to fill the space in the box not taken up by the globe is 21,256.33 cubic inches.
6. A sphere-shaped globe is packaged in the regular hexagonal prism-shaped box shown. The area of the base is 260 square inches.
Find the volume of the box.The base of the regular hexagonal prism is a hexagon that is divided into 6 equal equilateral triangles with each triangle having a height of x and the base as 18.
The area of each equilateral triangle is equal to area of regular hexagon divided by 6.Area of the base=260 sq inArea of each equilateral triangle=(1/6) * 260= 43.33 sq in
Let's use Pythagorean Theorem to find the height of the equilateral triangle.x² = 18² - (18/2)²x² = 18² - 9²x² = 225x = 15 inTherefore,
the volume of the box is given byV = BhB = area of base = 260 cu inh = height of box = 6x = 6(15) = 90 inVolume of the box = V = Bh = 260(90) = 23,400 cubic inches
7. The globe has a diameter of 16 inches. What volume of packing material is needed to fill the space in the box not taken up by the globe? Round your answer to the nearest cubic inch r be the radius of the sphere-shaped globe with diameter 16, then r = 8 inches. We have to find the volume of the space in the box not taken up by the globe which is given by the difference in volume of the box and the volume of the sphere-shaped globe.
The volume of the sphere-shaped globe is given by 4/3πr³ and the volume of the packing material is given by the difference of the volume of the box and the volume of the sphere-shaped globe.
Volume of the sphere-shaped globe=4/3 * π * 8³=2143.67 cubic inchesVolume of the packing material= Volume of the box-Volume of the sphere-shaped globe= 23,400 - 2143.67 = 21,256.33 cubic inches
Hence, the volume of packing material needed to fill the space in the box not taken up by the globe is 21,256.33 cubic inches.
To know more about Volume.
https://brainly.com/question/30610113
#SPJ8
The ratio of two numbers in 7:5 if the difference between these numbers is 12, find the numbers
Answers
Answer:
5
Step-by-step explanation:
If you multiply each side by 5 to get 42:30 then subtract 42 by 30, 12 is leftover.
Answer:
The numbers should be 42 and 30
Step-by-step explanation:
Okay, so the equation should be:
7x - 5x = 12
2x = 12
x = 6
and find the numbers:
7 x 6 = 42
5 x 6 = 30
pleaseeee helpppppp!!!!
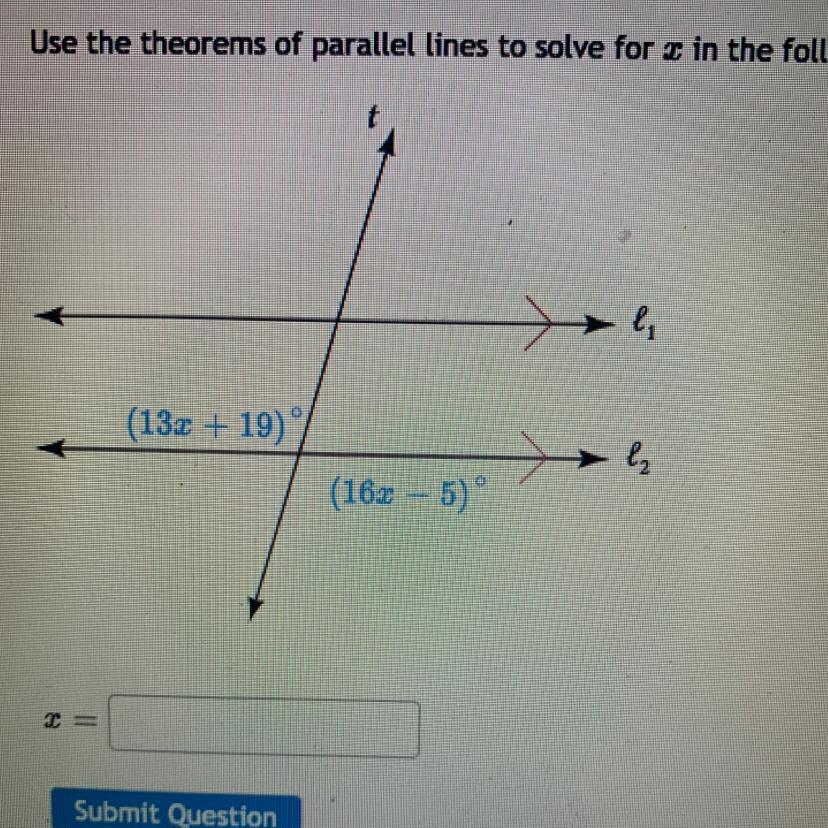
Answers
Answer:
x=8
Step-by-step explanation:
The angles shown are vertical angles and vertical angles are equal
13x+19 = 16x -5
Subtract 13x from each side
13x-13x+19 = 16x-13x -5
19 = 3x-5
Add 5 to each side
19+5 = 3x-5+5
24 = 3x
Divide by 3
24/3 = 3x/3
8 = x
Answer:
x = 8
Step-by-step explanation:
The angles shown are vertical angles
Vertical angles are congruent
Hence, 13x + 19 = 16x - 5
We now solve for x using the equation we just created
13x + 19 = 16x - 5
Subtract 13 x from both sides
19 = 3x - 5
Add 5 to both sides
24 = 3x
Divide both sides by 3
x = 8
The digits of a 2 digit number differ by 3. Is the digits are interchanged, and the resulting number is added to the original number, we get 143. What can be the number?
Answers
Answer:
58
Step-by-step explanation:
Hello, let's note the two digits a and b. the first number 'ab' can be written as 10a +b. For instance if this is 24 it can be written 20 + 4.
If the digits are interchanged the number become 'ba' so 10b + a
We can say that 10a + b + 10b + a = 143
11(a+b)=143
We divide by 13 both sides and we take
a+b = 143/11 = 13
and we know that the digits differ by 3 so b = a + 3
then a + b = a + 3 + a = 2a + 3 = 13
so 2a = 10 and then a = 5
Finally, b = 5+3=8 so the number is 58.
And we can verify that 58 + 85 = 143.
Thanks
Answer:
Let the unit digit be x and tens digit be x + 3Therefore, the original number = 10(x + 3) + xOn interchanging, the number formed = 10x + x + 3❍ According to Question now,
➥ 10(x + 3) + x + 10x + x + 3 = 143
➥ 10x + 30 + 12x + 3 = 143
➥ 22x + 33 = 143
➥ 22x = 143 - 33
➥ 22x = 110
➥ x = 110/22
➥ x = 5
__________________...Therefore,
The unit digit number = x = 5
The tens digit number = x + 3 = 5 + 3 = 8
__________________...The original number = 10(x + 3) + x
The original number = 10(5 + 3) + 5
The original number = 50 + 30 + 5
The original number = 85
Hence,the original number is 85.
Which explains whether FGH îs congruent to FJH?
Answers
Based on the definition of congruent triangles, we can state that: C. They are not congruent because only one pair of corresponding sides is congruent.
What is a pair of Congruent Triangles?Congruent triangles refer to a pair of triangles that possess identical shape and size. If two triangles are congruent, it implies that their corresponding sides and angles are precisely equal.
The image that is attached below shows the diagram of triangles FGH and FJH. We see that only one pair of sides are congruent (FH = FH).
This is not enough to conclude that both triangles are congruent. Therefore, we can conclude that:
C. They are not congruent because only one pair of corresponding sides is congruent.
Learn more about congruent triangles on:
https://brainly.com/question/2938476
#SPJ1
In finance, we need to do partial observations of data and estimate the data generating process (DGP) -- for example, log-normal returns. Sometimes, we can observe only the data points of a certain process, but we don't know what is the function generating the process. Consider the following graph is a plot of the f ′
(x), of a function f(x) given. What is the underlaying function ( f(x −
i)) that is the generator of the observed points in the plot f ′
(x −
i), for points x −
1=−1,x −
2=−0.9,…,x −
n=1?
Answers
The underlying function f(x - i) that generates the observed points f'(x - i) in the plot can be determined by integrating the observed points. By integrating f'(x - i), we can obtain f(x - i) up to a constant of integration.
The constant of integration can be determined by incorporating additional information or constraints related to the problem or by considering the behavior of the function at a specific point.
To find the underlying function f(x - i) that generates the observed points f'(x - i), we need to integrate the observed points.
Integration is the reverse process of differentiation, so by integrating f'(x - i), we can recover f(x - i) up to a constant of integration.
The constant of integration arises because integration does not provide a unique solution.
The constant represents an arbitrary additive term that can vary depending on the specific problem or additional constraints.
To determine the constant of integration, we may need additional information or consider specific conditions related to the problem.
It is also important to note that the accuracy of estimating the underlying function f(x - i) depends on the quality and quantity of the observed data points f'(x - i). More data points and precise measurements can lead to a better estimation of the underlying function.
Additionally, the behavior of the function at a specific point can provide valuable insights for determining the constant of integration and refining the estimation of the underlying function.
To learn more about integration visit:
brainly.com/question/31954835
#SPJ11
Integrate by hand the following functions: adr b) (42³-2r+7) dz Upload Choose a File
Answers
The integral of (42³ - 2r + 7) dz is equal to (42³ - 2r + 7)z + C.
To integrate the function (42³ - 2r + 7) dz, we treat r as a constant and integrate with respect to z. The integral of a constant with respect to z is simply the constant multiplied by z:
∫ (42³ - 2r + 7) dz = (42³ - 2r + 7)z + C
where C is the constant of integration.
Note: The integral of a constant term (such as 7) with respect to any variable is simply the constant multiplied by the variable. In this case, the variable is z.
Know more about integration here:
https://brainly.com/question/31744185
#SPJ11
Enter your answer and show all the steps that you use to solve this problem in the space provided.
Combine like terms. What is a simpler form of the expression?
−3(−4y+3)+7y
help pls
Answers
Answer:
19y - 9
Step-by-step explanation:
- 3(- 4y + 3) + 7y ← multiply each term in the parenthesis by - 3
= 12y - 9 + 7y ← collect like terms
= 19y - 9
Evaluate the accuracy of the following statement: When the mean of a data set is large, the standard deviation will be large.
Answers
By the given explanations, When the mean of a data set is large, the standard deviation will be large.
Mean of a Data:The Mean of the data represents the average of the data. In other words, the mean of the data is the ratio of the sum of the observations to the number of observations.
Standard deviation:The standard deviation is a measure of how dispersed values are in a dataset in relation to the mean. The more distributed evenly the values within a sample, the greater the standard deviation value.
What if the standard deviation is larger?As we know standard deviation measures how much the entire data set will differ from the mean. This means the larger the standard deviation means, the more spread or variation in the data. Similarly, the smaller standard deviations mean that most of the data is clustered around the mean.
Therefore,
Here we can conclude that When the mean of a data set is large, the standard deviation will be large.
Learn more about Standard deviation at
https://brainly.com/question/23907081
#SPJ4
I need the blank angles answers with the reason of justification please

Answers
Answer:
We had this question last week let me check my book real quick.
Find the term of the following arithmetic sequence. 15,22 , 29 , 36 ,
Answers
Answer:
The sequence can be continued by adding 7 to each number.
Step-by-step explanation:
15 + 7 = 22
22 + 7 = 29
29 + 7 = 36
36 + 7 =...... 43 would be your next number
A park at the end of a city block is a right triangle with legs 150 ft and 200 ft long. Make a scale drawing of the park using the scale, 1. 5 in : 100 ft
Answers
To create a scale drawing of the park, we can use the given scale of 1.5 in : 100 ft.
First, we need to determine the dimensions of the scale drawing using the given lengths of the legs of the right triangle.
Let's calculate the dimensions of the park in inches:
Length of one leg in inches = (Length of one leg in feet) * (Scale factor)
Length of one leg in inches = 150 ft * (1.5 in / 100 ft) = 2.25 in
Similarly, for the other leg:
Length of the other leg in inches = 200 ft * (1.5 in / 100 ft) = 3 in
Now, using these dimensions, we can create a scale drawing of the park:
1. Draw a right triangle shape on a piece of paper or a drawing software.
2. Label one leg with a length of 2.25 inches and the other leg with a length of 3 inches.
3. Ensure that the right angle between the legs is correctly represented.
4. Optionally, add labels or markings to indicate the measurements.
To know more about measurements visit:
brainly.com/question/20727341
#SPJ11
perform the following calculations with the correct significant figures 0.0879/0.98
Answers
The correct significant figure of 0.0879/0.98 is 0.08989796. (rounded to six significant figures)
Significant FiguresThe meaningful digits in a measured or computed number are known as significant figures. They are used to convey the degree of uncertainty in a value and represent the accuracy of the measurement. You must first establish the number of significant figures in each value being utilized before you can execute a computation with significant figures. When doing the computation, use the same number of decimal places as the value with the fewest significant figures. The final step is to round the result to the appropriate number of significant digits.
According to the question
Both numbers in the calculation 0.0879/0.98 have four significant digits. The result, after performing the calculation, is 0.08989796. We look at the final digit (7) in the response to determine the right amount of significant digits to round to. The preceding digit (9) is rounded up if the digit is 5 or above. In this instance, the solution, rounded to six significant numbers, is 0.0899.
To know more about significant figures on brainly : brainly.com/question/29153641
#SPJ4
What are the zeros of the function h (x) = x² + 3x - 8?
A
x = -8 and x = -2
OB
x= -8 and x = 2
cx = -2 and x = 8
OD x = 2 and x = 8

Answers
The following are the zeros for the function h (x) = x2 + 3x - 8: - x= -4 and x=2.
Describe functions.Given a collection of inputs X (domain) and a set of potential outputs Y (codomain), a function is more technically defined as a set of ordered pairings (x,y) where xX and yY with the caveat that there can only be one ordered pair with the same value of x. The function notation f:XY can be used to express that f is a function from X to Y.
The function's zero is a value of x that makes it equal to zero. In other words, the equation f(x) = 0 leads to a zero.
By putting h(x) equal to zero and figuring out x, we may determine the zeroes for the function h(x) = x2 + 3x - 8.
h(x) = x² + 3x - 8 = 0
We may factor the left side of the equation to find x:
x² + 3x - 8 = (x-2)(x+4) = 0
We set each factor to zero and solve for x to discover the zeroes:
x-2 = 0 or x+4 = 0
x = 2 or x = -4
Consequently, the function's zeros are x = 2 and x = -4.
So, A is the right response. x = -4 and x = 2
To know more about functions visit:
https://brainly.com/question/29120892
#SPJ1
The complete question is
What are the zeros of the function h (x) = x² + 3x - 8?
A. x = -4 and x = -2
B. x= -8 and x = 2
C. x = -2 and x = 8
D. x = 2 and x = 8
A student writes the equation for a line that has a slope of -6 and passes through the point (2, –8).
y -(-8) = -6(x - 2)
y -(-8) = -6x + 12
y -(-8) + 8 = -6x + 12 + 8
y = -6x + 20
Explain why the work is not correct.
(it has to be in a sentence or paragraph!)
Answers
Replace each ____ with >,< , or = to make a true statement.
3/4in. ____ 5/8 in.
Answers
The statement "3/4 in. > 5/8 in." is true. To determine the relationship between 3/4 in. and 5/8 in., we can compare their values. In this case, 3/4 in. is greater than 5/8 in.
To compare fractions, we can convert them to a common denominator. The common denominator of 4 and 8 is 8.
Converting 3/4 to an equivalent fraction with a denominator of 8, we multiply the numerator and denominator by 2:
3/4 = (3*2)/(4*2) = 6/8
Now we can compare 6/8 and 5/8. Since the denominators are the same, we only need to compare the numerators. In this case, 6 is greater than 5. Therefore, 3/4 in. is greater than 5/8 in., and the statement "3/4 in. > 5/8 in." is true.
Learn more about fractions here: brainly.com/question/10354322
#SPJ11
if f(x)+5x -2 and g(x)+2x+1 find (f+g)(x)
Answers
9514 1404 393
Answer:
(f+g)(x) = 7x -1
Step-by-step explanation:
(f+g)(x) = f(x) +g(x)
= (5x -2) +(2x +1)
(f+g)(x) = 7x -1
Consider the following vector field.
F(x, y, z) =
9ex sin(y), 2ey sin(z), 8ez
sin(x)
(a)
Find the curl of the vector field.
curl(F) =
(b)
Find the divergence of the vector field.
div(F) =
Answers
The curl of the vector field
curl(F) = -2ey cos(z)i + 8ez cos(x)j - 9ex cos(y)k
The divergence of the vector field
div(F) = 9e^x sin(y) + 2e^y sin(z) + 8e^z
To find the curl of the vector field F(x, y, z) = 9ex sin(y), 2ey sin(z), 8ez sin(x), we need to compute the determinant of the curl matrix.
(a) Curl of F:
The curl of a vector field F = P(x, y, z)i + Q(x, y, z)j + R(x, y, z)k is given by the following formula:
curl(F) = (∂R/∂y - ∂Q/∂z)i + (∂P/∂z - ∂R/∂x)j + (∂Q/∂x - ∂P/∂y)k
In this case, we have:
P(x, y, z) = 9ex sin(y)
Q(x, y, z) = 2ey sin(z)
R(x, y, z) = 8ez sin(x)
Taking the partial derivatives, we get:
∂P/∂y = 9ex cos(y)
∂Q/∂z = 2ey cos(z)
∂R/∂x = 8ez cos(x)
∂R/∂y = 0 (no y-dependence in R)
∂Q/∂x = 0 (no x-dependence in Q)
∂P/∂z = 0 (no z-dependence in P)
Substituting these values into the curl formula, we have:
curl(F) = (0 - 2ey cos(z))i + (8ez cos(x) - 0)j + (0 - 9ex cos(y))k
= -2ey cos(z)i + 8ez cos(x)j - 9ex cos(y)k
Therefore, the curl of the vector field F is given by:
curl(F) = -2ey cos(z)i + 8ez cos(x)j - 9ex cos(y)k
(b) Divergence of F:
The divergence of a vector field F = P(x, y, z)i + Q(x, y, z)j + R(x, y, z)k is given by the following formula:
div(F) = ∂P/∂x + ∂Q/∂y + ∂R/∂z
In this case, we have:
∂P/∂x = 9e^x sin(y)
∂Q/∂y = 2e^y sin(z)
∂R/∂z = 8e^z
Substituting these values into the divergence formula, we have:
div(F) = 9e^x sin(y) + 2e^y sin(z) + 8e^z
Therefore, the divergence of the vector field F is given by:
div(F) = 9e^x sin(y) + 2e^y sin(z) + 8e^z
Learn more about divergence of the vector this link:
https://brainly.com/question/30907324
#SPJ11
The cube with side 2 is cut from the corner of rectangular prism with dimensions 4×3×5. Find the volume and total surface area of the new object.
Answers
Answer:
Volume: 52 Units Squared
Surface Area: 94 units.
Step-by-step explanation:
The volume is relatively simple to find. Just subtract the original volume by the 2x2x2 cube's volume. The original volume is 60. The cube's volume is 2x2x2 which is 8. 60-8=52.
The surface area is harder to find. Try to envision the corner of the rectangle being cut out. We see that each side of the cube has a surface area of 2x2 which is 4. In the picture, we see that three sides of the rectangle has been partially removed. But since each side of the cube has an equal surface area, it is safe to minus 3 of the sides that has been partially removed by 3. However, since that it is the corner, the "dent" that the cube made in the rectangle also needed to be counted. As we said, each of the sides of a cube has a surface area of 4, so since that the dent has 3 sides, we see that the surface area of the dent is 4x3 which is 12. Now we need to count the unaffected sides of the rectangle. There are three of them. Just multiply the edges to find the surface area of each side. Add all of the values up: 11+16+12+8+15+12+20=94 units.