Yochanan walked from home to the bu top at an average peed of
mph. He immediately got on hi chool bu and traveled at an average peed of
mph until he go to chool. The total ditance from hi home to chool i
mile, and the entire trip took
hour. The following ytem of equation repreent thi:
Answers
Distance covered by Yochanan by walking = 5 km
Distance covered by Yochanan by bus = 30 km
Given the values in the question,
The average speed of Yochanan when he walked to the bus stop from home = 5 km/h
The average speed of the bus till Yochanan reached his school = was 60 km/h
The total distance between his school from home = is 35 km
Time is taken by the entire trip = 1.5 hours
Relation between Distance, Time, and speed,
⇒ Average Speed = \(\frac{Distance}{Time}\)
Let us consider that Yochanan walked = a km
The bus travelled = 35 - a
We know that the total time is constant so,
⇒ T = T1 + T2
⇒ 1.5 = \(\frac{x}{5} + \frac{35-a}{60}\)
Solving for a,
⇒ 1.5 = \(\frac{12a + 35 - a}{60}\)
⇒ 11 a + 35 = 90
⇒ 11 a + 55
⇒ a = 5
The distance covered by Yochanan by walking = a = 5 km
Distance covered by bus = 35 - a
= 35 - 5
= 30 km
Therefore, the distance covered by Yochanan by walking = is 5 km, distance covered by Yochanan by bus = is 30 km
To learn more about Linear Equations,
https://brainly.com/question/25858757
#SPJ4
Yochanan walked from home to the bus stop at an average speed of 5 km/h he immediately got on his school bus and traveled at an average speed of 60 km/h until he got to school. the total distance from his home to school is 35 kilometers, and the entire trip took 1.5 hours. how many kilometers did Yochanan cover by walking, and how many kilometers did he cover by traveling on the bus? Yochanan walked kilometers and traveled kilometers on the bus.
Related Questions
given that abcd is a rhombus prove ac bisects BCD

Answers
Answer:
Step-by-step explanation:

Which inequality is represented by this graph?

Answers
The linear equality for the given graph is x > 0.
Option (B) is correct.
What is linear equality?
In mathematics, a linear inequality is an inequality that involves a linear function. A linear inequality contains one of the symbols of inequality. It shows the data which is not equal in graph form.
The hollow circle in the linear equality shows that the point should be excluded and the line is going towards the positive x-axis.
So we can prepare the linear equality as
x > 0
Hence, the linear equality for the given graph is x > 0.
To learn more about linear equality, visit:
https://brainly.com/question/21103162
#SPJ1
Refer to Table \( \$ 6.1 \)-Factors for Computing Control Chart Limits \( (\underline{3} \) sigma) for this problem. Thirty-five samples of size 7 each were taken from a fertilizer-bag-filling machine
Answers
The control chart limits (3 sigma) for the fertilizer-bag-filling machine can be computed using Table $6.1.
How can the control chart limits be computed using Table $6.1 for the given problem?To compute the control chart limits (3 sigma) using Table $6.1 for the fertilizer-bag-filling machine, follow these steps:
Determine the sample size: In this problem, each sample consists of 7 observations.
Calculate the average range (R): For each sample, calculate the range by subtracting the smallest observation from the largest observation. Then, calculate the average range across all 35 samples.
Find the appropriate value from Table $6.1: Locate the row in Table $6.1 corresponding to the sample size (7) and find the factor associated with 3 sigma. This factor represents the number of standard deviations for the control limits.
Compute the control limits: Multiply the average range (R) by the factor obtained from Table $6.1 to determine the width of the control limits. Then, subtract this width from the overall average of the process data to obtain the lower control limit, and add the width to the overall average to obtain the upper control limit.
Learn more about control chart limits
brainly.com/question/29756559
#SPJ11
for each geometric sequence given, write the next three terms a4, a5, and a6. (a) 3, 6, 12, a4 = a5 = a6 = (b) 256, 192, 144, a4 = a5 = a6 = (c) −0.5, 3, −18, a4 = a5 = a6 =
Answers
The next three terms for the geometric sequence 3, 6, 12 is 24,48,96 ,for 256, 192, 144 is 108,81,60.75 and for −0.5, 3, −18 is -108,-648,-3488.
(a) 3, 6, 12, ...
To find the common ratio, divide the second term by the first term:
6 / 3 = 2
Now, multiply the last given term (12) by the common ratio (2) to find the next terms:
a4: 12 * 2 = 24
a5: 24 * 2 = 48
a6: 48 * 2 = 96
So, a4 = 24, a5 = 48, and a6 = 96.
(b) 256, 192, 144, ...
To find the common ratio, divide the second term by the first term:
192 / 256 = 0.75
Now, multiply the last given term (144) by the common ratio (0.75) to find the next terms:
a4: 144 * 0.75 = 108
a5: 108 * 0.75 = 81
a6: 81 * 0.75 = 60.75
So, a4 = 108, a5 = 81, and a6 = 60.75.
(c) -0.5, 3, -18, ...
To find the common ratio, divide the second term by the first term:
3 / (-0.5) = -6
Now, multiply the last given term (-18) by the common ratio (-6) to find the next terms:
a4: -18 * -6 = 108
a5: 108 * -6 = -648
a6: -648 * -6 = 3888
So, a4 = 108, a5 = -648, and a6 = 3888.
Learn more about common ratio for the geometric sequence : https://brainly.com/question/1509142
#SPJ11
if my avg is a 96 and my final exam is a 75 which is 25% of my whole grade what will my final grade be
Answers
Step-by-step explanation:
That means the 96 is 75% of your grade
96 (.75) + 75 (.25) = 90.75 final grade
Find the value of x.

Answers
Answer:
73 degrees
Step-by-step explanation:
A triangle always has a total internal angular sum of 180 degrees.
Subtract both 48 and 59 from 180 to get 73.
Hope this helps!
Put the following equation of a line into slope-intercept form, simplifying all
fractions.
8x + 6y = -54
Answers
Answer:
y = - 4/3x - 9
Step-by-step explanation:
Answer:
\(y = -\frac{4}{3}x - 9\)
Step-by-step explanation:
The standard form of linear equation is: Ax + By = C, where A, B, and C are integers; A and B ≠ 0, and A is a non-negative integer.
Given the linear equation in standard form, 8x + 6y = -54, we can transform this equation into its slope-intercept form, y = mx + b.
First, subtract 8x from both sides:
8x + 6y = - 54
8x - 8x + 6y = - 8x - 54
6y = -8x - 54
Divide both sides by 6 to isolate y:
\(\frac{6y}{6} = \frac{-8x - 54}{6}\)
\(y = -\frac{4}{3}x - 9\) ⇒ This is the slope-intercept form where the slope, m = \(- \frac{4}{3}\), and the y-intercept, b = -9.
Colin and Brian were playing darts. Colin scored 16. Brian scored 63 more than Colin. What was their combined score?
Answers
Answer:
79
Step-by-step explanation:
Joven's scores in five of his quizzes in mathematics are 85, 88, 95, 86, and 92. if he needs an average quiz grade of 90 to be able to maintain his required grade for his scholarship, what score must he get for his sixth quiz?
Answers
Answer:
If, he got 94 marks for his sixth quiz, then, he will be able to maintain his required grade for his scholarship.
Step-by-step explanation:
given-
Joven's scores in five of his quizzes in mathematics are 85, 88, 95, 86, and 92.
let, the x score he gets for his sixth quiz.
then, he will be able to maintain his required grade for his scholarship.
he needs an average quiz grade of 90 to maintain his required grade for his scholarship.
according to the question--
using the formula of average=>
(85+88+95+86+92+x)/6=90
=>x=540-446
=>x=94
if, he got 94 marks for his sixth quiz, then, he will be able to maintain his required grade for his scholarship.
link-https://brainly.com/question/1438042
#SPJ4
Two functions are represented below what is the difference in rate of change between functional a function A and function B. Be sure to include the rate of change of each function in your question answer(8.F.2)
Answers
The difference in the rate of change between Function A and function B is -2.
The difference in the rate of change between function A and function B, we first need to identify the rate of change for each function. The rate of change, also known as the slope, represents how much the dependent variable (y) changes for every unit increase in the independent variable (x).
Let's assume function A is represented by the equation y = 2x + 3, and function B is represented by the equation y = 4x - 1.
For function A: y = 2x + 3, the coefficient of x is 2, indicating that for every unit increase in x, y increases by 2. Therefore, the rate of change for function A is 2.
For function B: y = 4x - 1, the coefficient of x is 4, indicating that for every unit increase in x, y increases by 4. Therefore, the rate of change for function B is 4.
Now, to find the difference in the rate of change between function A and function B, we subtract the rate of change of function B from the rate of change of function A:
Difference in rate of change = Rate of change of function A - Rate of change of function B
= 2 - 4
= -2
The difference in the rate of change between function A and function B is -2. This means that for every unit increase in x, function B increases at a rate that is 2 units greater than function A. It indicates that function B has a steeper slope and a faster rate of change compared to function A.
In summary, the difference in the rate of change between function A and function B is -2.
To know more about Function.
https://brainly.com/question/11624077
#SPJ8
Use brackets to make the following statement correct. 15 - 2 x 3 + 4 + 2 = 2.5
Answers
Let's add parenthesis inside the expression to make it true
\(\begin{gathered} (15-(2\times3+4))\div2=2.5 \\ \end{gathered}\)Let's solve the expression to check
\(\begin{gathered} (15-(2\times3+4))\div2 \\ (15-(6+4))\div2 \\ (15-10)\div2 \\ 5\div2 \\ 2.5 \end{gathered}\)
The distribution is symmetric. skewed. both symmetric and skewed.
Answers
The data distribution is skewed to the right. This is because the bars are clustered towards the left side of the histogram and taper off towards the right side.
The histogram of distances students live from school provided in the question shows that the majority of students in Tuan's homeroom live within a short distance of the school, with only a few students living farther away. The distribution is skewed to the right because the bars are clustered towards the left side of the histogram and taper off towards the right side. This indicates that there are fewer students who live farther away from school. A skewed distribution means that the data is not evenly distributed and tends to cluster towards one end. In this case, the distribution is skewed to the right because there are fewer students living farther away from school.
Learn more about histogram here: brainly.com/question/30354484
#SPJ4
Complete question is in the image attached below

Answer:
B. skewed.
Step-by-step explanation:
and then the next part is
1
hope this helps :)
I NEED HELP!! WILL GIVE BRAINLIEST
40 POINTS
1. For safety, a ladder should make a 75 degree angle with the ground, as shown here. Use a trigonometric ratio to determine how far up the wall a 16-foot ladder will reach. (Find x.) Round to four decimal places. (PICTURE IS INSERTED)
A. 4.1411 ft
B. 15.3802 ft
C. 15.4548 ft
D. 59.7128 ft
2. Use Pythagorean Theorem to find the length of segment AC (the distance the base of the ladder will be from the base of the house). Round to two decimal places.
A. 4.14 ft
B. 4.42 ft
C. 15. 45 ft
D. 73.27 ft

Answers
Answer:
I think it's A and C
Step-by-step explanation:
I could be wrong though
Answer:
c
Step-by-step explanation:
if not sorry
the product of two unit step functions in the s-domain (u(s)u(s)) is equivalent to what in the time domain?
Answers
The product of two unit step functions in the s-domain (u(s)u(s)) is equivalent to a ramp function in the time domain.
The unit step function u(t) is defined as 0 for t<0 and 1 for t≥0. When we take the Laplace transform of the unit step function, we get 1/s. Therefore, the product of two unit step functions can be written as:
u(t)u(t) = 1/s * 1/s
= 1/s²
Taking the inverse Laplace transform of 1/s² gives us a ramp function, which is defined as:
r(t) = t*u(t)
Therefore, the product of two unit step functions in the s-domain (u(s)u(s)) is equivalent to a ramp function in the time domain.
To know more about function,
https://brainly.com/question/28193995
#SPJ11
A manufacturer is contemplating the purchase of a punch press. Approximately 10,000 units are processed on the press each day and the machine efficiency is 95%. Assuming that each punching operation takes 10 s, determine how many pieces of the press must be purchased if the company operates two 8-h shifts/day. If the press in Exercise 10 has a scrap rate of 10%, would the answer to Exercise 10 change? Why or why not? Show calculations to support your answer. Assume that 70% of the "scrap" coming from the press in Exercise 10 can be reworked. Appropriately modify formula 2.1 and use it to determine the quantities of punch presses needer Is the new answer different from that obtained in Exercise 11? Explain.
Answers
To determine how many pieces of the press must be purchased, we need to consider the production rate, operating hours, efficiency, and scrap rate.
Number of units processed per day = 10,000
Machine efficiency = 95%
Punching operation time = 10 seconds
Number of shifts per day = 2
Number of hours per shift = 8
To calculate the required number of presses, we can use the following formula:
Number of presses = (Number of units processed per day / (Machine efficiency * Number of shifts * Number of hours)) * (Punching operation time / 3600)
Number of presses = (10,000 / (0.95 * 2 * 8)) * (10 / 3600) = 52.08
Therefore, approximately 52 presses would be needed to meet the production requirements.
If the press has a scrap rate of 10%, we need to consider the effect of scrapped units on the required number of presses.
Number of scrapped units per day = 10,000 * 0.10 = 1,000
Number of units that can be reworked = 1,000 * 0.70 = 700
To modify the formula for the new scenario, we subtract the reworked units from the total units processed per day:
Number of units processed per day (after rework) = 10,000 - 700 = 9,300
Number of presses (after considering scrap and rework) = (9,300 / (0.95 * 2 * 8)) * (10 / 3600) = 48.48
Therefore, approximately 48 presses would be needed when considering the scrap rate and rework capability.
The new answer is different from Exercise 11 because the scrap rate reduces the effective production rate, resulting in a lower requirement for punch presses. By accounting for scrap and rework, the company can optimize its resource allocation and production planning to meet the desired output while considering the potential loss due to scrap.
Learn more about accounting here:
https://brainly.com/question/5640110
#SPJ11
Pamela initially filled a measuring cup with 2/3 of a cup of syrup from a large jug. Then she poured 2/5 of a cup back into the jug. How much syrup remains in the measuring cup?
Answers
Answer:
I believe the answer is 4/15
Step-by-step explanation:
Write the equation of a line that is parallel to the line y=−4x+1 and goes through the point (2,0).
Answers
Answer:
y=-4x+8
Step-by-step explanation:
Hi there!
We are given the line y=-4x+1, and we want to write the equation of the line that is parallel to that line and that also passes through the point (2, 0)
Parallel lines have the same slope, so it makes sense to find the slope of the line y=-4x+1
The line is written in the format y=mx+b, where m is the slope and b is the y intercept.
As -4 is in the place of where m should be, the slope of the line is -4.
It's also the slope of the line parallel to it.
We can write the slope of the new line in slope-intercept form as well; this is the line so far, after substituting -4 as m:
y=-4x+b
Now we need to find b, which is the value of the y intercept
Remember that are given the point (2,0), which we can use to help solve for b; substitute 2 as x and 0 as y.
0=-4(2)+b
Multiply
0=-8+b
Add 8 to both sides
8=b
Substitute 8 as b into the equation:
y=-4x+8
Hope this helps!
If Leroy made 9 more penalty kicks than he missed how many penalty kicks did he make
Answers
The total number of penalty kicks is 9+ 2y where the penalties made is x and the penalties missed is y
How to determine how many penalty kicks he made?The given parameters are:
Leroy made 9 more penalty kicks than he missed
Represent the penalties made with x and the penalties missed with y
So, we have
x = 9 + y
The total number of penalty kicks is then calculated as
Total = x + y
This gives
Total = 9 + y + y
Evaluate
Total = 9+ 2y
Hence, the total number of penalty kicks is 9+ 2y where the penalties made is x and the penalties missed is y
Read more about equation at
https://brainly.com/question/148035
#SPJ1
What is the domain of the function represented by the graph?
10
- 10
-5
10
-10
O A. x>-3
B. X2-3
O C. x20
O D. x>0
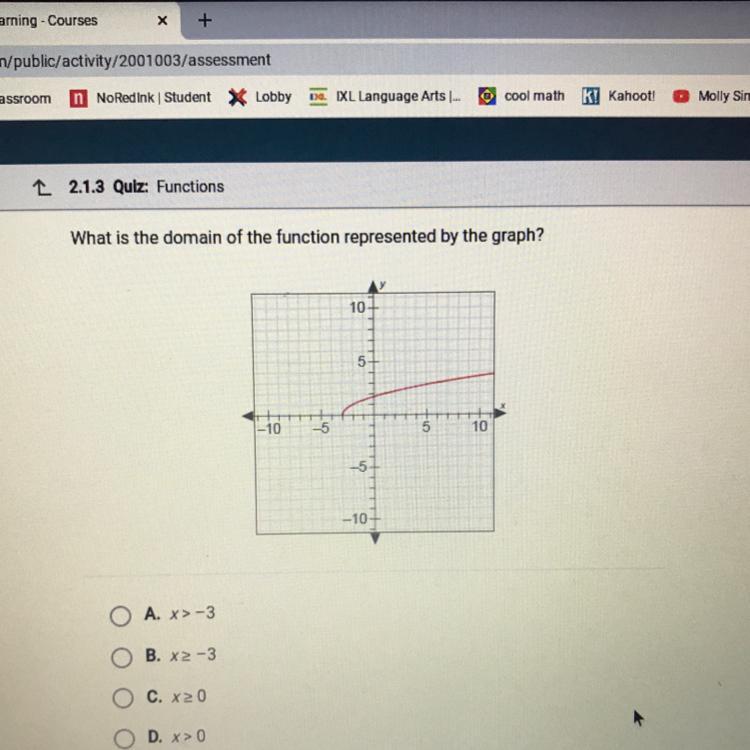
Answers
The red covers over -3 and beyond in the domain.
Answer
The correct answer is option B, \(x\geq 3\) such that a graph representing the function is given.
DomainThe domain of a function is the set of all the function's potential inputs.
How to find the domain of a function?We can see that the graph of the function originates from \((-3, 0)\) and goes in the direction of positive \(x-axis\).
So, the domain of the function is \(x\geq 3\).
Thus, the correct answer is option B \(x\geq 3\).
Learn more about domains here- https://brainly.com/question/13113489
#SPJ2
Please help fast! I have a 10 minutes :(

Answers
Maybe 11x? i dont really know, thats all the info we get
Question 1If a = 9 and b = 4, what is the value of 2a - b?A 10B 14 C 25D 72
Answers
To answer this question, we need to substitute the corresponding values of a and b in the respective algebraic expression, as follows:
a = 9, and b = 4
\(2a-b\Rightarrow2\cdot(9)-4=18-4=14\)Therefore, the value for the expression is 14 (option B).
the time spent waiting in the line is approximately normally distributed. the mean waiting time is 5 minutes and the variance of the waiting time is 1. find the probability that a person will wait for more than 6 minutes. round your answer to four decimal places.
Answers
There is a 30.85% chance that someone will have to wait longer than 6 minutes.
What is z score?Z score is used to determine by how many standard deviations the raw score is above or below the mean. It is given by:
The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the p-value, we get the probability that the value of the measure is greater than X.
z = (raw score - mean) / standard deviation
So,
We can write,
Mean of 6 minutes and variance = 1 minutes, hence:
Standard deviation = √variance = √1 = 1 minutes
For > 6 minutes:
z = (6 - 5)/2 = 1/2=0.5
P(z > 0.5) = 1 - P(z < 0.5)
P(z > 0.5) = 1 - 0.6915
P(z > 0.5) = 0.3085
Therefore,
There is a 30.85% chance that someone will have to wait longer than 6 minutes.
To learn more about information visit Decimal place :
brainly.com/question/23795454
#SPJ4
How do you write 3:5 in the ratio 1:n
Answers
Answer:
\(\frac{3}{5n}\)
Step-by-step explanation:
To write a polynomial in standard form, simplify and then arrange the terms in descending order.
ax²+bx+c
Rewrite the division as a fraction.
(3÷5)⋅1/n
Multiply 3÷5 by 1.
(3÷5)/n
Rewrite the division as a fraction. (3/5)/n
Multiply the numerator by the reciprocal of the denominator.
(3/5⋅(1/n)
Multiply 3/5 and 1/n.
3/5n
what is the answer to number 2 at the top?

Answers
The equation of the transformed exponential function g(x) is g(x) = 2^-x - 1
Writing an exponential function for the graph of g(x)From the question, we have the following parameters that can be used in our computation:
Parent function: y = 2^x
The graph of the transformed exponential function g(x) passes through the points (-2,3), (-1,1), (0,0), (1,-0.5) and (2, -0.75)
So, we have the following transformation steps:
1st Transformation:
Reflect y = 2^x across the y-axis
So, we have
y = 2^-x
2nd Transformation:
Translate y = 2^-x down by 1 unit
So, we have
y = 2^-x - 1
This means that
g(x) = 2^-x - 1
Hence, the equation of the function g(x) is g(x) = 2^-x - 1
Read more about transformation at
brainly.com/question/1548871
#SPJ1
claim sizes range between 0 and 1500. the probability that a claim is no greater than 500 is 0.8. claim sizes are uniformly distributed on (0; 500] and on (500; 1500]. calculate the expected claim sizes and its variance.
Answers
The expected claim size is 950 and the variance is 125000/9.
The probability that a claim is no greater than 500 is 0.8, which means the probability of a claim being greater than 500 is 0.2. The claim sizes are uniformly distributed on (0; 500] and on (500; 1500].
Therefore, the probability of a claim being in the range of (0; 500] is 0.8/2 = 0.4 and the probability of a claim being in the range of (500; 1500] is 0.2/2 = 0.1.
The expected claim size is calculated as the weighted average of the claim sizes in each range, where the weight is the probability of a claim being in that range. Thus, the expected claim size is (0.4 x 250 + 0.1 x 1000) = 950.
The variance of the claim size is calculated as the weighted average of the squared deviations from the expected claim size, where the weight is the probability of a claim being in that range. Thus, the variance is (0.4 x (250 - 950)^2 + 0.1 x (1000 - 950)^2) = 125000/9.
Therefore, the expected claim size is 950 and the variance is 125000/9.
For more questions like Probability click the link below:
https://brainly.com/question/30034780
#SPJ4
****
Identify the transformations that have been applied to the parent function
y=-1/(x-3)²-5.
Select all that apply.
Oshift 3 to the left
stretch
reflection over the x-axis
Oshift 5 up
Oshift 3 to the right
Oshift 5 down
O compression
Answers
Answer:
Step-by-step explanation:
The transformations that have been applied to the parent function y = 1/x^2 are:
shift 3 units to the right
shift 5 units down
reflection over the x-axis
So the correct options are:
shift 3 to the right
shift 5 down
reflection over the x-axis
prove or disprove: if and are subgroups of a group , then and is a subgroup of . what if is abelian?
Answers
G is abelian, then the argument is even simpler.
G is abelian, we have \((h_1k_1)(h_2k_2) = h_1h_2k_1k_2 = h_2h_1k_2k_1 = (h_2k_2)(h_1k_1)\),
HK is closed under the group operation.
The statement "if H and K are subgroups of a group G, then HK is a subgroup of G", we need to check if HK satisfies the three criteria for being a subgroup:
Closure under the group operation, the existence of an identity element, and the existence of inverse elements.
First, let's consider the case where G is not necessarily abelian.
HK is closed under the group operation, we need to show that for any \(h_1, h_2\) in H and \(k_1, k_2\) in K, the element \((h_1k_1)(h_2k_2)\) is also in HK.
The fact that H and K are subgroups to write \(h_1h_2\)in H and \(k_1k_2\) in K, and then use the associativity of the group operation to write\((h_1k_1)(h_2k_2) = h_1(h_2k_1)k_2\).
Since H and K are subgroups, \(h_2k_1\) is in HK, and therefore \((h_1k_1)(h_2k_2)\) is in HK.
Next, we need to show that HK has an identity element.
Since H and K are subgroups, they both contain the identity element of G, which we'll denote by e.
Then, for any h in H and k in K, we have \(h k e = h (k e) = h k\), which shows that HK contains the identity element.
HK has an inverse in HK. Let hk be an element of HK.
Since H and K are subgroups, \(\(h^{-1}\)\)is in H and \(k^{-1}\) is in K.
Then, \((hk)^{-1 }= k^{-1}h^{-1}\), which is in HK since H and K are subgroups.
H and K are subgroups of a group G, then HK is a subgroup of G, regardless of whether G is abelian or not. .
The identity element of HK is still the same as in the non-abelian case, and inverses can be computed as before.
H and K are subgroups of a group G, then HK is always a subgroup of G, regardless of whether G is abelian or not.
For similar questions on abelian
https://brainly.com/question/31330842
#SPJ11
Please help
For b: T=b/2-g
Answers
Answer:
Step-by-step explanation:
b/(2 - g) = T
(2 - g)(b/(2-g) = T)
b = T(2 - g)
What did he discover in the bath why was he so excited describe the discovery using geometric terms what do you predict he did next with his new discoveries need help with this !

Answers
What he discovered was a way to measure the volume of a solid, for when he entered the bath, the water rose, and the difference between heights was the volume.
The next he did was fill a bucket with water, measuring the height without the crowns, and the change in height when he deposited the crowns.
This difference is the volume. If the difference between those was not equal, then those were not made of the same materials.
She selects 150 trees at random from her orchard and uses this fertilizer on those trees and estimates the following regression: Y
^
i
=600+4.93X i
, where Y
^
i
denotes the predicted number of apricots obtained from the I th tree and X i
denotes the number of units of fertilizer used on the I th tree. A. H 0
:β 1
≥5.14 and H 1
:β 1
<5.14. B. H 0
:β 1
>4.93 and H 1
:β 1
≤4.93. C. H 0
:β 1
=5.14 and H 1
:β 1
=5.14. D. H 0
:β 0
=4.93 and H 1
:β 0
=4.93. Suppose the standard error of the estimated slope is 0.74. The t-statistic associated with the test Wendy wishes to conduct is (Round your answer to two decimal places. Enter a minus sign if your answer is negative.1
Answers
Given statement solution is :- The t-statistic associated with the test is approximately -0.28.
The t-statistic, which is used in statistics, measures how far a parameter's estimated value deviates from its hypothesised value relative to its standard error. Through the Student's t-test, it is utilised in hypothesis testing. In a t-test, the t-statistic is used to decide whether to accept or reject the null hypothesis.
To find the t-statistic associated with the test, we need to calculate the test statistic using the estimated slope coefficient, the null hypothesis, and the standard error.
The estimated slope coefficient is 4.93.
The null hypothesis is H₀: β₁ ≥ 5.14 (stating that the true slope coefficient is greater than or equal to 5.14).
The predicted slope's standard error is 0.74.
The formula to calculate the t-statistic is:
t = (estimated slope - hypothesized slope) / standard error
Plugging in the values:
t = (4.93 - 5.14) / 0.74
t = -0.21 / 0.74
t ≈ -0.28 (rounded to two decimal places)
Therefore, the t-statistic associated with the test is approximately -0.28.
For such more questions on t-statistic
https://brainly.com/question/28235817
#SPJ8