yo i’m stuck hahahelp ASAP -4 3/8 - (-1 1/4)
Answers
Answer:
I hope this helps
Step-by-step explanation:
-3 1/8
Related Questions
suppose s1, 1d is a critical point of a function f with contin- uous second derivatives. in each case, what can you say about f?
Answers
In each case, for a) f has local maximum at (1,1) and for b) f has saddle point at (1,1).
a) f_{xx}f_{yy}-(f_{xy})2
=(-4)(-2)-(1)2
=8-1
=7>0
f_{xx}=-4<0
Therefore, f has local maximum at (1,1)
b) f_{xx}f_{yy}-(f_{xy})2
=(-4)(-2)-(3)2
=8-9
=-1<0
Therefore, f has saddle point at (1,1)
A factor at which a feature of variables has partial derivatives identical to 0 however at which the feature has neither a most nor a minimal value.
To learn more about derivatives check the link below:
https://brainly.com/question/28376218
#SPJ4
Complete question:
Suppose (1, 1) is a critical point of a function f with continuous second derivatives. In each case, what can you say about f?a) f_{xx}f_{yy}-(f_{xy})2 and b) f_{xx}f_{yy}-(f_{xy})2
Diane sold some stuffs at a garage sale. She spent one-half of the money she made on a new bicycle. Next, she spent one-half of what was left on a portable stereo. If Diane had $40.00 left, how much money did she make from the garage sale
Answers
Answer:
$160
Step-by-step explanation:
Diane sold some stuffs at a garage sale.
Let the total value of the money Diane made = x
She spent one-half of the money she made on a new bicycle.
Amount spent on a Bicycle = 1/2 × x = 1/2x
Next,
Amount left
= x - 1/2x = 1/2x
She spent one-half of what was left on a portable stereo.
Amount spent spent on Portable stereo
= 1/2 × 1/2x
= 1/4x
If Diane had $40.00 left,
Hence:
The fraction of what was left is calculated as:
= x - (1/2x + 1/4x)
= x - (3/4x)
= 1/4x
Hence:
1/4x = $40
We can find the value of x now.
1/4 × x = $40
x/4 = $40
x = $40 × 4
x = $160
Therefore, the amount she made from the garage sale is $160
Answer:
Hey hey guys, it is 160.00
Step-by-step explanation:
What is the slope of the line that passes through the points below? (Enter your answer as a decimal if necessary.)

Answers
Answer:
5/4 should be your answer or in decimal form 1.25
Step-by-step explanation:
Slope is rise over run
Y2-Y1 divided by X2-X1
5/4
Marcia has a monthly income of $3,500. She budgets 8% for her cell phone. What amount does she budget for her cell phone, in dollars and cents
PLEASE HURRY I HAVE TIME LIMIT
Answers
Answer:
$280
Step-by-step explanation:
The area A of a trapezoid with parallel sides of lengths A andB and height H is a=1/2(a+b)h

Answers
Answer:
last option, 2A / (a + b) = h
Step-by-step explanation:

Answer:
\(\sf D)\ \dfrac{2A}{a+b}=h\ \ \textsf{or}\ \ 2A\div(a+b)=h\)
Step-by-step explanation:
Given: A = ½(a + b)h
We need to solve for h.
1. Rewrite the equation:
\(\sf A=\dfrac{1}{2}(a+b)h \implies A=\dfrac{1}{2}h(a+b)\)
2. Divide both sides by (a + b):
\(\sf \\\implies \dfrac{A}{a+b}=\dfrac{\dfrac{1}{2}h(a+b)}{a+b}\\\\\implies \dfrac{A}{a+b}=\dfrac{1}{2}h\)
3. Multiply both sides by 2:
\(\sf \\\implies 2\left(\dfrac{A}{a+b}\right)=2\left(\dfrac{1}{2}h\right)\\\\\implies \dfrac{2A}{a+b}=h\ \ \textsf{or}\ \ 2A\div(a+b)=h\)
Think of all the reasonable outcomes of X. How many possible outcomes does X have?
O Too many to list
O 18 O 19 O unknown
Answers
The number of possible outcomes of X, where X represents the result of throwing three dice simultaneously, is 6³ = 216. (D)
This is because each die has 6 possible outcomes: 1, 2, 3, 4, 5, or 6. When three dice are thrown, the outcome for each die is determined independently, so the total number of possible combinations of outcomes is 6 x 6 x 6³ = 6 = 216. (D)
Each of these 216 combinations represents a different outcome of X. To determine the outcome of X, we need to know the outcome for each of the three dice.
For example, if the outcome for the first die is 3, the second die is 4, and the third die is 5, then the outcome of X would be (3, 4, 5). There are 216 possible outcomes of X because there are 6 possible outcomes for each of the three dice, and each combination of outcomes represents a different result.
To know more about possible outcomes click on below link:
https://brainly.com/question/19567251#
#SPJ11
Complete question :
if 3 dices are thrown simultaneously and let that event is called as X then Think of all the reasonable outcomes of X. How many possible outcomes does X have?
A Too many to list
B 18
C 19
D 216
What is the sum of the polynomials? (6x+7+8^2) + (2x^2-3)
Answers
Answer:
2(x^2 + 3x + 34)
Step-by-step explanation:
(6x+7+8^2) + (2x^2-3)
= 6x + 7 + 64 + 2x^2 - 3
= 2x^2 + 6x + 68
= 2(x^2 + 3x + 34)
(20 POINTS) Joseph buys a subway pass for $55. Every time he rides the subway, money is deducted from the value of the pass. He rode the subway 5 times and $40 was deducted from the value of the pass. How much was deducted from Joseph's account for each ticket? Write a mathematical expression to represent this situation; then find the answer.
Answers
The amount deducted from Joseph's account for each ticket is $8
The amount deducted from Joseph's account for each ticket?Total cost of subway pass Joseph bought = $55Number of times he rode the subway = 5Total amount deducted from the value of the subway pass = $40The amount deducted from Joseph's account for each ticket = Total amount deducted from the value of the subway pass ÷ Number of times he rode the subway
= $40 / 5
= $8 per ticket
Total amount remaining in the subway pass = Total cost of subway pass Joseph bought - Total amount deducted from the value of the subway pass
y = $55 - $40
= $15
The mathematical equation to represent this situation is y = $55 - $40
Read more about equation:
https://brainly.com/question/4344214
#SPJ1
A large right triangle is going to be a part

Answers
The given triangle in the question is a right-angled triangle. In order to get the length of each side, we will apply the Pythagoras theorem.
The Pythagoras theorem is,
\(\text{Hypotenuse}^2=Opposite^2+Adjacent^2\)Where,
\(\begin{gathered} \text{Hypotenuse}=5 \\ \text{Opposite}=2x-2 \\ \text{Adjacent}=x \end{gathered}\)Therefore,
\(5^2=(2x-2)^2+x^2\)Let us expand the above
\(\begin{gathered} 25=2x(2x-2)-2(2x-2)+x^2 \\ 25=4x^2-4x-4x+4+x^2 \\ 25=5x^2-8x+4 \end{gathered}\)Switch sides
\(5x^2-8x+4=25\)Subtract 25 from both sides
\(5x^2-8x+4-25=25-25\)Simplify
\(5x^2-8x-21=0\)Solve with the quadratic formula
\(x_{1,\: 2}=\frac{-\left(-8\right)\pm\sqrt{\left(-8\right)^2-4\cdot\:5\left(-21\right)}}{2\cdot\:5}\)Thus
\(\sqrt[]{(-8)^2-4\cdot\: 5(-21)}=22\)Therefore,
\(x_{1,\: 2}=\frac{-\left(-8\right)\pm\:22}{2\cdot\:5}\)Separate the solutions
\(x_1=\frac{-\left(-8\right)+22}{2\cdot\:5},\: x_2=\frac{-\left(-8\right)-22}{2\cdot\:5}\)Hence,
\(\begin{gathered} x=\frac{-(-8)+22}{2\cdot\: 5}=3 \\ x=\frac{-(-8)-22}{2\cdot\: 5}=-\frac{7}{5} \end{gathered}\)The solutions to the quadratic equations are
\(x=3,\: x=-\frac{7}{5}\)Therefore, from the above result, the length of a triangle can never be negative.
Hence, x = 3
Let us now solve the length of the remaining side
\(\begin{gathered} 2x-2=2(3)-2=6-2=4 \\ \therefore2x-2=4 \end{gathered}\)Therefore, the length of each leg is
\(3ft,4ft,5ft\)A factory produces bicycles at a rate of 95 + 588t2 – 14t bicycles per week (t in weeks). How many bicycles were produced from the beginning of week 2 to the end of week 3? (Give your answer as a whole or exact number.) number of bicycles:
Answers
The bicycles produced from the beginning of week 2 to the end of week 3 are 2926.
To find the number of bicycles produced from the beginning of week 2 to the end of week 3, we will use the given production function P(t) = 95 + 588t^2 - 14t, where t is the number of weeks.
First, we need to find the number of bicycles produced by the end of week 2 and week 3.
To do this, we'll plug in t = 2 and t = 3 into the production function:
P(2) = 95 + \(588(2)^{2}\) - 14(2) = 95 + 588(4) - 28 = 95 + 2352 - 28 = 2419 bicycles
P(3) = 95 + \(588(3)^{2}\) - 14(3) = 95 + 588(9) - 42 = 95 + 5292 - 42 = 5345 bicycles
Now we need to find the difference between the bicycles produced by the end of week 3 and those produced by the end of week 2:
Number of bicycles produced from the beginning of week 2 to the end of week 3 = P(3) - P(2) = 5345 - 2419 = 2926 bicycles
So, the factory produced 2926 bicycles from the beginning of week 2 to the end of week 3.
Know more about Production function here:
https://brainly.com/question/31429707
#SPJ11
in lixue’s garden, the green pepper plants grew 5 inches in 3 4 month. at this rate, how many feet can they grow in one month? (let 5 inches
Answers
It would grow by approximately 1.6668 inches to 1.2504 inches
In Lixue's garden, the green pepper plants grew 5 inches in 3-4 months. To find out how many feet they can grow in one month, we can use the given information.
Let's start by converting the inches to feet. Since there are 12 inches in a foot, we divide 5 inches by 12 to get the equivalent in feet: 5 inches ÷ 12 = 0.4167 feet (rounded to four decimal places).
Now, we need to determine how much they can grow in one month. Since the plants grew 0.4167 feet in 3-4 months, we divide this amount by the number of months to find their average monthly growth.
If we assume that the plants grew 0.4167 feet in 3 months, their monthly growth rate would be 0.4167 feet ÷ 3 months = 0.1389 feet per month (rounded to four decimal places).
If we assume that the plants grew 0.4167 feet in 4 months, their monthly growth rate would be 0.4167 feet ÷ 4 months = 0.1042 feet per month (rounded to four decimal places).
Therefore, based on the given information, the green pepper plants can grow approximately 0.1389 feet to 0.1042 feet in one month, depending on whether we consider a 3-month or 4-month timeframe.
Another question on the Growth of Plant: https://brainly.com/question/12220885
#SPJ11
if p = 2^k + 1 is prime, show that every quadratic nonresidue of p is a primitive root of p.
Answers
Every quadratic nonresidue of p is a primitive root of p, when p = 2^k + 1 is primeIf p = 2^k + 1 is a prime number, we want to show that every quadratic nonresidue of p is a primitive root of p.
In other words, we aim to prove that if an element x is a quadratic nonresidue modulo p, then it is also a primitive root of p.
Let's assume p = 2^k + 1 is a prime number. To prove that every quadratic nonresidue of p is a primitive root of p, we can use the properties of quadratic residues and quadratic nonresidues.
A quadratic residue modulo p is an element y such that y^((p-1)/2) ≡ 1 (mod p), while a quadratic nonresidue is an element x such that x^((p-1)/2) ≡ -1 (mod p).
Now, let's consider an element x that is a quadratic nonresidue modulo p. We want to show that x is a primitive root of p.
Since x is a quadratic nonresidue, we know that x^((p-1)/2) ≡ -1 (mod p). By Euler's criterion, this implies that x^((p-1)/2) ≡ -1^((p-1)/2) ≡ -1^2 ≡ 1 (mod p).
Since x^((p-1)/2) ≡ 1 (mod p), we can conclude that the order of x modulo p is at least (p-1)/2. However, since p = 2^k + 1 is a prime, the order of x modulo p must be equal to (p-1)/2.
By definition, a primitive root of p has an order of (p-1). Since the order of x modulo p is (p-1)/2, it follows that x is a primitive root of p.
Learn more about Euler's criterion here:
brainly.com/question/12977984
#SPJ11
FP!!!!!!!!!!!!!!!
What is (10 x 10 ) + 50 + 1 =
Answers
look at the attached picture
Hope it will help you

Answer:
((2•5x10) + 50) + 1
10x10 + 51 =
Answer: 151 :)
m
6 cm
NET OF TOY BOX
15 cm
at is the surface area, in square centimeters, image attached

Answers
The total surface area of the toy box using the net is 390 square cm
Calculating the total surface area using the net.From the question, we have the following parameters that can be used in our computation:
The net of the toy box
The surface area of the toy box from the net is calculated as
Surface area = sum of areas of individual shapes that make up the net of the toy box
Using the above as a guide, we have the following:
Area = 2 * 5 * 6 + 2 * 5 * 15 + 2 * 6 * 15
Evaluate
Area = 390
Hence, the surface area is 390 square cm
Read more about surface area at
brainly.com/question/26403859
#SPJ1
The circumference of a circle is 9.62cm.
Find the length of the diameter.
Give your answer rounded to 2 DP.
Answers
Answer:
3.06cm
Step-by-step explanation:
⁄(⁄ ⁄•⁄ω⁄•⁄ ⁄)⁄⁄(⁄ ⁄•⁄ω⁄•⁄ ⁄)⁄
Answer:3.06cm
Step-by-step explanation:
I WILL GIVE
Create an equivalent expression for this

Answers
Answer: C
Step-by-step explanation:
Answer: I think the answer is A.
Step-by-step explanation:

Find the minimum sample size needed (n) to estimate the mean monthly earnings of students at Norco college. We want 95% confidence that we are within a margin of error of $150 when the population standard deviation is known to be $625 (o = 625).
Answers
To estimate the mean monthly earnings of students at Norco College with a 95% confidence level and a margin of error of $150, a minimum sample size of 61 students is required.
To find the minimum sample size needed (n) to estimate the mean monthly earnings of students at Norco College with a 95% confidence level and a margin of error of $150, we can use the formula:
n = (Z * o / ME)^2
where Z is the Z-score corresponding to the desired confidence level, o is the population standard deviation, and ME is the margin of error.
Given the information:
Confidence level = 95%
Margin of error (ME) = $150
Population standard deviation (o) = $625
First, we need to find the Z-score corresponding to a 95% confidence level. The Z-score for a 95% confidence level is approximately 1.96.
n = (1.96 * 625 / 150)^2
= (1.96 * 4.1667)^2
≈ 7.7532^2
≈ 60.05
The minimum sample size needed (n) is approximately 60.05. Since we cannot have a fraction of a person, we would round up to the nearest whole number. Therefore, the minimum sample size needed is 61.
Learn more about standard deviation here:
https://brainly.com/question/23907081
#SPJ11
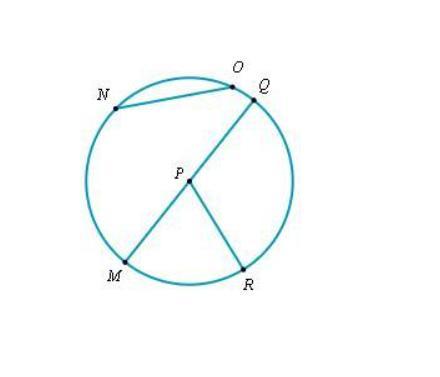
A circle with center is shown in the figure below.
S
T
W
R
U
V
(a) Name a radius:
(b) Name a diameter:
(c) Name a chord:
(d) If the length of is units,
what is the length of ?
Answers
The names of the radius , chord and diameter of a circle are as follow,
Radius of the circle are PQ, PM , And PR.
Diameter of the circle is QM
Chord of the circle is ON.
Length of QM in the circle = 4units.
In the attached figure of the circle,
Center of the circle is P.
radius of the circle is a distance from the center of the circle to its circumference.
Radius = PQ, PM , And PR.
Diameter of the circle passing through center P is QM.
Chord of the circle representing a line segment having endpoints on the circumference of the circle.
Chords are ON and MQ.
Diameter is the longest chord.
length of PR is 2 units,
PR is radius
QM is diameter
QM = 2(PR)
length of QM = 2(2)
= 4 units.
Therefore, for the given circle we have,
Radius are PQ, PM , And PR.
Diameter is QM
Chord is ON.
Length of QM = 4units.
learn more about circle here
brainly.com/question/28998766
#SPJ1
The above question is incomplete, the complete question is:
A circle with center P is shown in the figure below.
(a) Name a diameter:
(b) Name a radius:
(c) Name a chord:
(d) If the length of PR is 2 units, what is the length of QM
Attached figure.
(3x^3-x+4) +(x^2-5x-5)
Answers

what does x-26= x2 equal ?
Answers
Answer:
X= 13
Step-by-step explanation:
to go to a movie, a family with 2 adults and 4 children spends 64.00. a family containing 1 adult and 3 children spends 42.00. find the cost of an adult movie ticket and the cost of a child movie ticket
Answers
Answer: The cost of a ticket for an adult is $12 while for children it is $10.
Step-by-step explanation:
Let's assume that cost for adults is A while for children it is C
Now,
2 adults and 4 children spend $64.
2A + 4C = 64
1 adult and 3 children spend $42.
A + 3C = 42
Multiply by 2
2A + 6C = 84
By subtracting equations
6C - 4C = 84 - 64
2C = 20
C = 10
A = 42 - 3(10)
A = 12
Hence "The cost of a ticket for an adult is $12 while for children it is $10".
us
Find the point-slope equation for
the line that passes through the
points (-6, 24) and (5, -31). Use
the first point in your equation.

Answers
Answer:
first box is 24
second is -5
third is -6
Step-by-step explanation:
Exercise 10
You randomly choose one of the tiles. Without replacing the first tile, you choose a second tile. What is the probability of the compound event? Write your answer as a fraction or percent rounded to the nearest tenth.

Answers
The probability of choosing a 5 and then a 6 is 1/49
Finding the probability of the compound eventFrom the question, we have the following parameters that can be used in our computation:
The tiles
Where we have
Total = 7
The probability of choosing a 5 and then a 6 is
P = P(5) * P(6)
So, we have
P = 1/7 * 1/7
Evaluate
P = 1/49
Hence, the probability of choosing a 5 and then a 6 is 1/49
Read more about probability at
https://brainly.com/question/31649379
#SPJ1
Question
You randomly choose one of the tiles. Without replacing the first tile, you choose a second tile. Find the probability of the compound event. Write your answer as a fraction or percent rounded to the nearest tenth. The probability of choosing a 5 and then a 6
two office aids at lake norman high school are responsible for getting the daily tardy list to the appropriate principals by 3:00pm each day. livi works on the lists 30% of the days and caitlyn works on the tardy lists 70% of the days. livi gets the lists to the correct principals in time 90% of the time. caitlyn gets the tardy lists to the correct principals 92% of the time. if mr. gentle sees that the tardy list is on time, what is the probability that today livi is responsible for the list?
Answers
The probability that Livi is responsible for the list today, given that it is on time, is approximately 0.2959 or 29.59%.
To calculate the probability that today Livi is responsible for the list given that it is on time, we can use Bayes' theorem.
Let's define the events
A: Livi is responsible for the list
B: The list is on time
We are given
P(A) = 0.3 (Livi works on the lists 30% of the days)
P(B|A) = 0.9 (Livi gets the lists to the correct principals in time 90% of the time)
P(B|not A) = 0.92 (Caitlyn gets the tardy lists to the correct principals 92% of the time)
We want to calculate
P(A|B) (The probability that Livi is responsible for the list given that it is on time)
By Bayes' theorem
P(A|B) = (P(A) * P(B|A)) / [P(A) * P(B|A) + P(not A) * P(B|not A)]
Substituting the given values:
P(A|B) = (0.3 * 0.9) / [0.3 * 0.9 + (1 - 0.3) * 0.92]
P(A|B) = 0.27 / (0.27 + 0.7 * 0.92)
P(A|B) = 0.27 / (0.27 + 0.644)
P(A|B) = 0.27 / 0.914
P(A|B) ≈ 0.2959
Therefore, the probability that today Livi is responsible is approximately 0.2959 or 29.59%.
To know more about Probability:
brainly.com/question/32117953
#SPJ4
AXYZ has side lengths that measure 20 centimeters each. Which of the
following best describes this type of triangle?
A. Scalene triangle
B. Right triangle
C. Obtuse triangle
D. Equilateral triangle

Answers
Step-by-step explanation:
The triangle is equilateral (OPTION D) because any triangle that has 3 equal side lengths is an equilateral triangle.
Show that if {a_n} converges to L and if a_n ≤ L for infinitely many values of n, then there is a subsequence of {a_n} that is increasing and converges to L.
Answers
We have shown that if {a_n} converges to L and if a_n ≤ L for infinitely many values of n, then there exists a subsequence {a_nk} of {a_n} that is increasing and converges to L.
To show that if {a_n} converges to L and if a_n ≤ L for infinitely many values of n, then there is a subsequence of {a_n} that is increasing and converges to L, we can proceed as follows:
Since {a_n} converges to L, for any ε > 0, there exists an integer N such that for all n ≥ N, |a_n - L| < ε. This means that eventually, all terms of {a_n} will be arbitrarily close to L.
Now, let's consider the subsequence {a_nk}, where n1 < n2 < n3 < ... is an increasing sequence of indices such that a_nk ≤ L for each k.
Since a_nk ≤ L for infinitely many values of k, we can construct the subsequence {a_nk} as follows:
Choose n1 such that a_n1 ≤ L.
Choose n2 such that n2 > n1 and a_n2 ≤ L.
Choose n3 such that n3 > n2 and a_n3 ≤ L.
And so on.
By construction, the subsequence {a_nk} is increasing because the indices n1, n2, n3, ... are increasing.
Now, we need to show that {a_nk} converges to L. Given ε > 0, since {a_n} converges to L, there exists an integer N' such that for all n ≥ N', |a_n - L| < ε.
Since {a_n} is a sequence of indices, we can choose N = max{N', n1, n2, n3, ...}. Then, for all k ≥ N, we have n_k ≥ N. Therefore, for all k ≥ N, |a_nk - L| < ε.
This shows that the subsequence {a_nk} converges to L.
In summary, we have shown that if {a_n} converges to L and if a_n ≤ L for infinitely many values of n, then there exists a subsequence {a_nk} of {a_n} that is increasing and converges to L.
for such more question on converges
https://brainly.com/question/17236753
#SPJ8
You are studying the impacts of rising sea levels on an estuary, and are modeling how the salinity of a particular area changes with the tidal cycle. The mixed-tide cycle on this part of the coast has a period of approximately 25 hours, giving the salinity fluctuation of the estuary a similar cycle. Twenty years ago, the salinity was modeled by the functions (t) = 12 sin(t) cos(t) +15, where t is in hours and s (t) is the salinity in parts per million (ppm). But you have determined that the model S (t) = 14 sin(t) cos(t) + 17 more closely fits the current data. SHE • Graph both s (t) and S (t) using technology. What do you observe about the two functions? How are they the same? How are they different? . Find both s' (t) and S' (t), describing what differentiation rules you use for each, and showing your process. • Use technology to determine the values of t for which s' (t) and S' (t) have horizontal tangents. (Focus on the first period of the graphs, so t < 25.) • What do you notice about the t values for which the two derivatives have horizontal tangents? • Use these t values, and the graphs of the two salinity functions, to determine the highest and lowest salinity for the estuary using the historical model, and using the current model. - What do you notice? • How does this relate to what you are studying? • Use technology to find the t value for which the concentration of salinity is most rapidly increasing in both models. What is the greatest increase rate in each model? What are the units on the increase rates? • What do you observe about these two increase rates?
Answers
The given models to study the fluctuation of salinity of an estuary are: S(t) = 12 sin(t) cos(t) +15 (twenty years ago)S(t) = 14 sin(t) cos(t) + 17 (current data). To graph the two functions, we use a calculator or a graphing tool. We can use Desmos calculator to graph both functions. The graphs of both functions are shown below:
Graph of the first function: Graph of the second function: Comparing the two functions, we can notice that they are almost identical, except that the current model is slightly shifted upwards by 2 and its amplitude is 2 higher. So, the two functions are the same in that they both have the same shape, and they differ in their amplitude and vertical shift. Since the horizontal axis is in hours, both functions have a period of 25 hours. They repeat their shape after every 25 hours.
Differentiating S(t) and s(t):Differentiating the given function S(t) = 14 sin(t) cos(t) + 17 using the product rule,
we getS'(t) = 14(cos^2(t) - sin^2(t))Differentiating the given function s(t) = 12 sin(t) cos(t) + 15 using the product rule, we get: s'(t) = 6 cos(2t).
Now, we will find the values of t for which s'(t) and S'(t) have horizontal tangents by setting the derivatives equal to zero and solving for t:S'(t) = 14(cos^2(t) - sin^2(t)) = 0or cos^2(t) - sin^2(t) = 0or cos(2t) = 0t = (nπ + π/4), where n is an integer.s'(t) = 6 cos(2t) = 0t = nπ/4, where n is an integer.Now, let's determine the highest and lowest salinity for the estuary using the historical model and the current model. We can notice that both functions have the same maximum value of 29 parts per million (ppm) and minimum value of 1 ppm.
Relation to what we are studying:
We are studying the impacts of rising sea levels on an estuary and modeling how the salinity of a particular area changes with the tidal cycle. By comparing the salinity values obtained from the historical model and the current model, we can observe how the salinity of the estuary has changed over time. This helps us understand the effects of rising sea levels and how they affect the estuary's ecosystem. T value for which the concentration of salinity is most rapidly increasing:
To find the t value for which the concentration of salinity is most rapidly increasing in both models, we differentiate both functions again. Differentiating S'(t), we get:S''(t) = -28sin(2t)Differentiating s'(t), we get:s''(t) = -12 sin(2t)Using a graphing tool, we can observe that the concentration of salinity is most rapidly increasing when t = nπ/2, where n is an odd integer. Thus, the greatest increase rate in both models is 28 ppm/hr. The units on the increase rates are parts per million per hour (ppm/hr).
In this question, we studied the impacts of rising sea levels on an estuary and modeled how the salinity of a particular area changes with the tidal cycle. We observed that the historical model and the current model have the same shape but differ in their amplitude and vertical shift. We also found the t values for which the derivatives have horizontal tangents and determined the highest and lowest salinity for the estuary using both models. We observed that both models have the same maximum and minimum values. We then related this to what we are studying and observed how the changes in salinity help us understand the effects of rising sea levels on the estuary's ecosystem. Finally, we found the t value for which the concentration of salinity is most rapidly increasing in both models and observed that the greatest increase rate in both models is 28 ppm/hr.
To know more about horizontal tangents :
brainly.com/question/30175066
#SPJ11
WILL GIVE BRAINLEST ANSWER IF DONE IN 24 HRS Two forces with magnitudes of 150 and 100 pounds act on an object at angles of 40° and 170°, respectively. Find the direction and magnitude of the resultant force. Round to two decimal places in all intermediate steps and in your final answer. (pls show work)
Answers
Answer:
114.96 pounds at angle 81.76°
Step-by-step explanation:
Let i be the component along x-axis and j be the component along y-axis.
First force that is given is 150 acting at angle 40; \(F1 = 150cos170i + 150sin40j = 114.91i +96.42j\)
The second force 100 is acting at angle 170;
\(F2 = 100cos170i + 100sin170j = -98.48i + 17.36j\)
We now have the resultant force, which is: \(114.91i + 96.42j + (-98.48i + 17.36j) = 16.43i + 113.78j\)
Magnitude of resultant:
\(\sqrt{16.43^{2} + 113.78^{2} }\) = 114.96 pounds
Angle it makes with horizontal; inverse tangent of \(\frac{(113.78)}{(16.43)}\) = 81.76 degrees
Hope this helps; Brainliest appreciated!
This equation has one solution. 5(x – 1) 3x = 7(x 1) what is the solution?
Answers
Answer:
send the complete question . there are some missing signs .
Compute the truth table for --P<->Q and label each row. Be sure to use canonical form. (For an answer, e.g., you can write Tor true.) Row 1: Row 2: Row 3: Row 4:
Answers
To compute the truth table for --P<->Q, we need to first understand the meaning of the logical operator "<->". This operator stands for "if and only if" and it is true only when both statements are either true or false.
In other words, if P is true and Q is true or if P is false and Q is false, then the statement is true. If P is true and Q is false or if P is false and Q is true, then the statement is false.
Using canonical form, we can write the statement --P<->Q as (P v ~Q) ^ (~P v Q), where ^ stands for "and" and v stands for "or". The negation of P is represented by ~P.
Now, we can construct the truth table with the four possible combinations of truth values for P and Q. Labeling each row from 1 to 4, we have:
Row 1: P is true, Q is true
Row 2: P is true, Q is false
Row 3: P is false, Q is true
Row 4: P is false, Q is false
Next, we evaluate the canonical form for each row. For example, in row 1, we have (true v ~true) ^ (~true v true), which simplifies to true ^ true, resulting in a truth value of true. Continuing this process for all four rows, we get:
Row 1: true
Row 2: false
Row 3: false
Row 4: true
Therefore, the truth table for --P<->Q using canonical form is:
| P | Q | --P<->Q |
|---|---|---------|
| T | T | T |
| T | F | F |
| F | T | F |
| F | F | T |
The first column represents the truth values for P, the second column represents the truth values for Q, and the third column represents the truth values for --P<->Q. The answer is more than 100 words and includes the requested term "canonical form".
To know more about Truth Table visit :
https://brainly.com/question/31482105
#SPJ11