Yesterday, two friends went into a bank to open savings accounts. Megan started by putting $80 in her account, and she will deposit an additional $15 each week. Noah made no initial deposit, but he will add $25 more each week. In a few weeks, the friends will have the same account balance.
Answers
Answer:
8 weeks
Step-by-step explanation:
We are to find the number of weeks that they will have the same account balance.
Let the number of weeks be x.
Megan started by putting $80 in her account, and she will deposit an additional $15 each week. This means after x weeks, she will have:
80 + 15x
Noah made no initial deposit, but he will add $25 more each week. After x weeks, he will have:
25x
To find the number of weeks for their amounts to be the same, we equate their amounts to one another:
80 + 15x = 25x
Collexting like terms and solving for x:
80 = 25x - 15x
80 = 10x
=> x = 80 / 10 = 8 weeks
After 8 weeks, the money in their accounts will be the same.
Related Questions
I will give you cookie if it’s right

Answers
Answer:
The slope is just 1.
Step-by-step explanation:
Rise 1, up 1. so 1 over 1 just equals 1
This question please
Answers
Answer:
Wht question. don't see nothing
is { 20, 40, 60, 80....} infinite or finite
Answers
The sequence {20, 40, 60, 80, ...} is an infinite sequence.
To determine whether a sequence is finite or infinite, we need to examine if there is a clear pattern or rule that allows us to generate more terms indefinitely.
In this case, we can observe that each term in the sequence is obtained by multiplying the previous term by 2. Starting with 20, we multiply by 2 to get 40, then multiply by 2 again to get 80, and so on. This pattern continues indefinitely, with each term being twice the previous term.
Since there is a clear rule to generate more terms and there is no specific endpoint or limit, the sequence is infinite. We can continue generating terms by multiplying the last term by 2 repeatedly, resulting in an unending sequence of numbers.
It's important to note that even though we haven't listed out all the terms, we can still confidently conclude that the sequence is infinite based on the established pattern and rule.
For more such question on sequence visit:
https://brainly.com/question/7882626
#SPJ8
What value of b^2 is needed for there to be exactly one real solution of a quadratic equation? Explain.
Answers
Answer:
4ac
Step-by-step explanation:
Assuming you're referring to the equation \(ax^2+bx+c=0\).
Since the discriminant \(D=b^2-4ac\) has to be equal to 0 in order for there to be exactly one real solution, then we have the following:
\(0=b^2-4ac\\b^2=4ac\)
Therefore, b² needs to be the same value as 4ac.
Find the value of b for this line
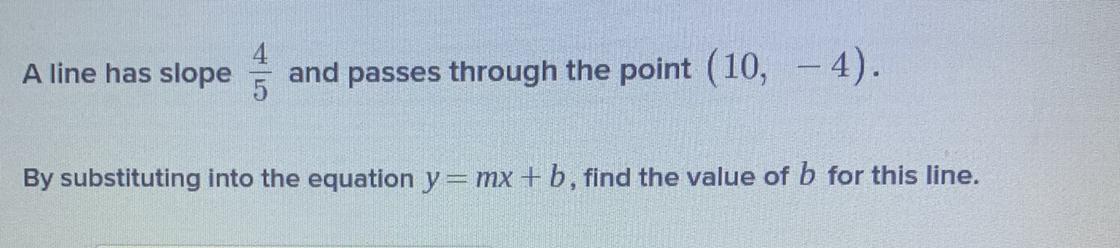
Answers
Answer:
b = - 12
Step-by-step explanation:
substituting m = \(\frac{4}{5}\) , x = 10, y = - 4 into y = mx + b , gives
- 4 = (\(\frac{4}{5}\) × 10) + b
- 4 = (4 × 2) + b
- 4 = 8 + b ( subtract 8 from both sides )
- 12 = b
Peggy earned $20 for each lawn she mowed last summer. This summer, she raised her price to $23 per lawn. What is the percent increase of Peggy’s charges?

Answers
Answer:
15 percent
Step-by-step explanation: You will substract the new value from the old value.
23-20
Now you will get the difference between them and divide that by the original amount.
3/20
This will equal 0.15 in which you now multiply by 100
15 percent
1. (25 pts.) A simple roof supports are being built using only the sizes of round dowel stock shown in the table. Roof supports are to be made of Black Locust. Proposed roof has an area of 600 ft2. This design is for compressive failure, not yield, Su-N[10.18, 0.4) ksi. The design is for a static snow load of F - N[100, 15] lb/ft2. There are four supports to the roof. Assume an evenly distributed axial load on roof supports, no bending, no buckling. a. (4 pts) Give the load data for one roof support (fill in the blanks): P-N ] kip b. (4 pts) What is the value of z that corresponds to a reliability of 0.995 against compressive failure? c. (4 pts) What is the design factor associated with a reliability of 0.995 against compressive failure? d. (4 pts) What diameter dowel is needed for a reliability of 0.995? e. (4 pts) What size of standard dowel is needed for a minimum reliability of 0.995 against failure? Standard Diameter 4 4.5 5 6 7 8 (inches) f. (5 pts) What is the actual factor of safety?
Answers
The actual factor of safety is 0.0874. a) One roof support load data: P = (600 × 100) / 4 = 150000 N
b) The value of z that corresponds to a reliability of 0.995 against compressive failure is 2.81.
c) The design factor associated with a reliability of 0.995 against compressive failure is 3.15.
d) The required diameter dowel for a reliability of 0.995 is calculated by:
\[d = \sqrt{\frac{4P}{\pi Su N_{d}}}\]
Where, \[Su\]-N[10.18, 0.4) ksi\[N_{d}\]= 0.2\[d
= \sqrt{\frac{4(150000)}{\pi (10.18) (0.2)}}
= 1.63 \,inches\]
The diameter of the dowel needed for a reliability of 0.995 is 1.63 inches.
e) A standard dowel with a diameter of at least 1.63 inches is required for a minimum reliability of 0.995 against failure. From the standard diameters given in the question, a 6-inch diameter dowel is the most suitable.
f) The actual factor of safety is the load that will cause the dowel to fail divided by the actual load. The load that will cause the dowel to fail is
\[P_{f} = \pi d^{2} Su N_{d}/4\].
Using the value of d = 1.63 inches,
\[P_{f} = \frac{\pi (1.63)^{2} (10.18) (0.2)}{4}
= 13110.35 \, N\]
The actual factor of safety is: \[\frac{P_{f}}{P} = \frac{13110.35}{150000} = 0.0874\]
Therefore, the actual factor of safety is 0.0874.
To know more about support load data visit:
https://brainly.com/question/25762649
#SPJ11
Short answer please ASAP

Answers
The lateral surface area of the rectangular prism given in the picture is 36 cm ²
How to find the lateral surface area of a rectangular prism ?The lateral surface area of a rectangular prism can be found by the formula :
= 2 x height x ( Length + Breadth )
Height = 2 cm
Length = 3 cm
Breadth = 6 cm
The lateral surface area is therefore:
= 2 x 2 x ( 3 + 6 )
= 4 x 9
= 36 cm ²
In conclusion, the lateral surface area is 36 cm ².
Find out more on lateral surface area at https://brainly.com/question/14642720
#SPJ1
y=x+7 linear or nonlinear? ASAP please
Answers
Answer:
linear
Step-by-step explanation:
the exponent of x is 1, so the function intercepts the x axis only one time
Ch. 9 lesson 3 skills practice area of trapezoids
Use formula A= 1/2 h (b1 + b2
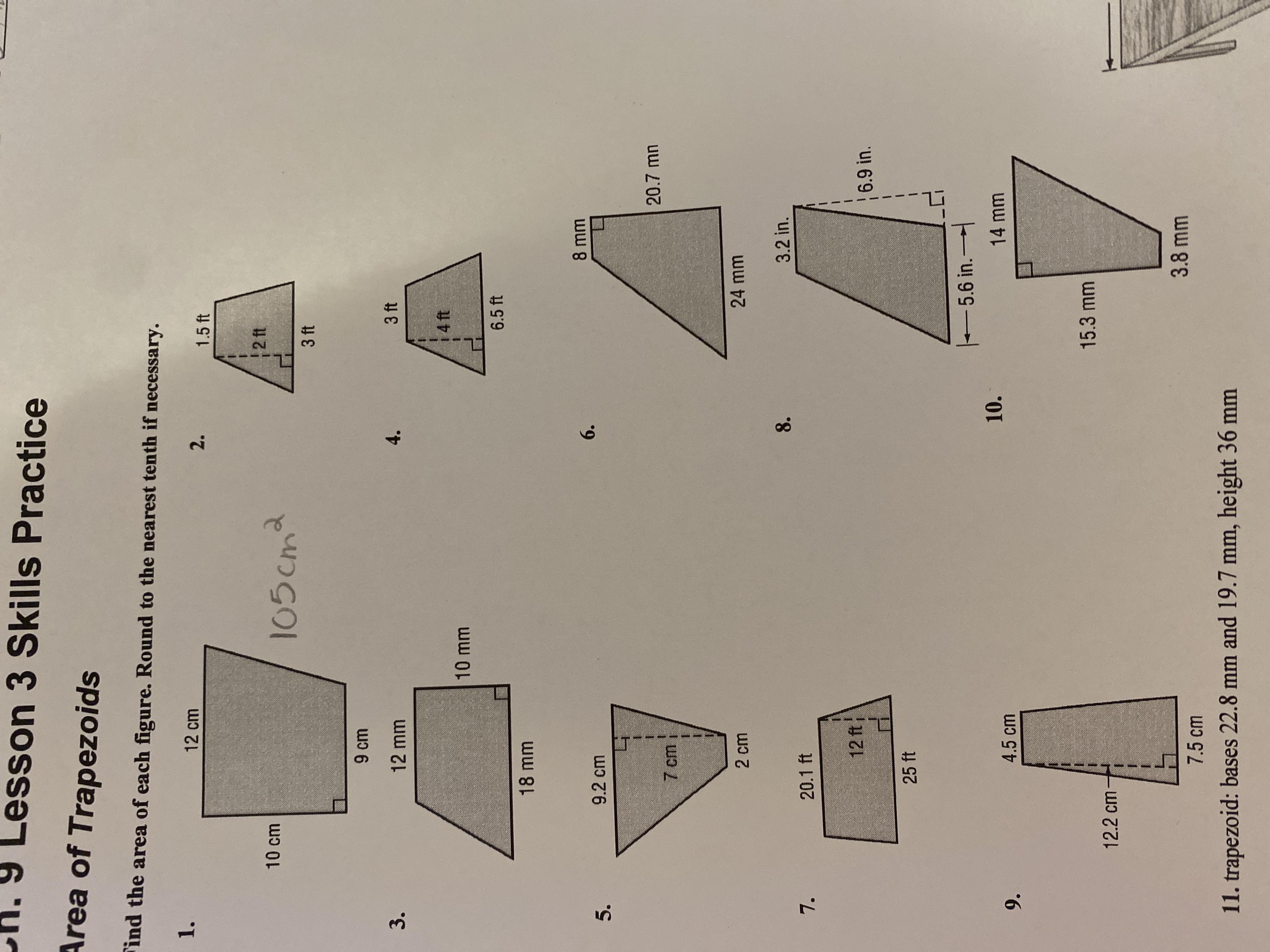
Answers
Answer:
15.5cm² for number one
Step-by-step explanation:
I will only do number one for you but here how you do it
1/2 (12+9) 10.
The 12 and 9 come from the top and bottem number and 10 come from the total height
Then we need to calucate
1/2(12+9)+10
1/2*21+10
1/2*31
31/2
15.5
So 15.5cm² is the answer for the first one now I think you can do the rest!
The Area of Trapezoids are:
1. 105 cm²
2. 6.75 ft²
3. 150 mm²
4. 19 ft²
5. 19.6 cm²
6. 331.2 mm²
7. 270.6 ft²
8. 30.36 in²
9. 73.2 cm²
10. 136.17 mm²
The formula of Area of Trapezoids is:
= 1/2 x (Sum of bases) x height
1. Area of Trapezoids is:
= 1/2 x (12 + 9) x 10
= 1/2 x 21 x 10
= 105 cm²
2. Area of Trapezoids is:
= 1/2 x (1.5+ 3) x 3
= 1/2 x 4.5 x 3
= 6.75 ft²
3. Area of Trapezoids is:
= 1/2 x (12 + 18) x 10
= 1/2 x 30 x 10
= 150 mm²
4. Area of Trapezoids is:
= 1/2 x (3 + 6.5) x 4
= 1/2 x 9.5 x 4
= 19 ft²
5. Area of Trapezoids is:
= 1/2 x (9.2+ 2) x 7
= 1/2 x 11.2 x 7
= 19.6 cm²
6. Area of Trapezoids is:
= 1/2 x (8 + 24) x 20.7
= 1/2 x 32 x 20.7
= 331.2 mm²
7. Area of Trapezoids is:
= 1/2 x (20.1 + 25) x 12
= 1/2 x 45.1
= 270.6 ft²
8. Area of Trapezoids is:
= 1/2 x (3.2 + 5.6) x 6.9
= 1/2 x 8.8 x 6.9
= 30.36 in²
9. Area of Trapezoids is:
= 1/2 x (4.5 + 7.5) x 12.2
= 1/2 x 12 x 12.2
= 73.2 cm²
10. Area of Trapezoids is:
= 1/2 x (14 + 3.8) x 15.3
= 1/2 x 17.8 x 10
= 136.17 mm²
Learn more about Area of Trapezoids here:
https://brainly.com/question/15640807
#SPJ6
combine terms/simolify

Answers
Answer:
\(\dfrac{2m -1}{5}\)
Step-by-step explanation:
Since we have common denominators inside the parentheses, we can combine the denominators. Then, we get the following expression:
\(2\huge\text{(}\dfrac{1}{5} m - \dfrac{2}{5} \huge\text{)} + \dfrac{3}{5}\)
\(2\huge\text{(}\dfrac{m - 2}{5} \huge\text{)} + \dfrac{3}{5}\)
Now, we can multiply the expression inside the parentheses by 2.
\(\huge\text{(}\dfrac{2m - 4}{5} \huge\text{)} + \dfrac{3}{5}\)
Since the expression inside the parentheses cannot be simplified further, we can open the parentheses and simplify the expression.
\(\dfrac{2m - 4}{5} + \dfrac{3}{5}\)
We can combine the denominators as the denominators are the same.
\(\dfrac{2m - 4 + 3}{5}\)
Finally, we can simplify -4 + 3.
\(\dfrac{2m -1}{5}\)
Therefore, the simplified expression is (2m - 1)/5.
Learn more about combining like terms: https://brainly.com/question/13080103
a force of 12N acts for 5 s on a mass of 2 kg. What is the change in momentum of a mass of 10kg under the same condition
Answers
Answer:
The change in momentum is: 60 N.s
Step-by-step explanation:
By Newton's second law:
F = ∆p / ∆t
Given that
∆t = 5sF = 12NUsing the formula to determine the change in momentum
F = ∆p / ∆t
∆p = F × ∆t
= 12 × 5
= 60 N.s
Therefore, the change in momentum is: 60 N.s
Multiply.
2x^4 (3x³ − x² + 4x)

Answers
Answer: A
Step-by-step explanation:
When multiplying: Numbers multiply with numbers and for the x's, add the exponents
If there is no exponent, you can assume an imaginary 1 is the exponent
2x⁴ (3x³ − x² + 4x)
= 6x⁷ -2x⁶ + 8x⁵
Answer:
A. \(6x^{7} - 2x^{6} + 8x^{5}\)
Step-by-StepLabel the parts of the expression:
Outside the parentheses = \(2x^{4}\)
Inside parentheses = \(3x^{3} -x^{2} + 4x\)
You must distribute what is outside the parentheses with all the values inside the parentheses. Distribution means that you multiply what is outside the parentheses with each value inside the parentheses
\(2x^{4}\) × \(3x^{3}\)
\(2x^{4}\) × \(-x^{2}\)
\(2x^{4}\) × \(4x\)
First, multiply the whole numbers of each value before the variables
2 x 3 = 6
2 x -1 = -2
2 x 4 = 8
Now you have:
6\(x^{4}x^{3}\)
-2\(x^{4}x^{2}\)
8\(x^{4} x\)
When you multiply exponents together, you multiply the bases as normal and add the exponents together
\(6x^{4+3}\) = \(6x^{7}\)
\(-2x^{4+2}\) = \(-2x^{6}\)
\(8x^{4+1}\) = \(8x^{5}\)
Put the numbers given above into an expression:
\(6x^{7} -2x^{6} +8x^{5}\)
Key Wordsdistribution
variable
like exponents
Given F(x,y)=(1 + xy)e^xyi + x^2e^xyj
(a) Show that F is conservative.
(b) Find a function f such that F = delf
(c) Use part (b) to evaluate integral F * dr where C is the curve with equation r(t) = costi + 2sintj
0 <= t <= 2 [Hint: Fundamental Theorem of Line Integrals].
Answers
(a) To show that F is conservative, we need to check if it satisfies the condition of being the gradient of a scalar function.
We can do this by taking the partial derivatives of the components of F with respect to x and y and checking if they are equal:
∂F/∂y = (1 + x^2y)e^xyi + (x^3y + 2xy)e^xyj
∂F/∂x = (1 + xy)e^xyi + (2xy + x^2)e^xyj
Since the mixed partial derivatives are equal (∂^2F/∂x∂y = ∂^2F/∂y∂x = (1+3xy)e^xy), F is conservative.
(b) To find f, we need to integrate the component functions of F with respect to the corresponding variables:
f(x,y) = ∫[(1 + xy)e^xy]dx = (x + 1)e^xy + g(y)
f(x,y) = ∫[x^2e^xy]dy = xe^xy + h(x)
where g(y) and h(x) are integration constants.
Taking the partial derivative of f with respect to x and y, we get:
∂f/∂x = (1 + xy)e^xy + yg'(y)
∂f/∂y = (1 + xy)e^xy + xg'(y) + xe^xyh'(x)
Comparing these with the components of F, we get:
β1 = 1 + xy, β2 = y, β3 = 0
β1 = 1 + xy, β2 = x^2, β3 = 0
Solving for g'(y) and h'(x), we get:
g'(y) = y
h'(x) = x
Integrating with respect to y and x, we get:
g(y) = 1/2 y^2 + C1
h(x) = 1/2 x^2 + C2
where C1 and C2 are integration constants.
Thus, the function f is:
f(x,y) = (x + 1)e^xy + 1/2 y^2 + C1 + 1/2 x^2 + C2
(c) Using the Fundamental Theorem of Line Integrals, we have:
∫CF.dr = ∫C(∇f).dr = f(r(2)) - f(r(0))
where r(0) and r(2) are the initial and final points of the curve C.
We have:
r(0) = cos(0)i + 2sin(0)j = i
r(2) = cos(2π)i + 2sin(2π)j = i
Substituting into the expression for f, we get:
f(r(0)) = (1 + 0)e^0i + 1/2(0)^2 + C1 + 1/2(1)^2 + C2 = C1 + C2 + 1/2
f(r(2)) = (1 + 0)e^0i + 1/2(0)^2 + C1 + 1/2(1)^2 + C2 = C1 + C2 + 1/2
Thus, the value of the line integral is:
∫CF.dr = f(r(2)) - f(r(0)) = (C1 + C2 + 1/2) - (C1 + C2 + 1/2) =
To know more about line integrals refer here:
https://brainly.com/question/30460707#
#SPJ11
The lengths of the sides of a triangle are 4,5 and 6 if the length of the longest side of a similar triangle is 15,what is the length of the shortest side of the triangle
Answers
Answer:
The length of the shortest side of the triangle is 10.
Step-by-step explanation:
Given that the lengths of the sides of a triangle are 4, 5 and 6, if the length of the longest side of a similar triangle is 15, to determine what is the length of the shortest side of the triangle, the following calculation must be performed :
6 = 15
4 = X
4 x 15/6 = X
10 = X
Therefore, the length of the shortest side of the triangle is 10.
in three plays of a football game, there is a gain of 4 yards, a loss of 9 yards, and a gain of 15 yards. What number can you use to represent a 9 yard loss?
Answers
We can use minus(-) sign i.e. -9 to represent loss of 9 yards.
Write the difference between gain and loss.The word “gain” implies “acquiring something”.
Gain means to acquire something one desires especially because of one’s efforts.
Gain means to get something additional, for example, to gain more speed, to gain more weight.
We can denote gain by using plus(+) sign before the given number.
“Loss” generally means “to lose something one already has.”
Loss means the deprivation from keeping something, for example, bearing the loss of a theft.
It refers to something which is lost, for example, the theft of jewelry was a great loss.
We can denote loss by using minus(-) sign before the number.
In the given question it is said that there is gain of 4 yards, loss of 9 yards and gain of 15 yards.
It is asked that how would we represent 9 yards loss.
We know that we use minus(-) sign to represent loss.
So we can represent loss of 9 yards by writing it as -9.
To learn more about gain and loss,
https://brainly.com/question/18281564
#SPJ9
, evaluate and simplify.

Answers
The difference quotient of the function f(x) = 4x² - 5x is 8x + 4h - 5.
What is the difference quotient of the given function?The formula for difference quotient is expressed as:
\(\frac{f(x+h)-f(x)}{h}\)
Given the function in the question:
f(x) = 4x² - 5x
To solve for the difference quotient, we evaluate the function at x = x+h:
First;
f(x + h) = 4(x + h)² - 5(x + h)
Simplifying, we gt:
f(x + h) = 4x² + 8hx + 4h² - 5x - 5h
f(x + h) = 4h² + 8hx + 4x² - 5h - 5x
Next, plug in the components into the difference quotient formula:
\(\frac{f(x+h)-f(x)}{h}\\\\\frac{(4h^2 + 8hx + 4x^2 - 5h - 5x - (4x^2 - 5x)}{h}\\\\Simplify\\\\\frac{(4h^2 + 8hx + 4x^2 - 5h - 5x - 4x^2 + 5x)}{h}\\\\\frac{(4h^2 + 8hx - 5h)}{h}\\\\\frac{h(4h + 8x - 5)}{h}\\\\8x + 4h -5\)
Therefore, the difference quotient is 8x + 4h - 5.
Learn more about difference quotient here: https://brainly.com/question/6200731
#SPJ1
find a value of c so that p(z ≥ c) = 0.55.
Answers
To find a value of c such that P(z ≥ c) = 0.55, we need to use a standard normal distribution table or calculator.From the standard normal distribution table, we find that the z-score corresponding to a right-tailed area of 0.55 is approximately 0.126.
Therefore, we have:
P(z ≥ c) = 0.55
P(z ≤ c) = 1 - P(z ≥ c) = 1 - 0.55 = 0.45
Using the standard normal distribution table, we find that the z-score corresponding to a left-tailed area of 0.45 is approximately -0.126.
So, c = -0.126.
Therefore, the value of c that satisfies P(z ≥ c) = 0.55 is approximately -0.126.
To learn more about distribution : brainly.com/question/29664127
#SPJ11
Mhanifa please help this is late and I don’t get it

Answers
Answer:
Sin k jajs
Step-by-step explanation:
What is the value of a in the equation 3a+b = 54, when b = 9?
O 15
O 18
18 k
O 21
O 27
Answers
Answer:
15
Step-by-step explanation:
Find the mean, median, and mode of the following set of data if a constant value 3 is added to every value in the data set: 2 10 9 8 8 8
Answers
Given data set have, Mean = 10.5, Median = 11, Mode = 11.
To find the mean, median, and mode of the given set of data after adding a constant value of 3 to each element, we need to follow these steps:
Step 1: Add 3 to each value in the data set:
2 + 3 = 5
10 + 3 = 13
9 + 3 = 12
8 + 3 = 11
8 + 3 = 11
8 + 3 = 11
The updated data set becomes: 5, 13, 12, 11, 11, 11
Step 2: Calculate the mean:
Mean = (sum of all values) / (number of values)
Mean = (5 + 13 + 12 + 11 + 11 + 11) / 6
Mean = 63 / 6
Mean = 10.5
The mean of the updated data set is 10.5.
Step 3: Calculate the median:
The median is the middle value in a sorted list of numbers.
First, let's sort the updated data set in ascending order: 5, 11, 11, 11, 12, 13
The median is the middle value, which in this case is the average of the two middle values:
Median = (11 + 11) / 2
Median = 22 / 2
Median = 11
The median of the updated data set is 11.
Step 4: Calculate the mode:
The mode is the value that appears most frequently in the data set.
In the updated data set: 5, 11, 11, 11, 12, 13, the mode is 11 since it appears three times, which is more than any other value.
Therefore, the mode of the updated data set is 11.
To summarize:
Mean = 10.5
Median = 11
Mode = 11
To know more about Median , refer here:
https://brainly.com/question/300591#
#SPJ11
AC is a diameter of OE, the area of
the
circle is 2897 units², and AB = 16 units.
Find BC and mBC.
B
A
C
E

Answers
Given that AC is a diameter of the circle, we can conclude that triangle ABC is a right triangle, with AC being the hypotenuse. The area of the circle is not directly related to finding the lengths of BC or AB, so we will focus on the given information: AB = 16 units.
Using the Pythagorean theorem, we can find BC. The Pythagorean theorem states that in a right triangle, the square of the length of the hypotenuse (AC) is equal to the sum of the squares of the other two sides (AB and BC):
AC² = AB² + BC²
Substituting the given values, we have:
(AC)² = (AB)² + (BC)²
(AC)² = 16² + (BC)²
(AC)² = 256 + (BC)²
Now, we need to find the length of AC. Since AC is a diameter of the circle, the length of AC is equal to twice the radius of the circle.
AC = 2 * radius
To find the radius, we can use the formula for the area of a circle:
Area = π * radius²
Given that the area of the circle is 2897 units², we can solve for the radius:
2897 = π * radius²
radius² = 2897 / π
radius = √(2897 / π)
Now we have the length of AC, which is equal to twice the radius. We can substitute this value into the equation:
(2 * radius)² = 256 + (BC)²
4 * radius² = 256 + (BC)²
Substituting the value of radius, we have:
4 * (√(2897 / π))² = 256 + (BC)²
4 * (2897 / π) = 256 + (BC)²
Simplifying the equation gives:
(4 * 2897) / π = 256 + (BC)²
BC² = (4 * 2897) / π - 256
Now we can solve for BC by taking the square root of both sides:
BC = √((4 * 2897) / π - 256)
To find the measure of angle BC (mBC), we know that triangle ABC is a right triangle, so angle B will be 90 degrees.
In summary:
BC = √((4 * 2897) / π - 256)
mBC = 90 degrees
for similar questions on area of the circle.
https://brainly.com/question/14068861
#SPJ8
4p+6-3 combine like terms to get equivalent expressions
Answers
Answer:
4p+3
Step-by-step explanation:
4p+6+-3
[4p]+[6+-3]
4p+3
If A and B are any two events defined on a sample space S of an experiment, then p(A ∩ B) = p(A).p(B)
True or False
Answers
The statement is True only for independent events and False otherwise. The statement "p (A ∩ B) = p(A). p(B)" is not always true for any two events A and B defined on a sample space S of an experiment.
This equation only holds true if A and B are independent events, meaning that the occurrence of one event does not affect the probability of the other event happening. In other words, p(A|B) = p(A) and p(B|A) = p(B).
If A and B are dependent events, meaning that the occurrence of one event affects the probability of the other event happening, then the equation does not hold true. In this case, the probability of A and B occurring together (p(A ∩ B)) would be less than the product of the probabilities of A and B occurring separately (p(A).p(B)).
Therefore, the statement is not always true and depends on whether A and B are independent or dependent events.
Learn more about experiment here:
brainly.com/question/28198971
#SPJ11
Let the long-run profit function for a representative firm is given by π i
=p 2
−2p−399, where p is the price of computer. The inverse market demand for computer is given by p=39−0.009q, where q is unit of computers. Suppose technology for producing computers is identical for all firms and all firms face identical input prices. (a) Find the firm's output supply function. (b) Find the market-equilibrium price and the equilibrium number of firms. (c) Find the number of computers sold by each firm in the long run.
Answers
(a) The firm's output supply function is given by q = (p + 199) / 2.
(b) The market-equilibrium price is $32.56, and the equilibrium number of firms is 10.
(c) Each firm sells 70 computers in the long run.
To find the firm's output supply function, we need to maximize the firm's profit function, which is given by π = p^2 - 2p - 399. In the long run, firms will produce where marginal cost equals marginal revenue. Marginal revenue can be obtained by differentiating the inverse market demand function with respect to q, and marginal cost is equal to the derivative of the profit function with respect to q. Equating the two, we get:(39 - 0.009q) = (2q - 2) / q
Simplifying the equation, we find:
q = (p + 199) / 2
This represents the firm's output supply function.
To find the market-equilibrium price and the equilibrium number of firms, we need to find the intersection point of the market demand and supply. Substituting the output supply function into the inverse market demand function, we have:p = 39 - 0.009((p + 199) / 2)
Simplifying and solving for p, we get:
p ≈ $32.56
Substituting this price back into the output supply function, we find:
q = (32.56 + 199) / 2 ≈ 115.78
Given that each firm produces 70 computers in the long run, we can calculate the equilibrium number of firms:
Number of firms = q / 70 ≈ 10
Since each firm sells 70 computers in the long run, and there are 10 firms, the total number of computers sold by each firm is:70 * 10 = 700
Learn more about Equilibrium
brainly.com/question/30694482
#SPJ11
how to determine density of a liquid with cubes, a meterstick and stopwatch
Answers
The formula to determine the density of a liquid with cubes, a meterstick and stopwatch is density of the liquid = mass / volume = 2.7 g / (volume of liquid displaced by the cube)
Density is a measure of how much mass is contained in a given volume of a material. In order to determine the density of a liquid, you will need three things: cubes, a meterstick, and a stopwatch.
First, gather your materials and select a cube of known dimensions. Place the cube on the surface of the liquid and start the stopwatch. Observe how long it takes for the cube to sink to the bottom of the container. Let's call this time t.
Next, use the meterstick to measure the height of the liquid in the container
With these two pieces of information, you can calculate the density of the liquid using the formula:
=> density = mass / volume
The mass of the cube can be calculated as:
=> mass = volume * density of the cube
where the volume of the cube is given by
=> volume = s³, where s is the length of one side.
Since we know the length of one side (s = 1 cm), the volume of the cube is 1 cm³.
The density of the cube can be assumed to be a constant value (for example, if the cube is made of aluminum, the density is approximately 2.7 g/cm³).
So,
=> mass = volume * density of the cube = 1 cm³ * 2.7 g/cm³ = 2.7 g.
The volume of the liquid displaced by the cube can be calculated as:
volume = mass / density of the liquid = mass / (h/t²)
where h/t² is the acceleration due to gravity.
Finally,
density of the liquid = mass / volume = 2.7 g / (volume of liquid displaced by the cube)
Complete Question:
Determine the density of an unknown liquid with only a meterstick, stopwatch, and cubes that sink.
To know more about density here.
https://brainly.com/question/17594847
#SPJ4
what is the radius of a circle inscribed in a 9-12-15 triangle?
Answers
The radius of the circle inscribed in a 9-12-15 triangle is 3 units
The radius of a circle inscribed in a 9-12-15 triangle can be found using the formula for the inradius (r) of a triangle:
r = A/s
where A is the area of the triangle, and s is the semi-perimeter of the triangle.
Step 1: Find the semi-perimeter (s)
s = (a + b + c) / 2
s = (9 + 12 + 15) / 2
s = 36 / 2
s = 18
Step 2: Find the area (A) of the triangle using Heron's formula:
A = √(s(s-a)(s-b)(s-c))
A = √(18(18-9)(18-12)(18-15))
A = √(18(9)(6)(3))
A = √(2916)
A = 54
Step 3: Find the inradius (r) using the formula r = A/s:
r = 54 / 18
r = 3
Therefore, the radius of the circle inscribed in a 9-12-15 triangle is 3.
TIP: A circle inscribed in a triangle is a circle that touches all three sides of the triangle exactly once, and it is positioned entirely within the triangle.
#SPJ11
i need help please only help if you know the answer

Answers
Answer:
D
Step-by-step explanation:
The diameter of a circular pizza is 24 in. How much pizza is eaten (in square inches) if half of it is consumed? (Pie and л... hmmmm...interesting...)
Answers
Using the formula of area of a circle, about 226.08in² has been eaten
How much pizza is eaten?The diameter of the pizza is given as 24 inches. To calculate the area of the entire pizza, we need to use the formula for the area of a circle:
Area = π * r²
where π is approximately 3.14 and r is the radius of the circle.
Given that the diameter is 24 inches, the radius (r) would be half of the diameter, which is 12 inches.
Let's calculate the area of the entire pizza first:
Area = 3.14 * 12²
Area = 3.14 * 144
Area ≈ 452.16 square inches
Now, if half of the pizza is consumed, we need to calculate the area of half of the pizza. To do that, we divide the area of the entire pizza by 2:
Area of half of the pizza = 452.16 / 2
Area of half of the pizza ≈ 226.08 square inches
Therefore, if half of the pizza is consumed, approximately 226.08 square inches of pizza would be eaten.
Learn more on area of a circle here;
https://brainly.com/question/15673093
#SPJ1
The scale of a map says that 6 cm represents 15 km,
What is the actual number of kilometers that is represented by 16 cm on the map