Write the equation of the line that is perpendicular to the graph of 2x + y = 5, and whose y-intercept is 4.
Answers
the equation of the line that is perpendicular to 2x + y = 5 and has a y-intercept of 4 is y = 1/2 x + 4.
What is equation straight line?
Y = mx + c is the general equation for a straight line, where m denotes the line's slope and c the y-intercept. It is the version of the equation for a straight line that is used most frequently in geometry. There are numerous ways to express the equation of a straight line, including point-slope form, slope-intercept form, general form, standard form, etc. A straight line is a geometric object with two dimensions and infinite lengths at both ends. The formulas for the equation of a straight line that are most frequently employed are y = mx + c and axe + by = c. Other versions include point-slope, slope-intercept, standard, general, and others.
First, we can rewrite 2x + y = 5 in slope-intercept form (y = mx + b) by solving for y:
y = -2x + 5
So the slope of the given line is -2.
The negative reciprocal of -2 is 1/2, so the slope of the line perpendicular to the given line is 1/2.
Next, we know that the y-intercept of the perpendicular line is 4, so we can use the point-slope form of a line to write the equation:
y - y1 = m(x - x1), where m is the slope and (x1, y1) is a point on the line.
Substituting m = 1/2 and (x1, y1) = (0, 4), we get:
y - 4 = 1/2(x - 0)
Simplifying, we get:
y = 1/2 x + 4
So the equation of the line that is perpendicular to 2x + y = 5 and has a y-intercept of 4 is y = 1/2 x + 4.
Learn more about straight line, by the following link
https://brainly.com/question/16949303
#SPJ1
Related Questions
has one real eigenvalue. find this eigenvalue, its multiplicity, and the dimension of the corresponding eigenspace.
Answers
one real eigenvalue. find this eigenvalue, its multiplicity, and the dimension of the corresponding eigenspace.
What is eigenvalue?
In linear algebra, an eigenvector or characteristic vector of a linear transformation is a nonzero vector that, when the linear transformation is applied to it, changes at most by a scalar factor. The factor by which the eigenvector is scaled is known as the associated eigenvalue, frequently denoted by lambda.
a) -4
b) 1
c) 1
Step-by-step explanation:
a) The matrix A is given by:
\(A=\left[\begin{array}{ccc}-3 & 0 & 1 \\2 & -4 & 2 \\-3 & -2 & 1\end{array}\right]\\\)
where lambda are the eigenvalues and I is the identity matrix. By replacing you obtain:
\(A-\lambda I=\left[\begin{array}{ccc}-3-\lambda & 0 & 1 \\2 & -4-\lambda & 2 \\-3 & -2 & 1-\lambda\end{array}\right]\)
and by taking the determinant:\(\begin{aligned}& {[(-3-\lambda)(-4-\lambda)(1-\lambda)+(0)(2)(-3)+(2)(-2)(1)]-[(1)(-4-\lambda)(-3)+(0)(2)(1-} \\& \lambda)+(2)(-2)(-3-\lambda)]=0 \\& -\lambda^3-6 \lambda^2-12 \lambda-16=0\end{aligned}\)
and the roots of this polynomial is:
\(\begin{aligned}& \lambda_1=-4 \\& \lambda_2=-1+i \sqrt{3} \\& \lambda_3=-1-i \sqrt{3}\end{aligned}\)
hence, the real eigenvalue of the matrix A is -4.
b) The multiplicity of the eigenvalue is 1.
c) The dimension of the eigenspace is 1 (because the multiplicity determines the dimension of the eigenspace)
To learn more about eigenvalue visit
https://brainly.com/question/29579848
#SPJ4
Complete Quetion
The matrix A= (−3 0 1, 2 −4 2, −3 −2 1) has one real eigenvalue. Find this eigenvalue, its multiplicity, and the dimension of the corresponding eigenspace. The eigen value = has multiplicity = and the dimension of the corresponding eigenspace is:_______.
Round 71.916476787 to 1 decimal place.
Answers
Answer:
71.9
Step-by-step explanation:
Whenever you want to round a number to a particular digit, look only at the digit immediately to its right. For example, if you want to round to the nearest tenth, look to the right of the tenths place: This would be the hundredths place digit. Then, if it is 5 or higher, you get to add one to the tenths digit.
After rounding 71.916476787 to 1 decimal place we get 71.9.
What is rounding of numbers ?We round numbers to get an approximate value of the given number in more compact form and which is easy to work with.
According to the given question we have to round 71.916476787 to 1 decimal place.
So, to round 71.916476787 to 1 decimal place we'll look at the digit of 2 decimal place here in this number it is 1 hence it is less than 5 so we can make all the digits after 1 decimal places zero and rewrite this number as
71.900000000 and we know zeroes are meaning less to the right of the decimal so this can be written as 71.9.
learn more about rounding of numbers :
https://brainly.com/question/28562556
#SPJ2
use appendix table 5 and linear interpolation (if necessary) to approximate the critical value 0.15,10.value t0.15,10. (use decimal notation. give your answer to four decimal places.)
Answers
The approximate critical value t0.15,10 using linear interpolation is 1.8162.
Using Appendix Table 5, we need to approximate the critical value t0.15,10. For this, we'll use linear interpolation.
First, locate the values in the table nearest to the desired critical value. In this case, we have t0.15,12 and t0.15,9. According to the table, these values are 1.7823 and 1.8331, respectively.
Now, we'll apply linear interpolation. Here's the formula:
t0.15,10 = t0.15,9 + (10 - 9) * (t0.15,12 - t0.15,9) / (12 - 9)
t0.15,10 = 1.8331 + (1) * (1.7823 - 1.8331) / (3)
t0.15,10 = 1.8331 + (-0.0508) / 3
t0.15,10 = 1.8331 - 0.0169
t0.15,10 ≈ 1.8162
So, the approximate critical value t0.15,10 using linear interpolation is 1.8162.
Visit here to learn more about linear interpolation :
brainly.com/question/30766137
#SPJ11
Read the excerpt from "The Tell-Tale Heart."
Which statement best explains how the reader can
determine that the narrator is unreliable?
But you should have seen me. You should have seen
how wisely I proceeded—with what caution—with what
foresight—with what dissimulation I went to work! I was
never kinder to the old man than during the whole week
before I killed him. And every night, about midnight, I
turned the latch of his door and opened it-oh so
gently! And then, when I had made an opening
sufficient for my head, I put in a dark lantern, all closed,
closed, that no light shone out, and then I thrust in my
head. Oh, you would have laughed to see how
cunningly I thrust it in!
O The narrator is very kind to the old man during the
whole week before the murder.
O The narrator checks on the old man every night at
midnight to ensure his well-being.
O The narrator closes the lantern tightly so the old
man is not awakened by the bright light.
O The narrator believes that his audience will approve
of and even laugh at his plot to murder the old man.
Answers
Answer:
The narrator checks the old man at every night at midnight
Step-by-step explanation:
An amateur drama group hire a theatre for their production. They expect to sell all 850 tickets, some at $12 and the rest at $8. The group require the ticket sales to cover their $3760 production costs and to make a profit of $4000. If they are to exactly achieve this target and their expectations regarding ticket sales are correct how many of the 850 tickets should they charge $12 for and how many should they charge $8 for?
Answers
Answer:
610 tickets for $8, and 240 tickets for $12.
Step-by-step explanation:
x + y = 850
8x + 12y = 7760
x = 850 - y
8(850-y) + 12y = 7760
6800 - 8y + 12y = 7760
4y = 960
y= 240
x + 240 = 850
x= 610
Answer:
240 = no. of $12 tickets
610 = no. of $8 tickets
Step-by-step explanation:
Let x = no. of $12 tickets
y = no. of $8 tickets
12x = income from selling x $12 tickets
8y = income from selling y $8 tickets
If they are to make a profit of 4000, then they need to have a total income from sales of $7760
So, x + y = 850 and 12x + 8y = 7760
y = 850 - x 12x + 8(850 - x) = 7760
12x + 6800 - 8x = 7760
4x + 6800 = 7760
4x = 960
x = 240 = no. of $12 tickets
y = 850 - 240
= 610 = no. of $8 tickets
a.Explain how ships enter and leave a port and a harbour
b.what is a transit harbour, ,point of convergence, gate way port
c. discuss the 4 factors that affects the design of modern ports
Answers
Ships enter and leave a port or harbor through a process known as "ship navigation." When a ship approaches a port or harbor, it follows a designated shipping channel or fairway. This channel is usually marked by buoys or beacons to guide the ship safely.
Environmental considerations: Modern port design takes into account environmental factors, such as coastal erosion, water quality, and marine habitat protection. Ports may need to incorporate measures to minimize the impact on the environment, such as the use of environmentally friendly construction materials, waste management systems, or the implementation of measures to reduce air and water pollution.
In summary, ships enter and leave a port or harbor through ship navigation, which involves following a designated shipping channel. A transit harbor is a stopover location for ships, a point of convergence is where shipping routes intersect, and a gateway port is a major hub for international trade. The design of modern ports is influenced by factors such as geography, traffic volume, accessibility, and environmental considerations.
To know more about marked visit:
https://brainly.com/question/30078912
#SPJ11
Help me fast I’ll mark brainliest plzzz

Answers
Answer:
1 2 3 4 5 6 7 8 9 10 11
Step-by-step explanation:
Answer:
Since I don't have the numbers to plot, I'll tell you where to begin
Step-by-step explanation:
When plotting temperatures, it's important to remember positives and negatives
It's always a good idea to start by marking the halfway point as zero
Then, if the numbers are in the tens, make each increment an increasing value of ten/-ten in each direction.
If they're low, (in the ones digits) then just mark the numbers on the increments in the positive/negative directions
Hope this helps!
Find the volume of the solid lying under the circular paraboloid z = x2 + y2 and above the rectangle R = (-4,4] x [-6,6). 1. 2496 2. 1664 3. 1248 4. 960 5. 640
Answers
According to the question we have the correct answer is option 2, with a volume of 1664 cubic units.
The volume of the solid lying under the circular paraboloid z = x^2 + y^2 and above the rectangle R = (-4, 4] x [-6, 6] can be found using a double integral. First, set up the integral with respect to x and y over the given rectangular region:
Volume = ∬(x^2 + y^2) dA
To evaluate this integral, we will use the limits of integration for x from -4 to 4, and for y from -6 to 6:
Volume = ∫(from -4 to 4) ∫(from -6 to 6) (x^2 + y^2) dy dx
Now, integrate with respect to y:
Volume = ∫(from -4 to 4) [(y^3)/3 + y*(x^2)](from -6 to 6) dx
Evaluate the integral at the limits of integration for y:
Volume = ∫(from -4 to 4) [72 + 12x^2] dx
Next, integrate with respect to x:
Volume = [(4x^3)/3 + 4x*(72)](from -4 to 4)
Evaluate the integral at the limits of integration for x:
Volume = 1664
Therefore, the correct answer is option 2, with a volume of 1664 cubic units.
To know more about Volume visit :
https://brainly.com/question/28058531
#SPJ11
Minimizing Loss Numerical Example (1) puntos posibles (calificables Consider minimizing the above objective fuction for the following numerical example: A =0.5,y = 1,2 = Lo] Note that this is classification probl em where points lie on two dimensional space_ Hence would be two dimensiona vector. Let & 01, 82 where 81, 82 are the first and second components of € respectively: Solve for 81 , 82. Hint: For the above example; show that Lossh (y (0 . 2)) <0 Enviar Ha realizado intento: Guardar Minimizing Loss Numerical Example (2) punto posible (calificable} Now; let 0 be tne solution as function of A. Fcr what value of Izl? _ the training example (2,y) will be misclassified by 8 (A)? Ilzll?
Answers
For the given numerical example in a classification problem, the logistic loss function is always less than or equal to zero, indicating that a solution that minimizes the objective function cannot be found, possibly due to non-linearly separable data.
Since this is a classification problem with binary labels, we can use the logistic loss function given by:
L(y, h(x)) = log(1 + exp(-y * h(x)))
where y is the true label (either 1 or -1), h(x) is the predicted value, and exp is the exponential function.
In this case, λ = 0.5, y = 1, x = [10], and θ^ = [θ1^,θ2^]. We want to minimize the objective function:
f(θ^) = λ/2 * ||θ^||^2 + L(y, θ^ · x)
Substituting in the values, we get:
f(θ^) = 0.25 * (θ1^2 + θ2^2) + log(1 + exp(-θ1^ * 10))
To solve for θ1^ and θ2^, we need to find the partial derivatives of f(θ^) with respect to θ1^ and θ2^ and set them equal to zero:
∂f(θ^)/∂θ1^ = 0.1 * exp(-θ1^ * 10) * (1 / (1 + exp(-θ1^ * 10))) + 0.5 * θ1^ = 0
∂f(θ^)/∂θ2^ = 0.5 * θ2^ = 0
The second equation gives θ2^ = 0. Setting the first equation to zero and simplifying, we get:
exp(-θ1^ * 10) = -5
Since the exponential function is always positive, there are no solutions to this equation. However, we can use the hint given in the problem to show that the loss function is always less than or equal to zero for this example:
L(y, θ^ · x) = log(1 + exp(-10 * θ1^))
= log(1 + exp(-10 * (θ1^ - log(5))))
Since exp(-10 * (θ1^ - log(5))) is always less than or equal to 1, log(1 + exp(-10 * (θ1^ - log(5)))) is always less than or equal to 0. Therefore, the loss function is always less than or equal to 0.
So, we cannot find a solution that minimizes the objective function for this example. This suggests that the data is Non -linearly separable.
To know more about non-linearly separable data:
https://brainly.com/question/30612985
#SPJ4
_____The given question is incomplete, the complete question is given below:
Consider minimizing the above objective fuction for the following numerical example:
λ=0.5,y=1,x=[10]
Note that this is a classification problem where points lie on a two dimensional space. Hence θ^ would be a two dimensional vector.
Let θ^=[θ1^,θ2^], where θ1^,θ2^ are the first and second components of θ^ respectively.
Solve for θ1^,θ2^.
Hint: For the above example, show that Lossh(y(θ^⋅x))≤0
List the factor pairs of the number 16
Answers
Answer:(1,16) and (-1,-16)
Step-by-step explanation:
For example, the pair factors of 16 are written as
Do only equations with variables on both sides have no solution? Or can the variable be just on one side? Justify your answer. Choose the correct answer below.
A. Every equation with variables on both sides has no solution. However, it is also possible for an equation with the variable on only one side to also have no solution.
B. If the variable only appears on one side of an equation, then the equation can always be solved for the variable. This means that if an equation has no solution, then the variable must appear on both sides.
C. Any equation can have one solution, infinitely many solutions, or no solutions. This does not depend on whether the variable appears on only one side or on both sides.
D. If the variable only appears on one side of an equation, then the equation can always be solved for the variable. By contrast, an equation with variables on both sides always has no solution or infinitely many solutions.
Answers
Answer:
No only variable on both sides have no solution
Step-by-step explanation:
Then you can get,
for example x=x
or,
y=y
Answer:
Option CStep-by-step explanation:
A. Every equation with variables on both sides has no solution. However, it is also possible for an equation with the variable on only one side to also have no solution.
False, the first pat incorrect. The equation can be simplified to have variable on one side and solved further.B. If the variable only appears on one side of an equation, then the equation can always be solved for the variable. This means that if an equation has no solution, then the variable must appear on both sides.
False, the second part is incorrect. If an equation has no solution, then variables disappear and it results in nonsense equation.C. Any equation can have one solution, infinitely many solutions, or no solutions. This does not depend on whether the variable appears on only one side or on both sides.
TrueD. If the variable only appears on one side of an equation, then the equation can always be solved for the variable. By contrast, an equation with variables on both sides always has no solution or infinitely many solutions.
False, the second part is incorrect. The variables can be taken to the same side of equation. If they cancel and leave a correct equation, then it results in infinitely many solutions. If they cancel and leave incorrect equation, then it results in no solution. If it simplifies with variable on one side, then there is one solution.Find the value of y

Answers
Answer:
y = 39
Step-by-step explanation:
3x + 45 = 7x - 7
52 = 4x
x = 13
3(13) + 45 = 84
63 + 84 + (y - 6) = 180
y-6 = 33
y = 39
Help me am confused

Answers
9514 1404 393
Answer:
{ (-441/23, 433/23) }
Step-by-step explanation:
The "cross-multiplication method" is usually shown as follows:
1. rewrite the equations in general form: ax +by +c = 0
2. write the coefficients in two row in the order b, c, a, b.
3. form three products, each being the number in the first row times the number to its right in the second row. That is, b1·c2, c1·a2, a1·b2
4. form three more products, each being the number in the second row times the number to its right in the first row. That is, b2·c1, c2·a1, a2·b1
5. form three differences, subtracting the products of step 4 from those of step 3. Call these differences d1, d2, d3. (For example, d1=b1c2-b2c1.)
6. The values of x and y satisfy the equations ...
x/d1 = y/d2 = 1/d3
which is to say, ...
x = d1/d3, and y = d2/d3
_____
For your equations, we can rewrite them as ...
11x +12y -15 = 012x +11y +23 = 0Then our rows of coefficients are ...
\(\begin{array}{cccc}12&-15&11&12\\11&23&12&11\end{array}\)
And our differences are ...
d1 = 12(23) -11(-15) = 441
d2 = -15(12) -23(11) = -433
d3 = 11(11) -12(12) = -23
The relations between x and y are ...
x/441 = y/-433 = 1/-23
so, x = -441/23 and y = 433/23
The solution set is one ordered pair: { (-441/23, 433/23) }.
_____
Additional comments
The final solution is identical to the formula arrived at using Cramer's Rule. Calling this the "cross-multiplication method" avoids any discussion of matrices and determinants.
PLEASE HELP! WILL MARK BRAINLIEST - What is 2(n+1)?
Answers
Answer:
I hope that this helps... (2n-1)
Step-by-step explanation:
1)If n is a natural number, (2n-1) is an odd number for n greater or equal to 2 .
2) Is n is a whole the number the same thing applies but the range of n just has its vertex at -1.(Odd integer)
3)If n is any integer, then the range is all integers from -Infinity to +Infinity.(Odd integer)
4)If n is any complex number, n can be represented in the form of e^i thetha (Euler’s form) but nothing can b e commented on whether it is odd or even.
5)If n is any real number the range of this data can be from -Infinity to +Infinity, nothing can be commented on whether the number is odd or even.
What scenario could be modeled by the graph below?
A. The number of pounds of apples, y, minus two times the number of pounds of oranges, x, is at most 5.
B. The number of pounds of apples, y, minus half the number of pounds of oranges, x, is at most 5.
C. The number of pounds of apples, y, plus two times the number of pounds of oranges, x, is at most 5.
D. The number of pounds of apples, y, plus half the number of pounds of oranges, x, is at most 5.

Answers
Answer:
I would believe that it is A.
Step-by-step explanation:
The fact that A has 5, and x is minus two times, 5/2= 2.5, and that is where the second arrowhead is pointing to on the x axis.
The number of pounds of apples, y, minus two times the number of pounds of oranges, x, is at most 5 which is correct option (A).
What is graph?A graph can be defined as a pictorial representation or a diagram that represents data or values.
What is a Linear Function?A linear function is defined as a function in the form of f(x) = mx + bc where 'm' and 'c' are real numbers.
It represents the line's slope-intercept form, which is written as y = mx + c.
This is because a linear function represents a line, i.e., its graph is a line. Here,
'm' is the slope of the line
'c' is the y-intercept of the line
'x' is the independent variable
'y' (or f(x)) is the dependent variable
According to given graph,
A has a value of 5, and since x is negative two times, 5/2=2.5, which is where the second arrowhead on the x axis is pointing.
So, the total number of the pounds of apples, y minus two times, and the pounds of oranges, x, equals at most five pounds.
Hence, the number of pounds of apples, y, minus two times the number of pounds of oranges, x, is at most 5.
Learn more about graph here:
brainly.com/question/16608196
#SPJ5
Quadrilateral ABCD is inscribed in circle O. If M

Answers
Solution
For this case we can use the following equation:
m < A+ m < C= 180 º= m < B + m < D
Then since we know that m < A= 88º we can do this
m < C= 180º- 88º = 92º
then the correct answer is:
92º
the lengths of songs on the radio are normally distributed with a mean length of 210 seconds. if 38.2% of all songs have lengths between 194 and 226 seconds, then the standard deviation of this distribution is
Answers
Answer:
Step-by-step explanation:
6 = 2(y +2)
What does y equal
Answers
Answer:
One
Step-by-step explanation:
6=2(y+2)
Distribute 2
6=2y+4
-4 -4
2=2y
______
2
y=1
Answer:
y = 1
Step-by-step explanation:
First, you need to use the distributive property to simplify:
6 = 2y + 4
Then, subtract 4 from both sides, so you get the numbers on one side and the variables on the other.
2 = 2y
Divide both sides by 2, and . . .
y = 1
Define Torsion, pure torsion and it's assumptions, torsion
equation and limitation of its formula?
Answers
Torsion refers to the twisting of a structural member due to the application of torque. Pure torsion occurs when a structural member is subjected to torsional loading only. It is analyzed using assumptions such as linear elasticity, circular cross-sections, and small deformations. The torsion equation relates the applied torque, the polar moment of inertia, and the twist angle of the member. However, this formula has limitations in cases of non-circular cross-sections, material non-linearity, and large deformations.
Torsion is the deformation that occurs in a structural member when torque is applied, causing it to twist. In pure torsion, the member experiences torsional loading without any other external forces or moments acting on it. This idealized scenario allows for simplified analysis and calculations. The assumptions made in pure torsion analysis include linear elasticity, which assumes the material behaves elastically, circular cross-sections, which simplifies the geometry, and small deformations, where the twist angle remains small enough for linear relationships to hold.
To analyze pure torsion, engineers use the torsion equation, also known as the Saint-Venant's torsion equation. This equation relates the applied torque (T), the polar moment of inertia (J), and the twist angle (θ) of the member. The torsion equation is given as T = G * J * (dθ/dr), where G is the shear modulus of elasticity, J is the polar moment of inertia of the cross-section, and (dθ/dr) represents the rate of twist along the length of the member.
However, the torsion equation has its limitations. It assumes circular cross-sections, which may not accurately represent the geometry of some structural members. Non-circular cross-sections require more complex calculations using numerical methods or specialized formulas. Additionally, the torsion equation assumes linear elasticity, disregarding material non-linearity, such as plastic deformation. It also assumes small deformations, neglecting cases where the twist angle becomes significant, requiring the consideration of non-linear relationships. Therefore, in practical applications involving non-circular cross-sections, material non-linearity, or large deformations, more advanced analysis techniques and formulas must be employed.
To learn more about torsion click here: brainly.com/question/30612977
#SPJ11
The mean SAT score in mathematics is 501. The standard deviation of these scores is 30. A special preparation course claims that the mean SAT score, u, of its graduates is greater than 501. An independent researcher tests this by taking a random sample of 60 students who completed the course; the mean SAT score in mathematics for the sample was 511. At the 0.01 level of significance, can we conclude that the population mean SAT score for graduates of the course is greater than 501? Assume that the population standard deviation of the scores of course graduates is also 30. Perform a one-tailed test. Then complete the parts below. Carry your intermediate computations to three or more decimal places, and round your responses as specified below. (If necessary, consult a list of formulas.) (a) State the null hypothesis H, and the alternative hypothesis H. μ o p H : X S х Х 5 (d) Find the critical value. (Round to three or more decimal places.) 0 (e) Can we support the preparation course's claim that the population mean SAT score of its graduates is greater than 501? Yes O No
Answers
A) the Null and Alternative hypothesis are:
H0: μ = 501
H1: μ > 501
B) Test Statistics is 2.59
C) The critical value is 2.306
D) we can reject the null hypothesis and conclude that there is sufficient evidence to support the preparation course's claim that the population mean SAT score of its graduates is greater than 501.
What is null and Alternative hypothesis?The null hypothesis is a statement that assumes no significant difference or relationship, while the alternative hypothesis suggests otherwise.
A) So, the Null and Alternative hypothesis are:
H0: μ = 501
H1: μ > 501
B) Test stattisic
t = (x - μ) / (s / √n)
= (511 - 501) / (30 / √60)
= 2.59
C) Critical Value
α = 0.01
df = n - 1 = 60 - 1 = 59
tα = 2.306
D) Since the test statistic (2.59) is greater than the critical value (2.306), we can reject the null hypothesis and conclude that there is sufficient evidence to support the preparation course's claim that the population mean SAT score of its graduates is greater than 501.
Learn more about hypotheses:
https://brainly.com/question/606806
#SPJ4
NEED HELP ASAP ALGEBRA 1
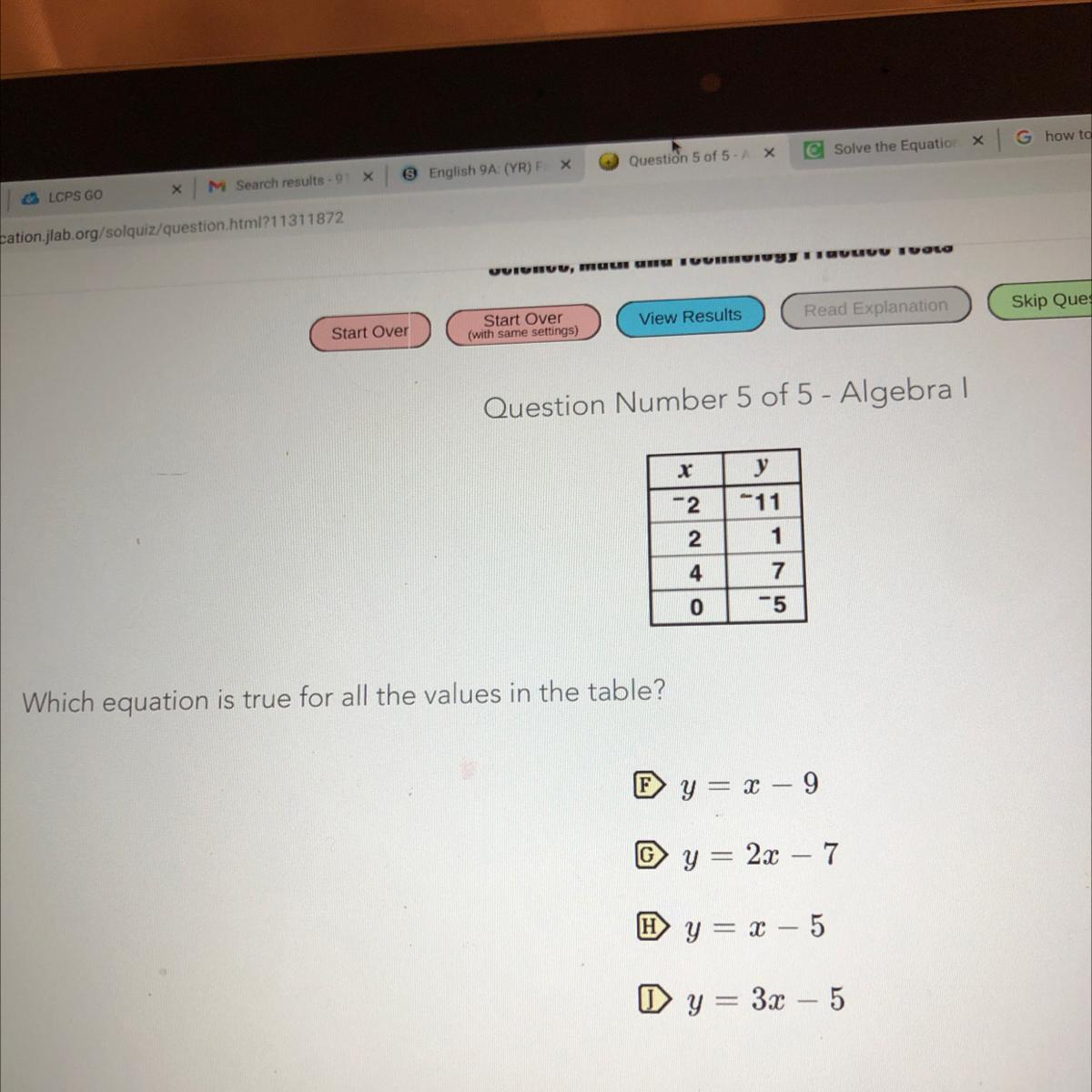
Answers
Answer:
The answer is the last one.
Answer: the answer is J
Step-by-step explanation:
what is 346924632968/33656
Answers
Answer:
Your answer is 10307957.956 :)
Step-by-step explanation:
346924632968/33656 = 10307957.956
have an amazing day!!
Please rate and mark brainliest!!
The correct answer: is 10307957.956:).
The price of a CD increased from $20 to $24. Find the percent of increase
Answers
Explanation:
4/24*100%
true ir false .
A central angle is equal to half the measure of its intercepted arc.
Answers
Answer:
Step-by-step explanation:
Answer
False but close.
The intercept arc and the central angle are equal.
Math work...HELPPPP!

Answers
1/8 unit- 3
1/8 of 24 = 3
A piece of land ABCD is in the shape of a trapezium
as shown in the diagram. AB = 40 m, BC = 39 m,
AD = 30 m, and <ABC = <BAD = 90°. Find
(a) the length of the side CD,
(b) angle BCD,
(c) the area of the land.

Answers
Answer:
a) CD = 41 m
b) 77.32°
c) 1380 square metres
Step-by-step explanation:
We can divide the trapezium as shown in the diagram below.
a) To find CD, we use Pythagoras Rule:
\(CD^2 = 9^2 + 40^2\)
\(CD^2 = 81 + 1600\\\\CD^2 = 1681\\\\=> CD = 41 m\)
b) To find <BCD, we use trigonometric function SOHCAHTOA:
sin(BCD) = opp / hyp
sin(BCD) = 40 / 41
sin(BCD) = 0.9756
=> <BCD = 77.32°
c) The area of a trapezium is given as:
A = 1/2 (a + b) * h
where h = height = 40 m
a = top length = 30 m
b = bottom length = 39 m
A = 1/2 * (30 + 39) * 40
A = 1/2 * 69 * 40
A = 1380 square metres

Why should the data be partitioned into training and validation sets? What will the training set be used for? What will the validation set be used for? Select all correct statement(s)
a. The training data set is used to build the model, and the validation data is used to test the prediction accuracy of the model.
b. In this process, the model (built using the training data set) is used to make predictions with the validation data - data that were not used to fit the model. In this way we get an unbiased estimate of how well the model performs.
c. The data should be partitioned into training and validation sets because we need two sets of data: one to build the model that depicts the relationship between the predictor variables and the predicted variable, and another to validate the model's predictive accuracy.
d. The training data set is used to test the prediction accuracy of the model, and the validation data is used to build the mod
Answers
The correct statements are a and b. Statement d is incorrect as the training data set is used to build the model, not to test its prediction accuracy.
The data should be partitioned into training and validation sets because we need two sets of data: one to build the model that depicts the relationship between the predictor variable(s) and the predicted variable, and another to validate the model's predictive accuracy. The training data set is used to build the model, and the validation data set is used to test the prediction accuracy of the model. In this process, the model (built using the training data set) is used to make predictions with the validation data - data that were not used to fit the model. In this way, we get an unbiased estimate of how well the model performs. Therefore, the correct statements are a and b. Statement d is incorrect as the training data set is used to build the model, not to test its prediction accuracy.
Your answer: a and b are the correct statements.
a. The training data set is used to build the model, and the validation data is used to test the prediction accuracy of the model.
b. In this process, the model (built using the training data set) is used to make predictions with the validation data - data that were not used to fit the model. In this way, we get an unbiased estimate of how well the model performs.
c. The data should be partitioned into training and validation sets because we need two sets of data: one to build the model that depicts the relationship between the predictor variables and the predicted variable, and another to validate the model's predictive accuracy.
Learn more about model here:
https://brainly.com/question/29810500
#SPJ1
what it the answer to 1 ÷ 4 1/2=
Answers
Answer:
2/9 or 0.22222
Step-by-step explanation:
Your answer should be at 50 or more words. You imagine that your tutor is asked to record the \D, student name, date of birth, home address and phone number of every student in your tutorial and then email the spreadsheet to the unit convenor. What problems might arise? Note: there are around 120 students in this, unit and several tutors. You must start a thread before you can read and reply to other threads
Answers
There are several potential problems that might arise if a tutor is asked to record personal information such as student names, dates of birth, home addresses, and phone numbers for a large number of students and then email the spreadsheet to the unit convenor.
One major concern is the security and privacy of the students' personal information.
There are logistical challenges involved in managing and organizing the large amount of data.
One major concern is the security and privacy of the students' personal information. Emailing a spreadsheet containing sensitive data poses a risk of unauthorized access, interception, or data breaches. If the spreadsheet falls into the wrong hands, it could lead to identity theft, privacy violations, or misuse of personal information. Additionally, there is the issue of compliance with data protection regulations, such as the General Data Protection Regulation (GDPR), which requires the protection of personal data and imposes strict guidelines on its handling.
Moreover, there are logistical challenges involved in managing and organizing the large amount of data. Ensuring accuracy and maintaining data integrity becomes increasingly difficult with a higher number of students and multiple tutors. There may be instances of data entry errors, missing information, or duplication, which can lead to confusion and inaccuracies in student records.
To address these problems, it is important to establish secure data management protocols, such as using encrypted file transfer methods or secure file sharing platforms. Implementing strict access controls and limiting the number of individuals handling and transmitting the data can help mitigate the risks. It is also essential to comply with relevant privacy laws and regulations and provide clear guidelines to tutors on data protection and confidentiality. Regular data audits and reviews can help identify and rectify any potential issues in the data management process.
Learn more about data integrity here:
https://brainly.com/question/33539122
#SPJ11
A commodity was sold for 120.00 at a 20% loss on the cost. What is the price of the merchandise?
Answers
Answer:
$150
Step-by-step explanation:
CP = 100/(100 - L%) × SP
CP = 100/(100 - 20) × 120
CP = 100/80 × 120
CP = 5/4 × 120
CP = 5 × 30
CP = $150