Answers
The equation of the line in fully simplified slope-intercept form is \(y=\frac{1}{4} x-1\).
What is a slope intercept form?A line is defined by the equation y = mx + b, which is also known as the slope-intercept form. When the line is graphed, m represents the slope and b the point at which the line intersects the y-axis.
For calculating the slope, the formula used is \(m=\frac{x_{2} -x_{1} }{y_{2} -y_{1} }\)
From the graph we see that the points are (4,0) and (0,-1).
Substituting the points in the formula,
\(m=\frac{x_{2} -x_{1} }{y_{2} -y_{1} }\\m=\frac{-1-0}{0-4} \\m=\frac{-1}{-4} \\m=\frac{1}{4}\)
We know that, the equation of a line in point slope form, where (x₁, y₁) is the point and slope m is:
(y – y₁) = m(x – x₁)
Here, (x₁, y₁)= (4,0)
Substitute the value of m and any coordinate into the formula y−y₁=m(x−x₁)
\(y-0=\frac{1}{4} (x-4)\\y=\frac{1}{4} x-1\)
Therefore, the equation of the line in fully simplified slope-intercept form is \(y=\frac{1}{4} x-1\).
To learn more about the slope intercept form, visit:
https://brainly.com/question/9682526
#SPJ9
Related Questions
Find the volume of a pyramid with a square base, where the side length of the base is
10.6
in
10.6 in and the height of the pyramid is
12.3
in
12.3 in. Round your answer to the nearest tenth of a cubic inch.
Answers
Answer:
V = 460.68
Step-by-step explanation:
V=(lwh)/3
Volume = (1/3) * base area * height
In this case, the base of the pyramid is a square with a side length of 10.6 inches, so the base area can be calculated as:
Base area = side length * side length
Let's calculate the base area first:
Base area = 10.6 in * 10.6 in
Next, we'll substitute the values into the volume formula:
Volume = (1/3) * (10.6 in * 10.6 in) * 12.3 in
Calculating this expression will give us the volume of the pyramid. Rounding the answer to the nearest tenth of a cubic inch will provide the final result.
What is the output when the input is 0
Answers
Answer:
When the inputs are 1 and 0, the output is zero.
The diameter of Jacob's circular tabletop is 6 feet. What is the area, in square feet, of Jacob's tabletop?
Answers
Answer:
approximately 28.26 square feet
Step-by-step explanation:
The formula for the area of a circle is A = pi(r)^2. So, the radius is half of the diameter, meaning it's 3 feet. Then we square it to get 9, and multiply by pi, or 3.14. This leads us to the approximated answer of 28.26 square feet.
The area is:
28.27 square feet
Work/explanation:
Since the tabletop is circular, we use the formula for a circle's area, which is: \(\bf{A=\pi r^2}\).
We have the diameter, and to find the radius, we divide the diameter by 2, which gives us 6 ÷ 2 = 3 feet, so the radius of the tabletop is 3 feet.
Now, here's a diagram for you;
\(\setlength{\unitlength}{1cm}\begin{picture}(0,0)\thicklines\qbezier(2.3,0)(2.121,2.121)(0,2.3)\qbezier(-2.3,0)(-2.121,2.121)(0,2.3)\qbezier(-2.3,0)(-2.121,-2.121)(0,-2.3)\qbezier(2.3,0)(2.121,-2.121)(-0,-2.3)\put(0,0){\line(1,0){2.3}}\put(0.5,0.3){\bf\large 3\ ft}\end{picture}\)
Plug in the data:
\(\sf{A=\pi\times3^2}\)
\(\sf{A=\pi\times9}\)
\(\sf{A=28.27\:ft^2}\)
Hence, the area is 28.27 square feet.Measure of ∡5
(Hint: What theorem lets you compare ∡3 and ∡5?)


Answers
Answer:
mAngle5 = 52° by
Alternate Interior angles
Step-by-step explanation:
When you have a pair of parallel lines and a transversal (the line that crosses them both)
this set up makes 8 angles....ALL the angles are either the same measure or they add up to 180°. Literally, if you know the measure of ONE angle, you can find the measure of all 8 angles. Its only two different numbers for all 8.
So, for your problem the two angles are in between the parallel lines (interior) and on different sides of the tranversal (alternate). By the Alternate Interior Angle Theorem they are congruent. One of them is 52° so the other one is also 52°
there are 9 red markers, 5 blue markers, 14 yellow markers, and 8 green markers in a pencil box. A marker is chosen at random, replaced, then another is chosen. Find each probability.
P(yellow, then red)
P(blue, then green)
P(both red)
Answers
We will see that the probabilities are:
P(yellow, then red) = 0.1P(blue, then green) = 0.03P(both red) = 0.06How to find the probabilities?
First, the probability of getting a particular color of marker is given by the quotient between the number of markers of that color and the total number of markers
There are:
9 red markers.
5 blue markers.
14 yellow markers
8 green markers.
For a total of: 9 + 5 + 14 + 8 = 36.
a) P(yellow, then red)
First, the probability of getting a yellow marker is:
p = 14/36.
Then the probability of getting a red marker (notice that now there are 35 markers in total) is:
q = 9/35.
Then the joint probability is:
P(yellow, then red) = p*q = ( 14/36)*(9/35) = 0.1
b) P(blue, then green)
First, the probability of getting a blue marker is:
p = 5/36.
After, the probability of getting a green marker is:
q = 8/35.
So the joint probability is:
P(blue, then green) = (5/36)*(8/35) = 0.03
c) P(both red).
First, the probability of getting a red marker is:
p = 9/36
Now there are 8 red markers and 35 markers in total, so the probability of getting another red marker is:
q = 8/35
The joint probability is:
P(both red) = (9/36)*(8/35) = 0.06
If you want to learn more about probability:
https://brainly.com/question/251701
#SPJ1
the votes for Tigers outnumbered the votes for Lions by a ratio of 240 to 160. Describe the meaning of the statement and identify if its part to part or part to whole ratio
Answers
The ratio of 240 to 160 is part to part ratio.
What is mean by Ratio?
A ratio indicates how many times one number contain in another number. The ratio of two number is written as x : y, which is equivalent to x/y. Where, x and y are individual amount of two quantities. And, Total quantity gives after combine as x + y.
Given that;
The votes for Tigers outnumbered the votes for Lions by a ratio of 240 to 160.
⇒ 240 : 160.
Now,
We know that,
The ratio of part to part will be two different objects.
And, The ratio of part to whole will be the ratio of object to whole object.
Here, The ratio is given as;
⇒ 240 to 160.
⇒ 240 : 160
And, 240 > 160
So, The ratio is part to part ratio.
Thus, The ratio of 240 to 160 is part to part ratio.
Learn more about the ratio visit:
brainly.com/question/12024093
#SPJ1
The length of a rectangle is twice its width. Find its lenght and width, if its perimeter is 7 1/3 cm.
Answers
The length of the rectangle is twice its width. If its perimeter is 7 1/3 cm, its length will be 22/9 cm, and the width is 11/9 cm.
Let's assume the width of the rectangle is "b" cm.
According to the given information, the length of the rectangle is twice its width, so the length would be "2b" cm.
The formula for the perimeter of a rectangle is given by:
Perimeter = 2 * (length + width)
Substituting the given perimeter value, we have:
7 1/3 cm = 2 * (2b + b)
To simplify the calculation, let's convert 7 1/3 to an improper fraction:
7 1/3 = (3*7 + 1)/3 = 22/3
Rewriting the equation:
22/3 = 2 * (3b)
Simplifying further:
22/3 = 6b
To solve for "b," we can divide both sides by 6:
b = (22/3) / 6 = 22/18 = 11/9 cm
Therefore, the width of the rectangle is 11/9 cm.
To find the length, we can substitute the width back into the equation:
Length = 2b = 2 * (11/9) = 22/9 cm
So, the length of the rectangle is 22/9 cm, and the width is 11/9 cm.
For more information on the Perimeter of the Rectangle, click:
https://brainly.com/question/13757874
Gloria is categorizing triangles based on their properties. The side lengths of the triangles are listed below. Triangle 1: 3 cm, 4 cm, 5 cm Triangle 2: 5 cm, 5 cm, 7 cm Triangle 3: 6 cm, 7 cm, 9 cm Triangle 4: 8 cm, 8 cm, 8 cm She places the triangles into 3 different groups: scalene, isosceles, and equilateral. Which pair of triangles would Gloria put in the same group?
A. 1 and 2 B. 1 and 3 C. 2 and 3 D. 2 and 4
Answers
Triangle 1 is considered scalene as it has 3 sides all different sizes
And the same applies for triangle 3
Can you please solve and see which one is a function and which one is not a function

Answers
For each relation, we would determine whether or not it is a function as follows;
Relation 1 is: B. not a function
Relation 2 is: B. not a function.
Relation 3 is: B. not a function
Relation 4 is: A. a function.
How to determine the relations that represent functions?In Mathematics, a function is generally used for uniquely mapping an independent value (domain or input variable) to a dependent value (range or output variable).
This ultimately implies that, an independent value (domain) represents the value on the x-coordinate of a cartesian coordinate while a dependent value (range) represents the value on the y-coordinate of a cartesian coordinate.
Based on relations 1, 2, and 3, we can logically deduce that they do not represent a function because their independent value (domain) has more than one dependent value (range).
Read more on function here: brainly.com/question/3632175
#SPJ1
Imagine that such a die is rolled twice in succession and that the face values of the two rolls are added together. This sum is recorded as the outcome of a single trial of a random experiment. what is the probability of The sum is greater than 6.
Answers
Answer:
13/18
Step-by-step explanation:
We know that there are 36 outcomes.
1,1 1,2 1,3 1,4 1,5 1,6
2,1 2,2 2,3 2,4 2,5 2,6
3,1 3,2 3,3 3,4 3,5 3,6
4,1 4,2 4,3 4,4 4,5 4,6
5,1 5,2 5,3 5,4 5,5 5,6
6,1 6,2 6,3 6,4 6,5 6,6
so that is,
26/36
= 13/18
pls vote mine as brainiest
What is the total number of pitchers of iced tea that can be made with 24 tea bags?
A. 5 pitchers
B. 6 pitchers
C. 7 pitchers
D. 8 pitchers

Answers
Answer:
24/4= 6 pitchers
it takes four tea bags to make a pitcher of tea, so you divide 24 by 4 to see how many pitchers it takes
your answer is B
Write 64 % as a decimal and as a simplified fraction.
O 6.4 and 64/100
O 0.64 and 64/100
O 6400 and 6400/1
0.64 and 16/25
Answers
Answer:
b. 0.64 and 64/100
Step-by-step explanation:
hope this helps!!
Answer: B.) 0.64 and 64/100
Step-by-step explanation:
A percentage is x/100
For example, 4% = 4/100.
So 64% = 64/100
64/100 = 0.64
The sum of two numbers is 56. Their difference is 24. Find the two numbers.
Answers
Step-by-step explanation:
Assume the two numbers as X and Y and solve the equation.
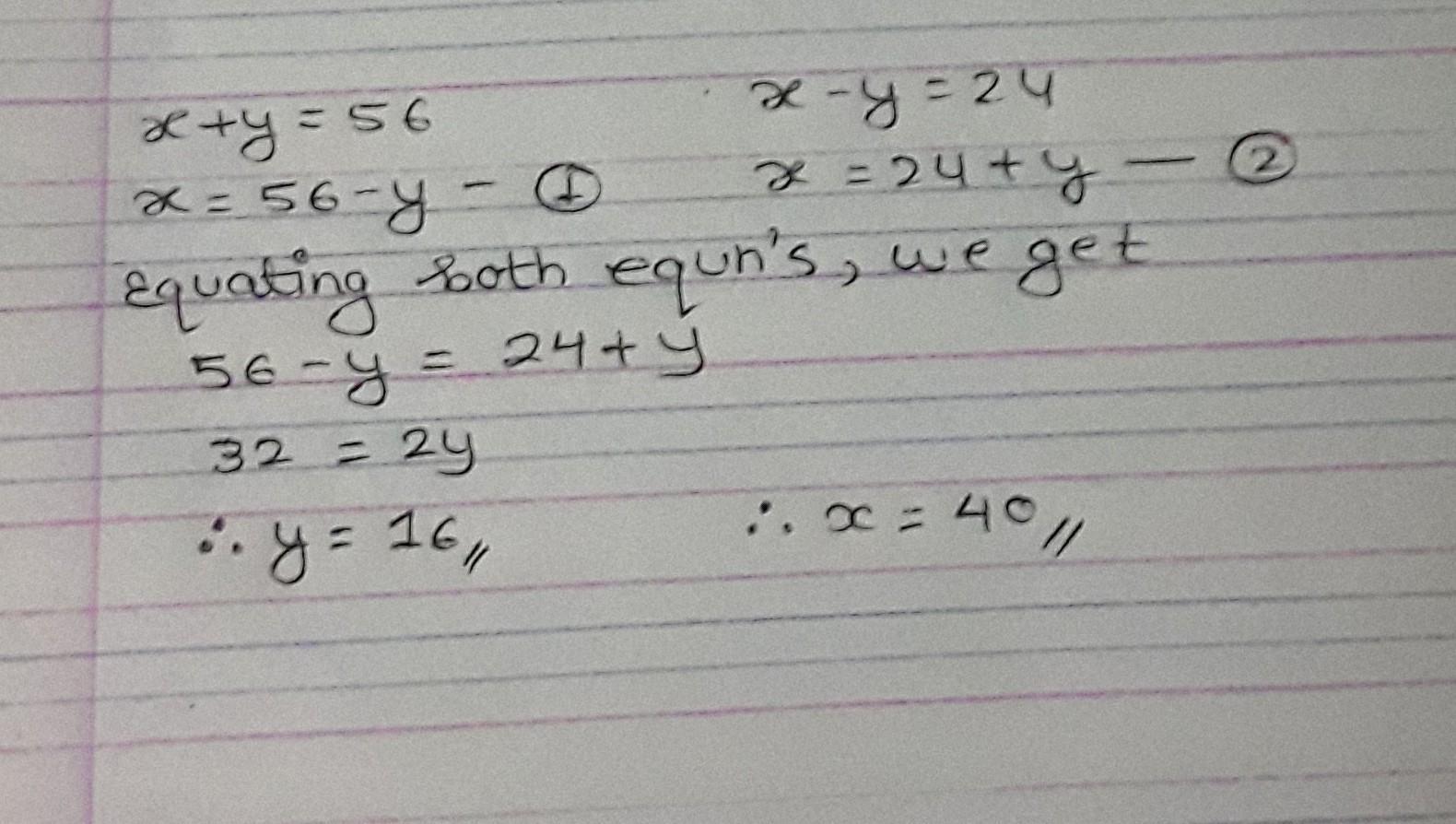
Manny grows vegetables in a community garden.
His part of the garden is a rectangular area that is 6 yards long and 5 1/3 yards wide. What is the area of Manny’s garden? Be sure to include units in your answer.
Answers
Answer:
32 yards (squared)
Step-by-step explanation:
Length x width = area (LxW=A)
Step 1:
Length = 6 yards
Width = 5 1/3 yards
Step 2:
Multiply 6 x 5 1/3 because 6 is the length, 5 1/3 is the width, and LxW=A.
6 x 5 1/3 = 32 yards (squared)
1/12 + 7/9
Help me my teacher would get mad if I get it wrong...
Answers
Answer:
\( \displaystyle \: \frac{1}{12} + \frac{7}{9} \)
Multiples of 12={12,24,36,48,60}Multiples of 9={9,18,27,36,45,54}The least common multiple=36So,
\( \displaystyle{ \frac{1}{12} = \frac{1 \times 3}{12 \times 3} = \frac{3}{36} }\)
\(\displaystyle{ \frac{7}{9} = \frac{7 \times 4}{9 \times 4} = \frac{28}{36} }\)
Now,
\(\displaystyle{ \frac{3}{36} + \frac{28}{36} = \frac{3 + 28}{36} = \frac{31}{36} }\)
Unless specified, all approximating rectangles are assumed to have the same width. Evaluate the upper and lower sums for f(x) = 1 + cos - SXST, with n = 3, 4, and 6. Illustrate each case with a sketch similar to the figure shown below.
Answers
The upper and lower sums for f(x) = 1 + cos - SXST, with n = 3, 4, and 6 is 10.1913798 and 10.19913798.
What is upper and lower sums?
Using rectangles that are both enscribed in and circumscribed by a curve, we may approximate the area under a curve. The total area of the rectangles that are inscribed is the lower sum, while the total area of the rectangles that are circumscribed is the higher sum.
\($n=6: \quad \Delta x=\frac{2 \pi}{6}$\)
\(\begin{aligned}& \text { Lower sum }=\frac{2 \pi}{6}\left[f(-\overline{4})+f\left(-\frac{2 \pi}{3}\right)+f\left(-\frac{\pi}{3}\right)+f(0)+f\left(\frac{\pi}{3}\right)+f\left(\frac{2 \pi}{3}\right)\right] \\& c_6=\frac{2 \pi}{6}[1+1.5+1.8660256+2+1.8660254+1.5] \\& c_6=10.1913798\end{aligned}\)
upper sum:
\(\begin{aligned}& =\frac{2 \pi}{6}\left[f\left(-\frac{2 \pi}{3}\right)+f\left(-\frac{\pi}{3}\right)+f(0)+f\left(\frac{\pi}{3}\right)+f\left(\frac{2 \pi}{3}\right)+f(\pi)\right] \\R_6 & =\frac{2 \pi}{6}[1.5+1.8660254+2+1.8660254+1.5+1] \\R_6 & =10.1913798]\end{aligned}\)
To learn more about upper and lower sums visit:https://brainly.com/question/17019015
#SPJ4
What is the slope of the line that passes through the points (4, 7) and (5,8)?
Write your answer in simplest form.
Answers
Answer:
1
Step-by-step explanation:
Use the coordinates of the points to determine the slope
slope = Δy/Δx = (8-7)/(5-4) = 1
Find the volume V of the solid obtained by rotating the region bounded by the given curves about the specified line. y = 1 + sec(x), −π 3 ≤ x ≤ π 3 , y = 3; about y = 1
Answers
Using the washer method, the volume is given by the integral
\(\displaystyle\pi\int_{-\pi/3}^{\pi/3}\bigg((3-1)^2-((1+\sec x)-1)^2\bigg)\,\mathrm dx=2\pi\int_0^{\pi/3}(4-\sec^2x)\,\mathrm dx\)
where 3 - 1 = 2 is the distance from y = 3 to the axis of revolution, and similarly (1 + sec(x)) - 1 = sec(x) is the distance from y = 1 + sec(x) to the axis. The integrand is symmetric about x = 0, so the integral "folds" in on itself, and the integral from -π/3 to π/3 is twice the integral from 0 to π/3.
So the volume is
\(\displaystyle2\pi\int_0^{\pi/3}(4-\sec^2x)\,\mathrm dx=2\pi(4x-\tan x)\bigg|_0^{\pi/3}=\boxed{\dfrac{8\pi^2}3-2\pi\sqrt3}\)
what is value of 4/5 - 2/3
Answers
Answer: 2/15
You have to get the denominators to the same number which would be 15
What is the product of the 4 x and the 3 x cubed y squared minus 2 x y cubed?
Answers
Answer: 170678
Step-by-step explanation:
try it and you'll see.
Does coordinates s or coordinate t represent a greater number in the following
parallelogram?
(-2,3)
(s, -1)
(0, -1)
(t, 3)
Answers
Thus, t has a greater value than s for the co-ordinates (s, -1) and (t, 3).
How to analyze points of an axis for a two dimensional entity?
We can use the fact that both points on the x-axis to compare the values of s and t for the provided parallelogram. As a result, each point that is closest to the x coordinate reflects a higher value than its equivalent counterparts.
Given, the co-ordinates of the parallelogram are: (-2, 3), (s, -1), (0, -1),
(t, 3).
Also, the co-ordinates of the parallelogram are also shown in the figure below.
To compare for the values of s and t for the given parallelogram,
we can analyze that both s and t represent points on the x-axis, therefore any point that stands rightmost with the x co-ordinate represents a higher value than the corresponding counterparts.
Therefore, t has a greater value than s for the co-ordinates (s, -1) and (t, 3), since t is on the right side from s.
To learn more about this, tap on the link below:
https://brainly.com/question/16882931
#SPJ13

The mean weight of an adult is 6565 kilograms with a standard deviation of 1313 kilograms. If 9292 adults are randomly selected, what is the probability that the sample mean would be greater than 62.762.7 kilograms
Answers
Answer: 0.9554
Step-by-step explanation:
Let \(\overline{X}\) be the sample mean.
Given: Mean weight\((\mu)\) of an adult is 65 kilograms with a standard deviation\((\sigma)\) of 13 kilograms.
Sample space = 92
The probability that the sample mean would be greater than 62.7 kilograms:
\(P(\overline{X}>62.7)=P(\dfrac{\overline{X}-\mu}{\dfrac{\sigma}{\sqrt{n}}}>\dfrac{62.7-65}{\dfrac{13}{\sqrt{92}}})\\\\=P(Z>-1.70)\\\\=P(Z<1.70)\ \ \ \[P(Z>-z)=P(Z<z)]\\\\=0.9554\)[ By p-value table]
Hence, the required probability= 0.9554
3x+5=6(x+24)
What does x= please help! I need the answer ASAP
Answers
Answer:
- 139/-3
Step-by-step explanation:
i took the test
6. A high school graduate works fulltime. She needs to borrow $1,500 to
attend the local junior college, but she won't be able to pay it back for
2
years. Calculate how much she will have to pay back with these two
loan plans. Which plan should she choose? Justify your answer,
Bank A: Simple interest, 18 percent per year
Bank B: Compound interest, 12 percent per year

Answers
Answer:
I think you would have to multiply 1,500 by 12 and also by 18 to figure it out.
Step-by-step explanation:
" "
Angles A and B are supplementary. Determine the measure of angle A if the measure of angle B is 121.3°.
238.7°
31.3°
53.7°
58.7°
Answers
The required measure of angle m ∠A is 58.7° which is the correct answer would be an option (D).
What are supplementary angles?The supplementary angles are defined as when pairing of angles addition to 180° then they are called supplementary angles.
Angles A and B are supplementary.
We have been given that m angle ∠B= 121.3°,
To determine the measure of angle A if the measure of angle B is 121.3°.
As per the property supplementary angles,
m∠A + m ∠B = 180°
m∠A + 121.3 ° = 180°
m ∠A = 180° - 121.3°
m ∠A = 58.7°
Therefore, the required measure of angle m ∠A is 58.7°
Learn more about supplementary angles here:
brainly.com/question/3027144
#SPJ1
24°
Solve for c.
= [?]°
C =
60% C
Enter
![24Solve for c.= [?]C =60% CEnter](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/18LkggivbR7cp80IPjukTXssaWPx5XaX.png)
Answers
Answer:
96°
Step-by-step explanation:
You want the value of angle C in the diagram with two parallel lines and a triangle between them.
Angle sum theoremThe sum of angles in a triangle is 180°, so the missing angle in the triangle is ...
180° -60° -24° = 96°
Alternate interior anglesAngle C and the one we just found are alternate interior angles with respect to the parallel lines and the transversal that forms those angles. As such, they are congruent:
C = 96°
<95141404393>
Salve this proportion 15/35=g/7
Answers
A direct variation includes the points (2,18) and (n,9). Find n?
Answers
The value of the n is 1
In a direct variation, the relationship between two variables is of the form y = kx, where k is a constant of proportionality.
To find the constant of proportionality k in this problem, we can use the fact that the given points satisfy the equation for direct variation.
(2,18) is one of the given points, so we can substitute these values into the equation y = kx and solve for k:
18 = k(2)
k = 18/2
k = 9
Now that we have found the value of k, we can use it to find n when y = 9:
9 = 9n
n = 1
Therefore, the value of n is 1.
Learn more about coordinates here:
https://brainly.com/question/20282507
#SPJ1
through:(-1,-5) and (0,4)
Write the slope intercept form of the equation with a explanation of how you got the answer
Answers
P/s: The slope intercept form of the equation is m
Answer: 9
ok done. Thank to me :>

what is the difference between radical and rational exponents
Answers
Answer:
there the same
Step-by-step explanation:
