Write the equation of a circle that has a center at the point (-3, 6) and passes through the point (9, 1).
SOMEONE HELP I WILL MARK BRAINLIEST!!!!!
Oh and put in a link and I will report you, then slaughter you <3
Answers
The equation of the circle with a center at (-3, 6) and passing through the point (9, 1) is (x + 3)^2 + (y - 6)^2 = 169.
To write the equation of a circle with a center at the point (-3, 6) and passing through the point (9, 1), we can use the general equation of a circle: (x - h)^2 + (y - k)^2 = r^2, where (h, k) is the center of the circle, and r is the radius.
1. Identify the center (h, k) as (-3, 6).
2. Calculate the radius using the distance formula between the center and the given point (9, 1):
r = √((x2 - x1)^2 + (y2 - y1)^2)
r = √((9 - (-3))^2 + (1 - 6)^2)
r = √((12)^2 + (-5)^2)
r = √(144 + 25)
r = √169
r = 13
3. Substitute the values of h, k, and r into the equation of a circle:
(x - (-3))^2 + (y - 6)^2 = 13^2
(x + 3)^2 + (y - 6)^2 = 169
So, the equation of the circle with a center at (-3, 6) and passing through the point (9, 1) is (x + 3)^2 + (y - 6)^2 = 169.
To know more about equation, visit:
https://brainly.com/question/29657983#
#SPJ11
Related Questions
Perform the indicated operations. Write the answer in standard form, a+bi.
-5-7i / 13+4i
Answers
Answer:
\(thank \: you\)

Find the base area (B), lateral area (L) and surface area (S) of the solid. Round to the
nearest tenth, if necessary.
10.4 cm
B = 96
L =
12 cm
S=
12 cm
12 cm
8 cm
cm²
cm²
cm²

Answers
The base area, the lateral area and the surface area of the prism are 124.8 cm², 288 cm² and 412.8 cm², respectively.
How to compute the base area, the lateral area and the surface area
In this problem we need to compute three kinds of areas in a prism with a triangular base. The base area, that is, the sum of the areas of the two triangles, the lateral area, that is, the sum of the areas of the three rectangles and the surface area, that is, the sum of the base and lateral areas.
The area formulas of the triangle and rectangle are, respectively:
Triangle
A = 0.5 · b · h
Rectangle
A = b · h
Where:
A - Area, in square centimeters.b - Width, in centimeters.h - Height, in centimeters.Now we proceed to determine each kind of area:
Base area
A = 2 · 0.5 · (12 cm) · (10.4 cm)
A = 124.8 cm²
Lateral area
A = 3 · (8 cm) · (12 cm)
A = 288 cm²
Surface area
A = 124.8 cm² + 288 cm²
A = 412.8 cm²
To learn more on surface areas: https://brainly.com/question/29298005
#SPJ1
What is a variable in a question?
Answers
Answer: A variable is an object, event, idea, feeling, time period, or any other type of category you are trying to measure.
A variable is a characteristic that can be measured and that can assume different values. Height, age, income, province or country of birth, grades obtained at school and type of housing are all examples of variables. Variables may be classified into two main categories: categorical and numeric
Answer:
a variable (as the letters a, b, c, y, etc.) is considered a missing number within a mathematical problem
what is the value of k? ____ units

Answers
Answer:
2
Step-by-step explanation:
Corresponding sides are proportional in these similar triangles.
__
short side/long side = k/4 = 4/8
k = 4(4/8) . . . . multiply by 4
k = 2
_____
Additional comment
The lengths of the hypotenuses can be found the same way, or using the Pythagorean theorem. Using side ratios, we have ...
l² = k(k+8) = 2(10) = 20 . . . . from MN/MO = ML/MN
l = 2√5
m² = 8(8+2) = 80 . . . . from LN/LO = LM/LN
m = 4√5
The similarity statements are ...
ΔLMN ~ ΔLNO ~ ΔNMO
solve for x using parallel lines and angles
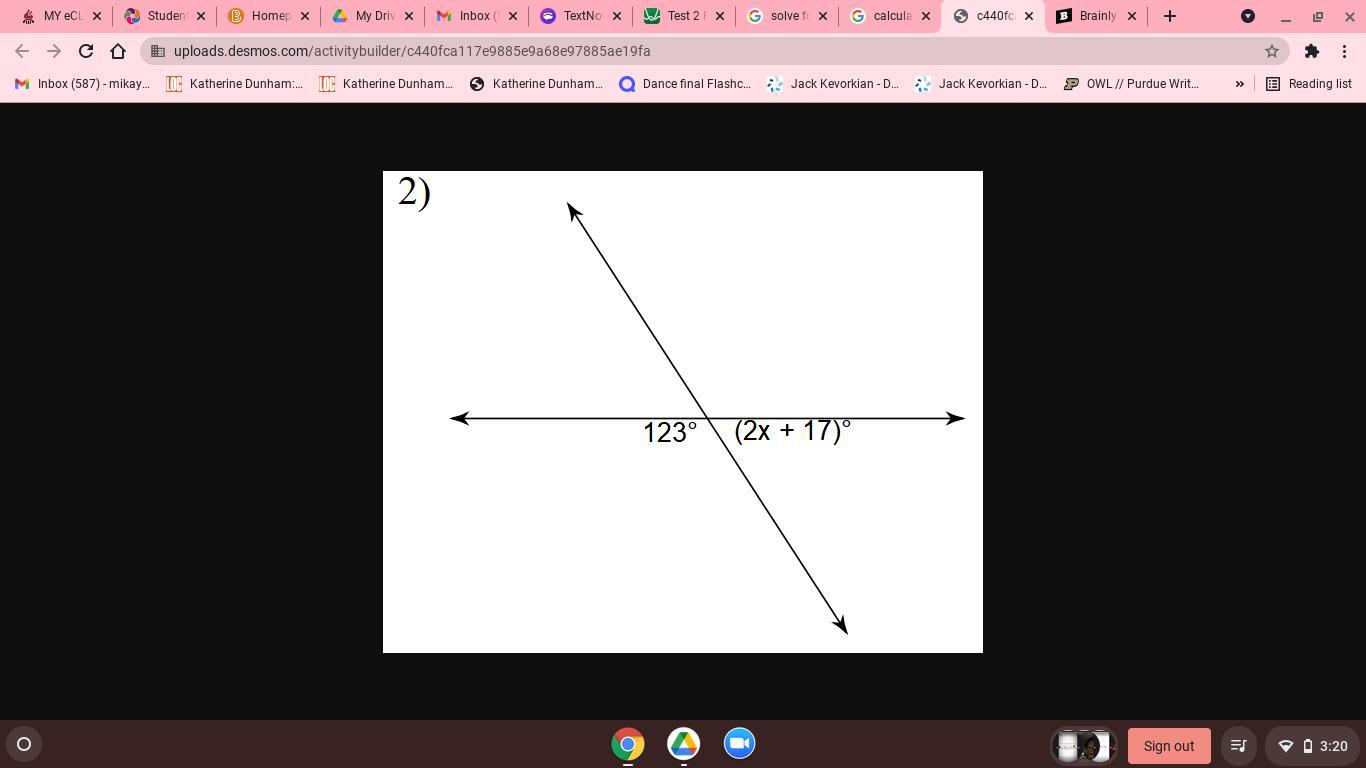
Answers
Answer:
x = 20
Step-by-step explanation:
The 2 given angles are adjacent on a straight line and sum to 180° , then
123 + 2x + 17 = 180
140 + 2x = 180 ( subtract 140 from both sides )
2x = 40 ( divide both sides by 2 )
x = 20
6: Find the nature of the quadratic equation x2 + 8x + 16 = 0. 5: Find the nature of the solutions of the quadratic equation x2 - 24x + 144 = 0. 7: Find the nature of the quadratic equation x2 - 25 = 0. 9: Quadratic formula determines ___________ solutions to the quadratic equation. 10: Identify the roots of the quadratic equation 2x2 + 5x + 3 = 0. SOMEONE PLEASE
Answers
Answer:
The quadratic equation x2 + 8x + 16 = 0 is a perfect square trinomial, which means it can be factored as (x+4)²=0. Therefore, the nature of the quadratic equation is a perfect square trinomial, and it has one real root with a multiplicity of 2.
The quadratic equation x2 - 24x + 144 = 0 can be factored as (x-12)²=0, which is also a perfect square trinomial. Therefore, the nature of the solutions is a perfect square trinomial, and it has one real root with a multiplicity of 2.
The quadratic equation x2 - 25 = 0 can be factored as (x+5)(x-5)=0, which means it has two real roots: x=5 and x=-5.
The quadratic formula determines the solutions to the quadratic equation in terms of its coefficients. The formula is x = (-b ± √(b²-4ac)) / (2a), where a, b, and c are the coefficients of the quadratic equation ax² + bx + c = 0.
The roots of the quadratic equation 2x2 + 5x + 3 = 0 can be found by factoring it as (2x+3)(x+1)=0, which means the roots are x=-3/2 and x=-1.
Step-by-step explanation:
Match the plot with a possible description of the sample.
60 70 80 90 100
Choose the correct answer below
A. Wait time (in minutes) for a sample of doctors offices
B.Ages (in years) of a sample of residents of a retirement home.
C. Highest yearly temperatures (F) for a sample of deserts.
D. Time (in hours_ spent watching TV in a day for a sample of teenagers.
Answers
Ages (in years) of a sample of retirement home inhabitants is option B. For the lowest wait time, the maximum frequency is anticipated to be right-skewed. A desert cannot have a maximum annual temperature of 60°F, and it is not conceivable to watch 60+ hours of TV in a single day.
Residents of senior living facilities are typically 84 years old. While there are many couples in these communities, the majority of people who live in independent living are women. Some people move in at or near the minimum age (often around 65), but most people do so between the ages of 75 and 84. Residents come from all different backgrounds.
Many people are choosing senior living in a community environment, including teachers, nurses, small business owners, big business CEOs, university professors, housewives, lawyers, engineers, musicians, and more. Current residents will attest that the rich diversity of origins fosters amazing interactions and relationships. And contrary to popular belief, the majority of residents of independent living are quite active.
To learn more about sample visit : brainly.com/question/24261687
#SPJ4
Correct Question:
Match the plot with a possible description of the sample.
60 70 80 90 100
Choose the correct answer below
A. Wait time (in minutes) for a sample of doctors offices
B. Ages (in years) of a sample of residents of a retirement home.
C. Highest yearly temperatures (F) for a sample of deserts.
D. Time (in hours_ spent watching TV in a day for a sample of teenagers.

Given: AE= 7 5/8cm, AB=BC, CD= 1/2cm, and DE is 3/8 more than AB. What is the length of DE?
Answers
Answer:
Length of DE = 2.90 (Approx)
Step-by-step explanation:
Given:
AE = 7\(\frac{5}{8}\)cm = 61 / 8 cm = 7.625 cm
AB = BC
CD = 1/2 cm = 0.5 cm
DE is 3/8 more than AB
Find:
Length of DE
Computation:
Assume;
AB = BC = x
So,
DE = x + 3/8(x) = [11 / 8]x = [1.375]x cm
AE = AB + BC + CD + DE
7.625 = x + x + 0.5 + [1.375]x
7.125 = 3.375 x
x = 2.1111 (Approx)
Length of DE = [1.375][2.111]
Length of DE = 2.90 (Approx)
Follow the directions to solve the system of equations by elimination.
8x + 7y = 39
4x – 14y = –68
Multiply the first equation to enable the elimination of the y-term.
Add the equations to eliminate the y-terms.
Solve the new equation for the x-value.
Substitute the x-value back into either original equation to find the y-value.
Check the solution.
The solution to the system of equations is?
Answers
Answer:
X= 1/2 Y= 5
Step-by-step explanation:
8x+7y=39-------------(1)--------×2
4x-14y= -68-----------(2)-------×1
16X + 14Y = 78--------(3)
4X- 14Y = -68----------(4)
Addy equation (4) and (3)
20X = 10
dividing bothsides by 20
20X/20= 10/20
X = 1/2
substitute the value of X into equation (1)
8X+7Y = 39
8(1/2)+7Y= 39
4+7Y = 39
7Y = 39-4
7Y = 35
dividing bothsides 7
7Y= 35/7
Y = 5
8 less than 3 times a number is at most 30
Answers
8 less than 3 times a number is at most 30 can be written as 8 < 3N ≤ 30
How to write and solve a word problem?A word problem is a mathematical exercise where significant background information on the problem is presented in ordinary language rather than in mathematical notation
Since 8 less than 3 times a number is at most 30
Let the number be N
Thus, 8 less than 3 times a number is at most 30 can be written as:
8 < 3×N ≤ 30
8 < 3N ≤ 30
Note: at most means less than or equal (≤)
Learn more about word problems on:
brainly.com/question/1781657
#SPJ1
The graph shows two linear functions, f and g. Which formula BEST represents g(x)?
A)g(x) = 2f(x)
B)g(x) = 3f(x)
C)g(x) = 1/2f(x)
D)g(x) = 3/2f(x)

Answers
Answer: C
g(x) = 1/2 f (x)
Step-by-step explanation:
Answer:
Step-by-step explanation:
c
ms salinas is packing lunches for a field trip. She is placing 15 sack lunches in each of 3 ice chests. Each sack lunch contains a sandwich, an apple, and a bag of potato chips. 40% of the sandwhiches an turkey sandwiches. How many of the sack lunches contain a turkey sandwhich
Answers
Answer:18
Step-by-step explanation:
Because 40% of 45 is 18
solve by factoring
\( {n}^{2} - 6n= 0\)
Please show all work!
Answers
Answer:
\(n=0,\\n=6\)
Step-by-step explanation:
Given \(n^2-6n=0\), we can factor out an \(n\) from each of the terms on the left side of the equation:
\(n(n-6)=0\)
Since we have two factors that multiply to zero, we can set each of them to zero and solve for \(n\), because zero multiplied by anything is equal to zero. Therefore, as long as either \(n\) or \(n-6\) is equal to zero, the other factor can be any real number and the equation would still hold true.
Therefore, we have the following cases:
\(\begin{cases}n=0,\\n-6=0\end{cases}\)
Solving, we get:
\(\begin{cases}n=0, n=\boxed{0}\\n-6=0, n=\boxed{6}\end{cases}\)
\(\\ \sf\longmapsto n^2-6n=0\)
Take n common\(\\ \sf\longmapsto n(n-6)=0\)
Now
\(\\ \sf\longmapsto n=0\:or \:(n-6)=0\)
\(\\ \sf\longmapsto n=0\:or \;n=6\)
Hence roots of the equation are 0 and 6 .
More:-
We can solve it through Quadratic formula
\(\boxed{\sf x=\dfrac{-b\pm \sqrt{b^2-4ac}}{2a}}\)
Find the side length, b.
Round to the nearest tenth.
B=90°
a=6
c=7

Answers
Answer:
b = 9.2
Step-by-step explanation:
Using the Pythagorean theorem (in your case): \(a^{2} +c^{2} = b^{2}\)
Plug in your values and solve for x:
\(6^{2}+7^{2} =b^{2}\\36+49 =b^{2} \\85 = b^{2} \\b = \sqrt{85} \\b = 9.2\)
A baby gains about 15 pounds each month. About how much weight will the baby have gained after 6 months? a. About 7.5 pounds b. About 8.5 pounds C. About 9 pounds d. About 10.5 pounds
Answers
Answer:
I'm going to assume you meant 1.5 pounds and not 15 pounds each month.
Step-by-step explanation:
1.5*6=9
C
Answer:
around 90 pounds
Step-by-step explanation:
15×6
or 15+15+15+15+15+15 if multiplying is not your thing
A shop has a sale of 10% off all items in stock.If the original price of a dress is £70 what would be its sale price?
Answers
10% off means it is on sale for 90% of the original price ( 100% - 10% = 90%)
Multiply the price of the dress by 90%:
£70 x 0.90 = £63
The sale price is: £63
Lacey ate 3/8 of 2 pizzas. Tory ate 1/4 of 2 pizzas. Xander and Lexi ate 1/2 of 3 pizzas. If there were 3 equal-sized pizzas, what fraction of all the pizza is left?
Answers
1/4 is the fraction of all the pizza left
How to determine the fraction of all the pizza left?A fraction represents the parts of a whole or collection of objects e.g 3/4 shows that out of 4 equal parts, we are referring to 3 parts.
Given that:
Lacey ate 3/8 of 2 pizzas => 3/8 × 2 = 3/4
Tory ate 1/4 of 2 pizzas => 1/4 × 2 = 1/2
Xander and Lexi ate 1/2 of 3 pizzas => 1/2 × 3 = 3/2
And there were 3 equal-sized pizzas
Fraction of pizza left = Number of pizzas - fraction ate by Lacey - Fraction ate by Tory - Fraction ate by Xander and Lexi
Fraction of pizza left = 3 - 3/4 - 1/2 - 3/2 = 1/4
Therefore, the fraction of all the pizza is left is 1/4
Learn more about fraction on:
brainly.com/question/11562149
#SPJ1
Belinda is thinking about buying a house for $179,000. The table below shows the projected value of two different houses for three years:
Answers
Answer:
A function is a relation from a set A to a set B where the elements in set A only maps to one and only one image in set B. No elements in set A has more than one image in set B.
Part A :
If a function is linear, then the function values have equal differences.
If a function is exponential, the function values have equal ratios.
For car 1 :
36450 / 40,500 = 9/10
32805 / 36450 = 9/10
Values of car have equal ratios.
This is exponential function.
For car 2 :
39000 - 42000 = -3000
36000 - 39000 = -3000
Values of car have equal differences
This is linear function.
Part B :
The initial value of car is 45,000.
For car 1 :
f(1) = 40,500, f(2) = 36,450, ............
For car 2 :
f(1) = 42,000, f(2) = 39,000, ..........
Part C :
For car 1 :
f(13) = = 11438.396
For car 2 :
f(13) = = 6000
There is a significant difference in the values of the car after 13 years. The value of the car 1 is greater.
Hence the value of the car 1 is described by an exponential function and that of car 2 by linear function. The value of car 1 is greater after 13 years.
Step-by-step explanation:
Graph the function.
For the function whose graph is shown below, which is the correct formula for the function?

Answers
Answer:
\(\displaystyle{y=-3x-1}\)
Step-by-step explanation:
I have two methods: standard-learning which will explain overall mathematically - basically formula, etc. - while the other one trick-tips method will rely on choices rather mathematical calculations but with explanation on why and how.
Standard-LearningFirst, let’s pick two points that are integers since they are easily to be found via graphs. We see that (-1,2) and (0,-1) is a part of the graph so now we finally have picked two points for our calculations.
When we have finally picked two points, we will be using them for slope calculation. This part is crucial for finding an equation of a line because a line has to contain slope in its equation.
To calculate the slope, we use rise over run formula which is:
\(\displaystyle{\dfrac{\Delta y}{\Delta x} = \dfrac{y_2-y_1}{x_2-x_1}}\)
Note that \(\displaystyle{\Delta}\) is delta - in both mathematic and physics, it means changes in.
So, we will be using those two points that we have picked to substitute in the slope formula. Let’s determine that \(\displaystyle{(x_2,y_2)=(-1,2)}\) and \(\displaystyle{(x_1,y_1)=(0,-1)}\).
Therefore, our slope will be:
\(\displaystyle{m=\dfrac{2-(-1)}{-1-0}}\\\\\displaystyle{m=\dfrac{2+1}{-1}}\\\\\displaystyle{m=-3}\)
Next, find the y-intercept. From the graph, we see that the graph intercepts at (0,-1) which is y-intercept so we will only use y-value. Hence, b = -1.
From the slope-intercept form:
\(\displaystyle{y=mx+b}\)
Substitute m (slope) = -3 and b (y-intercept) = -1. Hence, the equation of line is:
\(\displaystyle{y=-3x-1}\)
Fast Way (Trick-Tips)Relying on choices and knowledge of graph, notice that there are slopes of 3 and -3.
Keep in mind that if slope is negative, it will decrease down and if slope is positive, it will increase up.
Therefore, cut off all choices with positive slopes which are 1 and 3. We are now left with 2 and 4.
Next, look at the graph and tell its y-intercept. It intercepts y at y = -1 so we take value of -1.
So choice 4 is cut off and now we have choice 2 as the answer.
Learn More:
https://brainly.com/question/27514958 - Find the line equation with given points
Harry took out a loan from the bank. the variable ddd models harry's remaining debt (in dollars) ttt months after he took out the loan. d=-200t 9000d=−200t 9000d, equals, minus, 200, t, plus, 9000 how much does harry pay back each month?
Answers
Answer:
Harry has a loan of $9000 in total. Harry obtained a loan from the bank. Explanation Harry's remaining debt, expressed in dollars, is modeled as a function of time t, expressed in months, by the function D(t). The role is played by, This function can be used to determine that $200 is being subtracted each month from the function, meaning Harry is paying $200 toward his loan. Harry has not yet made any payments, therefore we may set t=0 to obtain the total amount of his solo. Therefore, the value of D(t) will reveal the loan's net amount. Harry's borrowing, therefore, equals to $9000.
HELP HELP HELP HELP HELP HELP

Answers
Step-by-step explanation:
You can take the numerator as one factor and 1/denominator as another.
Just an example:
a(x + 2) and 1/(a(x - 1)), with a rational value of a ≠ 0.Let a = 1, then the following product will give what we have
(x + 2) × 1/(x - 1) = (x + 2)/(x - 1)Farmer Josh has a pen full of chickens and pigs. One day he looks out and counts 17 heads ans 52 feet. How many chickens and pigs are in the pen?
Answers
The number of chickens and pigs in the pen are 8 and 9 respectively.
How to find the number of chickens and pigs in the pen?Farmer Josh has a pen full of chickens and pigs. One day he looks out and counts 17 heads and 52 feet.
The number of chickens and pigs that are in the pen is as follows:
Using equation,
let
x = number of chickens
y = number of pigs
Therefore,
x + y = 17
Recall chicken has 2 legs and pigs has 4 legs.
Hence,
2x + 4y = 52
Combine the equation
x + y = 17
2x + 4y = 52
multiply equation(1) by 2
2x + 2y = 34
2x + 4y = 52
subtract equation(1) from equation(2)
2y = 18
y = 18 / 2
y = 9
Let's find x
x = 17 - 9
x = 8
Therefore,
number of chickens = 8
number of pigs = 9
learn more on equation here: https://brainly.com/question/22931914
#SPJ1
PLEASE HELP ASAP!
:))

Answers
Answer: The converse of this theorem is also true; that is, if two lines n and m are cut by a transversal so that the alternate interior angles are congruent, then n║m.
Step-by-step explanation:
What does it mean converse in geometry?
The converse of a statement is formed by switching the hypothesis and the conclusion. The converse of "If two lines don't intersect, then they are parallel" is "If two lines are parallel, then they don't intersect." The converse of "if p, then q" is "if q, then p."
So, in the figure below, if we can choose n║m, then ∠1≅∠2
Since n║m , by the corresponding Angles Postulate,
∠1≅∠2.
Therefore, by the definition of congruent angles,
m∠1=m∠2
Since ∠1 and ∠2 form a linear pair, they are supplementary, so
m∠1+m∠2=180°.
Therefore, the converse of this theorem is also true; that is, if two lines n and m are cut by a transversal so that the alternate interior angles are congruent, then n║m.
Learn about more information https://brainly.in/question/14313548
#SPJ9
A cylinder has a radius of 16 inches. Its volume is 13,665. 28 cubic inches. What is the height of the cylinder?
Use ≈ 3. 14 and round your answer to the nearest hundredth
Answers
The height of the cylinder is 17.00 inches, under the given condition that radius of the cylinder is 16 inches, volume is 13,665. 28 cubic inches and have to round the answer to the nearest hundred.
Therefore, the volume of a cylinder is given by V = πr²h
Here,
V= volume of the cylinder,
r= radius of the cylinder
h= height
Given that the radius of the cylinder is 16 inches and its volume is 13,665.28 cubic inches, then we can proceed to evaluate the height of the cylinder
V = πr²h
h = V / (πr²)
h = 13665.28 / (π(16)²)
h = 13665.28/ 3.14 x (256)
h = 13665.28/ 803.8
h = 17.00 inches
Then, the height of the cylinder is approximately 17.00 inches.
To learn more about volume
https://brainly.com/question/27710307
#SPJ4
f(x) = 3(0.5)* transformation?
Answers
Answer: Vertical stretch by a factor of 3.
A snow globe is made out of regular right triangular prism that is inscribed in hemisphere with radius 12cm. help a designer to find the dimensions of maximum volume prison. state the exact answer.
Note: Find the dimensions of the prism for the case when the triangular base is on the grand circle of the hemisphere.
Answers
The maximum volume of the prism is 1728 cubic centimeters.
To find the dimensions of the prism with maximum volume, we need to consider the relationship between the volume of the prism and its dimensions.
Let's assume the base of the right triangular prism is an isosceles right triangle with legs of length 'a'. The height of the prism will be 'h'. The prism is inscribed in a hemisphere with a radius of 12 cm.
First, let's determine the relationship between 'a' and 'h'. Since the base of the prism is on the great circle of the hemisphere, the hypotenuse of the triangular base is equal to the diameter of the hemisphere, which is twice the radius. Therefore, the hypotenuse of the base is 2 * 12 = 24 cm.
By using the Pythagorean theorem, we can find 'a':
a^2 + a^2 = 24^2
2a^2 = 576
a^2 = 288
a = √288
Now, let's find the height 'h' of the prism. The height 'h' is equal to the radius of the hemisphere, which is 12 cm.
Therefore, the dimensions of the prism for maximum volume are:
Base length (a) = √288 cm
Height (h) = 12 cm
To find the maximum volume, we can use the formula for the volume of a right triangular prism:
Volume = (1/2) * a^2 * h
Substituting the values, we get:
Volume = (1/2) * (√288)^2 * 12
= (1/2) * 288 * 12
= 1728
Hence, the maximum volume of the prism is 1728 cubic centimeters.
for such more question on volume
https://brainly.com/question/6204273
#SPJ8
A right triangle has a hypotenuse of length 3.80 m, and one of its angles is 31.0°. What are the lengths of the following sides?

Answers
Answer:
• (a)The length of the side opposite 31.0° is 1.96 meters.
,• (b)The length of the side adjacent 31.0° is 3.26 meters.
Explanation:
In the right triangle:
• The length of the hypotenuse = 3.80 m
,• Let the side ,opposite ,angle 31.0° = x
• Let the side ,adjacent ,angle 31.0° = y
(a)
From trigonometric ratios:
\(\begin{gathered} \sin\theta=\frac{Opposite}{Hypotenuse} \\ \implies\sin31.0\degree=\frac{x}{3.80} \end{gathered}\)Cross multiply:
\(\begin{gathered} x=3.80\times\sin31.0\degree \\ x=1.9571 \\ x\approx1.96\;m \end{gathered}\)The length of the side opposite 31.0° is 1.96 meters.
(b)From trigonometric ratios:
\(\begin{gathered} \cos\theta=\frac{Adjacent}{Hypotenuse} \\ \implies\cos31.0\degree=\frac{y}{3.80} \end{gathered}\)Cross multiply:
\(\begin{gathered} y=3.80\times\cos31.0\degree \\ y=3.2572 \\ y\approx3.26\;m \end{gathered}\)The length of the side adjacent 31.0° is 3.26 meters.
Determine the value of x.
Options:
A) x = 11.2
B) x = 56
C) x = 12.4
D) x = 10

Answers
Answer:
as lengths of tangents of a circle from an external point are equal so
5x+6 = 56
5x = 50
x = 50/5
D) x = 10
Translate the sentence into an equation.
Three less than the product of 2 and a number is equal to 6.
Use the variable x for the unknown number.
Answers
Answer:
2x - 3 = 6
Step-by-step explanation:
solve for 'x':
2x - 3 = 6
2x = 9
x = 9/2 or 4 1/2
Check:
2(9/2) - 3 = 6
9 - 3 = 6
6 = 6
Solve 2x 10 = -4
X = ?
Answers
2x • 10 = -4
20x = -4
x = - 4/20 = -0.2
Answer: x = -0.2