Write an equivalent expression for -5(8-2x)
Answers
Related Questions
The distance between Earth and the Andromeda galaxy is about 2.5 million light years. If one year 365 days, the speed of light in air is 300,000 km/second, then the approximate distance of Earth to the Andromeda galaxy is equal to *A. 2. 500,000 X 365 x 300,000 kmB. 2. 500,000 x 365 X 24 x 300,000 kmc. 2. 500,000 x 365 X 3. 600 x 300,000 kmD. 2. 500,000 x 365 X 24 x 3. 600 x 300,000 km.
Answers
The approximate distance between Earth and the Andromeda galaxy is 2,500,000 x 365 x 24 x 3,600 x 300,000 km.
To calculate the approximate distance between Earth and the Andromeda galaxy, you should use the given distance in light years, the number of days in a year, the speed of light, and the conversion from days to seconds. Here's the step-by-step explanation:
1. You know that the distance is 2.5 million light years or 2,500,000 light years.
2. One year has 365 days.
3. The speed of light is 300,000 km/second.
4. One day has 24 hours, and one hour has 3,600 seconds.
Now, you can calculate the distance:
Distance = (2,500,000 light years) x (365 days/year) x (24 hours/day) x (3,600 seconds/hour) x (300,000 km/second)
This matches option D.
Learn more about Andromeda: https://brainly.com/question/238442
#SPJ11
Please help! I will give Brainliest!
Who is correct?

Answers
Answer:
The inside angles have to equal 180 degrees so
So Hazel is correct
Solve 3[-x + (2 x +1)]=x-1
Answers
The result of the evaluation of the equation given in the task content is; x =-2.
What is the solution of the equation?It follows from the task content that the equation given whose solution is to be determined is;
3[-x + (2 x +1)]=x-1
The equation can be solved as follows;
-3x + 6x +3 = x-1
2x = -4
x = -2
Read more on one variable equation;
https://brainly.com/question/21528555
#SPJ1
O is the centre of this circle.
What is the size of angle x?
Fully justify your answer.

Answers
Answer:
x = 94°
Step-by-step explanation:
ABCD is a cyclic quadrilateral , its 4 vertices lie on the circle.
the opposite angles of a cyclic quadrilateral sum to 180° , that is
x + 86° = 180° ( subtract 86° from both sides )
x = 94°
a tukey multiple comparison is performed to compare the means of 5 populations. how many confidence intervals will be obtained?
Answers
There will be 10 confidence intervals obtained in a Tukey multiple comparison of 5 populations.
In a Tukey multiple comparison, the confidence intervals are constructed to compare the means of all pairs of groups. To calculate the number of confidence intervals, we use the following formula:
C = n(n-1)/2
Where C is the number of confidence intervals, and n is the number of groups. In this case, there are five populations being compared, so n=5. Plugging this into the formula, we get:
C = 5(5-1)/2 = 10
Each confidence interval will provide information about the difference between the means of two groups, with a certain level of confidence. These confidence intervals can be used to identify which pairs of groups have significantly different means.
To learn more about confidence intervals click on,
https://brainly.com/question/28213446
#SPJ4
If you worked 40 hours a week at a minimum wage job in
Oregon, how much would you make in one week before tores
and other deductions?
Answers
Answer:
450+120w
will be the expression
Equation: 450+120w = x
The graph of a linear function f passes through
the point (1,4) and has a slope of -2.
What is the zero of f?
Answers
Answer:
x = -1
Step-by-step explanation:
(x1,y1) = (1,4) and m = 2
(y-y1)/(x-x1) = m
derive the linear function first before finding the zero.
(y-4)/(x-1) = 2
cross multiply
y-4 = 2(x-1)
y-4= 2x - 2
y = 2x - 2+4
y. = 2x + 2 is the linear equation
at y = 0 gives the zero
2x + 2 = 0
2x = -2
x = -2/2
x = -1 is the zero
plzzzzzzzzzzzzzzzzzzzz halppppppppppppppppp

Answers
Answer:
Exact Form:
7/2
Decimal Form:
3.5
Mixed Number Form:
3 (1/2)
I hope this helps! :)
The area of a circle is 18.1 km^2. Find the radius of the circle in kilometers
rounded to the nearest tenth. Use 3.14 for PI, and enter the number only.
Answers
Answer:2.4
Step-by-step explanation:
area = pi* r^2
18.1 /3.14=r^2
5.76 =r^2
Now root square
Answer:
2.4 km
Step-by-step explanation:
πr²=18.1 km²
18.1/3.14=5.76km²
576/100
24/10=2.4km
Re-write the quadratic function below in Standard form
Y= −3(x+1)(x−3)
Answers
Answer:
Y=−3x2+6x+9
Step-by-step explanation:
Kevin recorded the distances he ran last week. The total number of miles he ran on Monday through Wednesday is the same as the total number of miles he ran on Thursday and Friday.
Mon- tues- Wed- thurs- Fri
X X+9 X+4 2x 4x-2
Answers
The distances Kevin ran last week can be represented by the variables X, X+9, X+4, 2X, and 4X-2.
In the summary, the answer states that the distances Kevin ran on Monday through Wednesday (X, X+9, and X+4) are equal to the distances he ran on Thursday and Friday (2X and 4X-2).
To find the solution, we can set up an equation based on the given information:
X + (X+9) + (X+4) = 2X + (4X-2)
By simplifying and solving the equation, we can determine the value of X, which represents the distance Kevin ran on Monday. Once we find the value of X, we can calculate the distances for the remaining days.
For example, if we find that X = 5 miles, then the distances Kevin ran for each day would be:
Monday: 5 miles
Tuesday: 14 miles (5 + 9)
Wednesday: 9 miles (5 + 4)
Thursday: 10 miles (2 * 5)
Friday: 18 miles (4 * 5 - 2)
By solving the equation, we can determine the specific distances Kevin ran on each day of the week.
Learn more about distances here :
https://brainly.com/question/31713805
#SPJ11
f(t)=e5t+4t+7ln(t2+3c)+te-1+5e6
where c is constant
Answers
The function f(t) is defined as e raised to the power 5t plus 4t plus the natural logarithm of the quantity t squared plus 3 times the constant c, raised to the power of 7, plus t times e raised to the power of -1 plus 5 times e raised to the power of 6.
Given a function:
f(t)=e5t+4t+7ln(t2+3c)+te-1+5e6
where c is a constant.
The solution to the question is shown below.
Step 1: We have given a function:
f(t)=e5t+4t+7ln(t2+3c)+te-1+5e6
We have to find the number of words we have to write to express this function in words.
Step 2: Solution
f(t) = et5+4t + ln(t²+3c)⁷ +te-1+5e⁶
Where,
et5+4t = exponential function
ln(t²+3c)⁷ = natural logarithmic function
te-1 = linear function
e⁶ = exponential function
Therefore, f(t) can be expressed in words as:
The function f(t) is defined as e raised to the power 5t plus 4t plus the natural logarithm of the quantity t squared plus 3 times the constant c, raised to the power of 7, plus t times e raised to the power of -1 plus 5 times e raised to the power of 6.
Step 3: Conclusion
Hence, the function f(t) can be expressed in words with:The function f(t) is defined as e raised to the power 5t plus 4t plus the natural logarithm of the quantity t squared plus 3 times the constant c, raised to the power of 7, plus t times e raised to the power of -1 plus 5 times e raised to the power of 6.
To know more about natural logarithm visit:
https://brainly.com/question/29154694
#SPJ11
May someone help please?? I’d give brainliest if I could, it’s not a test btw

Answers
m∠1= 159°
m∠2= 21°
m∠4= 21°
Verification:
(m∠1) + (m∠2) + (m∠3) + (m∠4)
= 159° + 21° + 159° + 21°
= 360° (complete angle)
Hope it helps u!
Answer:
∠3=∠159°
∠2=∠4=180-159=21°
∠1=180-21=159°
mark me brainliest
Consider the functions f(x) = x2 + 2x and g(x) = 4 + x. Step 3 of 4: Find (fog)( - 2).
Answers
The value of (f◦g)(-2) is 8. The composition of the functions f and g at the point x = -2 yields a result of 8.
To find (f◦g)(-2), you first need to evaluate g(-2) and then plug the result into the function f.
Here's the step-by-step process:
1. Evaluate g(-2):
g(-2) = 4 + (-2) = 2
2. Now, plug the result (2) into the function f:
f(2) = (2)^2 + 2(2) = 4 + 4 = 8
Therefore, the value of (f◦g)(-2) is 8. The composition of the functions f and g at the point x = -2 yields a result of 8.
Learn more about composition functions :
https://brainly.com/question/30660139
#SPJ11
I only have 10 minutes left. Thank you for helping!!
Can you prove that r || 8 ? Explain

Answers
Answer:
C
Step-by-step explanation:
The converse angles Theorem states that if two same side interior angles that are cut by a transversal add up to 180, the lines containing thr transversal are parallel.
The transversal cut line r and s but 143+47=190 not 180.
So c fits this description.
Find f(- 2) for \(f(x) = 5 \times {3}^{x} \)
![Find f(- 2) for [tex]f(x) = 5 \times {3}^{x} [/tex]](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/ngDurln2pQjPFGRn7fZ3sef6Qp1vuSI3.png)
Answers
Given:
\(f(x)=5\times3^x\)Find: f(-2)
Explanation:
put x=-2 in the given equation.
\(\begin{gathered} f(x)=5\times3^x \\ x=-2 \\ f(-2)=5\times3^{-2} \\ f(-2)=\frac{5}{3^2} \\ f(-2)=\frac{5}{9} \end{gathered}\)Final answer: the required answer is
\(\frac{5}{9}\)Expand the binomial using the binomial theorem: (3x-4)^5
Can someone explain how you solve this?
Answers
Answer:
Step-by-step explanation:
We worry about 2 things:
-terms power
-coefficient for each term
(3x-4)^5, has 2 terms 3x and -4
-Start with the first term to the highest power 5 and second term to the lowest power 0, then the high power goes down and low power increases until the first term has the lowest power 0 and the second term has the highest power 5.
-The coefficients for each term we take it from the Pascal triangle.
For the the power 5 the coefficients are 1, 5, 10, 10, 5, 1
\((3x-4)^{5} = 1*(3x)^{5} *(-4)^{0} +5*(3x)^{4} *(-4)^{1} +10*(3x)^{3} *(-4)^{2}+10*(3x)^{2} *(-4)^{3}+5*(3x)^{1} *(-4)^{4}+1*(3x)^{0} *(-4)^{5}\)
Simplify:
\((3x-4)^{5} = 3^{5} x^{5} -20*3^{4} x^{4} +160*3^{3} x^{3}-640*3^{2} x^{2}+1280*3x-1024\)
\((3x-4)^{5} = 243 x^{5} -1,620x^{4} +4,320 x^{3}-5,760x^{2}+3,840x-1024\)
from 2005 to 2018, the annual investment in renewable energy sources in the united states increased from $11.4 billion to $46.5 billion. calculate the percent change in renewable energy investment in the us from 2005 to 2018.
Answers
To calculate the percent change in renewable energy investment in the US from 2005 to 2018, you can use the following formula:
Percent change = ((Final value - Initial value) / Initial value) * 100%
In this case, the initial value is $11.4 billion in 2005 and the final value is $46.5 billion in 2018. Plugging these values into the formula, we get:
Percent change = (($46.5 billion - $11.4 billion) / $11.4 billion) * 100%
= ($35.1 billion / $11.4 billion) * 100%
= 3.085 * 100%
= 308.5%
So, the percent change in renewable energy investment in the US from 2005 to 2018 was 308.5%, a substantial increase over the 13-year period.
Use Inverse Laplace Transformation to convert s-domain to time-domain function for the following functions
a)
F(s) = \(\large{\frac{2e^{-0.5s}}{s^2-6s+9}}\)
\(f(t)=\) ....
b)
F(s) = \(\large{\frac{s-1}{s^2-3s+2}}\)
\(f(t)=\) .....
c)
F(s) = \(\large{\frac{s-1}{s^2+s-2}}\)
\(f(t)=\) ....
d)
F(s) = \(\large{\frac{e^{-s}(s-1)}{s^2+s-2}}\)
\(f(t)=\) ....
Answers
The inverse Laplace transform of F(s) is:
\(f(t) = e^(-t)\)
How did we get the value?To find the inverse Laplace transform of each function, we need to express them in terms of known Laplace transforms. Here are the solutions for each function:
a)
\(F(s) = \large{\frac{2e^{-0.5s}}{s^2-6s+9}}\)
To find the inverse Laplace transform, we first need to factor the denominator of F(s). The denominator factors as (s - 3)². Therefore, we can rewrite F(s) as:
\(F(s) = \large{\frac{2e^{-0.5s}}{(s-3)^2}}\)
Now, we know that the Laplace transform of eᵃᵗ is 1/(s - a). Therefore, the inverse Laplace transform of
\(e^(-0.5s) \: is \: e^(0.5t).\)
Applying this, we get:
\(f(t) = 2e^(0.5t) * t \\
b) F(s) = \large{\frac{s-1}{s^2-3s+2}}\)
We can factor the denominator of F(s) as (s - 1)(s - 2). Now, we rewrite F(s) as:
\(F(s) = \large{\frac{s-1}{(s-1)(s-2)}}\)
Simplifying, we have:
\(F(s) = \large{\frac{1}{s-2}}\)
The Laplace transform of 1 is 1/s. Therefore, the inverse Laplace transform of F(s) is:
\(f(t) = e^(2t) \\
c) F(s) = \large{\frac{s-1}{s^2+s-2}}
\)
We factor the denominator of F(s) as (s - 1)(s + 2). The expression becomes:
\(F(s) = \large{\frac{s-1}{(s-1)(s+2)}}\)
Canceling out the (s - 1) terms, we have:
\(F(s) = \large{\frac{1}{s+2}}\)
The Laplace transform of 1 is 1/s. Therefore, the inverse Laplace transform of F(s) is:
\(f(t) = e^(-2t) \\
d) F(s) = \large{\frac{e^{-s}(s-1)}{s^2+s-2}}\)
We can factor the denominator of F(s) as (s - 1)(s + 2). Now, we rewrite F(s) as:
\(F(s) = \large{\frac{e^{-s}(s-1)}{(s-1)(s+2)}}\)
Canceling out the (s - 1) terms, we have:
\(F(s) = \large{\frac{e^{-s}}{s+2}}\)
The Laplace transform of
\(e^(-s) \: is \: 1/(s + 1).\)
Therefore, the inverse Laplace transform of F(s) is:
\(f(t) = e^(-t)\)
learn more about inverse Laplace transform: https://brainly.com/question/27753787
#SPJ4
what does the symmetric bell shape of the normal curve imply about the distribution of individuals in a normal population?
Answers
Answer:
Answer and Explanation: The symmetric bell shape of the normal curve implies that the skewness of the distribution of the data is 0, and most of the observation is located at the middle of the distribution. The shape of the normal distribution is not positive and negative skewed, the shape seems to be bell-shaped.
HOPE THIS HELPS!
Need help with this math question

Answers
Answer:
SAS
Step-by-step explanation:
The sides are equal on the same side
the angles are also equal
and the other sides too
10. Jenn went to the farmer's market with $40. She brought a 10 lb bag of
potatoes for $6, a pie for $8,4 qt frest strawberries for $4 per qt, and 5 lb
of apples at $1. 49 per lb. What percent of the $40 did she still have when
she left? *
Answers
Answer:
Step-by-step explanation:
Find all the expenses:
potatoes: $6
pie: $8.4
strawberry: $4
apples: $1.49 * 5 => $7.45
total=> 6 + 8.4 + 4 + 7.45 = $25.85
Rule:
$40 = 100%
$25.85 = x%
=> x = ($25.85 * 100%) / $40 = 64.625%
hey double check if I added wrong, and if it is repeat the calculation,
hope it helps
Given: AB = CD and BC = AD.
Prove: AB l| CD and BC || AD.
I need the reasons and the statements!!

Answers
Step-by-step explanation:
AC = AC by reflexive
∆ABC = ∆CDA by SSS
Angle CAD = angle ACB by CPCTC
Since alt interior angles are congruent, BC //AD
Repeat the same process to show AB//CD
hello! please help me solve this asap!
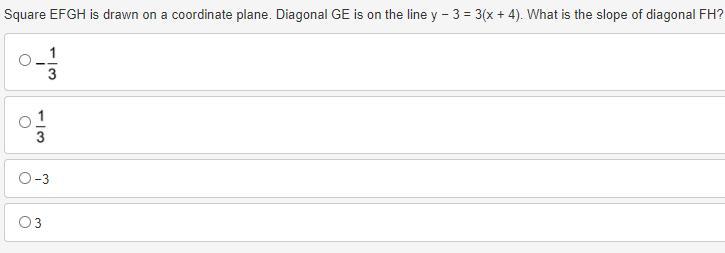
Answers
Answer:
3
Step-by-step explanation:
y-3 = 3x+12
y = 3x +15
so slope = 3 ( number next to the x)
16×25×15 =?
4+11÷2=?
?-?=?
Answers
Answer:
16x25x15=6000
4+11÷2=9.5
Step-by-step explanation:
1) 16x25x15 is 16 times 25 times 15, which is 6000
2) This question requires BIDMAS/BODMAS. As you start with the multiplication (Brackets Indices Multi Divide Add Subtract) 11÷2 = 5.5, 5.5+4=9.5
At sunset, the temperature was -6.4. The temperature then rose 16.9 by noon and then decreased by 12.7 by midnight. What was the temperature at midnight?
Answers
-2.2º
1) Given that at sunset it was -6.4, then ir rose 16.9 by noon
2) Then it decreased by 12.7, so
10.5 -12.7 =-2.2 The sign of the greatest number in absolute value prevails
3) Hence, at midnight the Temperature was -2.2

If A and B are mutually exclusive events with P(A) = 0.4 and P(B) = 0.5, then P(A ∩ B) =
a. 0.10
b. 0.90
c. 0.00
d. 0.20
Answers
The probability of A and B occurring simultaneously (P(A ∩ B)) is c. 0.00.
In this scenario, A and B are stated to be mutually exclusive events. Mutually exclusive events are events that cannot occur at the same time. This means that if event A happens, event B cannot happen, and vice versa.
Given that P(A) = 0.4 and P(B) = 0.5, we can deduce that the probability of A occurring is 0.4 and the probability of B occurring is 0.5. Since A and B are mutually exclusive, their intersection (A ∩ B) would be an empty set, meaning no outcomes can be shared between the two events. Therefore, the probability of A and B occurring simultaneously, P(A ∩ B), would be 0.
To further clarify, let's consider an example: Suppose event A represents flipping a coin and getting heads, and event B represents flipping the same coin and getting tails. Since getting heads and getting tails are mutually exclusive outcomes, the intersection of events A and B would be empty. Therefore, the probability of getting both heads and tails in the same coin flip is 0.
In this case, since events A and B are mutually exclusive, the probability of their intersection, P(A ∩ B), is 0.
Therefore, the correct answer is: c. 0.00
Learn more about Probability
brainly.com/question/795909
#SPJ11
In Exercises 1-4, find the exact values of the six trigono-
metric functions of the angle shown in the figure. (Use the
Pythagorean Theorem to find the third side of the triangle.)
1.
2.
0
8
6
0
13
5
Only number 1 and 2

Answers
Answer:
1. 10
2. 12
Step-by-step explanation:
1. 8² + 6² = y² (Taking the unknown side as y)
64 + 36 = 100
y² = 100
y = 10
2. 5² + x² = 13² (Taking the unknown side as x)
x² = 13² - 5²
= 169 - 25
= 144
x² = 144
x = 12
x^2+y^2−4x+2y=b
The radius of the circle is 7 units. What is the value of b in the equation?
Answers
Answer:
b = 44
Step-by-step explanation:
We can complete the square(s) to put the equation in standard form. Then we can find the value of b that makes the radius be 7 units.
__
x^2 +y^2 -4x +2y = b . . . . . given
(x^2 -4x) +(y^2 +2y) = b . . . . group by variable
(x^2 -4x +4) +(y^2 +2y +1) = b + 4 + 1 . . . . complete the squares
(x -2)^2 +(y +1)^2 = b +5 = 7^2 = 49 . . . . . write as squares, show radius
b = 49 -5 = 44 . . . . subtract 5
The value of b to make the radius 7 is 44.
_____
The standard form of the equation for a circle is ...
(x -h)^2 +(y -k)^2 = r^2 . . . . . center (h, k), radius r
A card is drawn one at a time from a
well-shuffled deck of 52 cards. In 13
repetitions of this experiment, 1
king is drawn. If E is the event in
which a king is drawn, find the
experimental probability P(E).
P(E)=

Answers
The empirical probability of drawing the cards will be 6 / 55.
What is empirical probability?The ratio of the number of outcomes in which a defined event occurs to the total number of trials, not in a theoretical sample space but in a real experiment, is the empirical probability, relative frequency, or experimental probability of an event.
Given that a card is drawn one at a time from a well-shuffled deck of 52 cards. In 13 repetitions of this experiment, 1 king is drawn.
The number of kings in a well-shuffled deck consists of 52 cards which is 4.
The number of ways of drawing consists of 4 kings in 13 repetitions which is ¹³C₄.
In 13 repetitions, 2 kings are drawn by ¹³C₂ ways,
The empirical probability will be calculated as,
P(E) = ¹³C₂ / ¹³C₄
P(E) = [ (13!) / (13-2)! ] ÷ [ (13!) / ( 13-4)!(4!) ]
P(E) = ( 4 x 3 ) / ( 11 x 10)
P(E) = 6 / 55
To know more about empirical probability follow
https://brainly.com/question/16972278
#SPJ1