Write a rational expression that is equal to the following rational expression when x does not equal 1 or -5

4(x-1)/(x-1)(x+5)

will give brainliest pls answer quick and good

The matrix M is: M = [2/9 -8/27 , 4/9 -8/27 ]

Let's say that M is a 2 x 2 matrix that satisfies M × [3 -2 , 6 -8 ] = [-2 16]. This means that the product of matrix M and matrix [3 -2 , 6 -8 ] will give us the result matrix [-2 16].  We know that the product of two matrices is equal to the sum of the products of their corresponding elements.  We can use this knowledge to solve for the unknown elements in matrix M. Let us assume that M = [a b , c d] so that we can solve for its elements.

a(3) + b(6) = -2 ... (1) c(3) + d(6) = 16 ... (2) a(-2) + b(-8) = -2 ... (3) c(-2) + d(-8) = 16 ...

(4)Simplifying equations (1) to (4),  we get:

3a + 6b = -2 ... (5) 3c + 6d = 16 ... (6) -2a - 8b = -2 ... (7) -2c - 8d = 16 ... (8)

Solving for a, b, c, and d, we get:a = 2/9 b = -8/27 c = 4/9 d = -8/27.

for such more questions on matrix

https://brainly.com/question/1279486

#SPJ8

Answer:

The first and third choices

\(y = \dfrac{3}{2}x + 3\)

and

\(2y-3x=6\)

Step-by-step explanation:

(I cannot properly see the leading negative signs in choices 4 and 5, I copied/pasted your question choices from Brainly post and zoomed)

First understand what x and y intercepts are

The y-intercept is the value of y where the graph of the equation crosses the y-axis, It is the value of y when x = 0

The x-intercept is the value of x where the graph of the equation crosses the x-axis, It is the value of x when y = 0

We are given that the x-intercept is (-2, 0) and y = (0,3)

We can use a process of elimination to get rid of obviously incorrect choices and then work on the possible correct ones depending on whether we come up with the correct values of y first and eliminating those that do not match x =0, y =3 or (0,3) and then see if the x-intercept is (-2,0)

Answer:

Total=4 +3=7

For the 4

4÷7×70=£40

For the 3

3÷7×70=£30

So the division of £70 in ratio 4:3 is £40:£30

well, the table has 5 points in it, let's pick any two hmmm say let's  use hmmm (2 , 7) and (6 , 17)

\((\stackrel{x_1}{2}~,~\stackrel{y_1}{7})\qquad (\stackrel{x_2}{6}~,~\stackrel{y_2}{17}) ~\hfill \stackrel{slope}{m}\implies \cfrac{\stackrel{rise} {\stackrel{y_2}{17}-\stackrel{y1}{7}}}{\underset{run} {\underset{x_2}{6}-\underset{x_1}{2}}}\implies \cfrac{10}{4}\implies \cfrac{5}{2}\)

when x = 0, from the table, y = 2, so there's the y-intercept.

The sequence of natural numbers that leaves a remainder of 3 when divided by 10 is:

3, 13, 23, 33, 43, 53, 63, 73, 83, 93, 103, 113, ...

\(\huge{\mathfrak{\colorbox{black}{\textcolor{lime}{I\:hope\:this\:helps\:!\:\:}}}}\)

♥️ \(\large{\underline{\textcolor{red}{\mathcal{SUMIT\:\:ROY\:\:(:\:\:}}}}\)

Answer:10

Step-by-step explanation:

found area

Answer:

the answer is 32,768 hopes this helps

Step-by-step explanation:

8^5 = 8x8x8x8x8 = 64x8x8x8= 64x64x8 = 4096x8= 32,768

Answer:

=y + 3 = -6(x +9)

Step-by-step explanation:

hope that will help you

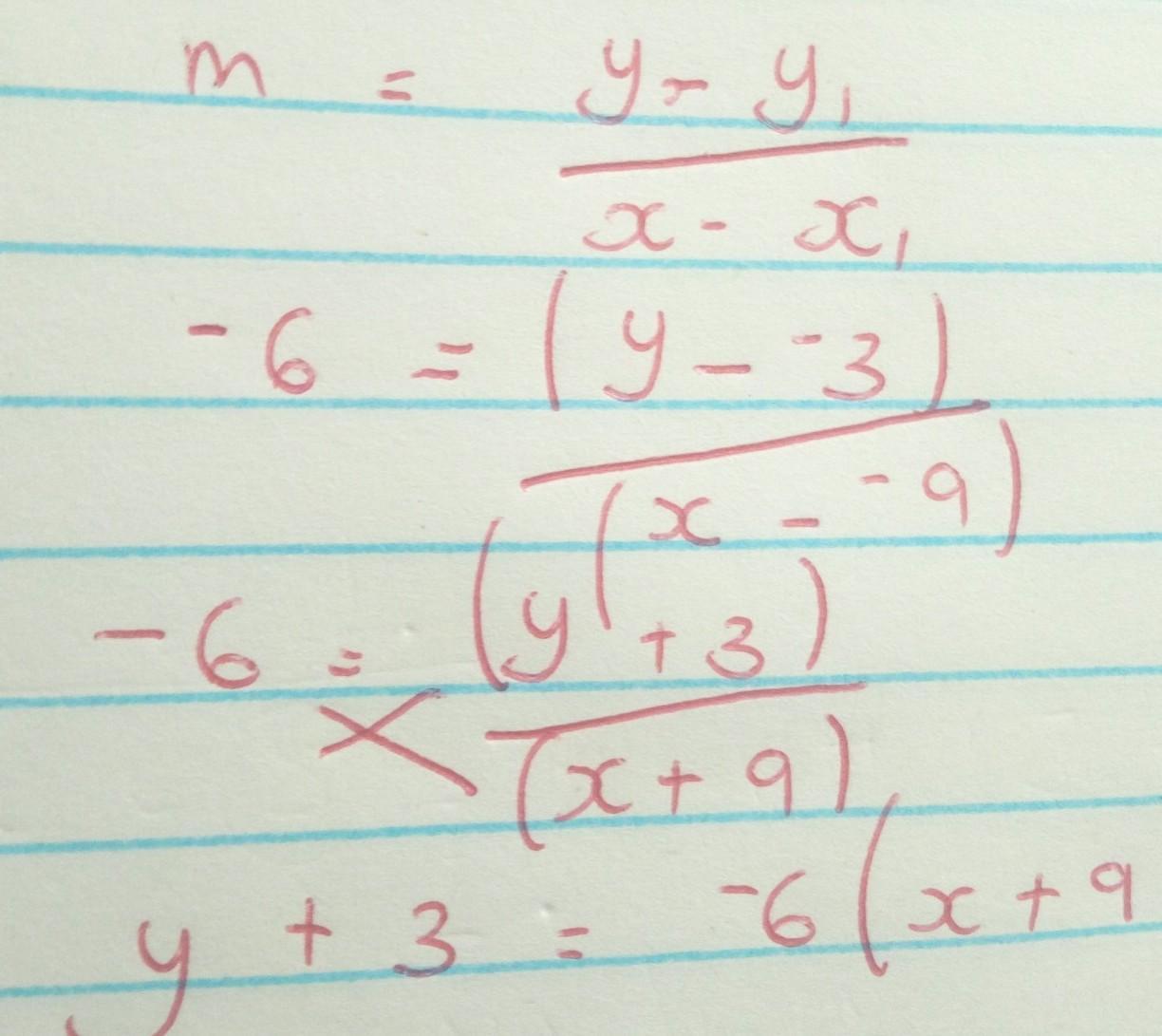
Answer:

D

Step-by-step explanation:

............................................9

The price of the Motorcycle, not including the tax, is $11,500

The price of the motorcycle before the tax, we need to subtract the tax amount from the total price, including the tax. Let's denote the price of the motorcycle before tax as P.

Given:

Tax rate = 12.5%

Tax amount = $1437.50

We know that the tax amount is equal to 12.5% of the price of the motorcycle:

Tax amount = 0.125 * P

We can set up the equation and solve for P:

0.125 * P = $1437.50

To isolate P, divide both sides of the equation by 0.125:

P = $1437.50 / 0.125

Performing the calculation:

P = $11,500

Therefore, the price of the motorcycle, not including the tax, is $11,500.

Tax amount = 0.125 * $11,500 = $1437.50

The tax amount matches the given information, confirming that the price of the motorcycle before tax is indeed $11,500.

To know more about Motorcycle.

https://brainly.com/question/29915026

#SPJ11

The length of the base of the triangle is 3/2 meters.

To find the length of the base of the triangle, we can use the formula for the area of a triangle, which is given by the formula:

Area = (1/2) * base * height.

We are given that the area of the triangle is 3/10 square meters, and the height is 2/5 meters. Let's denote the length of the base as b.

Plugging in the given values into the formula, we have:

(1/2) * b * (2/5) = 3/10.

To solve for b, we can simplify the equation:

b * (2/5) = (3/10) * 2.

Multiplying both sides of the equation by 5/2 to isolate b, we get:

b = (3/10) * 2 * (5/2).

Simplifying further, we have:

b = (3/10) * 5 = 15/10 = 3/2.

In summary, using the formula for the area of a triangle and the given values, we find that the length of the base of the triangle is 3/2 meters.

For more such question on triangle. visit :

https://brainly.com/question/17335144

#SPJ8

Answer:

4.) 12

Step-by-step explanation:

\( \frac{2}{3} (9a + 18b) = 6a + kb \\ \\ \implies \: \frac{2}{3} \times 9a + \frac{2}{3} \times 18b = 6a + kb \\ \\ \implies \: { 6a} + 12b = 6a + kb \\ \\ \implies \: \cancel{ 6a} + 12b - \cancel{ 6a} = kb \\ \\ \implies \: 12b = kb \\ \\ \implies \: k = \frac{12\cancel b}{\cancel b} \\ \\ \huge \implies \: k = 12\)

Answer:

5+x=50-10

Step-by-step explanation:

Answer:

Kaylaa   do you use  desmos graphing calculator?  it's an online graphsing tool and would make this very easy for you. Maybe you are not allowed to use a calculator?

Step-by-step explanation:

with out  a calculator it's a long math process,  1st because each of the equations are equal to  Y,  we can set each of them equal to each other. like this

\(\sqrt{x-8}\) + 3  =  - \((x-5)^{2}\) + 18

\(\sqrt{x-8}\)     =  - \((x-5)^{2}\)  +18 -3

\(\sqrt{x-8}\)   =    - \((x-5)^{2}\)  + 15

\(\sqrt{x-8}\)   = -[ (x-5)*(x-5) ] + 15

\(\sqrt{x-8}\)  = -[ \(x^{2}\) - 10x + 25] +15

\(\sqrt{x-8}\)  = -\(x^{2}\) + 10x -25 +15

 \(\sqrt{x-8}\) = -\(x^{2}\) + 10x -10

-  \(\sqrt{x-8}\)  = \(x^{2}\) - 10x +10

(-  \(\sqrt{x-8}\))^2  = (  \(x^{2}\)- 10x +10)^2

this turns into a 4 order polynomial.   I used a solver to find x

x = 8.75884....  approx

so the question asks what is the point at the nearest 1000th,  which is 8.759  

then they ask what is the point at the nearest 100th, which is  

8.76

I'm attaching the graph, if it helps  :P

Answer:

x3=4=2

Step-by-step explanation:

Add like terms. I believe that's what you're going for...

Hope this helped :)

Answer:

A pencil is about 19 centimeters long

Answer:

if 100 inches=254 centimeters

then 10 inches=x

100x=2540

x=2540/100

x=25.4 centimeters

Given a Math exam with 7 short answer questions and Peter intending to answer three of them, there are a total of 35 different combinations of short answer questions he can choose.

To determine the number of combinations, we can use the concept of combinations in combinatorics. The formula for combinations is given by:

C(n, r) = n! / (r! * (n - r)!)

Where:

C(n, r) represents the number of combinations of choosing r items from a set of n items.

n! denotes the factorial of n, which is the product of all positive integers up to n.

In this case, Peter wants to answer three out of the seven questions, so we can calculate it as:

C(7, 3) = 7! / (3! * (7 - 3)!) = 7! / (3! * 4!)

Simplifying further:

7! = 7 * 6 * 5 * 4 * 3 * 2 * 1

3! = 3 * 2 * 1

4! = 4 * 3 * 2 * 1

C(7, 3) = (7 * 6 * 5 * 4 * 3 * 2 * 1) / [(3 * 2 * 1) * (4 * 3 * 2 * 1)]

After canceling out common terms, we get:

C(7, 3) = 7 * 6 * 5 / (3 * 2 * 1) = 35

Therefore, there are 35 different combinations of short answer questions Peter can choose to answer.

Learn more about combinations in combinatorics here: brainly.com/question/13261685

#SPJ11

This method is effective because it breaks down the percentage into smaller parts that are easier to calculate mentally. By finding 5% and 1% separately and then adding them together, you can quickly find the percentage that you need.To find 7% of $1000, there are various mental math methods that one can use. One of the best methods is to use a combination of the 5% and 1% methods. Here's how to do it:

Step 1: Find 5% of $1000
5% of $1000 is $50

Step 2: Find 1% of $1000
1% of $1000 is $10

Step 3: Add the two values together
$50 + $10 = $60

Step 4: Find 1% of $60
1% of $60 is $0.60

Step 5: Multiply $0.60 by 7 to get the final answer
$0.60 x 7 = $4.20

Therefore, 7% of $1000 is $4.20.

This method is effective because it breaks down the percentage into smaller parts that are easier to calculate mentally. By finding 5% and 1% separately and then adding them together, you can quickly find the percentage that you need.

For more question on percentage

https://brainly.com/question/24877689

#SPJ8

Answer:

Yes

Step-by-step explanation:

Yes, because 6.9 > 0.95

Answer:

Yes

Step-by-step explanation:

Yes....about 7 times faster because   6.9 >> .95 meters

The correct formula to simulate a variable uniformly distributed between 100 and 200 using x is c. 100 + 100x.

To simulate a variable uniformly distributed between 100 and 200 using a random number x between 0 and 1, you can use the formula:

Variable = 100 + (200 - 100) * x

Let's break down the formula:

a. 100 + x: This will give a variable that ranges from 100 to 101, not between 100 and 200.

b. 200 - x: This will give a variable that ranges from 199 to 200, not between 100 and 200.

c. 100 + 100x: This formula is correct and will give a variable that ranges from 100 to 200, with x ranging from 0 to 1.

d. 200x: This formula will give a variable that ranges from 0 to 200, not between 100 and 200.

Therefore, the correct formula to simulate a variable uniformly distributed between 100 and 200 using x is c. 100 + 100x.

To learn more about variable

https://brainly.com/question/82796

#SPJ11

The minimum wage set by the government at $7.50 per hour does not result in a pay cut for unskilled workers, as it is below the equilibrium wage of $8.00 per hour.

The wage rate remains unchanged, and the labor market remains in balance.

The statement is false.

False.

The equilibrium wage in the market for unskilled labor is $8.00 per hour, which means that the market naturally sets the wage rate at this level, based on the forces of supply and demand.

The government then sets a minimum wage at $7.50 per hour.

Since the minimum wage is below the equilibrium wage, it does not directly impact the wage rate for unskilled workers.
The equilibrium wage represents the point at which the supply of labor (the number of workers willing to work at a given wage) equals the demand for labor (the number of workers that employers are willing to hire at a given wage).

In this case, both workers and employers are satisfied with the $8.00 per hour wage, and the labor market is balanced.
The government sets a minimum wage below the equilibrium wage, it essentially sets a wage floor that is not binding. Employers are still willing to pay the equilibrium wage of $8.00 per hour, and workers are still willing to accept this wage.

The wage for unskilled workers remains at $8.00 per hour, and there is no pay cut of 50 cents per hour.

For similar questions on Wages

https://brainly.com/question/29251394

#SPJ11

The ponderal index cannot be computed without the value of the constant "a" in the formula. Therefore, the ponderal index for a person who is 76 inches tall and weighs 192 pounds cannot be determined.

To compute the ponderal index, we need the formula and the value of the constant "a."

a) The formula for the ponderal index is given as I = a, where I represents the ponderal index and a is a constant. However, the value of the constant "a" is missing in the provided information. Without knowing the value of "a," we cannot compute the ponderal index for a person who is 76 inches tall and weighs 192 pounds.

b) Similarly, without knowing the value of the constant "a," we cannot determine the weight of a man who is 77 inches tall and has a ponderal index of 11.56.

To compute the ponderal index or determine the weight, we need the specific value of the constant "a" in the given formula.

Learn more about index here :-

https://brainly.com/question/32793068

#SPJ11

Answer:

Step-by-step explanation:

we have\(\left \{ {{y=x+14} \atop {x+2y=36}} \right.\)

⇒\(\left \{ {{x=y-14} \atop {x=-2y+36}} \right.\)

⇒y-14 = -2y+36

⇒3y = 50

⇒y = \(\frac{50}{3}\)

⇒x = y-14 = \(\frac{8}{3}\)

Answer:

\(\tt \bigg(\dfrac{8}{3}, \: \dfrac{50}{3}\bigg)\)

Step-by-step explanation:

Given equations are,

\({\implies \sf y = x+14 \qquad - \big\lgroup eq^n \:1 \big\rgroup}\)

\({\implies\sf x+2y=36 \qquad - \big\lgroup eq^n \:2 \big\rgroup}\)

We have the value of y as x + 14. Let us substitute the value of y in eqⁿ 1. Then we get,

\({\implies \sf x + 2(x+14) = 36}\)

\({\implies \sf x + 2x+28 = 36}\)

\({\implies \sf 3x+28 = 36}\)

\({\implies \sf 3x+28-28 = 36-28}\)

\({\implies \sf 3x = 8}\)

\({\implies \boxed{\sf x= \dfrac{8}{3}}}\)

Now, put the value of x in eqⁿ 1.

\({\implies \sf y = x+14}\)

\({\implies \sf y = \dfrac{8}{3}+14}\)

\({\implies \sf y = \dfrac{8}{3}+\dfrac{14}{1}}\)

\({\implies \sf y = \dfrac{8}{3}+\dfrac{14\times 3}{1\times 3}}\)

\({\implies \sf y = \dfrac{8}{3}+\dfrac{42}{3}}\)

\({\implies \sf y = \dfrac{8+42}{3}}\)

\({\implies \boxed{\sf y = \dfrac{50}{3}}}\)

Therefore,

\(\sf \bigg(\dfrac{8}{3} , \dfrac{50}{3} \bigg) \:is \:the \:solution \:for \:the\:given \:equation.\)

The Solution using two methods are 323, .291, the correct option is B`.

Probability of an event is a measurement of how likely an event can occur as an outcome of a random experiment.

Probability ranges from 0 to 1, both inclusive. Events whose probability is closer to 0 are rarer to occur than those whose probabilities are closer to 1 (relatively).

When converted to percentage, we just need to multiply its decimal representation by 100. In percentage form, the probability ranges from 0% to 100%.

Given;

Frank is a champion fish charmer who can charm fish with .62 probability of success

He attempts to charm 100 fish, what's the probability he'll charm

between 60 and 80 inclusive

Now, probability out of 100

=62

This is between 60 and 80

So, 323

Therefore, the probability will be 323 and .291

Learn more about interpretation of probability here:

https://brainly.com/question/23024246

#SPJ1

There are 1234 t shirts that need to be shipped. To ship 1234 t-shirts, a total of 39 boxes are required, as each box can hold 32 t-shirts.

To calculate the number of boxes required to ship 1234 t-shirts, we need to divide the total number of t-shirts by the number of t-shirts that can fit in one box. In this case, as each box can fit 32 t-shirts, we need to divide 1234 by 32.

Using long division, we can find that 32 goes into 1234, 38 times with a remainder of 10. However, we still have 10 t-shirts that need to be shipped, which means we need an additional box to fit them. Therefore, the total number of boxes needed to ship 1234 t-shirts is 39 (38 boxes to fit 1216 t-shirts and 1 additional box to fit the remaining 10 t-shirts).

It's always important to ensure that all the items fit comfortably in the boxes without any damage or risk of items falling out. In this case, we can also use this information to plan and optimize the shipping process by arranging the boxes according to the available storage and transportation capacity.

To learn more about long division click here, brainly.com/question/28824872

#SPJ11

1) (a) The transformations that occur from the parent function are horizontal translation of 2 units to the left and vertical translation of 4 units to the down.

(b) (-2, -4)

(c) Graph is given below.

1) Given a function,

g(x) = (x + 2)² - 4

(a) Given a parent function p(x) = x².

We can write g(x) as,

g(x) = p(x + 2) - 4

So the transformation is horizontal translation of 2 units to the left and vertical translation of 4 units to the down.

(b) Vertex formula of a parabola is,

y = a (x - h)² + k, where (h, k) is the vertex.

Comparing the given function with vertex form,

Vertex of the parabola = (-2, -4)

(c) Graph of g(x) will be a parabola with vertex at (-2, -4).

It is given below.

Learn more about Transformations here :

https://brainly.com/question/23186655

#SPJ1

(a) The possible rational roots of the polynomial f(x) = x³ + 5x² - 17x + 21 are ±1, ±3, ±7, and ±21. (b) Given that 1 is a root, the polynomial can be factored as f(x) = (x - 1)(x² + 6x - 21). (c) The inequality f(x) ≥ 0 is satisfied for x ≤ -3 or -1 ≤ x ≤ 1 in interval notation.

(a) To find the possible rational roots, we can use the Rational Root Theorem. The possible rational roots are given by the factors of the constant term (21) divided by the factors of the leading coefficient (1). So, the possible rational roots are ±1, ±3, ±7, and ±21.

(b) Given that 1 is a root, we can use synthetic division to divide f(x) by (x - 1) to obtain the quotient x² + 6x - 21. Therefore, f(x) = (x - 1)(x² + 6x - 21).

(c) To find when f(x) ≥ 0, we need to determine the intervals where the function is positive or zero. From the factored form, we can see that the quadratic factor x² + 6x - 21 is positive for x ≤ -3 and x ≥ 1. The linear factor (x - 1) changes sign at x = 1. Therefore, f(x) ≥ 0 when x ≤ -3 or -1 ≤ x ≤ 1.

In interval notation, the solution is (-∞, -3] ∪ [-1, 1].

Learn more about inequality here:

https://brainly.com/question/20383699

#SPJ11

Consider the following polynomial: f(x) = x³5x² - 17x + 21 (a) List all possible rational roots. (Do not determine which ones are actual roots.) (b) Using the fact that 1 is a root, factor the polynomial completely. (C) When is f(x) ≥ 0? Express your answer in interval notation.  

Answer: The value of b is 22.62

Step-by-step explanation: 20 is the opposite of b, 52 is the hypotenuse. Because we're given the opposite and hypotenuse, we have to use sine. So....

sin b=20/52

sin b = 0.38461538461

then using inverse of sine, the equation would be sin^-1(0.38461538461)

by putting that into the calculator you get 22.61986495 (aka 22.62)

Based on the triangle inequality theorem, if fd = 20 units and de = 52 units, the value of b is approximately 71 units.

To find the value of b, we can use the triangle inequality theorem. According to this theorem, the sum of the lengths of any two sides of a triangle must be greater than the length of the remaining side.

In this case, we have fd = 20 units and de = 52 units. Let's assume that b is the length of the remaining side.

Using the triangle inequality theorem, we can write the following inequality:

fd + de > b

Substituting the given values, we get:

20 + 52 > b

72 > b

Therefore, the value of b must be less than 72 units.

To round the solution to the nearest hundredth, we can round down to the nearest whole number, which is 71.

So, the value of b is approximately 71 units.

In conclusion, based on the triangle inequality theorem, if fd = 20 units and de = 52 units, the value of b is approximately 71 units.

Learn more about triangle inequality theorem from the given link:

https://brainly.com/question/30956177

#SPJ11

Answer:

-61

Step-by-step explanation:

We use the distributive property to distribute 6 to both x and 11. This gives 6x+66=-300. Subtracting both sides by 66 gives 6x=-366. Dividing both sides gives x=-61.