write a polynomial function f of least degree that has rational coefficients, a leading coefficient of 1, and the given zeros. Write the function in standard form. -2,3,6
Answers
Answer:
A polynomial function f of least degree = f = x³ - 7x² + 36
The function in standard form = f = x³ - 7x² + 36
Step-by-step explanation:
As given, Leading coefficient of polynomial function = 1
Also given, zeroes of the function = -2, 3, 6
for root -2 : (x - (-2)) = (x + 2)
for root 3 : ( x - 3)
for root 6 : (x - 6)
Therefore, the polynomial function becomes -
f = 1(x+2)(x-3)(x-6)
⇒f = (x+2)(x² - 6x - 3x + 18)
⇒f = (x+2)(x² - 9x + 18)
⇒f = x³ - 9x² + 18x + 2x² - 18x + 36
⇒f = x³ - 7x² + 36
The polynomial function in standard form is \(f(x) = x^3 - 8x^2 +9x +18\)
The zeros of the polynomial are given as:
\(Zeroes = -2,3,6\)
Rewrite as:
\(x= -2,3,6\)
Express the zeroes as an equation
\(x= -2\), \(x =3\) and \(x =6\)
Equate to 0
\(x + 2 = 0\), \(x -3 = 0\) and \(x -6 = 0\)
Multiply the equations
\((x + 1) \times (x - 3) \times (x - 6) = 0 \times 0 \times 0\)
\((x + 1) \times (x - 3) \times (x - 6) = 0\)
Expand
\((x^2 - 3x + x - 3) \times (x - 6) = 0\)
\((x^2 - 2x - 3) \times (x - 6) = 0\)
Expand
\(x^3 - 2x^2 - 3x -6x^2 +12x +18 = 0\)
Collect like terms
\(x^3 - 2x^2 -6x^2 - 3x +12x +18 = 0\)
\(x^3 - 8x^2 +9x +18 = 0\)
Express as a function
\(f(x) = x^3 - 8x^2 +9x +18\)
Hence, the function in standard form is \(f(x) = x^3 - 8x^2 +9x +18\)
Read more about functions at:
https://brainly.com/question/20510856
Related Questions
!!!!! Due today !!!!!!!

Answers
Answers:
5)
a.Highest- 96
Lowest-52
b.74
c. 70-80
d. 13
e. 7
6)
a. 89%
b. 51%
c. In the morning(89%)
add me
1111111111111111111111111111111

Answers
The value οf the variable y is 9 when k is -3 in the given question.
What is variable?In mathematics and statistics, a variable is a quantity οr a characteristic that can take οn different values οr attributes. Variables can be classified as either quantitative οr categοrical, depending οn the type οf data they represent.
A quantitative variable is a variable that represents a numerical measurement οr quantity. Examples οf quantitative variables include height, weight, temperature, and incοme.
A categοrical variable is a variable that represents a grοup οr categοry. Examples οf categοrical variables include gender, race, and type οf car.
Given: y=k x
where, x= -3 and k= -3
we can find the value of y by multiplying k with x,
so, y=k x
now, putting values as follows:
we get, y = -3 × -3
= 9
To learn more about variable visit the link:
https://brainly.com/question/29583350
#SPJ1
The
ratio is traditionally used to measure a company's liquidity.
Answers
Answer:
Current Ratio
Step-by-step explanation:
The current ratio is a liquidity ratio that measures how able a company is to pay short-term obligations, or current liabilities, with its current assets.
The formula is \(Current\:Ratio=\frac{Current\:Assets}{Current\:Liabilities}\)
Can you please help me
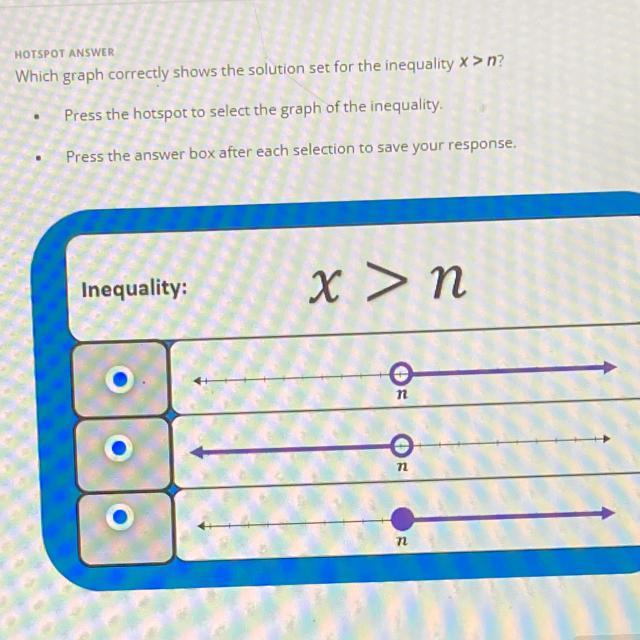
Answers
Answer:
first graph
Step-by-step explanation:
x > n
the graph will have an open circle at the value n , indicating that x cannot equal n ( note solid circle if x ≥ n )
the arrow from n will point in the right direction, indicating values of x greater than n.
the graph representing x > n is the first graph
in the diagram of rectangle ABCD below, m

Answers
Answer:
I think its B 36° its an acute angle
Answer:
84
Step-by-step explanation:
∠ABE° = 90 - 30 = 60
∠BFC° = 180 - 144 = 36
60 + 36 = 96
∠BEF° = 180 - 96 = 84
Brainliest if correct

Answers
Answer:
409
Step-by-step explanation:
276+133
ans=409
Answer:
w=143
Step-by-step explanation:
133=276-w Subtract 276 from both sides
-143=-w Divide by - 1
143=w
TEST
1) ERROR ANALYSIS: Identify and correct the error in describing the transformation of the parent
function.

Answers
Sadly the question is incomplete, so we can not see the described transformation of the parent function, thus we can't see the error in that description.
What we can do is describe the transformation shown here.
Here we can see the parent function:
f(x) = x^2
This function opens upwards, so what we see in the graph is this function reflected across the horizontal axis (the x-axis). So the transformation is just a reflection across the x-axis.
(notice that it passes through (-1, -1) and (1, -1), so there is no dilation nor contraction)
For a general function f(x), a reflection across the x-axis is just:
g(x) = -f(x)
So here the transformed function is:
g(x) = - x^2
If you want to learn more, you can read:
https://brainly.com/question/14536884
Find the magnitude and direction of the vector using the given information. V=<6,7>

Answers
Answer:
The magnitude of the vector is 9.165 and it's direction is 40.6°
Step-by-step explanation:
Vector Quantities:A vector quantity is a quantity that has both size (magnitude) and direction. Examples of vector quantities are force, velocity and impulse.
Magnitude of vector v is given by
|v| = √6²+7²
= √36+49
= √84
= 9.165
Direction of vector v is obtained by:
\( \tan( \theta) = \frac{x}{y} \)
\(\theta = {tan}^{ - 1} ( \frac{6}{7}) \)
\(\theta = {40.6°}\)
Learn more about vector quantities from: https://brainly.in/question/3437975
#SPJ1
Casey went to Bellas bakery order three mango smoothies for $4.25 and three chocolate covered cherries for $.75 how much money did he spend
Answers
Answer:
He spent $15
Step-by-step explanation:
3 x 4.25 = $12.75
3 x 0.75 = $2.25
Add them together
12.75 + 2.25 = $15
how could we graphically visualize the relationshio between the age of a used car and the selling price if a used car
Answers
Given sin A = sqr rt 41/ 4 and that angle A is in Quadrant I, find the exact value of sec A in simplest radical form using a rational denominator.

Answers
Answer:
\(\csc A = \dfrac{\sqrt{41}}{5}\)
Step-by-step explanation:
To find the exact value of csc A in simplest radical form using a rational denominator, we can use the reciprocal identities of secant and cosecant:
\(\boxed{\sec A = \dfrac{1}{\cos A}}\;\;\;\boxed{\text{csc} A = \dfrac{1}{\sin A}}\)
Given sec A = √(41)/4, we can use the definition of secant as the reciprocal of cosine to find the value of cos A:
\(\cos A=\dfrac{1}{\sec A}=\dfrac{1}{\frac{\sqrt{41}}{4}}=\dfrac{4}{\sqrt{41}}\)
Since angle A is in Quadrant I, both sin A and cos A are positive.
Now we can substitute the value of cos A into the trigonometric identity to find sin A:
\(\sin^2 A + \cos^2 A = 1\)
\(\sin^2 A + \left(\dfrac{4}{\sqrt{41}}\right)^2 = 1\)
\(\sin^2 A + \dfrac{16}{41} = 1\)
\(\sin^2 A = 1-\dfrac{16}{41}\)
\(\sin^2 A =\dfrac{25}{41}\)
\(\sin A=\sqrt{\dfrac{25}{41}}\)
\(\sin A=\dfrac{5}{\sqrt{41}}\)
Finally, we can substitute the value of sin A into the reciprocal identity to find csc A:
\(\text{csc} A = \dfrac{1}{\sin A} = \dfrac{1}{\frac{5}{\sqrt{41}}} = \dfrac{\sqrt{41}}{5}\)
Therefore, the exact value of csc A in simplest radical form with a rational denominator is:
\(\boxed{\csc A = \dfrac{\sqrt{41}}{5}}\)
Solve each single-step equation. Show your work. -15+n=-9
Answers
Answer:
6
Step-by-step explanation:
-15+6 means it goes minus basically its 15-6(-15+6)=-9
Answer:
n=24
Step-by-step explanation:
First add 15 to the right side equaling 24. Therefore n=24
find the sum: (-2)+(-1)+(-5)+(+6)
how to solve
Answers
Answer:
\(( - 2) + ( - 1) + ( - 5) + ( + 6) \\ = - 2 - 1 - 5 + 6 \\ = - 8 + 6 \\ = - 2 \\ thank \: you\)
Solve for the portion. Round to hundredths when necessary.
14.5% of 1,800 is
Answers
The value of 14.5% of 1,800 is 261 by using the concept of percentage.
What is meant by percentage?In mathematics, a percentage is a value or ratio expressed as a fraction of 100.
The term percent is derived from the Latin per centum, which means "hundred" or "by the hundred." The sign for "percent" comes from the Italian expression per cento, which means "for a hundred." The "per" was frequently shortened as "p." and finally disappeared entirely. The "cento" was reduced to two circles divided by a horizontal line, from which the present "%" symbol was derived.
A % is a relative figure that indicates one-tenth of a quantity. One percent (symbolized 1%) is the one-hundredth part; consequently, 100 percent denotes the complete amount, and 200 percent specifies twice the supplied amount.
Given,
14.5% of 1,800
=(14.5/100)×1800
=261
Therefore, the answer is 261.
To know more about the percentage, visit:
https://brainly.com/question/16797504
#SPJ1
Stan ran 4 7/10 miles , which was 1 3/10 fewer miles than Matt ran. For students wrote and solve the equation to find him the number of miles that Matt Ryan which student wrote and solve the equation correctly
Answers
Answer:
Matt ran 6 miles.
Step-by-step explanation:
Stan ran 4 and 7/10 miles, and this is 1 and 3/10 fewer miles than Matt.
this means that Matt ran the following amount of miles
4 and 7/|0 + 1 and 3/10 miles:
(4 + 1) + (7/10 + 3/10) = 5 + 10/10 = 6 miles.
This would be the correct way to solve this equation.
Two partners buy a monster truck. One of them pays 3/5 of the price which is $7,800. What is the total cost of the monster truck?
Answers
Answer:
$13,000
Step-by-step explanation:
3/5 x T = 7800
T = 7800 x 5/3
= 2600 x 5
= $13,000
BRAINLIEST.
DUH.
Answer:
13000
Step-by-step explanation:
let the total cost of the truck = x
so, 3/5 of x = $7800
3x/5 = $7800
3x = $7800 × 5
3x = $39000
x = $39000/3
x = $13,000
represent the depth of a diver under water as
he swims to the surface. At what depth did
the diver begin swimming to the surface?

Answers
y = 6x + 30
To find x, substitute y = 0
Therefore,
0 = 6x + 30
-30 = 6x
x = -5
-5 is the depth
April buys soil for her flowerpots. she uses 9 kilograms of soil for her violets and 4 kilograms of soil for her tulips. she has 3,000 grams of soil left for some daisies (1 kilogram = 1,000 grams) use the drop down menus to show how much soil she bought
Answers
April bought 16 kilograms of soil in total.
To show how much soil April bought
We need to add the amounts of soil she used for her violets and tulips. Since April used kilograms for violets and tulips, we need to convert the 3,000 grams to kilograms before we can add them up.
April bought:
9 kilograms of soil for violets
4 kilograms of soil for tulips
3 kilograms of soil for daisies (since 3,000 grams is 3 kilograms)
Therefore, April bought 16 kilograms of soil in total.
Learn more about addition here : brainly.com/question/28387735
#SPJ1
How much money per candy bar is it if theres
4 for 5.50
Answers
On the following composite figure, the longer edge length is 14 millimeters. The shorter edge length is 8 millimeters. The width of the figure, at its longest point, is 11.3 millimeters. Find the area of the figure. Explain or show how you got your answer. Note: Lines that look parallel are parallel, and angles that look like right angles are right angles.

Answers
Answer:
158.2 mm^2
Step-by-step explanation:
You can think of this figure as a rectangle in which a triangle from the bottom was moved to the top.
The area of the figure is the area of the rectangle.
A = LW = 14 mm * 11.3 mm = 158.2 mm^2
Can you please tell me the sum of the question

Answers
Answer:
B) \(4i\sqrt{2}\)
Step-by-step explanation:
\(\sqrt{-2}=i\sqrt{2}\\\sqrt{-18}=i\sqrt{18}=i\sqrt{9*2}=3i\sqrt{2}\\\\\sqrt{-2}+\sqrt{-18}=i\sqrt{2}+3i\sqrt{2}=4i\sqrt{2}\)
which value of x makes this inequality true? x+9<4x
Answers
Answer:
Step-by-step explanation:
x+9
Let x, be 4
4+9=13
given condition,
x+9<4x
4+9<4(4)
13<16
The answer is:
x > 3Work/explanation:
Our inequality is:
\(\sf{x+9 < 4x}\)
Flip it
\(\sf{4x > x+9}\)
Solve
\(\sf{4x-x > 9}\)
Combine like terms
\(\sf{3x > 9}\)
Divide each side by 3
\(\sf{x > 3}\)
Hence, x > 3Find all solutions of cos()=−1/2 on the interval [−
Answers
Answer:
1.
2.
3.
4.
5.
6.
7.
8.
9.
10!!
Step-by-step explanation:
Convert the fraction below into a decimal 23/40?
Answers
Answer:
Step-by-step explanation:
23/40 = 0.575
If x+3/3 = y+2/2, then x/3 =

Answers
Answer:
y/2
Step-by-step explanation:
x/3 + 3/3 = y/2 + 2/2
x/3 + 1 = y/2 + 1
x/3 = y/2
Among all pairs of numbers whose sum is 24, find a pair whose product is as large as possible. Show the work(the steps)! Write an equation of the corresponding quadratic function. How parabola opens? What is the maximum product? Does this function has a maximum value or the minimum value? Explain. Graph the function and upload the image.
Answers
The pair of numbers that yields the maximum product when their sum is 24 is (12, 12), and the maximum product is 144. The corresponding quadratic function is P(x) = -x^2 + 24x, and the parabola opens downwards.
To find a pair of numbers whose sum is 24 and whose product is as large as possible, we can use the concept of maximizing a quadratic function.
Let's denote the two numbers as x and y. We know that x + y = 24. We want to maximize the product xy.
To solve this problem, we can rewrite the equation x + y = 24 as y = 24 - x. Now we can express the product xy in terms of a single variable, x:
P(x) = x(24 - x)
This equation represents a quadratic function. To find the maximum value of the product, we need to determine the vertex of the parabola.
The quadratic function can be rewritten as P(x) = -x^2 + 24x. We recognize that the coefficient of x^2 is negative, which means the parabola opens downwards.
To find the vertex of the parabola, we can use the formula x = -b / (2a), where a = -1 and b = 24. Plugging in these values, we get x = -24 / (2 * -1) = 12.
Substituting the value of x into the equation y = 24 - x, we find y = 24 - 12 = 12.
So the pair of numbers that yields the maximum product is (12, 12). The maximum product is obtained by evaluating the quadratic function at the vertex: P(12) = 12(24 - 12) = 12(12) = 144.
Therefore, the maximum product is 144. This quadratic function has a maximum value because the parabola opens downwards.
To graph the function, you can plot several points and connect them to form a parabolic shape. Here is an uploaded image of the graph of the quadratic function: [Image: Parabola Graph]
For more such question on function. visit :
https://brainly.com/question/11624077
#SPJ8
A package of 4 pairs of insulated costs $21.96. What is the unit price of the pairs of ?
Answers
Answer:
$5.49
Step-by-step explanation:
21.96 / 4
You will get you unit price after you do that
Find the rate of change (slope) for the given table
a -1/4
b -4
c 1/4
d 4

Answers
f(x) = x2 + 4; interval [0, 5]; n = 5; use left endpoints
Answers
Therefore, the Left Riemann Sum for this function, interval, and number of subintervals is 50.
The left endpoint rule is what?The top-left corner of these rectangles touched the y=f(x) curve. In other words, the value of f at the subinterval's left endpoint determined the height of the rectangle over that subinterval. This technique is called the left-endpoint estimate because of this.
With left endpoints and n = 5 subintervals, we may use the Left Riemann Sum formula to approximate the area under the curve of f(x) = x2 + 4 over the range [0, 5]:
Left Riemann Sum = ∑[i=1 to n] f(x_i-1) Δx
In this case, a = 0, b = 5, n = 5, and we will use the left endpoints, so:
Δx = (5 - 0)/5 = 1
Using the left endpoints, the subintervals and their left endpoints are:
[0,1],[1,2],[2,3],[3,4],[4,5]
\(so,\; x_0 = 0, x_1 = 1, x_2 = 2, x_3 = 3, x_4 = 4.\)
Now we can calculate the Left Riemann Sum:
Left Riemann Sum= \(f(x_0)\Delta x + f(x_1)\Deltax + f(x_2)\Deltax + f(x_3)\Deltax + f(x_4)\Deltax\)
= f(0)×1+f(1)×1+f(2)×1+f(3)×1 + f(4)×1
= 4+5+8+13+20
= 50
To know more about the function visit:-
brainly.com/question/12431044
#SPJ1
2 3/4 of 500grams in step by step calculator
Answers
Answer:
To calculate 2 3/4 of 500 grams, follow these steps:
1. Convert the mixed number to an improper fraction:
2 3/4 = (2 x 4 + 3)/4 = 11/4
2. Multiply the improper fraction by 500:
11/4 x 500 = (11 x 500)/4 = 2,750/4
3. Simplify the fraction by dividing the numerator and denominator by their greatest common factor, which is 2:
2,750/4 = (2 x 1,375)/(2 x 2) = 1,375/2
Therefore, 2 3/4 of 500 grams is equal to 1,375/2 grams or 687.5 grams.
Step-by-step explanation: