Write a new equation for the circle (x-3)^2 + (y+8)^2 =25 after it is shifted left 5 units and up 2 units.
Answers
Step 1: Write out the formula
Given the equation of a circle with center (h,k) and radius r, if it is shifted left by a unit and up by b unit, then the function would become
\((x-h+a)^2+(y-k-b)^2=r^2\)Step 2: Write out the given value and substitute them into the formula
In this case,
\(h=3,k=-8,a=5,b=2,r=5\)Therefore the new equation is given by
\(\begin{gathered} (x-3+5)^2+(y-(-8)-2)^2=5^2 \\ (x+2)^2+(y+8-2)^2=5^2 \\ (x+2)^2+(y+6)^2=25 \end{gathered}\)Hence, the new equation for the circle is (x+2)²+(y+6)²=25

Related Questions
The Fahrenheit temperature readings on 66 Spring mornings in New York City are
summarized in the table below. Construct and label a frequency histogram of the data
with an appropriate scale.
Temp (°F) Number of Days.
30-39
2
40-49
26
50-59
28
60-69
8
70-79
2
Graph answer Click and drag to make a rectangle. Click a rectangle to delete it.
Answers
To construct a frequency histogram based on the given temperature data, we will use the temperature ranges as the x-axis and the number of days as the y-axis.
The temperature ranges and their corresponding frequencies are as follows:
30-39: 2 days
40-49: 26 days
50-59: 28 days
60-69: 8 days
70-79: 2 days
To create the histogram, we will represent each temperature range as a bar and the height of each bar will correspond to the frequency of days.
Using an appropriate scale, we can label the x-axis with the temperature ranges (30-39, 40-49, 50-59, 60-69, 70-79) and the y-axis with the frequency values.
Now, we can draw rectangles (bars) on the graph, with the base of each rectangle corresponding to the temperature range and the height representing the frequency of days. The height of each bar will be determined by the corresponding frequency value.
For such more question on frequency
https://brainly.com/question/254161
#SPJ8
Determine which integers in the set S: {−2, −3, −4, −5} will make the inequality 2p − 8 < 5p + 4 true.
S:{−2, −3}
S:{−3, −4}
S:{−4, −5}
S:{−2, −5}
Answers
Answer:
A
Step-by-step explanation:
2p - 5p < 8 + 4
- 3p < 12
-3/-3 p > 12/-3
p > -4
-2, - 3
36 divided by m over x times 9
Answers
Answer:
Step-by-step explanation:
4/mx
PLS HELP ! ILL MARK BRAINLIST

Answers
Answer:
(x-2)^2=5 (first option)
Step-by-step explanation:
If you expand (x-2)^2, it equals x^2-4x+4. You then subtract the 5 off the right side and it becomes x^2-4x-1.
I did the work to show you what I mean. Pardon the bad handwriting ^-^'

Duane begins paying a $5,000
student loan with an annual interest rate of 6.5%
compounded monthly. He schedules monthly payments of $118.57
for 4
years.
The following table shows the first payment in the amortization schedule.
Payment
Number Loan
Amount Payment Interest Principal Remaining
Balance
1
$5,000.00
$118.57
?
What amount of Duane's first payment goes to interest?
Responses
Answers
The amount of Duane's first payment that goes to interest is approximately $26.47.
To determine the amount of Duane's first payment that goes to interest, we need to use the amortization formula for a loan.
The formula to calculate the interest portion of a loan payment is:
Interest = Remaining Balance * Monthly Interest Rate.
Let's calculate the interest for the first payment using the given information:
Loan Amount = $5,000.00
Monthly Payment = $118.57
First, we need to calculate the monthly interest rate:
Monthly Interest Rate = Annual Interest Rate / 12
= 6.5% / 12
= 0.00542
Next, we need to calculate the remaining balance after the first payment:
Remaining Balance = Loan Amount - Principal Paid
= $5,000.00 - $118.57
= $4,881.43
Finally, we can calculate the interest portion of the first payment:
Interest = Remaining Balance * Monthly Interest Rate
= $4,881.43 * 0.00542
= $26.47
For more such questions on interest
https://brainly.com/question/25720319
#SPJ8
jackson is conducting an experiment for his physics class. he attaches a weight to the bottom of a metal spring. he then pulls the weight down so that it is a distance of six inches from its equilibrium position. jackson then releases the weight and finds that it takes four seconds for the spring to complete one oscillation. Which function best models the position of the weight?a. s(t) = 6cos(2πt)b. s(t) = 6sin(π/2 t)c. s(t) = 6sin(2πt)d. s(t) = 6cos (π/2 t)
Answers
6 cos(π/2 t) is the best model for the position of the weight.
The motion of the weight on the spring can be modeled by a sine or cosine function because it oscillates back and forth around its equilibrium position.
We know that, the weight is initially pulled down 6 inches from its equilibrium position, so the function should have an amplitude of 6.
The time it takes for the spring to complete one oscillation is 4 seconds, so the period of the function is 4 seconds.
The general form of a sine or cosine function with amplitude A and period T is:
f(t) = A sin(2πt/T) or f(t)
= A cos(2πt/T)
Substituting the given values,
we get:
f(t) = 6 sin(2πt/4) or f(t)
= 6 cos(2πt/4)
Simplifying, we get:
f(t) = 6 sin(π/2 t) or f(t)
= 6 cos(π/2 t)
Therefore,
the function that best models the position of the weight is
s(t) = 6 cos(π/2 t).
So, the answer is option (D).
For similar questions on position of the weight,
https://brainly.com/question/26137753
#SPJ4
√ 7 x ( √ x − 7 √ 7 )
Answers
The expression √(7x) × (√x − 7√7) in the simplified form will be x√7 − 49√x.
What is simplification?Algebra is the study of abstract symbols, while logic is the manipulation of all those ideas.
The definition of simplicity is making something simpler to achieve or grasp while also making it a little less difficult.
The expression is given below.
⇒ √(7x) × (√x − 7√7)
Simplify the expression, then the expression is written as,
⇒ √(7x) × (√x − 7√7)
⇒ x√7 − 7 × 7√x
⇒ x√7 − 49√x
The expression √(7x) × (√x − 7√7) in the simplified form will be x√7 − 49√x.
More about the simplification link is given below.
https://brainly.com/question/12616840
#SPJ1
some please help me
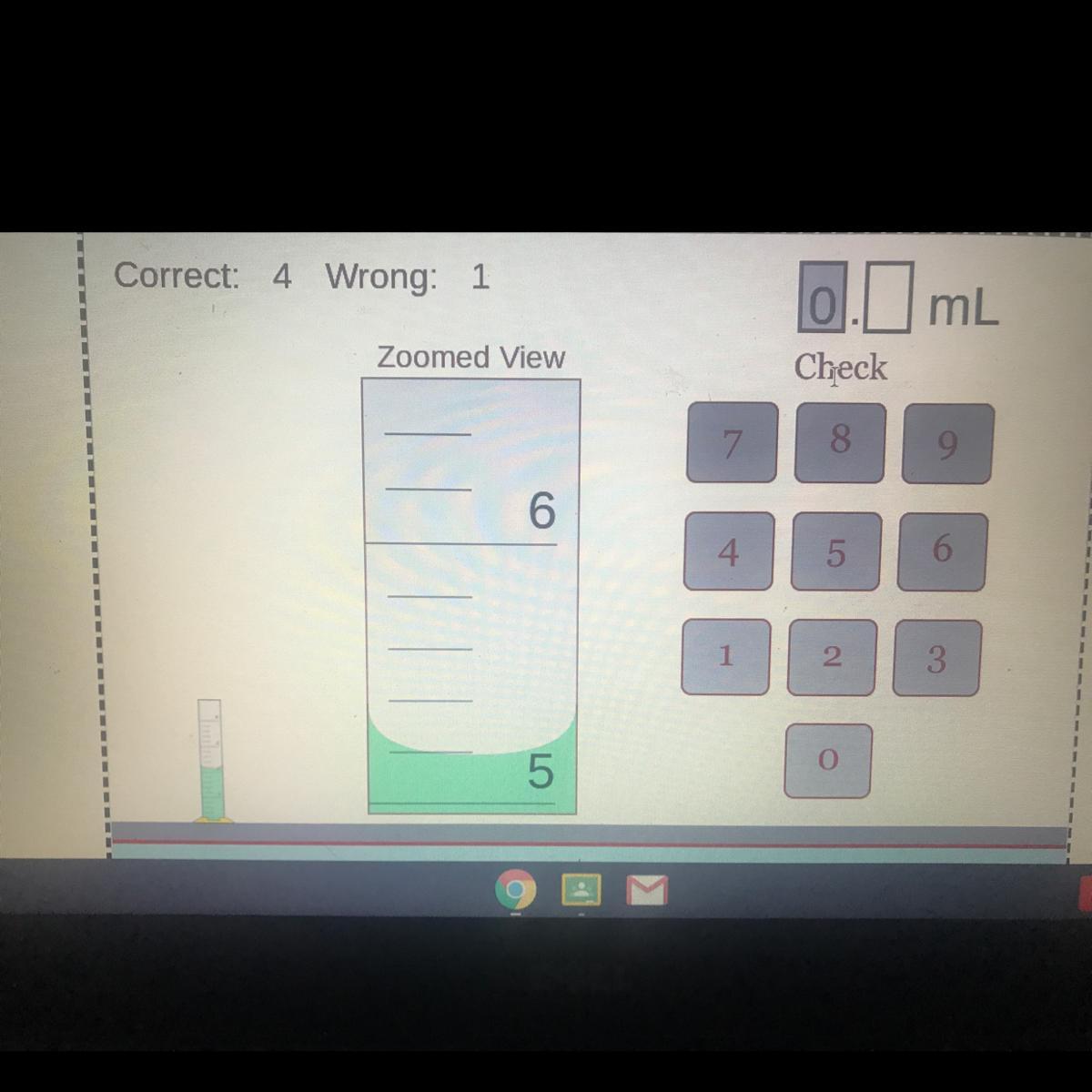
Answers
It looks like you want to find the height of the green region. If so then that would be about 5.2 mL since the top part of the green area is around the first smaller tick above the 5.
Each smaller tickmark is 1/5 = 0.2 of a full unit. Note how there are 5 smaller tickmark spaces to make up a full unit (when we go from 5 to 6, there are 5 smaller tickmark spaces we have to move)
Answer: 5.2 mLA hotel packed breakfast for each of the three guests. Each breakfast should have consisted of threeTypes of rolls, one each of nut, cheese and fruit rolls. The preparer wrapped each of the nine rollsand once wrapped, the rolls were indistinguishable from one another. She then randomly put threerolls in a bag for each of the guests. If the probability that each guest got one roll of each type ism/n where m and n are relatively prime integers, find the value of (m+n).
Answers
The probability that each guest got one roll of each type is 3/1, which is a fraction with a numerator of 3 and a denominator of 1. Since the numerator and denominator are relatively prime integers, the value of m + n is 3
The equation for the probability that each guest got one roll of each type is m/n, where m and n are relatively prime integers.
We can expand this equation to
m/n
= 3/1.
Since the numerator and denominator are relatively prime integers, we can solve for m + n by multiplying both sides of the equation by 1.
Multiplying both sides of the equation by 1 gives us
m + n = 3.
Therefore, the value of
m + n is 3.
Let m = numerator and n = denominator in the probability of m/n.
Given that each guest got one roll of each type, the probability is m/n.
The numerator and denominator are relatively prime integers, so m and n have no common factors.
Therefore,
m + n = 3.
Learn more about probability here
https://brainly.com/question/11234923
#SPJ4
Your dog is 8 years younger than your friend. In 2 years, your friend will be three times as old as your dog. How old is your dog now?
Answers
Answer:
Dog is 2 years old
Step-by-step explanation:
Let dog's age = d
Let friend's age = f
Your dog is 8 years younger than your friend:
d +8 = f
In 2 years, your friend will be three times as old as your dog:
3(d+2) = (f+2)
3d+6 = f+2
3d = f - 4
(sub in f=d+8 from above)
3d = f - 4
3d = d+8 - 4
2d = 4
d = 2
let be the amount of coffee (in ounces) that an undergraduate student at uiuc drinks per day. suppose we know that has a mean of 10 oz and a standard deviation of 5.2 oz. suppose there are 120 students in stat 107. assuming stat 107 students are a random sample, calculate the standard error of the average amount of coffee a stat 107 student drinks per day . is greater than 12.7 oz.
Answers
0.137606 the standard error of the average amount of coffee a stat 107 student drinks per day is greater than 12.7 oz.
What is standard deviation?Data dispersion in regard to the mean is quantified by a standard deviation, or "σ". Statisticians can assess if the data fits into a normal distribution or another mathematical connection using the standard deviation. The average, or mean, data point will be within one standard deviation of 68% of the data points if the data follow a normal curve.
Given that,
Standard deviation (σ) = 5.2 oz
mean (μ) = 10 oz
Number of students (n) = 120
As we know,
P ( z > 12.7 oz.) = P (z > [{x(avg.) - μ\(\sqrt{n}\)}/σ])
= P (z > [{12.7 - 10\(\sqrt{120}\)}/5.2])
= P (z > 1.86)
= 1 - P ( z < 1.86)
= 1 - 0.862394
= 0.137606
Thus, P( z > 12.7 oz.) = 0.137606
To know more about standard deviation refer to:
https://brainly.com/question/12669569
#SPJ4
Due to normality, the formula for computing z is the same for a single data value, as it is
for an average of the data values for a sample group.
True or false ?
Answers
Using the Central Limit Theorem, the statement is false, as for the averages of the data values for a sample group, the standard error is \(s = \frac{\sigma}{\sqrt{n}}\), hence, the formula is:
\(Z = \frac{X - \mu}{\frac{\sigma}{\sqrt{n}}}\)
While for a single value, it is:
\(Z = \frac{X - \mu}{\sigma}\)
In a normal distribution with mean and standard deviation , the z-score of a measure X is given by:
\(Z = \frac{X - \mu}{\sigma}\)
It measures how many standard deviations the measure is from the mean. After finding the z-score, we look at the z-score table and find the p-value associated with this z-score, which is the percentile of X. By the Central Limit Theorem, the sampling distribution of sample means of size n has standard deviation \(s = \frac{\sigma}{\sqrt{n}}\).Hence, the formulas are different, and for an average of the data values for a sample group it is:
\(Z = \frac{X - \mu}{\frac{\sigma}{\sqrt{n}}}\)
A similar problem is given at https://brainly.com/question/24663213
permieter of 2 rectangles is 54 cm.
work out the area of a square
Answers
The Area of Square is 81 cm².
let the side of the square which is length for both rectangles be a.
let the width of rectangle be x and y.
So, x+ y= a
sum of perimeters= 54
2 (a +x ) + 2 (a+ y) = 54
2a+ 2x + 2a+ 2y = 54
2a + 2a + 2(x+ y) = 54
4a + 2 (a) = 54
4a + 2a = 54
6a = 54
a= 54/6
a= 9
So, area of square
= 9 x 9
= 81 cm²
Learn more about Area here:
https://brainly.com/question/1631786
#SPJ1
Question 1-2
What is the value of a³ + b (6 + c), when a = 2, b = 3, and c = 4?
Answers
Answer:
\(\huge\boxed{\sf 38}\)
Step-by-step explanation:
Given expression:= a³ + b (6 + c)
Put a = 2, b = 3 and c = 4
= (2)³ + 3 (6 + 4)
= 8 + 3(10)
= 8 + 30
= 38\(\rule[225]{225}{2}\)
Answer:
Step-by-step explanation:
the requied answer is 38.
according to the question the value of a=2,b=3,c=4.
here,
to find the value of a³ + b (6 + c)we have to do it in steps:
step 1: solve the bracket (6+4) =10.
step 2: solve the value of a³ =8.
now put these values ,
=8+3(10)
=38.
sam can mow his yard in 5 hours. Lucy can mow the same yard in 3.5 hours. How long will it take them to mow the lawn together?
Answers
Answer:
Sam workrate 1/5
Lucy workrate 1/3.5 = reciprocal of 7/2 = 2/7
combined workrate: 1/5 + 2/7 = 17/35
they will mow the lawn in 35/17 = 2 and 1/17 hours
2 hours 3 1/2 mins
Step-by-step explanation:
100 points and brainly if correct. Put gibberish and get reported.
Task Information: Jose joined an online video game streaming service, Owl. Each year he pays a one-time yearly fee of $12.75, and it costs $0.95 per a game (g) that he plays.
Part D: In 2022, Jose received $125 for his birthday and wants to spend all of it playing video games. After paying the yearly fee, how many games (g) will he be able to play? (Create an equation and solve; show all of your work.) Write one complete sentence to explain your answer.
Part E: Use 2-3 sentences to explain how much Jose spent altogether on video games in parts B,C,D and how many video games he played from 2020-2022.
Answers
Answer:
g = 118
Step-by-step explanation:
Part D
Let g = number of games played
Given:
annual fee = $12.75cost per game = $0.95total available spend = $125⇒ 12.75 + 0.95g = 125
Solving the equation:
subtract 12.75 from both sides:
⇒ 12.75 + 0.95g - 12.75 = 125 - 12.75
⇒ 0.95g = 112.25
divide both sides by 0.95
⇒ 0.95g ÷ 0.95 = 112.25 ÷ 0.95
⇒ g = 118.1578947...
⇒ g = 118
We need to round g down to the nearest whole number, since Jose cannot pay for playing part of a game. Therefore, g = 118.
Part E
*cannot answer as part B has not been provided**
Please give an answer, and thinking. Thank you.

Answers
Answer:
see explanation
Step-by-step explanation:
- 1x + 4y = 12 , that is
- x + 4y = 12 ( add x to both sides )
4y = 12 + x ( divide each term by 4 )
y = 3 + \(\frac{1}{4}\) x
At restaurants waiters typically receive tips that average 15% of the customer’s bill. At this rate, which of the following is the closest to the trip the waiter can expect to receive if the bill was $84.63?
A) $1.27
B) $12.69
C)$97.32
Answers
Answer:
B $12.69
Step-by-step explanation:
Divide 84.63 by 100 to get 1% of the bill and then multiply the answer by 15 for 15% and round it:
\($\frac{84.63}{100} \times 15 = 12.6945$\)
The closest answer would be B $12.69.
subtract: (2x^2-6x+7) - (5x^+2x-8)
Answers
Answer:
2x^2 - 6x + 7 - (5x^2 + 2x - 8)
Distributive a -1 to each term in the parentheses.
2x^2 - 6x + 7 - 5x^2 - 2x + 8
Combine like terms.
-3x^2 - 8x + 15 is the expression after being subtracted.
Answer:
−3x² − 8x − 1Step-by-step explanation:
(2x² − 6x + 7) − (5x² + 2x +8)
To find the opposite of 5x² + 2x + 8, find the opposite of each term.
2x² − 6x + 7 − 5x² − 2x − 8
Combine 2x² and −5x² to get −3x²
−3x² − 6x + 7 − 2x − 8
Combine −6x and −2x to get −8x.
−3x² − 8x + 7 − 8
Subtract 8 from 7 to get −1.
−3x² − 8x − 1
a student spends 18 out of 35 of his pocket money on transport and fruit what is the fraction left?
Answers
To find the fraction of pocket money left after spending on transport and fruit, we need to subtract the amount spent from the total pocket money and express it as a fraction.
The student spends 18 out of 35 of his pocket money, which means he has (35 - 18) = 17 units of his pocket money left.
Therefore, the fraction of pocket money left can be written as 17/35.
Which statement is true about the local minimum of the
graphed function?
O Over the interval [-4, -2], the local minimum is 0.
Over the interval [-2, -1], the local minimum is 25.
O Over the interval [-1, 4], the local minimum is 0.
O Over the interval [4, 7], the local minimum is -7.
![Which statement is true about the local minimum of thegraphed function?O Over the interval [-4, -2],](https://brainimage.s3.us-east-005.backblazeb2.com/contents/attachments/ajE6CXYpwt37lTErWjktaboaDbRNwoW5.png)
Answers
Answer: D
Over the interval [4,7], the local minimum is -7
Choose all the fractions that are equivalent to . (Click all that apply.) 2/6, 1/2, 3/6, 8/16, 7/11, and 5/10
Answers
Answer:
1/2, 3/6, 8/16, and 5/10 are all equivalent
Step-by-step explanation:
they all equal 1/2 simplified or .50
please help me with my online classwork!

Answers
Answer:
840 cm²---------------------------
There are two triangular faces with base of 16 cm and height of 15 cm and three rectangular faces.
Find the sum of areas of all five faces:
S = 2*(1/2)*16*15 + (17*2 + 16)*12 = 240 + 600 = 840need help asap. pls somebody help.

Answers
Answer:
D
Step-by-step explanation:
why the panic ? you only need to compare the tiles with the actual terms in the equations and add them up.
x²
-x²
-x -x
x x x x (clearly that means 4x)
-1 -1 -1
1 1
so, we see it is D.
A bus company usually transports 12 000 people
per day at a ticket price of $1. The company
wants to raise the ticket price. For every $0.10
increase in the ticket price, the number of riders
per day is expected to decrease by 400. Calculate
the ticket price that will maximize revenue.
Answers
If a bus company usually transports 12 000 people per day at a ticket price of $1. The ticket price that will maximize revenue is $2 per ticket.
How to find the ticket price that will maximize revenue?Equation to find the ticket price is:
y = (12000 - 400x)(1 + .1x)
Take the derivative of the function by product rule
y' = (12000 - 400x)(.1) + (-400)(1 + .1x)
y' = 1200 - 40x - 400 - 40x
y' = 800 - 80x
Let y' = 0
0 = 800 - 80x
Solving for x
80x = 800
Divide both side by 80x
x = 800/80
x = 10
Point at x = 10
Substitute x with 10 for 1 + .1x
1 + .1(10)
= 1 + 1
= $2 per ticket
Therefore the ticket price is $2 per ticket.
Learn more about ticket price that will maximize revenue here:https://brainly.com/question/29391100
#SPJ1
y = 6 - 31
y =- 7x + 21
Answers
Solve by elimination.
multiply the lower equation by negative 1.
-y=7x-21
-y+y=o
new equation is
7x+6-52=0
6-52 is -46
-7x=-46
divide by -7
x=6.57...
plug it back in
y= 7(6.57)+21
7*6.57= 46
y=46+21
y=67
(might be wrong, I tried)
Answer:
Step-by-step explanation:
its is y=67 or it might be y=7 i
Mary won £5000 in a competition.
She used the money to pay for herself and 8 friends
to go on a holiday.
Flights cost £279 for each of them.
Accommodation cost £184 for each of them.
How much of the £5000 did she have left after paying for
flights and accommodation for herself and the 8 friends?
Answers
Answer:
$833
Step-by-step explanation:
Since there are 9 people, we need to determine the cost of accommodation and flights for all 9 people:
9(273) + 9(184) = 2457 + 1656 = 4167 for 9 people
We then subtract that amount from the amount of money she won:
5000 - 4167 = 833
Y varies inversley with x. If y = -2 when x = 6, find the value of y when x = -12.
Answers
The value of y for the inverse variation when x = -12 is derived to be equal to 1.
What is inverse variationInverse variation is a mathematical relationship between two variables, in which an increase in one variable leads to a proportional decrease in the other variable. Mathematically, inverse variation can be expressed as y = k/x, where y and x are the two variables, k is a constant of proportionality, and the product of y and x is always equal to k.
when x = 6 and y = -2, then k is derived as:
-2 = k/6
k = -12 {cross multiplication}
when x = -12, y is derived as:
y = -12/-12
y = 1
Therefore, the value of y for the inverse variation when x = -12 is derived to be equal to 1.
Read more about inverse variation here:https://brainly.com/question/10252139
#SPJ1
please help!!!
use the diagram to determine x

Answers
Answer:i think its like 40 or sum like that mb-
Step-by-step explanation:
Find the open intervals on which the function f(x)= x+10sqrt(9-x) is increasing or decreasing.

Answers
The function f(x) = x + 10√(9 - x) is increasing on the interval (-∞, 9) and decreasing on the interval (9, ∞).
To determine the intervals on which the function is increasing or decreasing, we need to find the derivative of the function and analyze its sign.
Let's find the derivative of the function f(x) = x + 10√(9 - x) with respect to x.
f'(x) = 1 + 10 * (1/2) * (9 - x)^(-1/2) * (-1)
= 1 - 5√(9 - x) / √(9 - x)
= 1 - 5 / √(9 - x).
To analyze the sign of the derivative, we need to find the critical points where the derivative is equal to zero or undefined.
Setting f'(x) = 0:
1 - 5 / √(9 - x) = 0
5 / √(9 - x) = 1
(√(9 - x))^2 = 5^2
9 - x = 25
x = 9 - 25
x = -16.
The critical point is x = -16.
We can see that the derivative f'(x) is defined for all x values except x = 9, where the function is not differentiable due to the square root term.
Now, let's analyze the sign of the derivative f'(x) in the intervals (-∞, -16), (-16, 9), and (9, ∞).
For x < -16:
Plugging in a test value, let's say x = -17, into the derivative:
f'(-17) = 1 - 5 / √(9 - (-17))
= 1 - 5 / √(9 + 17)
= 1 - 5 / √26
≈ 1 - 0.97
≈ 0.03.
Since f'(-17) is positive, the function is increasing in the interval (-∞, -16).
For -16 < x < 9:
Plugging in a test value, let's say x = 0, into the derivative:
f'(0) = 1 - 5 / √(9 - 0)
= 1 - 5 / √9
= 1 - 5 / 3
≈ 1 - 1.67
≈ -0.67.
Since f'(0) is negative, the function is decreasing in the interval (-16, 9).
For x > 9:
Plugging in a test value, let's say x = 10, into the derivative:
f'(10) = 1 - 5 / √(9 - 10)
= 1 - 5 / √(-1)
= 1 - 5i,
where i is the imaginary unit.
Since the derivative is not a real number for x > 9, we cannot determine the sign.
Combining the information, we conclude that the function f(x) = x + 10√(9 - x) is increasing on the interval (-∞, 9) and decreasing on the interval (9, ∞).
For more such questions on function, click on:
https://brainly.com/question/11624077
#SPJ8