Answers
Answer:
x=1
Step-by-step explanation:
x=1
Answer:
Hello did have actual quiz it looks like i have the same quiz could yopu send that quiz to me thanks
Step-by-step explanation:
Related Questions
(2a divided by 7) - (a-4)
Answers
Answer:
a=28/5 or 5.6
Step-by-step explanation:
2a/7=a-4
Multiple both sides of the equation by 7
2a=7a-28
Subtract 7a from both side
2a-7a=-28
Like Term
-5a=-26
Divide -5 from both side
a= 5.6
21 ÷ 3 · 5 - 6 + 2² Helpp
Answers
=4
hope to help you,have a good day
can someone help fast

Answers
6. Salary Raise. A Union negotiates for a cost-of-living raise of 3.4%. What is the raise for a union
member whose salary is $42,360. What is this person's new salary? D5
(1 Punto)
Answers
Answer:
New salary= $43,800.24Step-by-step explanation:
Step one:
Given data
the initial salary is = $42,360
the raise in percentage is =3.4%
To know the raise we need to calculate what the amount of 3.4% of $42,360 is
Step two:
=(3.4/100)*42,360
=0.034*42360
=1440.24
therefore thr raise is $1440.24
Step three:
the new salary is given as
new salary= old salary+ raise
New salary= $42,360+$1440.24
New salary= $43,800.24
answer this, please !!!

Answers
Answer:
C or R
Step-by-step explanation:
402 students were surveyed about their preferences of sports. 140 students like football, 144 students like baseball, and 42 students like both sports. how many students like exactly one of the two sports? a) 200 b) 140 c) 284 d) 98 e) 102 f) none of the above.
Answers
The students that will like exactly one of the two sports out of football and baseball is 200.
What is set theory?These are the fundamental set of set theory formulas. When there are two sets P and Q, the number of elements in one of the sets P or Q is denoted by n(P U Q). The number of elements in both sets P and Q is represented by the expression n(P ⋂Q). n(P U Q) is equal to n(P) + n(Q) - n (P Q).
Here,
F=140
B=144
F∩B=42
F-B=n(F)-n(F∩B)
=140-42
F-B=98
B-F=n(B)-n(F∩B)
=144-42
=102
So, the students that will like exactly one of the two sports,
=102+98
=200
There are 200 students who will only enjoy one of the two sports—football or baseball.
To know more about set,
https://brainly.com/question/28429487?referrer=searchResults
#SPJ4
Let k represent the length of a rectangle.
Represent the perimeter when the width is
8 less than the length.
(A) 6k-6
(B) 2k + 16
(C) 4k- 10
(D) 4k - 16
Answers
Answer:
6k 2k-6
Step-by-step explanation:
4/5 and -4/5 are same or not
Answers
Answer:
not
Step-by-step explanation:
Answer:
4/5 and -4/5 are not same because
4/5=
1 point) Compute the double integral (either in the order of integration given or with the order reversed). /2 V1 + cas"" () cos(a) drdy sin (1) Integral =
Answers
The value of the double integral is zero.
The order of integration is dr dy, which means we first integrate with respect to r and then with respect to y.
Thus, we can write the integral as:
\(\int^0_{2\pi} \int^0_{1 + cos(a)}\) r sin(θ) dr dy
Here, we have used the given limits of integration for r and y. Now, we integrate with respect to r first, treating y as a constant.
∫r sin(θ) dr = -cos(θ)r
We can substitute the limits of integration for r, which gives:
-cos(θ)(1+cos(a)) + cos(θ)(0)
Simplifying this expression, we get:
-cos(θ)(1+cos(a))
Now, we integrate this expression with respect to y, using the limits 0 to 2π for θ.
\(\int ^0_{2\pi}\) -cos(θ)(1+cos(a)) dy
We can integrate this expression by treating cos(a) as a constant and using the formula for integrating cosine functions:
Integral of cos(x) dx = sin(x) + C
Thus, we have:
(1+cos(a)) Integral from 0 to 2π of cos(θ) dy
= - (1+cos(a)) [sin(2π) - sin(0)]
= 0
To know more about integral here
https://brainly.com/question/18125359
#SPJ4
based off of this information, what conclusions can be made about the mean value theorem? this contradicts the mean value theorem since f satisfies the hypotheses on the given interval but there does not exist any c on (1, 4) such that f '(c)
Answers
The correct option is; 4: this contradicts the Mean Value Theorem since there exists a c on (1, 7) such that f '(c) = f(7) − f(1) (7 − 1) , but f is not continuous at x = 3.
Explain the term Mean Value Theorem?The Mean Value Theorem says that there occurs a point c in the interval (a,b) so that f'(c) equals the function's average rate of change throughout [a,b] if a function f is continuous just on closed interval [a,b] as well as differentiable just on open interval (a,b).The function being used is;
f(x) = (x - 3)⁻²
If we separate this function according to x, we obtain;
f'(x) = -2/(x - 3)³
Finding all c values f(7) − f(1) = f '(c)(7 − 1).is our goal.
This suggests that;
0.06 - 0.25 = -2/(c - 3)³ x 6
-0.19 = -12/(c - 3)³
(c - 3)³ = 63.157
c = 6.98
If the Mean Value Theorem holds for this function, then f must be continuous on [1,7] and differentiable on (1,7).
But when x = 3, f is not continuous, hence the Mean Value Theorem's prediction is false.
To know more about the Mean Value Theorem, here
https://brainly.com/question/19052862
#SPJ4
The complete question is-
Let f(x) = (x − 3)−2. Find all values of c in (1, 7) such that f(7) − f(1) = f '(c)(7 − 1). (Enter your answers as a comma-separated list. If an answer does not exist, enter DNE.) c = Based off of this information, what conclusions can be made about the Mean Value Theorem?
This contradicts the Mean Value Theorem since f satisfies the hypotheses on the given interval but there does not exist any c on (1, 7) such that f '(c) = f(7) − f(1) 7 − 1 . This does not contradict the Mean Value Theorem since f is not continuous at x = 3. This does not contradict the Mean Value Theorem since f is continuous on (1, 7), and there exists a c on (1, 7) such that f '(c) = f(7) − f(1) 7 − 1 . This contradicts the Mean Value Theorem since there exists a c on (1, 7) such that f '(c) = f(7) − f(1) 7 − 1 , but f is not continuous at x = 3. Nothing can be concluded.In the diagram below, dis parallel to co. What is the value of y?
CW
D
A. 120
B. 30
C. 90
D. 60

Answers
In a box of assorted cookies, 36% contain chocolate and 12% contain nuts. Of those, 8% contain both chocolate and nuts. Sean is allergic to both chocolate and nuts. Find the probability that a cookie contains chocolate or nuts (he can't eat it). (Round to two decimal places)
Answers
The probability that a randomly selected cookie is not safe for Sean to eat is 0.60.
To find the probability that a cookie contains chocolate or nuts, we need to add the probability of the cookie containing chocolate to the probability of the cookie containing nuts, and then subtract the probability of the cookie containing both chocolate and nuts. This is because if a cookie contains both chocolate and nuts, it is counted twice when we add the probability of chocolate and the probability of nuts.
Let's call the event of a cookie containing chocolate "C", the event of a cookie containing nuts "N", and the event of a cookie containing both "C∩N". Then, we can use the formula:
P(C ∪ N) = P(C) + P(N) - P(C ∩ N)
We are given that P(C) = 0.36, P(N) = 0.12, and P(C∩N) = 0.08. Substituting these values into the formula, we get:
P(C ∪ N) = 0.36 + 0.12 - 0.08 = 0.40
Therefore, the probability that a cookie contains chocolate or nuts (but not both) is 0.40.
However, Sean is allergic to both chocolate and nuts, so he cannot eat any cookies that contain either chocolate or nuts. To find the probability that a randomly selected cookie is not safe for Sean to eat, we can subtract the probability of a cookie containing neither chocolate nor nuts from 1:
P(not safe for Sean) = 1 - P(neither C nor N)
To find P(neither C nor N), we can use the complement rule:
P(neither C nor N) = 1 - P(C ∪ N)
Substituting the value we calculated earlier for P(C ∪ N), we get:
P(neither C nor N) = 1 - 0.40 = 0.60
for such more question on probability
https://brainly.com/question/13604758
#SPJ11
square root of 21 and square root of 62. must be given into 1 decimal place
Answers
Answer:
square root of 21 is 4.6
square root of 62 is 7.9
Step-by-step explanation:
square root of 21 is 4.6
square root of 62 is 7.9
What is the range of f/x )= sin x the set of all real numbers?
Answers
On solving the provided question we can say that - The Range of the given function, f(x) = sin(x) , Range = \(-1 < y < 1\)
What is Range?Range: the discrepancy between the top and bottom numbers. To get the range, locate the greatest observed value of the variable and deduct the least observed value (the minimum). The data points between the two extremes of the distribution are not taken into consideration by the range; just these two values are considered. Between the lowest and greatest numbers, there is a range. Values at the extremes make up the range. The data set 4, 6, 10, 15, 18, for instance, has a range of 18-4 = 14, a maximum of 18, a minimum of 4, and a minimum of 4.
The Range of the given function, f(x) = sin(x)
\(-1 < y < 1\)
To know more about Range visit:
https://brainly.com/question/12789483
#SPJ4
A boat is pulled in to a dock by a rope with one end attached to the front of the boat and the other end passing through a ring attached to the dock at a point 5 ft higher than the front of the boat. The rope is being pulled through the ring at the rate of 0.4 ft/sec. How fast is the boat approaching the dock when 13 ft of rope is out?
Answers
The boat is approaching the dock at a rate of approximately 0.42 ft/sec when 13 ft of rope is out.
To solve this problem, we can use the concept of related rates. Let's denote the length of the rope as "r" and the distance between the boat and the dock as "x." We are given that the rope is being pulled through the ring at a constant rate of 0.4 ft/sec.
We need to find the rate at which the boat is approaching the dock, which is the rate of change of "x" with respect to time (dx/dt). We are also given that 13 ft of rope is out (r = 13 ft).
By applying the Pythagorean theorem, we can relate the variables "r" and "x" as follows:
r² = x² + (x + 5)²
Differentiating implicitly with respect to time (t), we get:
2r(dr/dt) = 2x(dx/dt) + 2(x + 5)(dx/dt)
Simplifying the equation, we have:
dr/dt = (x(dx/dt) + (x + 5)(dx/dt))/r
We are given that dx/dt = 0.4 ft/sec and r = 13 ft. Substituting these values into the equation, we get:
dr/dt = (x(0.4) + (x + 5)(0.4))/13
Now we need to find the value of "x" when 13 ft of rope is out. Since the rope is fully extended, we have:
r = 13 ft
x + (x + 5) = 13
Simplifying this equation, we get:
2x + 5 = 13
2x = 8
x = 4 ft
Substituting this value back into the equation for dr/dt, we have:
dr/dt = (4(0.4) + (4 + 5)(0.4))/13
dr/dt = (1.6 + 9.6(0.4))/13
dr/dt = (1.6 + 3.84)/13
dr/dt = 5.44/13
dr/dt ≈ 0.42 ft/sec
Therefore, the boat is approaching the dock at a rate of approximately 0.42 ft/sec when 13 ft of rope is out.
To know more about rate visit:
https://brainly.com/question/30460463
#SPJ11
Estimate σA and σB using the loan allocation deviation formula.
A. σ(A) = 12.25% ; σ(B) = 14.14%
B. σ(A) = 17.32% ; σ(B) = 20.0%
C. σ(A) = 16.33% ; σ(B) = 14.14%
D. σ(A) = 14.14% ; σ(B) = 16.33%
Answers
The formula for allocation deviation is as follows:σA = (w1σ1^2 + w2σ2^2 + … + wσn^2)^(1/2)σB = (w1σ1^2 + w2σ2^2 + … + wσn^2)^(1/2)
Here,
σ1 = 15%
σ2 = 10%
w1 = 50%,
w2 = 50%
Substituting the values in the above formula:
σA = (0.5 × 0.15^2 + 0.5 × 0.10^2)^(1/2)
= (0.0225 + 0.0100)^(1/2)
= 0.0158 = 1.58%σB
= (0.5 × 0.15^2 + 0.5 × 0.10^2)^(1/2)
= (0.0225 + 0.0100)^(1/2)
= 0.0158
= 1.58%
Hence, the correct option is
D. σ(A) = 14.14%;
σ(B) = 16.33%.
To know more about deviation visit:
https://brainly.com/question/31835352
#SPJ11
Users can learn how to use a program by referring to the Blank______ feature within the application. quizlet
Answers
Users can learn how to use a program by referring to the interactive tutorial feature within the application, Quizlet.
Quizlet is a popular online learning platform that offers a variety of educational tools and resources, including interactive tutorials. These tutorials are designed to guide users through the process of using a particular program or application. By accessing the "Blank" feature within Quizlet, users can practice and familiarize themselves with the program's interface and functionality.
The "Blank" feature allows users to interact directly with the program by presenting them with a blank canvas or workspace where they can perform various tasks or exercises. This hands-on approach helps users develop practical skills and gain confidence in using the program effectively.
By following the step-by-step instructions provided within the interactive tutorial feature, users can learn how to navigate through the program's menus, understand its features and tools, and perform specific actions or tasks. The tutorial may include demonstrations, explanations, and interactive exercises that allow users to practice and reinforce their understanding.
Learn more about interactive tutorial feature
brainly.com/question/27383056
#SPJ11
determine the minimum distance (ft) it will take for a driver going at the speed limit to come to stop at the traffic light after the traffic light turns yellow. b) what will be minimum stopping distance if the driver was going at 45 mph (5 mph over the speed limit)? express it in ft and also as % of the distance you found in part a). c) what will be the minimum stopping distance if the driver was going at 50 mph (10 mph over the speed limit)? express it in ft and also as % of the distance you found in part a). g
Answers
The minimum stopping distance is 800 ft.
Part A: The minimum stopping distance for a driver going at the speed limit (40 mph) is given by the equation: s = v2/2a, where s is the stopping distance, v is the speed (40 mph), and a is the deceleration rate (assumed to be 10 ft/s2). Therefore, the minimum stopping distance is 800 ft.
Part B: For a driver going at 45 mph, the minimum stopping distance is given by the equation: s = v2/2a, where s is the stopping distance, v is the speed (45 mph), and a is the deceleration rate (assumed to be 10 ft/s2). Therefore, the minimum stopping distance is 925 ft, which is 15.6% greater than the stopping distance for the speed limit.
Part C: For a driver going at 50 mph, the minimum stopping distance is given by the equation: s = v2/2a, where s is the stopping distance, v is the speed (50 mph), and a is the deceleration rate (assumed to be 10 ft/s2). Therefore, the minimum stopping distance is 1250 ft, which is 56.3% greater than the stopping distance for the speed limit.
Learn more about equation here:
https://brainly.com/question/29538993
#SPJ4
2. Consider the function f(x)=x 2with domain D=R. (a) Determine the average rate of change in f(x) as x varies from x= 21to x= 23 . (b) Determine the instantaneous rate of change in f(x) at x=1.
Answers
The average rate of change in f(x) as x varies from 21 to 23 is 44. The instantaneous rate of change in f(x) at x = 1 is 2. These values represent the rates at which the function f(x) is changing over the specified intervals and points.
To determine the average rate of change in the function f(x) = x^2 as x varies from x = 21 to x = 23, and the instantaneous rate of change in f(x) at x = 1, we can apply the concept of the rate of change, which measures how a function changes with respect to its input.
(a) The average rate of change in f(x) over the interval [21, 23] is given by the formula:
Average Rate of Change = (f(23) - f(21)) / (23 - 21)
Substituting the values into the formula, we have:
Average Rate of Change = (23^2 - 21^2) / (23 - 21)
= (529 - 441) / 2
= 88 / 2
= 44
Therefore, the average rate of change in f(x) as x varies from 21 to 23 is 44.
(b) To determine the instantaneous rate of change in f(x) at x = 1, we can find the derivative of the function f(x) = x^2 and evaluate it at x = 1.
The derivative of f(x) = x^2 is given by:
f'(x) = 2x
Evaluating f'(x) at x = 1, we have:
f'(1) = 2(1)
= 2
Therefore, the instantaneous rate of change in f(x) at x = 1 is 2.
Learn more about Average Rate of Change here : brainly.com/question/13235160
#SPJ11
how many litres of oil are in the tank

Answers
Answer:
24,649 liters
Step-by-step explanation:
V = pi * h * r^2
V = pi * 250 * 100^2
V = 3.14 * 7850000
= 24,649,000 cm^3
1 liter =. 1000 cm3
X. =. 24,649,000 (cross multiplication)
24,649,000/1000=24,649 liters
need help on this, thanks

Answers
Answer:
x=15, y=7
Step-by-step explanation:
Angles that form a linear pair are supplementary, so:
\(2(5x-5)+3x-5=180 \\ \\ 10x-10+3x-5=180 \\ \\ 13x-15=180 \\ \\ 13x=195 \\ \\ x=15 \\ \\ \\ \\ 5y+5+20y=180 \\ \\ 25y+5=180 \\ \\ 25y=175 \\ \\ y=7\)
Answer:
\(x=\boxed{15}\\\\y=\boxed{7}\)
Step-by-step explanation:
Angles on a Straight Line Theorem
The sum of angles on a straight line is equal to 180°.
Solving for x:
\(\boxed{\begin{aligned}2(5x-5)^{\circ}+(3x-5)^{\circ}&=180^{\circ}\\2(5x-5)+(3x-5)&=180\\10x-10+3x-5&=180\\13x-15&=180\\13x-15+15&=180+15\\13x&=195\\13x \div 13 &=195\div 13 \\x&=15\end{aligned}}\)
Solving for y:
\(\boxed{\begin{aligned}(5y+5)^{\circ}+20y^{\circ}&=180^{\circ}\\(5y+5)+20y&=180\\5y+5+20y&=180\\25y+5&=180\\25y+5-5&=180-5\\25y&=175\\25y \div 25 &=175\div 25 \\y&=7\end{aligned}}\)
Therefore:
\(x=\boxed{15}\\\\y=\boxed{7}\)
For the series below calculate the sum of the first 3 terms, S3, and find a bound for the error. Make sure to include at least several decimals for accuracy when the problem is graded.∑
[infinity]
n
=
1
(
(
−
1
)
n
400
n
0.6
)
Answers
The sum of the first three terms in the series is -557.921 and a bound for the error is approximately 865.474.
What is series?
In mathematics, a series is the sum of the terms of a sequence. It is represented by the sigma notation (∑), which indicates that a sequence of terms is being added together.
To calculate the sum of the series and find the bounds for the error, let's break down the problem step by step.
The series can be represented as:
\(\sum_{n=1}^{\infty} [(-1)^n * 400*n^{0.6}]\)
To find the sum of the first three terms, S3, we need to calculate the values for n = 1, 2, and 3 and then sum them up.
For n = 1:
\((-1)^1 * 400 * 1^{0.6\) = -400
For n = 2:
\((-1)^2 * 400 * 2^{0.6\) = 564.189...
For n = 3:
\((-1)^3 * 400 * 3^{0.6\) = -721.110...
Now, let's calculate the sum of the first three terms, S3:
S3 = -400 + 564.189 + (-721.110) = -557.921
The sum of the first three terms, S3, is approximately -557.921.
To find a bound for the error, we can use the Alternating Series Estimation Theorem. The theorem states that the error in approximating an alternating series is less than or equal to the absolute value of the next term.
In this case, the next term of the series would be for n = 4:
\((-1)^4 * 400 * 4^{0.6\) = 865.474...
The bound for the error is given by the absolute value of this term:
|Next Term| = |865.474...| ≈ 865.474
Therefore, a bound for the error is approximately 865.474.
Learn more about sequence :
https://brainly.com/question/30262438
#SPJ4
A video game that usually costs $50 is on sale for $32 50 What percent of the regular price is the discount
Answers
Answer:
65 percent
Step-by-step explanation:
50 and is for sale at 32.50 dollars
ok to now this
32.5/50=0.65 multiply by 100
65 percent
What is the force needed to accelerate that same object to 7 m/s2? The unit of force is N (Newtons)
Answers
Answer:
252
Step-by-step explanation:
F= 36 times 7= 252
Answer:
Step-by-step explanation:
252
How many different possible outcomes are there? Please help!

Answers
48
Explanation:
6 sides on a dice, 2 sides to a coin, 4 sections on the circle spinner: 6x2x4
pleaze help me on the first 2

Answers
Answer:
1) 6:9 (9 cups of flour)
2) y = 11
Step-by-step explanation:
i did the math :)
Answer:9 cups of flour and y=11
Step-by-step explanation:
ez
Helpppppppppppppppppppppppp im not smart pls don't just say some bull i need help ill just get it deleted

Answers
Answer:
a. 6m
b. m-2
c. 5(m-2)
d. 6m +5m -10= 56
E. 11m=66
divide by 6: m=6
Maple Granola= 6$
Apple Granola= 4$
A company manufactures and sells shirts. The daily profit the company makes depends on how many shirts they sell. The profit, in dollars, when the company sells � x shirts can be found using the function � ( � ) = 7 � − 80. f(x)=7x−80. Find and interpret the given function values and determine an appropriate domain for the function.
Answers
The function f(x)=7x−80 gives the profit the company makes when it sells x shirts. The function is defined for all real numbers x such that x ≥ 0, so the domain of the function is x ≥ 0.
How to explain the functionIn order to find and interpret the given function values, we can substitute in the given values of x.
When x = 20, the profit is f(20) = 7(20) − 80 = 60. This means that when the company sells 20 shirts, they make a profit of $60.
In general, the profit the company makes is directly proportional to the number of shirts they sell. This means that the more shirts the company sells, the more profit they will make.
Learn more about functions on
https://brainly.com/question/11624077
#SPJ1
Find the volume v of the solid formed by rotating the region inside the first quadrant enclosed by y=x2 and y=5x; about the x-axis. v = ∫bah(x)dx where a= , b= , h(x)= . v=
Answers
The volume V of the solid is 500π/3 cubic units.
To find the volume V of the solid formed by rotating the region inside the first quadrant enclosed by y=x² and y=5x about the x-axis, we will use the disk method: V = ∫[πh(x)²]dx, where a and b are the limits of integration, and h(x) is the height of the solid at each x-value.
First, find the points of intersection between y=x² and y=5x by setting the two equations equal to each other: x² = 5x. Solve for x: x(x - 5) = 0, which gives x=0 and x=5. These are our limits of integration, a=0 and b=5.
Next, find the height h(x) at each x-value by subtracting the two functions: h(x) = 5x - x².
Now, we can find the volume V by integrating the area of the disks formed at each x-value: V = ∫[π(5x - x²)²]dx from 0 to 5.
V = ∫₀⁵[π(25x² - 10x³ + x⁴)]dx = π[25/3x³ - (5/2)x⁴ + (1/5)x⁵]₀⁵ = π[(125 - 625 + 3125/5) - 0] = π(500/3).
To know more about limits of integration click on below link:
https://brainly.com/question/31314427#
#SPJ11
Which graph represents a function with a domain of all numbers greater than or equal to -7 and less than 2? Your explanation should include all information about reading domain on a graph given the limitations. As well as how the different circles affects the notation on the graph when equal to and not equal to are used.
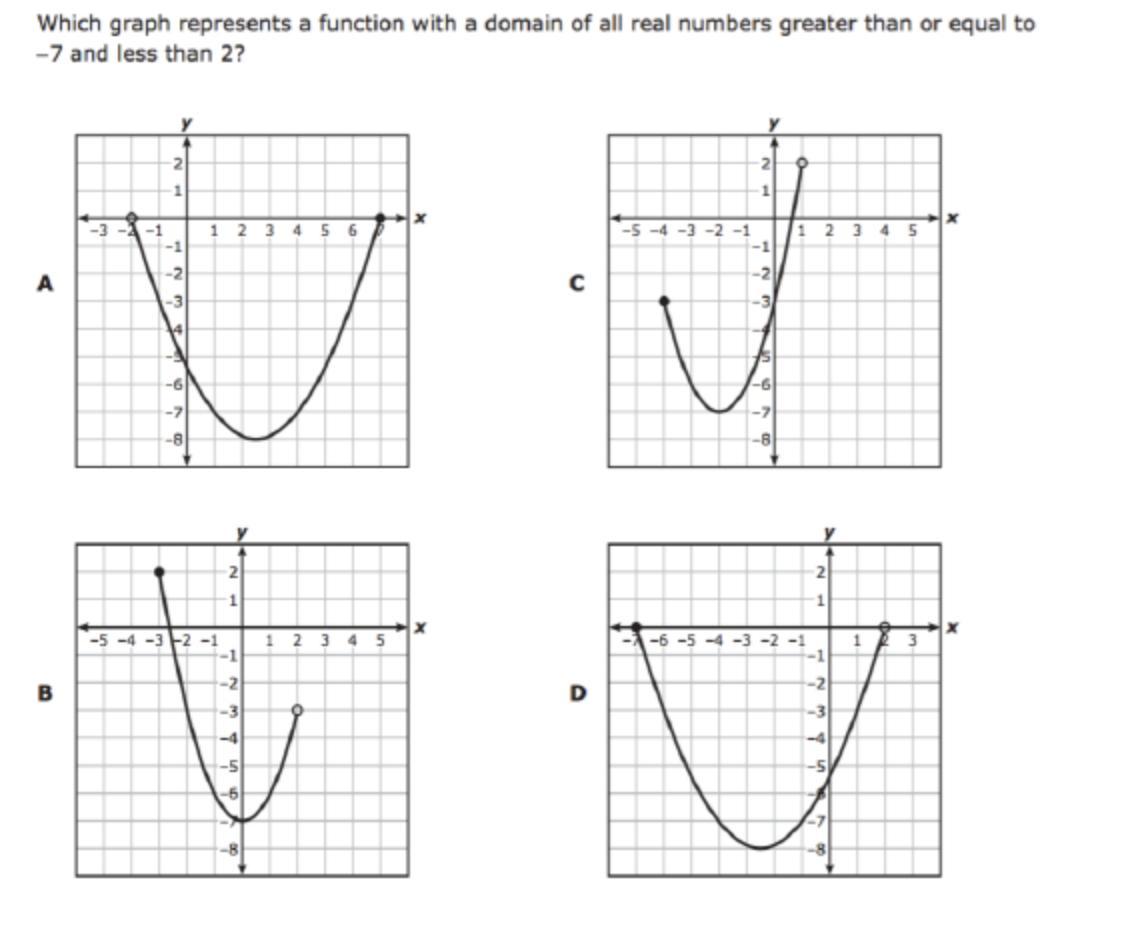
Answers
Answer: D.
Step-by-step explanation:
The way to know if it is “greater than or equal to” opposed to jsut greater than is to look at the dot. If it is filled in it is “equal to” if not it isn’t.
