work out the area of a rectangle with base, b = 9.6mm and hight, h = 2mm
Answers
Answer: 19.2mm^2
Step-by-step explanation: the area of a rectangle is simply base x height
so do 9.6 x 2 to get 19.2mm^2
Related Questions
WILL GIVE 5 STARS.
simplify the expression

Answers
Answer:
11
Step-by-step explanation:
Answer:
anwser is 7
Step-by-step explanation:14-7 equals 7 then 7x7 49 then divide 7 by 49 then 3-2 then 7x1 equaks 7
A full can of paint contains 4/5 of a gallon. Brandon used 3/4 of a can of paint to paint a doghouse. He then used 2/3 of what remained in the can to paint a door. How much paint is left in the can,in gallons?
Answers
Answer:
1/60 gallon
Step-by-step explanation:
You want to know what is left of 4/5 gallon of paint if 3/4 gallon was used to paint a doghouse, and 2/3 of the remaining amount was used to paint a door.
Amount remainingTo find the amount remaining we subtract the amount used for the doghouse from the original amount:
4/5 -3/4 = (16 -15)/20 = 1/20 . . . . . gallon
2/3 of that was used, so 1/3 of it remains:
(1/3)(1/20 gallon) = 1/60 gallon
There is 1/60 of a gallon of paint left in the can.
__
Additional comment
In a standard size gallon paint can, that's about 0.11 inches of paint in the bottom.
<95141404393>

In a classroom, 100 plastic fish are in a tub. The tub is hidden from the student view. Some fish are green, and the rest are yellow. The students know that there are 100 fish, but they don’t know how many of each color there are. The students go fishing, each time, picking a random fish from the tub, recording its color, and throwing the fish back in the tub. At the end of the day, 65 fish have been chosen, 12, green and 53 yellow. What is the best estimate you can give for the number of green fish in the number of yellow fish in the tub? Describe how to calculate this best estimate, and explain why your method of calculation makes sense in a way that a seventh grader my understand. Is your best estimate necessarily accurate? Why or why not?
Answers
The best estimate for the number of fish is that there are 82 yellow fish and 18 green fish, which you can calculate using the rule of three. This estimate is expected to be accurate.
What is the estimated number of fish of each color?This can be calculated using a rule of three as follows. Let's start with the yellow fish:
53 = 65
x = 100
53 x 100 / 65 = 82 yellow fish
Green fish:
12 = 65
x = 100
12 x 100 / 65= 18 green fish
Is this estimate accurate?This estimate is expected to be accurate; however, there might be small differences in real life such as 80 yellow fish and 20 green fish.
Learn more about estimates in https://brainly.com/question/17961193
#SPJ1
A calf raiser mixes a batch of milk replacer for 15 calves. Each calf gets two
quarts of milk replacer. If the calf raiser uses 960 oz. of replacer and needs to
add 34 as much water as milk replacer, how many ounces of water does she need?
Answers
Answer:
The calf raiser uses 960 oz of milk replacer for 15 calves, so each calf gets 960 oz / 15 = 64 oz of milk replacer.
To convert this to quarts, we need to divide by 32 (since there are 32 oz in a quart)
64 oz / 32 oz/quart = 2 quarts
Each calf gets 2 quarts of milk replacer and the calf raiser needs to add 34 as much water as milk replacer
So the total amount of water she needs is 2*34 = 68 quarts
To convert the quarts of water to ounces we need to multiply by 32 (since there are 32 oz in a quart)
68 quarts * 32 oz/quart = 2176 oz of water.
So the calf raiser needs 2176 ounces of water to mix with the milk replacer for 15 calves.
In circle O, secants ADB and AEC are drawn from external point A
such that points D, B, E, and C are on circle O. If AD = 8, AE = 6,
and EC is 12 more than BD, the length of BD is
(1) 6
(2) 22
(3) 36
(4) 48
Answers
The length of BD is 22.
In the given scenario, let's consider the following information.
AD = 8
AE = 6
EC is 12 more than BD.
To find the length of BD, we can utilize the Intercepted Arcs Theorem, which states that when two secants intersect outside a circle, the measure of an intercepted arc formed by those secants is equal to half the difference of the measures of the intercepted angles.
From the given information, we know that AD = 8 and AE = 6.
Since these are the lengths of the secants, we can use them to calculate the intercepted arcs.
First, let's find the intercepted arc corresponding to AD:
Intercepted Arc ADB = 2 \(\times\) AD = 2 \(\times\) 8 = 16
Similarly, we can find the intercepted arc corresponding to AE:
Intercepted Arc AEC = 2 \(\times\) AE = 2 \(\times\) 6 = 12
Now, we know that EC is 12 more than BD.
Let's assume the length of BD as x.
BD + 12 = EC
Now, let's consider the intercepted arcs theorem:
Intercepted Arc ADB - Intercepted Arc AEC = Intercepted Angle B - Intercepted Angle C
16 - 12 = Angle B - Angle C
4 = Angle B - Angle C.
Since Angle B and Angle C are vertical angles, they are congruent:
Angle B = Angle C.
Therefore, we can say:
4 = Angle B - Angle B
4 = 0
However, we have reached an inconsistency here.
The equation does not hold true, indicating that the given information is not consistent or there may be an error in the problem statement.
As a result, we cannot determine the length of BD based on the given information.
For similar question on length.
https://brainly.com/question/30582409
#SPJ8

Write an equationthe product of a number and 8, decreased by 3, is less than or equal to 9
Answers
The product ( multiplication) of a number (x) and 8, decreased (minus) by 3, is less or equal (
≤) to 9.
Inequality:
8x-3 ≤ 9
What sybol is true for this equation? 9/5 - 7/5
<
>
=
Answers
Answer:
I think it's 9/5 > 7/5
Step-by-step explanation:
Well, because 9 has more value than 7. Please don't be mad if I'm wrong.
Answer:
9\5 IS GREATER THAN 7\5
Step-by-step explanation:
WELL IF YOU LOOK YOU WILL SEE NINE IS GREATER THAN 7 EASY MATH HOPE I COULD HELP. PLEAAE MARK BRAINLYIEST
Please solve assignments due today

Answers
1. Initial prediction for the data set with smaller Mean Absolute Deviation was Period A. Prediction was wrong.
2. The Mean Absolute Deviation for Period A is 1.8 and Period B, 1.1
This means that period B has a smaller Mean absolute deviation.
How do we calculate the Mean Absolute Deviation?We start by finding the mean for each set;
Period A: Mean = (1×92 + 1×94 + 3×95 + 1×96 + 2×97 + 1×99 + 1×100)/10
= 960/10
= 96
Period B: Mean = (1×94 + 3×95 + 1×96 + 4×97 + 1×98)/10
= 961/10
= 96.1
Period A:
Mean Absolute Deviation = ((92-96) + (94-96) + 3(95-96) + (96-96) + 2(97-96) + (99-96) + (100-96))/10
Mean Absolute Deviation = (4 + 2 + 3 + 0 + 2 + 3 + 4)/10
Mean Absolute Deviation = 1.8
Period B:
Mean Absolute Deviation = ((94-96.1) + 3(95-96.1) + (96-96.1) + 4(97-96.1) + (98-96.1))/10
Mean Absolute Deviation = (2.1 + 3.3 + 0.1 + 3.6 + 1.9)/10
Mean Absolute Deviation = 1.1
Find more exercises on Mean Absolute Deviation;
https://brainly.com/question/10528201
#SPJ1
If one cylinder is r=3 ft and the volume is 756 feet cubed, how do I find the volume of a larger cylinder with a radius of 7feet?

Answers
Answer:
\(4116\; {\rm ft^{3}}\), assuming that the two cylinders are of the same height.
Step-by-step explanation:
The volume of a cylinder of radius \(r\) and height \(h\) is \(\pi\, r^{2}\, h\).
If the two cylinders are of the same height \(h\), the volume of the two cylinders would be proportional to the square of their radii.
Let \(r_{0}\) and \(V_{0}\) denote the radius and volume of the smaller cylinder. Similarly, let \(r_{1}\) and \(V_{1}\) denote the radius and volume of the larger cylinder. Assuming that the height of both cylinders is \(h\):
\(V_{1} = \pi\, {r_{1}}^{2}\, h\).
\(V_{0} = \pi\, {r_{0}}^{2}\, h\).
Hence, \((V_{1}) / (V_{0})\) (ratio between the volume of the larger cylinder and the volume of the smaller cylinder) would be:
\(\begin{aligned}\frac{V_{1}}{V_{0}} &= \frac{\pi\, {r_{1}}^{2}\, h}{\pi\, {r_{0}}^{2}\, h} =\frac{{r_{1}}^{2}}{{r_{0}}^{2}}\end{aligned}\).
In this question, it is given that:
the volume of the smaller cylinder is \(V_{0} = 756\; {\rm ft^{3}}\).the radius of the smaller cylinder is \(r_{0} = 3\; {\rm ft}\).the radius of the larger cylinder is \(r_{1} = 7\; {\rm ft}\).Rearrange the equation \(\begin{aligned}\frac{V_{1}}{V_{0}} &= \frac{{r_{1}}^{2}}{{r_{0}}^{2}}\end{aligned}\) to find an expression for \(V_{1}\), volume of the larger cylinder:
\(\begin{aligned}V_{1} &= \frac{{r_{1}}^{2}\, V_{0} }{{r_{0}}^{2}} \\ &= \frac{{(7\; {\rm ft})}^{2}}{{(3\; {\rm ft})}^{2}} \times (756\; {\rm ft^{3}}) \\ &= 4116\; {\rm ft^{3}} \end{aligned}\).
Lisa solved 40 math fact problems in 2 1/2 minutes.
And then she solved 80 math fact problems in 5
minutes. Which best represents her unit rate?
Answers
Answer:
Her unit rate remained the same
Step-by-step explanation:
80 is twice as much as 40. 5 minutes is twice as long as 2 1/2 minutes. Her unit rate never changed.
Answer:
her unit rate remained the same
Step-by-step explanation:
10. y=x² - 4x - 5
D =
R =
Function?
Answers
From the given expression, the factors are x+1 and x - 5 and the zeros of the function is equivalent to -1 and 5
How to factorize a function?Factorisation is defined as the breaking or decomposition of an entity. Given the quadratic equation below;
y=x² - 4x - 5
Factorize
y = x^2 - 5x + x - 5
y = x(x - 5) + 1(x - 5)
y = (x+1)(x-5)
From the given expression, the factors are x+1 and x - 5 and the zeros of the function is equivalent to -1 and 5
Learn more on factorization here: https://brainly.com/question/25829061
#SPJ1
Fill in the blank with the most appropriate term A company did a study on the physical activity level and weight gain of its employees. Age was not considered so it might be an example of an Answer 2 Points 1 Tables Keypad Keyboard Shortcuts O Confounding Variable
O Response Variable
O Explanatory Variable O Placebo
O Control Variable
Answers
A company did a study on the physical activity level and weight gain of its employees. Age was not considered, so it might be an example of a confounding variable.
A confounding variable is an unmeasured third variable that influences, or confounds, the relationship between an independent and a dependent variable. For example, in a study looking at the relationship between smoking and lung cancer, age may be a confounding variable because people who smoke tend to be older than those who do not.
This would mean that age is influencing both smoking and the risk of lung cancer, so the true effect of smoking on the risk of lung cancer cannot be determined without taking age into account. The presence of a confounding variable can distort the results of an experiment and lead to inaccurate conclusions.
Learn more about confounding variable:
https://brainly.com/question/10863424
#SPJ4
find the size of angle x 164
Answers
Note that the size of angle x = 115°. This is a problem relating to the sum of angles in a circle. See the computation below.
What is the sum of angles in a circle?The sum of angles in a circle is always equal to 360 degrees or 2π radians.
This means that the sum of the measures of the angles formed by any number of rays or line segments that meet at a common point, or vertex, and whose endpoints lie on the circle, will always add up to 360 degrees or 2π radians. This property is often used in geometry and trigonometry to solve problems involving circles and angles.
With regard to the above problem,
We are given three angles in a circle named as follows:
a) 81°
b) 164°
c) x
The above rule state that
81 + 164 + x = 360°
thus, x = 360 - 81 - 164
x = 360 -245
x = 115°
Thus the value of ∠x is 115°
Learn more about angles in a Circle:
https://brainly.com/question/29545062
#SPJ1
Full Question:
See attached image.

Which statement describes the expression 2x - 4?
Answers
Answer:
Where are the statements?
Step-by-step explanation:
Answer: -8
Step-by-step explanation:
2 times 4. Is. 8 so that equivalent to 2 times -4 =. -8
If f(7) = 8 find
f-1(8)
Answers
Answer:
34293
Step-by-step explanation:
because it 36 and 45. it is right
Identify the relationship between the angles

Answers
Answer:
∠x and ∠y are congruent or equal
Step-by-step explanation:
∠x and ∠y are congruent or equal because their vertical angles are alternate interior angles.
OR vertical angle of ∠x is congruent with ∠y because they are both corresponding angles
OR vertical angle of ∠y is congruent with ∠x because they are both corresponding angles
Write an expression to represent: 9 more than the quotient of 2 and x
Answers
Expression for given numerical is: 9+ (2/x)
Given that we have an word equation that is 9 more than the quotient of 2 and x
A quotient is a quantity produced by the division of two numbers.
Quotient of 2 and x is \(\frac{2}{x}\).
Nine(9) more than 2/x is = 9+ (2/x)
So we have an expression that is:
9+ (2/x)
learn more about quotient on brainly.com/question/16134410
#SPJ9
Gina has 32 items to ship and 11 shipping boxes. The large shipping boxes can hold 4 items each. The small shipping boxes can hold 2 items each. Gina has exactly enough boxes for her items. How many of each type of box does she have?
Answers
Answer:
Gina has 5 large shipping boxes and 6 small shipping boxes.
Step-by-step explanation:
32 items to ship and 11 shipping boxes.
Large=4 items
4 X 5 = 20
Small=2 items
2 X 6 = 12
20 + 12 = 32
Two trains leave Evas station 70 minutes apart. Train X leaves first at 1:15 pm and heads west at a speed of 106 km/h. Train Y leaves later and travels directly north at a speed of 128 km/h.
a) How far apart are these trains (along a hypotenuse) at 4:05 pm?
b) If Train Y has an unplanned stop that lasts 24 minutes, how far apart should these two trains be at 5:50 pm?
c) If both trains turn around and head back to Evas station, with Train X travelling at a new average speed of 142 km/h, which one will arrive first? Show your work and explain your thinking.
Answers
Train X is 374.39 km far apart from train Y (along the hypotenuse) at 4:05 pm and 627.009 km far apart (along the hypotenuse) at 5:50 pm.
Define hypotenuseIt goes without saying that the side opposite the right angle is the hypotenuse of a right triangle. This side of a right triangle is the longest.
given: Train X travels at a speed = 106 km/h
Train X started moving on 1:15
Train Y travels at a speed = 124 km/h
Train Y started moving on 2:25 pm
a) Time taken by train X = 2 h 15 min = 2.83 h
Speed = 106 km/h
Distance = speed * time
Distance = 106 * 2.83
Distance travelled by train X towards west is 299.98 km.
Time taken by train Y = 1 h 45 min = 1.75 h
Speed = 128 km
Distance = speed * time
Distance = 128 * 1.75
Distance travelled by train Y towards north is 224 km.
By using Pythagoras theorem,
(299.98)² + (224)² = hypotenuse²
89988 + 50176 = hypotenuse²
Hypotenuse = 140164 = 374.39
Therefore, distance between train X and train Y at 4:05 pm along hypotenuse is 374.39 km.
b) Time taken by train X = 1 h 45 min = 1.75 h
Speed = 106 km/h
Distance = speed * time
Distance = 106 * 1.75
Distance travelled by train X is 185.5 km.
Total distance travelled by X = 299.98 + 185.5 = 485.48 km
Time taken by train Y = 1 h 21 min = 1.35 h
Speed = 128 km
Distance = speed * time
Distance = 128 * 1.35
Distance travelled by train Y is 172.8 km
Total distance travelled by Y = 224 + 172.8 = 396.8 km
By using Pythagoras theorem,
(485.48)² + (396.8)² = hyopotenuse²
235690.84 + 157450.24 = hypotenuse²
393141.08 = hypotenuse²
Hypotenuse = 627.009
Distance between train X and train Y at 5:50pm is 627.009 km.
c) Distance of train X from Evas station = 485.48km
Speed = 142 km/h
Time taken = distance / speed
Time taken = 485.48 / 142
Time taken by train X to reach station is 3.42 h
Distance of train Y from Evas station = 396.8 km
Speed = 128 km/h
Time taken = distance / speed
Time taken = 396.8 / 128
Time taken by train Y to reach station is 3.1 h
Therefore, train Y will arrive station first.
To know more about Pythagoras theorem visit:
https://brainly.com/question/343682
#SPJ1
Triangle ABC has these side measurements:
AB = 17
BC = 18
AC = 21
Order the angles of the triangle from largest measure to smallest measure.
Answers
Answer:
the ordered measure of the triangle from largest are:- 21, 18, 17
Let T: R2→R2 be the linear transformation that first rotates points clockwise through 30∘ and then reflects points through the line y=x. Find the standard matrix A for T.
A = ?
Answers
The standard matrix A is [ (1/2, √3/2) (√3/2, -1/2) ]
To find the standard matrix of a linear transformation, we need to find the images of the standard basis vectors under the transformation.
The standard basis vectors in R2 are (1,0) and (0,1). Let's find their images under T.
The image of (1,0) under a 30∘ clockwise rotation is (√3/2, 1/2). The image of this under reflection through the line y=x is (1/2, √3/2).
The image of (0,1) under a 30∘ clockwise rotation is (-1/2, √3/2). The image of this under reflection through the line y=x is (√3/2, -1/2).
The standard matrix of T is then the matrix whose columns are the images of the standard basis vectors:
A = [ (1/2, √3/2) (√3/2, -1/2) ]
= \(\left[\begin{array}{cc}1/2&\sqrt{3} /2\\\sqrt{3} /2&-1/2\end{array}\right]\)
To know more on linear transformation
https://brainly.com/question/30466131
#SPJ4
The rectangle is three times its width.
If the perimeter of the rectangle is 80in, find its length and width.
Answers
Answer:
Length= 30 in
Width= 10 in
Step-by-step explanation:
Let the width of the rectangle be x in.
Length of rectangle
= 3 (width)
= 3x
Perimeter of rectangle= 2(length) +2(width)
80= 2(3x) +2(x)
80= 6x +2x
8x= 80 (simplify)
x= 80 ÷8 (÷8 on both sides)
x= 10
Thus width of rectangle= 10 in
Length of rectangle
= 3(10)
= 30 in
Mary spends 2 2 3 hours on math homework every week. She also spends 3 1 3 hours on art homework every week. How much time does Mary spend in total on math and art over 4 weeks?
Answers
Answer: This is the answer. please give me the brainliest. Thanks

Plz help what’s the length of the side
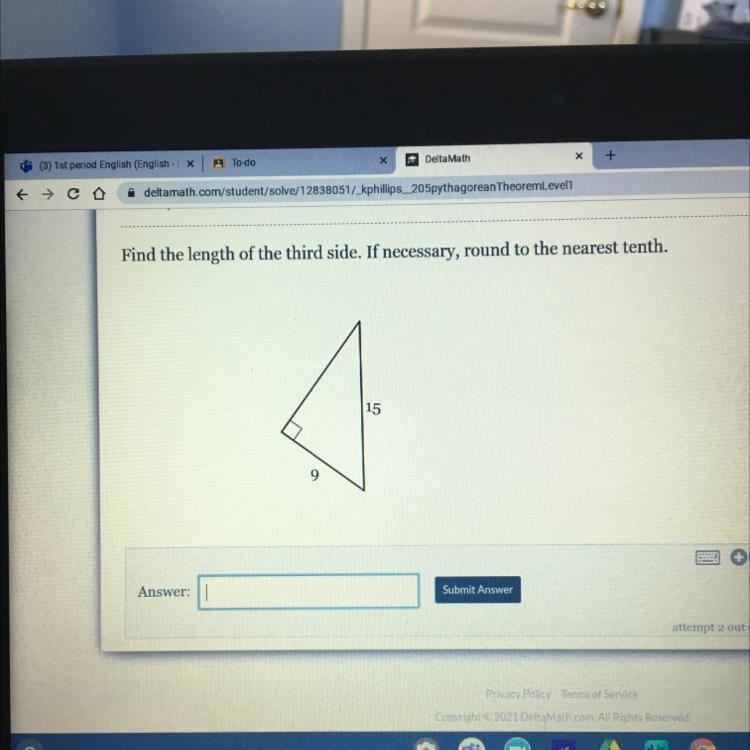
Answers
Answer:
12
Step-by-step explanation:
Pythagoras Theorem is clearly used in this question.
To Calculate the Hypotenuse:
C = \(\sqrt{a^2+b^2}\)
The Adjacent angle has already given as 9, so you can factor that into the question.
In Order to calculate the Opposite angle you need to use the following formula.
\(b = \sqrt{c^2-a^2}\)
With the integers we already have for both Hypotenuse and Adjacent factored in this will be your equation:
\(b = \sqrt{15^2-9^2} = 12\)
Therefore you answer is 12, Hope this helps, feel free to make as brainilest.
show that d^2y/dx^2=-2x/y^5, if x^3 + y^3=1
Answers
Answer:
y³ + x³ = 1
First, differentiate the first time, term by term:
\({3y^{2}.\frac{dy}{dx} + 3x^{2}} = 0 \\\\{3y^{2}.\frac{dy}{dx} = -3x^{2}} \\\\\frac{dy}{dx} = \frac{-3x^{2}}{3y^{2}} \\\\\frac{dy}{dx} = \frac{-x^{2}}{y^{2}}\)
↑ we'll substitute this later (4th step onwards)
Differentiate the second time:
\(3y^{2}.\frac{dy}{dx} + 3x^{2} = 0 \\\\3y^{2}.\frac{d^{2} y}{dx^{2}} + 6y(\frac{dy}{dx})^{2} + 6x = 0 \\\\3y^{2}.\frac{d^{2} y}{dx^{2}} + 6y(\frac{dy}{dx})^{2} = - 6x \\\\3y^{2}.\frac{d^{2} y}{dx^{2}} + 6y(\frac{-x^{2} }{y^{2} })^{2} = - 6x \\\\3y^{2}.\frac{d^{2} y}{dx^{2}} + 6y(\frac{x^{4} }{y^{4} }) = - 6x \\\\3y^{2}.\frac{d^{2} y}{dx^{2}} + \frac{6x^{4} }{y^{3} } = - 6x \\\\3y^{2}.\frac{d^{2} y}{dx^{2}} = - 6x - \frac{6x^{4} }{y^{3} } \\\\\)
\(3y^{2}.\frac{d^{2} y}{dx^{2}} = - \frac{- 6xy^{3} - 6x^{4} }{y^{3}} \\\\\frac{d^{2} y}{dx^{2}} = - \frac{- 6xy^{3} - 6x^{4} }{3y^{2}. y^{3}} \\\\\frac{d^{2} y}{dx^{2}} = - \frac{- 2xy^{3} - 2x^{4} }{y^{5}} \\\\\frac{d^{2} y}{dx^{2}} = - \frac{-2x (y^{3} + x^{3})}{y^{5}} \\\\\frac{d^{2} y}{dx^{2}} = - \frac{-2x (1)}{y^{5}} \\\\\frac{d^{2} y}{dx^{2}} = - \frac{-2x}{y^{5}}\)
) In a geometric progression, the sum of the first two terms is equal to 16. The sum to infinity is equal to 25. Find the possible values of the first term.
Answers
There are no possible real values for the first term 'a' that satisfy both equations.
Let's denote the first term of the geometric progression as 'a' and the common ratio as 'r'.
The sum of the first two terms can be expressed as:
a + ar = 16
To find the sum to infinity, we can use the formula:
Sum to infinity = a / (1 - r)
Given that the sum to infinity is 25, we have:
25 = a / (1 - r)
We now have two equations:
a + ar = 16
a / (1 - r) = 25
We can solve these equations simultaneously to find the possible values of 'a'.
From the first equation, we can factor out 'a' to get:
a(1 + r) = 16
Dividing both sides of the second equation by 25, we have:
a / (1 - r) = 1
We can rearrange this equation to get:
a = 1 - r
Substituting this expression for 'a' in the first equation, we get:
(1 - r)(1 + r) = 16
Expanding the equation, we have:
1 - r^2 = 16
Rearranging the terms, we get:
r^2 = -15
Since we are dealing with a geometric progression, the common ratio 'r' must be a real number. However, we observe that r^2 = -15 has no real solutions. Therefore, there are no possible real values for the first term 'a' that satisfy both equations.
for such more question on real value
https://brainly.com/question/27371101
#SPJ8
PLEASE FAST
Solve the equation for t.
4(t – 2.9) ≥ 3.6
t ≥ 17.3
t ≥ 11.5
t ≥ 3.8
t ≥ 1.6
Answers
Answer:3.8
Step-by-step explanation:
Find an equation for the perpendicular
bisector of the line segment whose
endpoints are (7, 3) and (-5, 9).
Answers
Therefore , the solution of the given problem of equation comes out to be the equation of the perpendicular bisector of that line segment (7, 3) and (-5, 9) is y = 2x + 4.
Explain equation.Complex algorithms frequently employ variable words to demonstrate coherence between two opposing assertions. Equations are academic expressions that are used to demonstrate the equality of different academic figures. In this case, leveling generates b + 7 rather than another algorithm that could analyze data provided by y + 7, split 12 into two parts, and create y + 7.
Here,
The midpoint formula can be used to determine the midpoint of the line segment whose ends are (7, 3) and (-5, 9):
=> ((7 + (-5))/2, (3 + 9)/2) = (1, 6)
the middle is thus (1, 6). The slope of the line going through (7, 3) and must now be determined. (-5, 9). The slope method is used to:
=>slope = (9 - 3)/(-5 - 7) = -6/12 = -1/2
The equivalent of -1/2 in the negative is 2.
=> y - y1 = m(x - x1)
where (x1, y1) is a location on the line and m denotes the slope. When we replace m = 2 with (1, x1, y1) = (1, 6), we obtain:
=> y - 6 = 2(x - 1)
By enlarging and condensing, we obtain:
=> y - 6 = 2x - 2
=> y = 2x + 4
the line segment whose ends are and the equation of the perpendicular bisector of that line segment (7, 3) and (-5, 9) is y = 2x + 4.
'To know more about equation visit:
https://brainly.com/question/649785
#SPJ1
What is the area of figure?
A. 56 square meters
B. 80 square meters
C. 120 square meters
D. 136 square meters
E. 152 square meters
(quiz help )

Answers
Answer:
D
Step-by-step explanation:
8×16=128
2×4=8
128+8=136m^2
answer: D
m=4; (2,3) hghh
mmmmmmmmmmmm m mmmmmmmmmmmm
Answers
Answer:
i do not understand your question
Step-by-step explanation: