Answers
Answer:
896+32=928in
Step-by-step explanation:
Related Questions
36. You drop a ham that weighs 9.25 lbs from a height of 1.45m. Right before it hits the ground, it has a velocity of 5.33m/s. Given that the impact of the ham and the tile floor has a coefficient of restitution or 0.35, how high will it bounce after impact? (1 point)
Answers
The ham will bounce to a height of 0.16 meters after the impact.
Define Potential Energy.It is the energy that an object possesses by virtue of its position or configuration, or as a result of its composition. The potential energy of an object can be converted into kinetic energy, which is the energy of motion.
initial potential energy of the ham:
PE = mgh
where m is the mass of the ham, g is the acceleration due to gravity, and h is the initial height from which the ham is dropped. Substituting the given values, we get:
PE = (9.25 lbs)× (1 kg/2.205 lbs) × (9.81 m/s²) × (1.45 m) ≈ 61.8 J
At the moment just before the ham hits the ground, all of this potential energy is converted into kinetic energy:
KE = (1/2)mv²
where v is the velocity of the ham just before impact. Substituting the given values, we get:
KE = (1/2) × (9.25 lbs) × (1 kg/2.205 lbs)×(5.33 m/s)²≈ 87.8 J
After the impact, some of this kinetic energy is lost due to the coefficient of restitution, which is the ratio of the velocity after impact to the velocity just before impact:
e = v'/v
where v' is the velocity after impact. Substituting the given values, we get:
0.35 = v'/5.33
Solving for v', we get:
v' ≈ 1.86 m/s
Now, we can use the conservation of energy to find the maximum height to which the ham bounces. At this point, all of the remaining kinetic energy has been converted back into potential energy:
KE = (1/2)mv'² = mgh'
where h' is the maximum height to which the ham bounces. Substituting the given values, we get:
(1/2) × (9.25 lbs) × (1 kg/2.205 lbs) ×(1.86 m/s)² = (9.81 m/s²) ×h'
Solving for h', we get:
h' ≈ 0.16 m
Therefore, the ham will bounce to a height of approximately 0.16 meters (or 16 centimeters) after the impact.
To know more about restitution, visit:
https://brainly.com/question/15869415
#SPJ1
Solve the inequality for w.
w+7<20
Simplify your answer as much as possible.
0
Answers
Answer:
w<13
Step-by-step explanation:
Works identically to a normal single-variable equation.
Subtract 7 on both sides in order to isolate w--->w+7-7<20-7
The answer (which cannot be simplified any further) is w<13.
Answer:
w < 1`3
Step-by-step explanation:
Isolate the variable w on one side of the inequality sign.
w+7<20
w<20 - 7
w<13.
One brand of cola co fizz is sold in packs of 4*500ml for 2.50 another brand colo is sold in packs of 10 330mlfo $2 which brand is more expensive
Answers
Based on the given information, the second brand, Cola, is the more affordable option in terms of cost per milliliter compared to Co Fizz.
To determine which brand of cola is more expensive, we need to compare the cost per unit volume for each brand.
For the first brand, Co Fizz, a pack contains 4 bottles, and each bottle has a volume of 500 ml. The cost of the pack is $2.50. Therefore, the total volume in a pack is 4 * 500 ml = 2000 ml. To find the cost per milliliter (ml), we divide the total cost by the total volume: $2.50 / 2000 ml = $0.00125 per ml.
For the second brand, Cola, a pack contains 10 bottles, and each bottle has a volume of 330 ml. The cost of the pack is $2. Therefore, the total volume in a pack is 10 * 330 ml = 3300 ml. To find the cost per milliliter (ml), we divide the total cost by the total volume: $2 / 3300 ml ≈ $0.000606 per ml.
Comparing the two brands, we can see that the cost per milliliter for Co Fizz is $0.00125, while the cost per milliliter for Cola is approximately $0.000606.
Since the cost per milliliter for Co Fizz is higher than the cost per milliliter for Cola, it can be concluded that Co Fizz is more expensive in terms of price per unit volume.
For more such question on brand. visit :
https://brainly.com/question/29129317
#SPJ8
prove that the roots of x2+(1-k)x+k-3=0 are real for all real values of k
Answers
The roots of x^2 + (1 - k).x+k-3 = 0 are real for all real values of k
The equation is given as:
x^2 + (1 - k).x+k-3 = 0
For an equation to have real root, then the following must be true:
\(b^2 \ge 4ac\)
In x^2 + (1 - k).x+k-3 = 0, we have:
a = 1
b = 1 - k
c = k - 3
So, we have:
\((1 - k)^2 \ge 4 * 1 * (k - 3)\)
Evaluate
\(1 - 2k + k^2 \ge 4k - 12\)
Collect like terms
\(k^2 - 2k - 4k + 1 + 12 \ge 0\)
\(k^2 - 6k + 13 \ge 0\)
Using a graphing calculator, the value of k is all real numbers
Hence, the roots of x^2 + (1 - k).x+k-3 = 0 are real for all real values of k
Read more about real values at:
https://brainly.com/question/6499629
Find the mean, median, mode 1. 40, 38,29,34,37, 22, 15, 38 2. 26, 32, 12, 18, 11, 14, 21, 12,27 3. 3,3,4,7,5,7,6,7,8,8,8. 9,8, 10, 12, 9, 15, 15
NEED THE ANSWER ASAP
NONSENSE, REPORT
i will (brainliest) if it's correct!!!

Answers
Mean: 34.125, Median: 31.5, Mode: 38
Mean: 19.222, Median: 18, No mode
Mean: 8.611, Median: 8, Mode: 8
Let's find the mean, median, and mode for each set of numbers:
Set: 40, 38, 29, 34, 37, 22, 15, 38
Mean: To find the mean, we sum up all the numbers and divide by the total count:
Mean = (40 + 38 + 29 + 34 + 37 + 22 + 15 + 38) / 8 = 273 / 8 = 34.125
Median: To find the median, we arrange the numbers in ascending order and find the middle value:
Arranged set: 15, 22, 29, 34, 37, 38, 38, 40
Median = (29 + 34) / 2 = 63 / 2 = 31.5
Mode: The mode is the number(s) that appear(s) most frequently in the set:
Mode = 38 (appears twice)
Set: 26, 32, 12, 18, 11, 14, 21, 12, 27
Mean: Mean = (26 + 32 + 12 + 18 + 11 + 14 + 21 + 12 + 27) / 9 = 173 / 9 ≈ 19.222
Median: Arranged set: 11, 12, 12, 14, 18, 21, 26, 27, 32
Median = 18
Mode: No mode (all numbers appear only once)
Set: 3, 3, 4, 7, 5, 7, 6, 7, 8, 8, 8, 9, 8, 10, 12, 9, 15, 15
Mean: Mean = (3 + 3 + 4 + 7 + 5 + 7 + 6 + 7 + 8 + 8 + 8 + 9 + 8 + 10 + 12 + 9 + 15 + 15) / 18 ≈ 8.611
Median: Arranged set: 3, 3, 4, 5, 6, 7, 7, 7, 8, 8, 8, 8, 9, 9, 10, 12, 15, 15
Median = 8
Mode: Mode = 8 (appears 4 times)
Mean: 34.125, Median: 31.5, Mode: 38
Mean: 19.222, Median: 18, No mode
Mean: 8.611, Median: 8, Mode: 8
For more questions on Mean
https://brainly.com/question/1136789
#sPJ8
Use the permutation formula below to find the number of outcomes when n = 5
and r= 2.
n!
(n,r)!
Answers
Answer:
20.
Step-by-step explanation:
5! / (n - r)!
= (5*4*3*2*1) / 3*2*1
= 5*4
= 20.
Aye yo I need this thanks

Answers
Answer:
aye yo its 4
Step-by-step explanation:
Answer:
Here, we use the law of alternate interior angles. <3 and <6 are are alternat.e interior angles, meaning they have the same measure. We can solve x by using this equation:
3x-2=34
Add 2 to both sides
3x-2+2=34+2
3x=36
Divide both sides by 3
3x/3=36/3
x=12
2. Here, we use the law of consecutive interior angles. <4 and <6 are consecutive interior angles, meaning that the sum of their measures is equal to 180 degrees. We can solve x by using this equation:
-2x+20+6x+20=180
4x+40=180
Subtract both sides by 40
4x+40-40=180-40
4x=140
Divide both sides by 4
4x/4=140/4
x=35
3. Here, we use the law of alternate exterior angles. <7 and <2 are alternate exterior angles, meaning that their measures are the same. We can solve x by using this equation:
4x+3=x+15
Subtract both sides by 3
4x+3-3=x+15-3
4x=x+12
Subtract both sides by x
4x-x=x+12-x
3x=12
Divide both sides by 3
3x/3=12/3
x=4
4. Here, we use the law of alternate interior angles (again). <4 and <5 are alternate interior angles, meaning that they have the same measure. We can solve x by using this equation:
5x-3=3x+17
Add both sides by 3
5x-3+3=3x+17+3
5x=3x+20
Subtract both sides by 3x
5x-3x=3x+20-3x
2x=20
Divide both sides by 2
2x/2=20/2
x=10
5. Here, we use the law of consecutive interior angles (again). <3 and <5 are consecutive interior angles, meaning that the sum of their measures is equal to 180 degrees. We can solve x by using this equation:
5x-6+19=180
5x+13=180
Subtract both sides b.y 13
5x+13-13=180-13
5x=167
Divide b.oth sides by 5
5x/5=167/5
x=33.4
I hope this helps!
Step-by-step explanation:
2x - y = -2,X + y = -1
Answers
Answer:
x=-1, y=0
Step-by-step explanation:
Hope this is right!!
Lisa and Krystal are planning trips to ten countries this year. They have 14 countries on their bucket list, in how many ways can they decide which countries to SKIP? 643 24,024 683 1,001
Answers
Answer:
1,001 ways for them to decide.
Step-by-step explanation:
The order in which they will visit the countries is not important, so we use the combinations formula to solve this question.
Combinations formula:
\(C_{n,x}\) is the number of different combinations of x objects from a set of n elements, given by the following formula.
\(C_{n,x} = \frac{n!}{x!(n-x)!}\)
In this question:
10 countries from a set of 14. So
\(C_{14,10} = \frac{14!}{10!(14-10)!} = 1001\)
1,001 ways for them to decide.
Use the graph to answer the question.
Graph of polygon ABCD with vertices at negative 2 comma negative 1, 0 comma negative 4, 4 comma negative 4, 2 comma negative 1. A second polygon A prime B prime C prime D prime with vertices at 5 comma negative 1, 7 comma negative 4, 11 comma negative 4, 9 comma negative 1.
Determine the translation used to create the image.
7 units to the right
3 units to the right
7 units to the left
3 units to the left
Answers
The translation used to create the image of the second polygon is A, 7 units to the right.
How to determine translation?To determine the translation used to create the image of the second polygon (A' B' C' D') from the original polygon (ABCD), compare the corresponding vertices.
Original polygon (ABCD):
A (-2, -1)
B (0, -4)
C (4, -4)
D (2, -1)
Image polygon (A' B' C' D'):
A' (5, -1)
B' (7, -4)
C' (11, -4)
D' (9, -1)
To find the translation, calculate the horizontal and vertical differences between the corresponding vertices.
Horizontal difference:
For point A: A'x - Ax = 5 - (-2) = 7
For point B: B'x - Bx = 7 - 0 = 7
For point C: C'x - Cx = 11 - 4 = 7
For point D: D'x - Dx = 9 - 2 = 7
Vertical difference:
For point A: A'y - Ay = -1 - (-1) = 0
For point B: B'y - By = -4 - (-4) = 0
For point C: C'y - Cy = -4 - (-4) = 0
For point D: D'y - Dy = -1 - (-1) = 0
From the calculations, see that the horizontal difference is 7 units for all the corresponding vertices, while the vertical difference is 0 units for all the corresponding vertices.
Therefore, the translation used to create the image of the second polygon is 7 units to the right.
Find out more on polygon here: https://brainly.com/question/1592456
#SPJ1
Mathematical form of the question:
Use the graph to answer the question.
Graph of polygon ABCD with vertices at A (-2, -1), B (0, -4), C (4, -4), D (2, -1). A second polygon A' (5, -1), B' (7, -4), C' (11, -4), D' (9, -1).
Determine the translation used to create the image.
7 units to the right
3 units to the right
7 units to the left
3 units to the left
What is the maximum of f(x)=sin(x)
Answers
Answer:
1
Step-by-step explanation:
The maximum of f(x) = sin(x) is 1. The sine function has a range of -1 ≤ sin(x) ≤ 1. The sine function oscillates between -1 and 1, reaching a maximum of 1 when x = π/2 and a minimum of -1 when x = -π/2. If you look at a graph of
y = sin(x) you can see this.
Answer: The Maximum Value of f(x)=sin(x) is 1 , when x=90°.
Step-by-step explanation:
Property of Sine function:
Sin(x)=0 when x=90°,180°,360°The maximum and Minimum value of Sin(x) is 1 and -1 respectively, when and x=270° respectively.The range of values of sin(x) is -1 to 1.Read more on the Sine function:
https://brainly.com/question/21902442
https://brainly.com/question/29529184
https://brainly.com/question/23214084
Bryce has $16 more than Corey. Both have a combined total of $50. How much money does Bryce have.
Answers
Answer:
$33
Step-by-step explanation:
Let the amount of money Corey has be $x.
Amount of money Bryce have= $(x +16)
Total amount= $50
$x +$(x +16)= $50
2x +16= 50
2x= 50 -16
2x= 34
Divide both sides by 2:
x= 34 ÷2
x= 17
Amount of money Bryce have
= $(17 +16)
= $33
Enter your answer and show all the steps that you use to solve this problem in the space provided.
What else must you know to prove the triangles congruent by SAS?

Answers
Answer:
Let do this..
Step-by-step explanation:
ABCD is a parallelogram - 1
In ∆ADC and ∆CBA
AC=AC (Common)
<DAC=<BCA (Given)
AD=CB (From 1)
Therefore, ∆ADC = ∆CBA (By SAS)
If you toss 2 coins at the same time what is the probability of getting at least one head
Answers
Step-by-step explanation:
tossing 2 coins at the same time, or one coin twice is the same scenario.
anyway, a probability is always the ratio
desired cases / all possible cases
when having 2 coin tosses, there are 2×2 = 4 total possible results (each toss has 2 possibilities, so 2 tosses have them 2×2 = 4 possibilities) :
head head
head tails
tail head
tail tails
how many of these 4 possible cases show at least one head ?
3 : head-head, head-tails, tails-head
so the probability to get at least one head is
3/4 = 0.75
formally calculated we would get this by saying either
this is NOT 2 times tail.
the probability of 2 times tails is
1/2 × 1/2 = 1/4 = 0.25
the probability for NOT 2 times tails is then
1 - 0.25 = 0.75
or by saying
this is either heads on the first coin and tails on the other, or tails on the first coin and heads on the other, or heads on both.
the probability of heads on the first and tails on the other coin is
1/2 × 1/2 = 1/4
the probability of tails on the first and heads on the other coin is
1/2 × 1/2 = 1/4
the probability of heads on both coins is
1/2 × 1/2 = 1/4
so, the total probability of all 3 cases is
1/4 + 1/4 + 1/4 = 3/4 = 0.75
you see : for an exclusive "or" condition we add the probabilities. for an exclusive "and" condition we multiply the probabilities.
High Point Clinic is projecting 50,000 visits in 2019. The clinic uses 0.5 hours of labor per visit at a cost of $30 per hour and 1.5 units of supplies per visit at a cost of $2 per unit. What is the clinic's budgeted variable costs for 2019?
A. 1,100,000
B. 1,250,000
C. 1,600,000
D. 900,000
Answers
$125,000 in total that would be $750,000 + $125,000 =$875,000 but is a budget so you need to have some money to keep your business running you don’t want to have $0 so they would have $900,000 for there budget
Answer: $900,000
Hey can anyone help me understand how to graph this?

Answers
Answer:
Step-by-step explanation:
?
The seller of a watch marked up the price by 25%, and the new price is $325.00. What was the watch’s original price before the markup?
Answers
solve for x/5 - g = a for x

Answers
Add g to both sides
Multiply both by 5 (equation)
Simplify both sides
I don’t under this .
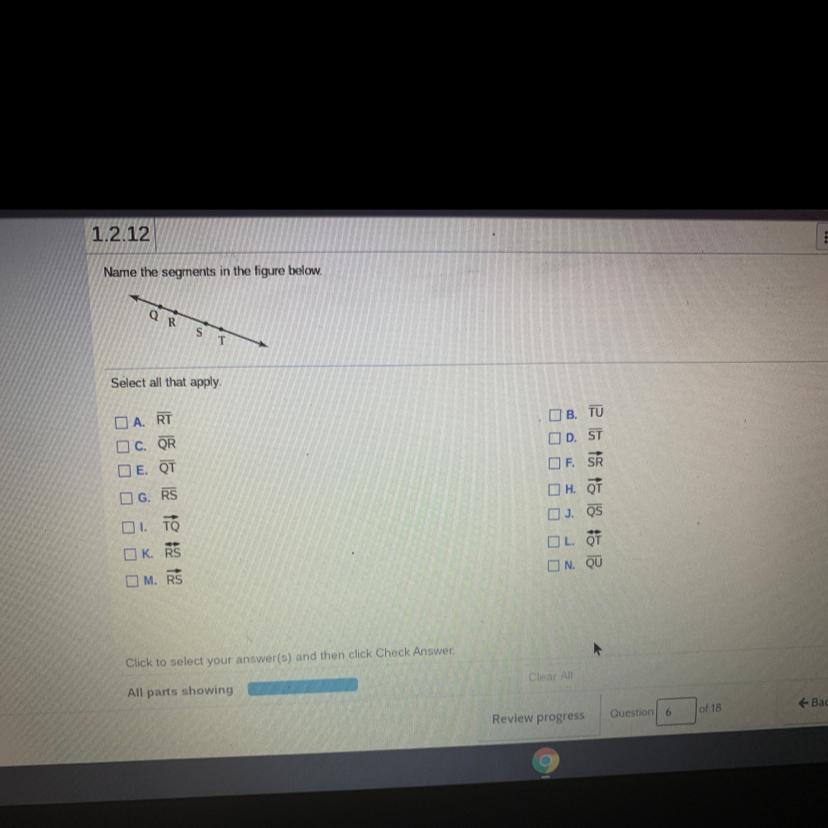
Answers
Answer:
The answer is QR,RS, and ST
Step-by-step explanation:
i hope this helps .
Explanation:
Suppose that a study of elementary school students reports that the mean age at which children begin reading is 5.4 years with a standard deviation of 0.8 years.
Step 2 of 2: If a sampling distribution is created using samples of the ages at which 38 children begin reading, what would be the standard deviation of the sampling distribution of sample means? Round to two decimal places, if necessary.
Answers
Answer:
Step-by-step explanation:
The standard deviation of the sampling distribution of sample means is given by the formula:
standard deviation = population standard deviation / sqrt(sample size)
Here, the population standard deviation is 0.8 years, and the sample size is 38. Substituting these values into the formula, we get:
standard deviation = 0.8 / sqrt(38)
standard deviation ≈ 0.13
Rounding to two decimal places, the standard deviation of the sampling distribution of sample means is approximately 0.13 years.
Find the derivative of f(x) = -2x^3 by the limit process…

Answers
Answer:
f'(x) = -6x^2
f'(-5) = -150
f'(0) = 0
f'(√17) = -102
Arrange the expressions below in order from least to greatest. Place the least at the top and greatest at the bottom. ( 72 ÷ 8 ) − 2 × 3 + 1 72 ÷ ( 8 − 2 ) × 3 + 1 72 ÷ ( 8 − 2 ) × ( 3 + 1 ) 72 ÷ 8 − 2 × ( 3 + 1 )
Answers
Answer:
Step-by-step explanation:
2 × 3 + 1 72 ÷ ( 8 − 2 ) × 3 + 1 72 ÷ ( 8 − 2 ) × ( 3 + 1 ) 72 ÷ 8 − 2 × ( 3 + 1 )
Answer:
(72 divided by 8) second one, 72 divided by (8 - 2),third one, 72 divided by (8 - 2) x (3 + 1). last one. then the leftover number is the first one.
Step-by-step explanation:
Calculate
a) 20% of £150
b) 15% of 80 kg
c) 85% of 2500 m
Answers
Answer:
A) 30
B) 12 kg
C) 2,125 m
Step-by-step explanation:
Let i be the imaginary number √-1. Determine whether the expression a+bi, where a and b are real numbers, represents a real number or a non-real complex number for each case below. Select Real Number or Non-Real Complex number for each case.

Answers
Case 1: a = 0; b = 0 --> Real Number
Case 2: a = 0; b ≠ 0 --> Non-Real Complex Number
Case 3: a ≠ 0; b = 0 --> Real Number
Case 4: a ≠ 0; b ≠ 0 --> Non-Real Complex Number
Understanding Complex NumberFor each case, we can determine whether the expression a + bi represents a real number or a non-real complex number based on the values of a and b.
Case 1: a = 0; b = 0
In this case, both a and b are zero. The expression a + bi simplifies to 0 + 0i, which is equal to 0. Therefore, the expression represents a real number.
Case 2: a = 0; b ≠ 0
Here, a is zero, but b is nonzero. The expression a + bi becomes 0 + bi, where b is a nonzero real number multiplied by the imaginary unit i. Since the expression contains a nonzero imaginary part, it represents a non-real complex number.
Case 3: a ≠ 0; b = 0
In this case, a is nonzero, but b is zero. The expression a + bi simplifies to a + 0i, which is equal to a. As there is no imaginary part in the expression, it represents a real number.
Case 4: a ≠ 0; b ≠ 0
Here, both a and b are nonzero. The expression a + bi contains both a real part (a) and an imaginary part (bi). Thus, it represents a non-real complex number.
Learn more about complex number here:
https://brainly.com/question/5564133
#SPJ1

Terri buys five and seven-eighths ounces of chocolate chips. She uses four and four-sixths ounces in a recipe. How many ounces of chocolate chips does she have left?
Answers
Answer:
1 5/24 ounces--------------------------
Find the difference of the initial and used amounts:
5 7/8 - 4 4/6 = 5 - 4 + 7/8 - 4/6 = Combine whole and fraction parts1 + 7/8 - 2/3 = Simplify1 + 21/24 - 16/24 = Common denominator is 241 + 5/24 = Convert to mixed fraction1 5/24VERY EASY, WILL GIVE 50 POINTS FOR CORRECT ANSWER ASAP AND WILL GIVE BRAINLIEST.

Answers
Answer:
last choice
Step-by-step explanation:
trust me
Answer:
Go for the fourth option.
NEED HELP!! I"LL GIVE YOU BRAINLIEST!! Find the value of b. a = 3 and c =12

Answers
Answer: b = 11.62
Step-by-step explanation:
We can use this formula to solve for b:
\(b^{2} =\) \(\sqrt{c^{2}-a^{2} }\)
\(b^{2} =\) \(\sqrt{12^{2}-3^2 }\)
\(b^2= \sqrt{144-9}\)
= 11.61895004
We can round that to 11.62.
Hope this helped!
Tim is placing bricks in a bucket. The
bucket weighs 3 pounds and each brick
weighs 2 pounds. How many bricks, b, has
Tim placed in the bucket when the total
weight is 15 pounds?
Answers
Answer:
6
Step-by-step explanation:
15-3=12
12/2=6
you have to take away 3 for the bucket then you are left with 12 being from the bricks so you divide by 2 ending with 6 bricks being in the bucket
prove or provide a counter example of the following statement: if a and b are similar matrices and v is an eigenvector of a, then v is also an eigenvector of b.
Answers
If A and B are similar matrices and v is an eigenvector of A, then v is also an eigenvector of B , similarly if u is an eigenvector of B then u is also eigenvector of A.
Suppose A and B are n×n matrices over R or C. We say A and B are similar, or that A is similar to B, if there exists a matrix P such that B =P⁻¹AP.
The eigenvalues are the roots of the
characteristic polynomial.
B =P⁻¹AP ⇔ PBP⁻¹ = A
If Av = λv , then PBP⁻¹v = λv ⇒ BP⁻¹v = P⁻¹λv
So, if v is an eigenvector of A, with eigenvalue λ, then P⁻¹v (which is non-zero since P is invertible) is an eigenvector of B with the same eigenvalue. If u is an eigenvector for B then P⁻¹v is an eigenvector for A. So, every eigenvalue of A is an eigenvalue of B and since you can interchange the roles of A and B in the previous calculations, every eigenvalue of B is an eigenvalue of A too. Hence, A and B have the same eigenvalues.
To learn more about Eigenvector and eigen values, refer:
https://brainly.com/question/14406572
#SPJ4
Help asap!!!!!!
A.
B.
C.
D.
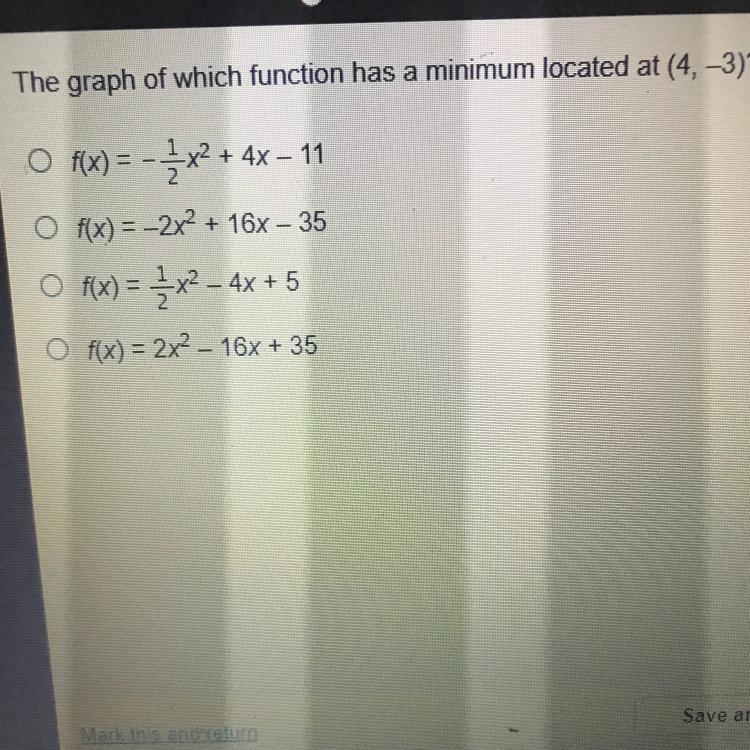
Answers
Answer:
Function has a minimum value
So, f(x)=0 and f(4)=-3
f(x)= - 1/2x^2+4x-11f(4)=-3 and f(x)=-x+4
f(4)=0
OAmalOHopeO
