Why might you need to use the addition or subtraction property of equality more than once after you have used the distributive property and combined like terms?
Answers
Answer:
If there is a variable term and a constant on each side of the equation, then you will need to use the addition or subtraction property of equality once to isolate the variable term and once to isolate the constant.
Related Questions
A recipe that serves 8 people requires 4 1/2 cup of flour how much do you need to serve for 24 people
Answers
Answer:
You would need thirteen and a half( \(13\frac{1}{2}\)) cups of flour.
Step-by-step explanation:
You can find this by taking \(4\frac{1}{2}\) and multiplying it by 3, since 24/8=3. This gives you \(13\frac{1}{2}\) .
May I please have the answers to this problem

Answers
Answer:
6x+5
Step-by-step explanation:
2x+4x =6x
10-5=5
6x+5
Tim predicts he will get 98 points on the next exam. If Tim actually earned 62 points, what was Tim's percent error?
Answers
Answer:
If Tim actually earned 62 points . Therefore Tim's percent error is 58.1 % .
Step-by-step explanation:
Carson and his children went into a restaurant where they sell hamburgers for $6 each and tacos for $2.50 each. Carson has $65 to spend and must buy a minimum of 12 hamburgers and tacos altogether. If Carson decided to buy 8 tacos, determine the maximum number of hamburger that he could buy.
Answers
Help plz ;~; this is so hard

Answers
Answer:
x = 29.15
Step-by-step explanation:
a^2 + b^2 = c^2
15^2 + 25^2 = 890
square root of 850 is 29.154759....
:)
Answer:
The correct answer is 30.
Step-by-step explanation:
To find this out I found the fraction of 6 and 8 to 10. This is 3/5 and 4/5 to find x on the other triangle all I had to do was multiply 25 times 1 1/5. Sorry for the bad explanation it was kind of confusing to word but I hope this helps!
8t – 13t + 10 (t – 2) = 34
Answers
Answer:
t=10.9
Step-by-step explanation:
8t-13t+10(t-2)=34
8t-13t+10t-20=34
5t-20=34
5t=54
t=10.9
As the CAPS document outlines, the Content Specification and Content Clarification for Patterns, Functions, and Algebra shows sequenced mathematics content topics and a content area spread. In the Intermediate Phase, select one topic and report on the topic sequence and content area spread. Your report should demonstrate mathematics concepts and procedures’ hierarchical and logical progression.
Answers
Answer:
Step-by-step explanation:
In the Intermediate Phase of mathematics education, one topic that demonstrates a hierarchical and logical progression in patterns, functions, and algebra is the concept of "Linear Equations."
The topic of Linear Equations in the Intermediate Phase builds upon the foundation laid in earlier grades and serves as a stepping stone towards more advanced algebraic concepts. Here is an overview of the topic sequence and content area spread for Linear Equations:
Introduction to Variables and Expressions:
Students are introduced to the concept of variables and expressions, learning to represent unknown quantities using letters or symbols. They understand the difference between constants and variables and learn to evaluate expressions.
Solving One-Step Equations:
Students learn how to solve simple one-step equations involving addition, subtraction, multiplication, and division. They develop the skills to isolate the variable and find its value.
Solving Two-Step Equations:
Building upon the previous knowledge, students progress to solving two-step equations. They learn to perform multiple operations to isolate the variable and find its value.
Writing and Graphing Linear Equations:
Students explore the relationship between variables and learn to write linear equations in slope-intercept form (y = mx + b). They understand the meaning of slope and y-intercept and how they relate to the graph of a line.
Systems of Linear Equations:
Students are introduced to the concept of systems of linear equations, where multiple equations are solved simultaneously. They learn various methods such as substitution, elimination, and graphing to find the solution to the system.
Word Problems and Applications:
Students apply their understanding of linear equations to solve real-life word problems and situations. They learn to translate verbal descriptions into algebraic equations and solve them to find the unknown quantities.
The content area spread for Linear Equations includes concepts such as variables, expressions, equations, operations, graphing, slope, y-intercept, systems, and real-world applications. The progression from simple one-step equations to more complex systems of equations reflects a logical sequence that builds upon prior knowledge and skills.
By following this hierarchical progression, students develop a solid foundation in algebraic thinking and problem-solving skills. They learn to apply mathematical concepts and procedures in a systematic and logical manner, paving the way for further exploration of patterns, functions, and advanced algebraic topics in later phases of mathematics education.
Evaluate sin 60° without using a calculator by using ratios in a reference triangle.
Answers
PLEASE HELP IF U CAN!

Answers
Answer:
\(x = 8\)
Step-by-step explanation:
Given
The attached triangle
Required
Determine the value of x
x represents the height of the triangle.
And the area of a triangle is calculated as:
\(Area = \frac{1}{2} * Base * Height\)
Where
\(Base = 4\)
\(Area = 16\)
\(Height = x\)
The expression becomes
\(16 = \frac{1}{2} * 4* x\)
\(16 = 2* x\)
\(16 = 2x\)
Divide through by 2
\(8 = x\)
\(x = 8\)
Write an equation for a rational function with the given characteristic.
Vertical asymptotes at x = -2 and x = 3, x-intercepts at (-4,0) and (-1,0), y-intercepts at (0,4)
f(x) =
Answers
The rational function with the given characteristics is:
f(x) = -6(x + 4)*(x + 1)/[(x - 2)*(x + 3)]
How to write the rational function?We want to write a rational function with the given characteristics, first we want to have vertical asymptotes at x = -2 and x = 3, then the denominator must be:
(x - 2)*(x + 3)
We also want to have x-intercepts at (-4,0) and (-1,0), this means that the numerator must be:
a*(x + 4)*(x + 1)
Where a is a real number, then the rational function is:
f(x) = a*(x + 4)*(x + 1)/[(x - 2)*(x + 3)]
Now we want to have an y-intercept at (0, 4)
Then we must have:
f(0) = 4 = a*(0 + 4)*(0 + 1)/[(0 - 2)*(0+ 3)]
4 = a*4/-6
(-6/4)*4 = a
-6 = a
The rational function is:
f(x) = -6(x + 4)*(x + 1)/[(x - 2)*(x + 3)]
Laern more about rational functions at:
https://brainly.com/question/1851758
#SPJ1
For #10 – 12, use the diagram to the right.
10)
m 2 =
11)
m2 3 =
419
2
3
4
12)
m2 4=

Answers
Answer:
What is the value of x in the product of powers below?
6 Superscript 9 times 6 Superscript x = 6 squared
Negative 11
negative 7
7
11
Step-by-step explanation:
SOMEBODY HELP MATH 100 POINTS BRAINLIEST⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️ HELP MATH 100 POINTS BRAINLIEST ⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️HELP MATH 100 POINTS BRAINLIESTHELP MATH 100 POINTS BRAINLIEST⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️ HELP MATH 100 POINTS BRAINLIEST ⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️HELP MATH 100 POINTS BRAINLIESTHELP MATH 100 POINTS BRAINLIEST⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️ HELP MATH 100 POINTS BRAINLIEST ⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️HELP MATH 100 POINTS BRAINLIEST
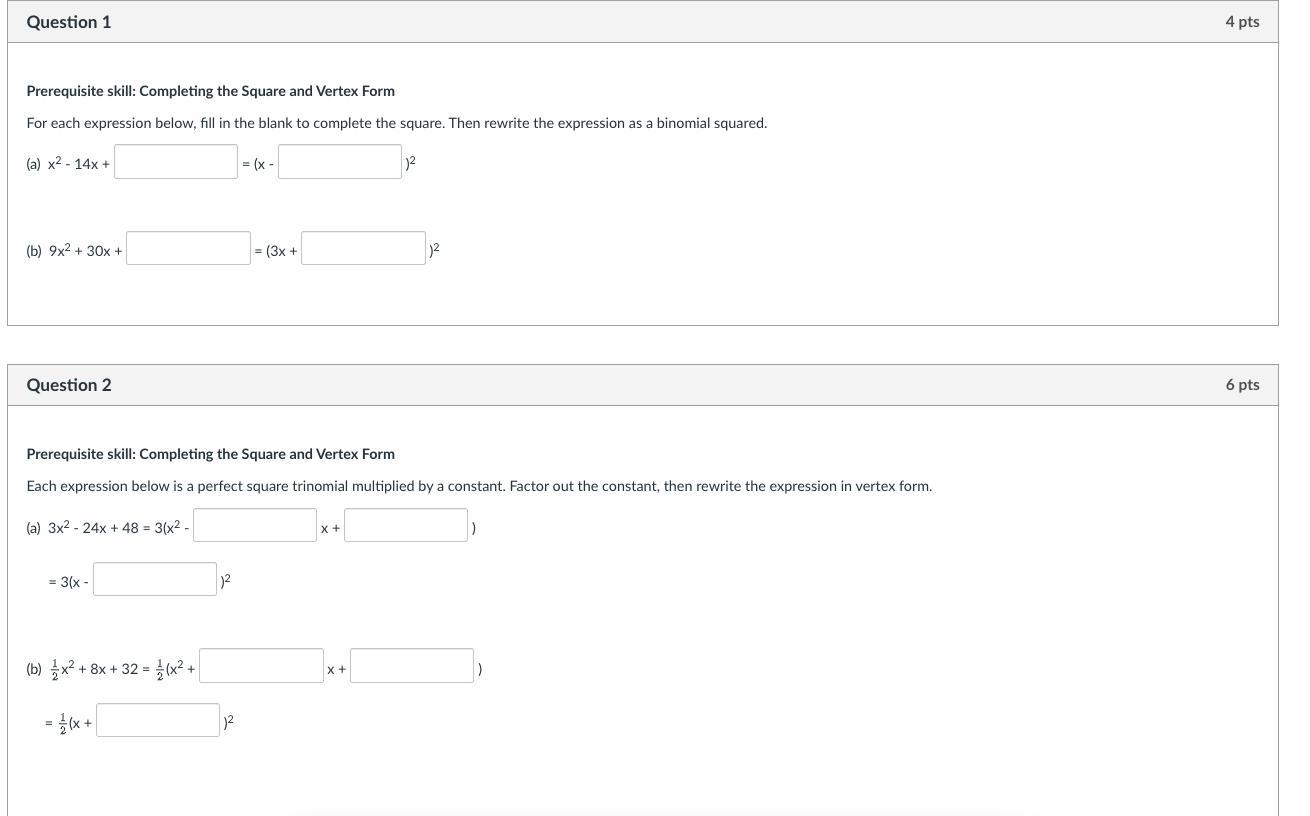
Answers
Answer:
\(\textsf{1.(a)} \quad x^2-14x+\boxed{49}=\left(x-\boxed{7}\right)^2\)
\(\textsf{1.(b)} \quad 9x^2 + 30x +\boxed{25}= \left(3x +\boxed{5}\right)^2\)
\(\begin{aligned}\textsf{2.(a)}\quad3x^2-24x+48&=3\left(x^2-\boxed{8}\:x+\boxed{16}\right)\\&=3\left(x-\boxed{4}\right)^2\end{aligned}\)
\(\begin{aligned}\textsf{2.(b)}\quad \dfrac{1}{2}x^2+8x+32&=\dfrac{1}{2}\left(x^2+\boxed{16}\:x+\boxed{64}\right)\\&=\dfrac{1}{2}\left(x+\boxed{8}\right)^2\end{aligned}\)
Step-by-step explanation:
Question 1(a) When completing the square for a quadratic equation in the form ax² + bx + c where the leading coefficient is one, we need to add the square of half the coefficient of the x-term:
\(x^2-14x+\left(\dfrac{-14}{2}\right)^2\)
\(x^2-14x+\left(-7\right)^2\)
\(x^2-14x+49\)
We have now created a perfect square trinomial in the form a² - 2ab + b². To factor a perfect square trinomial, use the following formula:
\(\boxed{a^2 -2ab + b^2 = (a -b)^2}\)
Therefore:
\(a^2=x^2 \implies a=1\)
\(b^2=49=7^2\implies b = 7\)
Therefore, the perfect square trinomial rewritten as a binomial squared is:
\(x^2-14x+\boxed{49}=\left(x-\boxed{7}\right)^2\)
(b) When completing the square for a quadratic equation where the leading coefficient is not one, we need to add the square of the coefficient of the x-term once it is halved and divided by the leading coefficient, and then multiply it by the leading coefficient:
\(9x^2 + 30x +9\left(\dfrac{30}{2 \cdot 9}\right)^2\)
\(9x^2 + 30x +9\left(\dfrac{5}{3}\right)^2\)
\(9x^2 + 30x +9 \cdot \dfrac{25}{9}\)
\(9x^2 + 30x +25\)
We have now created a perfect square trinomial in the form a² + 2ab + b². To factor a perfect square trinomial, use the following formula:
\(\boxed{a^2 +2ab + b^2 = (a +b)^2}\)
Therefore:
\(a^2=9x^2 = (3x)^2 \implies a = 3x\)
\(b^2=25 = 5^2 \implies b = 5\)
Therefore, the perfect square trinomial rewritten as a binomial squared is:
\(9x^2 + 30x +\boxed{25}= \left(3x +\boxed{5}\right)^2\)
\(\hrulefill\)
Question 2(a) Factor out the leading coefficient 3 from the given expression:
\(3x^2-24x+48=3\left(x^2-\boxed{8}\:x+\boxed{16}\right)\)
We have now created a perfect square trinomial in the form a² - 2ab + b² inside the parentheses. To factor a perfect square trinomial, use the following formula:
\(\boxed{a^2 -2ab + b^2 = (a -b)^2}\)
Factor the perfect square trinomial inside the parentheses:
\(=3\left(x-\boxed{4}\right)^2\)
(a) Factor out the leading coefficient 1/2 from the given expression:
\(\dfrac{1}{2}x^2+8x+32=\dfrac{1}{2}\left(x^2+\boxed{16}\:x+\boxed{64}\right)\)
We have now created a perfect square trinomial in the form a² + 2ab + b² inside the parentheses. To factor a perfect square trinomial, use the following formula:
\(\boxed{a^2+2ab + b^2 = (a +b)^2}\)
Factor the perfect square trinomial inside the parentheses:
\(=\dfrac{1}{2}\left(x+\boxed{8}\right)^2\)
Step-by-step explanation:
Since ABCD is a rectangle
⇒ AB = CD and BC = AD
x + y = 30 …………….. (i)
x – y = 14 ……………. (ii)
(i) + (ii) ⇒ 2x = 44
⇒ x = 22
Plug in x = 22 in (i)
⇒ 22 + y = 30
⇒ y = 8
40% of drivers surveyed were driving between 60 to 70 mph.
There are double the amount of cars driving between 40 to 50 mph than driving 60 to 70 mph.
12% of drivers are between 70 to 80 mph
2 out of 5 cars are driving between 60 to 70 mph.

Answers
The required answer is the number of drivers between 40 and 50 is 4, the number of drivers between 50 and 60 is 8, the number of drivers between 60 and 70 is 10 and the number of drivers between 70 and 80 is 3.
Given that total number of driver driving the vehicle is 25.
40% of drivers surveyed were driving between 60 and 70 mph.
12% of drivers are between 70 and 80 mph.
The amounts of cars driving between 50 and 60 mph is double than amounts of cars driving between 40 and 50 mph .
The number of drivers who are driving between 60 and 70 mph is
40% of total numbers of drivers = 40/100 × 25 = 10 drivers.
The number of drivers who are driving between 70 and 80 mph is
12% of total numbers of drivers = 12/100 × 25 = 3 drivers.
The remaining number of drivers is the difference between total number of driver and sum of number of drivers between 60 and 70 and number of drivers between 70 and 80 is 25 - (10+3) =25 - 13 = 12.
Suppose the number of drivers between 40 and 50 be y then amounts of cars driving between 50 and 60 mph is 2y. The sum of drivers between 40 and 60 is 12.
That implies, y + 2y = 12.
Thus, 3y = 12.
Therefore, y = 4.
Hence, the number of drivers between 40 and 50 is 4, the number of drivers between 50 and 60 is 8, the number of drivers between 60 and 70 is 10 and the number of drivers between 70 and 80 is 3.
Learn more about frequency table click here:
https://brainly.com/question/29084532
#SPJ1
if the smallest of three consecutive numbers is odd is the sum of three numbers even or odd
Answers
Answer:
it might be both
Step-by-step explanation:
Find the value of p.
-25 = -4p + 19
Answers
4p= 19+25
2. Add 19 and 25
4p= 44
3. Divide by 4
p= 11
Answer:
9.75
Step-by-step explanation:
-25 = -4p + 19
-25 - 19 = -4p
-39 ÷ -4 = p
9.75 = p
Please help with this math question!

Answers
Answer:
5. Proofs attached to answer
Step-by-step explanation:
Proofs attached to answer

HELP ME ANSWER THIS QUESTIONS PLEASE

Answers
Answer:
5th horizontal line on the graph
Step-by-step explanation:
Use inductive reasoning to predict the most probable next number in the list.
3, 9, -3, 3, -9, -3, -15, -9, -21, ?
Need Help
Answers
Answer: -27
Step-by-step explanation: Use inductive reasoning to predict the most probable next number in the list.
3, 9, -3, 3, -9, -3, -15, -9, -21, ?
We can start by looking at the differences between consecutive terms in the list:
9 - 3 = 6 -3 - 9 = -12 3 - (-3) = 6 -9 - 3 = -12 -3 - (-9) = 6 -15 - (-3) = -12 -9 - (-15) = 6 -21 - (-9) = -12
Notice that the differences alternate between positive 6 and negative 12. This suggests that the pattern involves adding 6, then subtracting 12, and then adding 6 again. Applying this pattern to the last term in the list (-21), we get:
-21 + 6 = -15 -15 - 12 = -27 -27 + 6 = -21
Therefore, we predict that the most probable next number in the list is -27.
the equation a=0.003x^2+21.3 models the average ages of women when they first married since the year 1940. In this equation, a represents the average age and x represents the years since 1940. Estimate the year in which the average age of brides was the youngest
Answers
Answer:
Please help me important question in image
Step-by-step explanation:Please help me important question in image
Please help me important quePlease help me important question in image
stion in image
Please help me important question in image
Please help me important question in image
Answer:
The equation a=0.003x^2+21.3 models the average ages of women when they first married since the year 1940 in the United States. In this equation, a represents the average age and x represents the years since 1940. To estimate the year in which the average age of brides was the youngest, we need to find the minimum value of the quadratic function a=0.003x^2+21.3. This can be done by using the formula x=-b/2a, where b is the coefficient of x and a is the coefficient of x^2. In this case, b=0 and a=0.003, so x=-0/(2*0.003)=0. This means that the average age of brides was the lowest when x=0, which corresponds to the year 1940. The value of a when x=0 is a=0.003*0^2+21.3=21.3, so the average age of brides in 1940 was 21.3 years old. This is consistent with the historical data, which shows that the median age of women at their first wedding in 1940 was 21.5 years old. The average age of brides has been increasing since then, reaching 28.6 years old in 2021.
MARK AS BRAINLIEST!!!
Can someone help with this please?

Answers
Answer:
1 is linear, 2 is linear, 3 is not linear, 4 is not linear
Answer:
Function 1 is linear
Function 2 is linear
Function 3 is not linear
Function 4 is not linear
Determine all minors and cofactors of the matrix A given below (5)
2 −1 1 3
0 1 1 3
2 1 1 0
2 0 −1 −2
Answers
A minor of a matrix A is the determinant of some smaller square matrix, cut down from A by removing one or more of its rows and columns.
E.g the minor for a_11 is the matrix
1 1 3
1 1 0
0 -1 -2
The cofactor of an element is the minor but a factor, with that factor being (-1)^(i+j) where i and j are the row and column of the element
A cylinder has a radius of 4 millimeters. Its volume is 200.96 cubic millimeters. What is the height of the cylinder?
Answers
Answer:
3.999 millimeters.
Step-by-step explanation:
To find the height of the cylinder, we can use the formula for the volume of a cylinder:
V = πr²h
Given that the radius (r) of the cylinder is 4 millimeters and the volume (V) is 200.96 cubic millimeters, we can substitute these values into the formula and solve for the height (h).
200.96 = π(4²)h
200.96 = 16πh
To solve for h, we can divide both sides of the equation by 16π:
200.96 / (16π) = h
Using a calculator, we can calculate the approximate value of h:
h ≈ 200.96 / (16 × 3.14159)
h ≈ 3.999
Therefore, the height of the cylinder is approximately 3.999 millimeters.
Fred is standing at a point looking north. He walks on a bearing 056° for 9.8km before stopping. He then walks an additional 3.5 km on a bearing of 112° before stopping to rest. (a) Find out how far he is away from his start point using sine or cosine rule (b) Determine the area of the enclosed shape (c) Draw neat labeled scale diagram of the same
Answers
The area of the enclosed shape is about 14.47 km^2.
We are given that;
056° for 9.8km and 3.5 km on a bearing of 112°
Now,
We can see that the enclosed shape is a triangle with sides 9.8 km, 3.5 km, and z km, and angles 56°, 112°, and y°. We can use the fact that the sum of angles in a triangle is 180° to find y:
y = 180° - 56° - 112°
y = 12°
Now we can use the cosine rule to find z:
z^2 = 9.8^2 + 3.5^2 - 2(9.8)(3.5)cos(12°)
z^2 ≈ 101.87
z ≈ 10.09
Therefore, Fred is about 10.09 km away from his start point.
To find the area of the enclosed triangle, we can use the sine rule to find x, the height of the triangle:
sin(56°) = x/9.8
x = 9.8 sin(56°)
x ≈ 8.27
The area of a triangle is given by half the base times the height, so:
A = (1/2)(3.5)(8.27)
A ≈ 14.47
Therefore, by trigonometric ratios the answer will be 14.47 km^2.
Learn more about trigonometric;
https://brainly.com/question/21286835
#SPJ1
I need help with number 2...

Answers
For isosceles triangle RST the measure of angle T is 34 degree
In this question, we have been given a isosceles triangle RST with RS = RT.
So, by isosceles triangle theorem,
angle S = angle T
So, angle T = (3x - 2)°
We know that the sum of all angles of triangle is 180°
∠R + ∠S + ∠T = 180°
9x + 4 + 3x - 2 + 3x - 2 = 180°
15x + 4 - 4 = 180°
15x = 180°
x = 12
So, 3x - 2 = 3(12) - 2
= 34°
Therefore, for triangle RST the measure of angle T is 34 degree
Learn more about isosceles triangle here:
https://brainly.com/question/2456591
#SPJ1
A=B+C+D Solve the question for b?
Answers
Answer:
A = B + C + D
rearrange the equation
B = A - C - D
Step-by-step explanation:
rearrange the equation so B is on one side of the equal sign
A = B + C + D
A - C - D = B
Answer: B=A-C-D
Step-by-step explanation:
To solve for B, we want to use our algebraic variables to isolate B.
A=B+C+D [subtract both sides by C]
A-C=B+D [subtract both sides by D]
A-C-D=B
B=A-C-D
3. A new restaurant has been open for 6 days. The owner is tracking the number of customers served for these 6 days (day 1, 2, 3, 5, and 6). She determines the least regression equation estimating the number of customers on a given day is y = 1.03x + 229.4. If thus far the restaurant has been making a net profit of $5.82, on average per customer, which of the following statements is correct? OA. On day 7, the owner can expect 15 more customers than she has served on day 6. B. If the number of customers continues to follow the current trend, the restaurant will make a net profit of $1,377 on day 7. C. On day 12, the owner can expect a net profit of $1,300. D. Net profit for days 6 and 7 combined is expected to be less than the earned net profit on day 1.
Answers
In conclusion, none of the given statements are correct based on the information provided.
To determine the correct statement, let's analyze the given information and the regression equation:
The regression equation for estimating the number of customers on a given day is y = 1.03x + 229.4, where x represents the day number and y represents the number of customers served.
We are also given that the restaurant has been making a net profit of $5.82, on average per customer:
Now let's evaluate each statement:
A. On day 7, the owner can expect 15 more customers than she has served on day 6.
To determine the number of customers on day 7, we substitute x = 7 into the regression equation:
y = 1.03(7) + 229.4 = 7.21 + 229.4 = 236.61
So, the number of customers on day 7 is approximately 237, which is not 15 more than the number of customers served on day 6.
Therefore, statement A is incorrect.
B. If the number of customers continues to follow the current trend, the restaurant will make a net profit of $1,377 on day 7.
To calculate the net profit on day 7, we need to multiply the average net profit per customer ($5.82) by the number of customers on day 7:
Net profit on day 7 = $5.82 \(\times\) 237 ≈ $1,379.34
So, statement B is incorrect as the net profit on day 7 is not expected to be $1,377.
C. On day 12, the owner can expect a net profit of $1,300.
Since the question only provides information about the number of customers served for the first 6 days, we cannot determine the net profit on day 12.
Therefore, statement C is incorrect.
D. Net profit for days 6 and 7 combined is expected to be less than the earned net profit on day 1.
To calculate the net profit for days 6 and 7 combined, we need to calculate the number of customers on both days using the regression equation and then multiply it by the average net profit per customer.
Let's substitute x = 6 into the regression equation:
y = 1.03(6) + 229.4 = 6.18 + 229.4 ≈ 235.58
Now, let's calculate the net profit for days 6 and 7 combined:
Net profit on days 6 and 7 = ($5.82 \(\times\) 235) + ($5.82 \(\times\) 237) ≈ $2,735.2
Comparing this to the earned net profit on day 1, we cannot determine if it is less or greater without the information provided.
Therefore, statement D is incorrect.
In conclusion, none of the given statements are correct based on the information provided.
For similar question on regression equation.
https://brainly.com/question/25987747
#SPJ8
The book fair is this week, and there's a special deal for teachers. For every 5 hardcover books a teacher buys, he or she can get 2 paperback books for free. Ms. Baldwin is buying 35 hardcover books for her classroom library.
How many paperback books will Ms. Baldwin get for free?
paperback books
Answers
Express the reoccurring decimal 0.56 as a fraction
Please see screenshot
Answers
Answer:
I have made it in pic hope it helps

Select the correct product of the exponential expression.
4^5
O A. 4.5
B. 4.4.4.4.4
C. 4.4.4.4.4.4.4
D. 4

Answers
Answer:
B(4.4.4.4.4)
Step-by-step explanation:
4^5 = 4*4*4*4*4
If the equation below is solved by graphing, which statement is true? log (6 x + 10) = log 1/2 x
Answers
The solution to the given expression is x = -20/11
What are logarithmic functions?
Logarithmic function are inverse of exponential functions. Given the equation below;
log (6 x + 10) = log 1/2 x
In order to determine the solution to the given logarithmic equation, we will first have to cancel the logarithm on both sides to have
6x + 10 = 1/2x
Collect the like terms
6x - 1/2x = 0 - 10
Find the LCD
12x-x/2 = -10
11x/2 = -10
Cross multiply
11x = -2 * 10
11x = -20
Divide both sides by 11
11x/11 = -20/11
x = -20/11
Hence the solution to the given expression is x = -20/11
Learn more on log functions and graph here: https://brainly.com/question/2086094
#SPJ1