Why is mathematical induction a valid proof technique? Put the following steps of a proof of such in the correct order.
Place these in the proper order. T
a. hen the set S of positive integers for which P(n) is false is nonempty. So by the well- ordering property, S has a least element m.
b. Since Plm – 1) = P(m) (by our supposition), P(m) is true. This contradicts the choice of m. Thus P(n) is true for each positive integer n.
c.To show that P(n) must be true for all positive integers n, assume there is at least one positive integer for which P(n) is false.
d. We know that m cannot be 1, because P(1) is true. Because m is positive and greater than 1, m - 1 is a positive integer.
e. Furthermore, because m - 1 is less than m, it is not in S, so P(m – 1) must be true.
f. Suppose we know that P(1) is true and the proposition P(k) → Plk + 1) is true for all positive integers k.
Answers
Mathematical induction is a valid proof technique because it involves showing that a statement is true for all positive integers by establishing a base case and a recursive step. The correct order is f, c, a, d, e, and b.
The steps of proof of mathematical induction in order are:
To show that P(n) must be true for all positive integers n, assume there is at least one positive integer for which P(n) is false.Then the set S of positive integers for which P(n) is false is nonempty. So by the well-ordering property, S has the least element m.We know that m cannot be 1, because P(1) is true. Because m is positive and greater than 1, m - 1 is a positive integer.Furthermore, because m - 1 is less than m, it is not in S, so P(m – 1) must be true.Since P(m – 1) = P(m) (by our supposition), P(m) is true. This contradicts the choice of m. Thus P(n) is true for each positive integer n.Suppose we know that P(1) is true and the proposition P(k) → Plk + 1) is true for all positive integers k.In summary, we first assume that P(1) is true and that P(k) → P(k + 1) is true for all positive integers k. Then, we assume that there exists at least one positive integer m for which P(m) is false and use the well-ordering property to find the smallest such integer. We then show that P(m-1) must be true, which contradicts the choice of m. Therefore, P(n) must be true for all positive integers n.
Therefore, mathematical induction is a valid proof technique and can be used to prove the truth of propositions for all positive integers.
To know more about "mathematical induction": https://brainly.com/question/29503103
#SPJ11
Related Questions
What is the slope of this equation?y= -1/2x −3 Question 2 options: 0 -3 -1/2
Answers
Answer:
-1/2
Step-by-step explanation:
In the equation y=mx+b..
y and x are the coordinates that go into your function
m is the slope
and b is the y intercept
looking at y=-1/2x-3 i can tell that -1/2 is in the place of m which is slope, and -3 is the y intercept.
Using simplex method to solve the following problems: (Manual calculations and then confirm your calculation by any software) Max. Z=5A+4B Subject to constraints: 6 A+4 B≤24, A+2 B≤6,−A+B≤1, B≤2, A, B≥0
Answers
Using the simplex method, the maximum value of Z=5A+4B is found to be 19.2 when A=3.6 and B=1.2. The calculations can be confirmed by using any software that solves linear programming problems.
To solve the given linear programming problem using the simplex method, we start by converting the problem into standard form. We introduce slack variables to convert the inequalities into equations.The initial tableau is as follows:
| A | B | S1 | S2 | S3 | S4 | RHS
------------------------------------------
Z | -5 | -4 | 0 | 0 | 0 | 0 | 0
------------------------------------------
S1 | 6 | 4 | 1 | 0 | 0 | 0 | 24
S2 | 1 | 2 | 0 | 1 | 0 | 0 | 6
S3 | -1 | 1 | 0 | 0 | 1 | 0 | 1
S4 | 0 | 1 | 0 | 0 | 0 | 1 | 2
We perform the simplex iterations until the optimal solution is reached. After applying the simplex method, the final tableau is obtained as follows:
| A | B | S1 | S2 | S3 | S4 | RHS
------------------------------------------------------
Z | 0 | 1.8 | 0.2 | -1 | -0.4 | 0.4 | 19.2
------------------------------------------------------
S1 | 0 | 0 | 0 | 1.5 | -1 | 1 | 3
S2 | 1 | 0 | -0.5 | 0.5 | 0.5 | -0.5 | 1.5
A | 1 | 0 | 0.5 | -0.5 | -0.5 | 0.5 | 0.5
S4 | 0 | 0 | 1 | -1 | -1 | 1 | 1
From the final tableau, we can see that the maximum value of Z is 19.2 when A=3.6 and B=1.2. This solution satisfies all the constraints of the problem. The calculations can be verified using any software that solves linear programming problems, which should yield the same optimal solution.
Learn more about linear programming here:- brainly.com/question/30763902
#SPJ11
(2x10^6) x (0.00009)
Answers
180
First, let's state what we are given:
\((2\text{ }\times10^6)\times(0.00009)\)Then we convert the decimal to standard form and solve:
\(\begin{gathered} 0.00009\text{ = 9}\times10^{-5}\text{ in standard form} \\ 2\text{ }\times10^{6\text{ }}\times9\times10^{-5} \\ =\text{ 2}\times9\text{ }\times10^{6-5} \\ =\text{ 18 }\times10^1\text{ = 18}\times10 \\ =\text{ 180} \end{gathered}\)(2x10^6) x (0.00009) = 180
help with this 10th grade geometry problem?

Answers
Answer:
3.5m
Step-by-step explanation:
Volume of pyramid = lwh÷3
25.77 = [(4.7)² × x] ÷ 3
25.77 × 3 = 22.09x
77.31 = 22.09x
x = 77.31 ÷ 22.09
= 3.49
= 3.5m
Find the ratio of the width of this basketball court to its perimeter. 5 feet (width) 117 feet (Oength) The ratio of the width of this basketball court to its perimeter isE Type the ratio as a simplified fraction.)
Answers
The ratio of the width of the basketball court to its perimeter is 5/244. This simplified fraction represents the relationship between the width and perimeter of the basketball court.
To find the perimeter of the basketball court, we add twice the width and twice the length. In this case, the width is 5 feet and the length is 117 feet. So the perimeter is 2 * (5 feet + 117 feet) = 244 feet.
Now, we can calculate the ratio by dividing the width by the perimeter:
Ratio = Width / Perimeter
= 5 feet / 244 feet
To simplify the fraction, we can divide both the numerator and denominator by their greatest common divisor (GCD). In this case, both 5 and 244 have a GCD of 1, so the ratio remains the same:
Ratio = 5 feet / 244 feet
Therefore, the ratio of the width of the basketball court to its perimeter is 5/244.
To learn more about Ratios, visit:
https://brainly.com/question/12024093
#SPJ11
length []=0
length (x:xs)=1+ length xs
−L1
−L2
Consider the following data types and functions: data Direction =L∣R numR : [Direction] -> Int
numR []=0
numR (L:p)= numR p
numR (R:p)=1+ numR p
−N0
−NL
−NR
rem :: Direction −> [Direction] −> [Direction] rem d [ = ] − Remo rem d(L:p)= ∣d==L= rem dp− RemL1 lotherwise =L:(remdp)− RemL2 rem d(R:p)= lotherwise = R:(rem d p) ⋯ RemR2 Notice how "rem L p" removes all occurrences of L in p. Similarly, "rem R p" removes all occurrences of R in p. Similarly, "rem R p" removes all occurrences of R in p. The goal of this question is to show that: length p= length ( rem Rp)+ numR p. Answer the following questions: 1. What precisely should we prove by induction? Specifically, state a property P, including possible quantifiers, so that proving this property by induction implies the (above) goal of this exercise. 2. State (including possible quantifiers) and prove the base case goal. 3. State (including possible quantifiers) the inc्acuctive hypothesis of the proof. 4. State (including possible quantifiers) and prove the step case goal.
Answers
1) The property P that we need to prove by induction is as P(p) = length p = length (rem R p) + numR p. 2) For the base case, we need to prove P([]) = length [] = length (rem R []) + numR []. 3) Inductive hypothesis is P(p) = length p = length (rem R p) + numR p. 4) For the step case, we need to prove P(p) → P(L:p) : length (L:p) = length (rem R (L:p)) + numR (L:p).
1) The property P that we need to prove by induction is as follows:
For all lists of directions p, the property P(p) is defined as:
P(p) = length p = length (rem R p) + numR p
If we can prove this property P by induction, it implies the goal of the exercise, which is to show that length p = length (rem R p) + numR p.
2) Base case goal:
For the base case, we need to prove the following goal:
For an empty list of directions p = [], the property P(p) holds:
P([]) = length [] = length (rem R []) + numR []
Proof:
P([]) simplifies to:
length [] = length (rem R []) + numR []
Using the definition of the length function and rem function, we have:
0 = length [] + numR []
Since the length of an empty list is 0, and there are no occurrences of R in an empty list, numR [] is also 0. Therefore, the base case goal holds.
3) Inductive hypothesis:
Assuming that the property P holds for a list p, we assume the following inductive hypothesis:
P(p) = length p = length (rem R p) + numR p
4) Step case goal:
For the step case, we need to prove the following goal:
Assuming P(p), we need to show that P(L:p) holds:
P(p) → P(L:p) : length (L:p) = length (rem R (L:p)) + numR (L:p)
Proof:
Using the definition of the length function and rem function, we have:
length (L:p) = length (L:(rem R p)) + numR (L:p)
Expanding the length and rem functions, we get:
1 + length p = 1 + length (rem R p) + numR (L:p)
Since L is not equal to R, numR (L:p) remains unchanged:
1 + length p = 1 + length (rem R p) + numR p
By canceling out the common terms on both sides, we get:
length p = length (rem R p) + numR p
This matches the property P(p), so the step case goal holds.
By proving the base case and the step case, we have proven the property P(p) by induction, which implies that length p = length (rem R p) + numR p for all lists of directions p.
Correct Question :
length []=0
length (x:xs)=1+ length xs
−L1
−L2
Consider the following data types and functions: data Direction =L∣R numR : [Direction] -> Int
numR []=0
numR (L:p)= numR p
numR (R:p)=1+ numR p
Answer the following questions:
1. What precisely should we prove by induction? Specifically, state a property P, including possible quantifiers, so that proving this property by induction implies the (above) goal of this exercise.
2. State (including possible quantifiers) and prove the base case goal.
3. State (including possible quantifiers) the inc्acuctive hypothesis of the proof.
4. State (including possible quantifiers) and prove the step case goal.
To learn more about induction here:
https://brainly.com/question/13079664
#SPJ4
Unit 2 logic and proof homework 3 conditional statements
Answers
By engaging in these exercises, students can develop a deeper understanding of conditional statements and logical reasoning, which are essential skills for further studies in mathematics and logic.
In Unit 2 of a logic and proof course, homework 3 focuses on conditional statements.
Conditional statements are fundamental concepts in logic and mathematics, representing logical implications between two statements.
They are typically expressed in "if-then" format, where the "if" part is the hypothesis and the "then" part is the conclusion.
The homework may involve tasks such as:
Identifying conditional statements: Students are given a set of statements and asked to identify which ones are conditional statements.
They need to recognize the "if-then" structure and correctly identify the hypothesis and conclusion.
Analyzing the truth value of conditional statements:
Students may be given conditional statements and asked to determine whether they are true or false.
They need to evaluate the hypothesis and conclusion to determine if the implication holds in each case.
Writing converse, inverse, and contrapositive statements:
Students may be required to manipulate given conditional statements to form their converse, inverse, and contrapositive statements.
This involves switching the positions of the hypothesis and conclusion or negating both parts.
Applying the laws of logic:
Students may need to apply logical laws, such as the Law of Detachment or the Law of Modus Tollens, to deduce conclusions based on conditional statements.
Constructing counterexamples:
Students may be asked to provide counterexamples to disprove statements that are falsely claimed to be universally true based on a given conditional statement.
They also help students develop critical thinking and problem-solving abilities, as they have to analyze and manipulate logical structures.
For similar questions on conditional
https://brainly.com/question/27839142
#SPJ8
What do you put on the X axis of an ogive?
Answers
The X-axis (horizontal axis) often represents a "class boundaries" of such an ogive, whereas the Y-axis (vertical axis) typically shows the frequency count.
Explain about the ogive graph?A sort of frequency polygon that displays cumulative frequencies is an ogive, often known as a cumulative frequency polygon.
In other words, the graph adds the cumulative percents from left to right.On an ogive graph, "class boundaries" are shown along the x-axis while cumulative frequency is shown on the y-axis. Comparable to a histogram, an ogive features a single point that indicates in which the top right corner of the rectangular would be located in place of rectangles. This type of graph is typically simpler to make from such a frequency table.Thus, The X-axis (horizontal axis) often represents a class boundaries being measured of such an ogive.
To know more about the ogive, here
https://brainly.com/question/2500839
#SPJ4
write a function in terms of $t$ that represents the situation. your starting annual salary of $35,000 increases by 4% each year.
Answers
In this problem, the starting annual salary is $35,000 and increases by 4% each year. The task is to write a function in terms of t that represents this situation.
Modeling salary growth over time is a common task in finance and economics.
Let's call the salary after t years s(t).
Then, the salary after t years can be represented by the following function: s(t) = 35,000 * (1 + 0.04t).
This function says that the starting salary of $35,000 is multiplied by (1 + 0.04t) to find the salary after t years.
The constant 0.04 represents the 4% increase each year.
For example, if t = 1, then the salary after 1 year would be $35,000 * (1 + 0.04 * 1) = $36,400, and if t = 2, then the salary after 2 years would be $35,000 * (1 + 0.04 * 2) = $37,888.
Learn more about function here brainly.com/question/12431044
#SPJ4
Assume the Ziders continue to grow in the same pattern. How old would a Zider be that had 73 hairs?
Answers
Number of hairs in day 1 , a = 5.
Every day number of hairs increases by , d = 4.
So, it is an Arithmetic Progression with first term a = 5 and common difference d = 4.
So, number of hair in nth days is given by :
\(a_n=a+(n-1)d\\\\a_n=5+(n-1)4\)
Let, after x days number of hairs are 73.
\(73=5+(x-1)4\\\\x-1=\dfrac{73-5}{4}\\\\x=18\ days\)
Therefore, Zider is 18 days old.
Hence, this is the required solution.
im running out of things to say

Answers
Answer:
i think its b
Step-by-step explanation:
What is 2/2-6*23 Please answer this question.
Answers
You are on a Ferris wheel that has a radius of 80 feet and the bottom of the wheel is 3 feet above the ground. The Ferris wheel starts when you get on at the bottom and rotates counter- clockwise and has a period of 2 minutes. Create a parametric function to model your location on the Ferris wheel at a given time.
Answers
The parametric function for your location on the Ferris wheel at any given time:
x(t) = 80 * sin(2π * (t/2))
y(t) = 80 * cos(2π * (t/2)) + 3
To create a parametric function that models your location on the Ferris wheel at a given time, we need to come up with equations that describe your horizontal and vertical positions as functions of time.
Let's start with the horizontal position. Since the Ferris wheel rotates counter-clockwise, we know that your position on the wheel will increase as time goes on. We can express this as:
x(t) = 80cos(2πt/120)
Here, t represents time in seconds, and the factor of 2π/120 ensures that the function completes one full cycle (i.e. one trip around the wheel) in 120 seconds, or 2 minutes. The cosine function gives us a smooth, periodic curve that oscillates between -80 and 80, corresponding to your position on either side of the wheel's center.
Next, let's consider your vertical position. We know that you start at a height of 3 feet above the ground, and as the wheel rotates, your height will vary sinusoidally over time. We can express this as:
y(t) = 80sin(2πt/120) + 3
Here, the sine function gives us a smooth, periodic curve that oscillates between 77 and 83 feet (i.e. the radius of the wheel plus or minus 3 feet).
So, putting it all together, our parametric function for your location on the Ferris wheel at a given time t is:
(r(t), θ(t)) = (80cos(2πt/120), 80sin(2πt/120) + 3)
Here, r(t) and θ(t) represent your radial distance from the center of the wheel and the angle you've rotated from the starting position, respectively. This parametric function describes a smooth, periodic curve that traces out your path on the Ferris wheel as it rotates counter-clockwise.
Given the information, we know the Ferris wheel has a radius of 80 feet, the bottom is 3 feet above the ground, it rotates counter-clockwise, and has a period of 2 minutes.
To create a parametric function, we need two equations, one for the x-coordinate (horizontal) and one for the y-coordinate (vertical). Let's denote the time variable as t, measured in minutes.
1. X-coordinate (horizontal position):
Since the Ferris wheel rotates counter-clockwise, we can use the following equation for the x-coordinate:
x(t) = 80 * sin(2π * (t/2))
2. Y-coordinate (vertical position):
To account for the bottom of the Ferris wheel being 3 feet above the ground, we need to add 3 to the vertical equation:
y(t) = 80 * cos(2π * (t/2)) + 3
Now, we have the parametric function for your location on the Ferris wheel at any given time:
x(t) = 80 * sin(2π * (t/2))
y(t) = 80 * cos(2π * (t/2)) + 3
Learn more about parametric function at: brainly.com/question/23725782
#SPJ11
iq scores in a certain population are normally distributed. it is given that: (1) 13% of people have iq that does not exceed 80. (2) mensa is an organization whose members have iqs in the top 3% of the population. the minimum iq score required for admission to mensa is 128. 9(a) find the mean and the standard deviation of iq scores. round your answers to the nearest whole numbers. hint. find z-scores.
Answers
The mean IQ score in the population is approximately 98, and the standard deviation is approximately 16.
Let μ = mean and σ = standard deviation of IQ scores in population.
Then we can write the two equations as :
⇒ P(X ≤ 80) = 0.13 ...equation(1)
⇒ P(X ≥ 128) = 0.03 ...equation(2)
we standardize the data by using the formula:
⇒ Z = (X - μ)/σ,
Where Z = standard normal variable.
Using the standard normal distribution, we know that P(Z ≤ -1.126) = 0.13,
So, -1.126 = (80 - μ)/σ .....equation(3),
and we know that P(Z ≥ 1.881) = 0.03.
So, 1.88 = (128 - μ)/σ ...equation(4),
⇒ μ = 128 - 1.881σ,
Solving equation(3) and equation(4),
We get,
⇒ σ ≈ 16.
Substituting σ = 16 into the equation(4),
We get,
⇒ μ = 128 - 1.881×16,
⇒ μ = 98.
Therefore, the mean IQ score = 98, and standard deviation is = 16.
Learn more about Standard Deviation here
https://brainly.com/question/30394343
#SPJ4
A circular grassy area of(172 square
feet is being watered by a sprinkler
set in the middle. How far does the
water spray from the sprinkler as it
rotates? Round your answer to the
nearest foot.
Answers
The distance the water sprays as the sprinkler rotates is 7.34 ft
Since the grassy area is circular, its area is the area of a circle.
Area of a circleSo, A = πr² where r = radius of circle = distance sprinkler sprays
The distance the water spraysMaking r subject of the formula, we have
r = √(A/π)
Since A = 172 ft², substituting the values of the variables into the equation, we have
r = √(A/π)
r = √(172 ft²/π)
r = √(172 ft²/3.142)
r = √(54.749 ft²)
r = 7.34 ft
So, the distance the water sprays as the sprinkler rotates is 7.34 ft
Learn more about area of a circle here:
https://brainly.com/question/12269818
If the process standard deviation is 0.5, and the sample size is 6, the standard deviation of the sample average is ___ .
Answers
For the given process, the standard deviation of the sample average is 0.2048.
A standard deviation (or σ) is a measure of how dispersed the data is in relation to the mean. Low standard deviation means data are clustered around the mean, and high standard deviation indicates data are more spread out. Given that process standard deviation is 0.5 and the sample size is 6. We are to find the standard deviation of the sample average. We know that the formula for standard deviation of sample means is given by:σx=σ/√nWhereσx is the standard deviation of the sample mean or average,σ is the standard deviation of the population and n is the sample size. So, σ = 0.5 and n = 6Now,σx=0.5/√6σx=0.2048 (rounded to 4 decimal places).Therefore, the standard deviation of the sample average is 0.2048.
Let's learn more standard deviation:
https://brainly.com/question/475676
#SPJ11
5+3 + 7 = 5 + 7 + 3 O A. True B. Fa
Answers
Answer:
its true
Step-by-step explanation:
a drawing class was assigned a final project where students had to choose one art medium and one genre. the professor kept track of the types of projects submitted. portrait landscape acrylic paint 3 4 oil paint 2 2 what is the probability that a randomly selected student used acrylic paint given that the student chose to create a portrait? simplify any fractions.
Answers
The probability that a randomly selected student used acrylic paint given that the student chose to create a portrait is 3/5 or 60%.
To find the probability that a randomly selected student used acrylic paint given that the student chose to create a portrait, you can use the conditional probability formula:
P(Acrylic Paint | Portrait) = P(Acrylic Paint and Portrait) / P(Portrait)
From the given data:
- There were 3 students who used acrylic paint and created a portrait.
- There were a total of 5 students who created a portrait (3 with acrylic paint and 2 with oil paint).
So, the probability calculation would be:
P(Acrylic Paint | Portrait) = (3/5) / (5/5) = 3/5
Learn more about conditional probability here: https://brainly.com/question/28339868
#SPJ11
The Gross revenue is $495,958.02. AR is 14% of the Gross RevenueWhat amount is tied up in AR?
Answers
The amount tied up in AR is $69434.12
Explanation:The Gross Revenue, GR = $495,958.02
From the question:
The Annual Revenue, AR = 14% of GR
AR = (14/100) x $495,958.02
AR = 0.14 x $495,958.02
AR = $69434.12
The amount tied up in AR is $69434.12
Simplify the answer

Answers
Answer:
11/12
Step-by-step explanation:
Answer:
A. 11/12 cup
Step-by-step explanation:
3 1/4 = 2 5/4
2 5/4-2 1/3 = 5/4-1/3
5/4-1/3 = 11/12
If Mike runs 3/5 of a mile in 1/15 of an hour, how many miles would he walk in a full hour?
Answers
Answer:
9 miles
Step-by-step explanation:
The answer is 9 miles because if you divide 0.6 mile by 4 minutes, you will have an answer of 9 miles an hour, as 0.6x15=9. In a full hour, Mike would walk 9 miles.
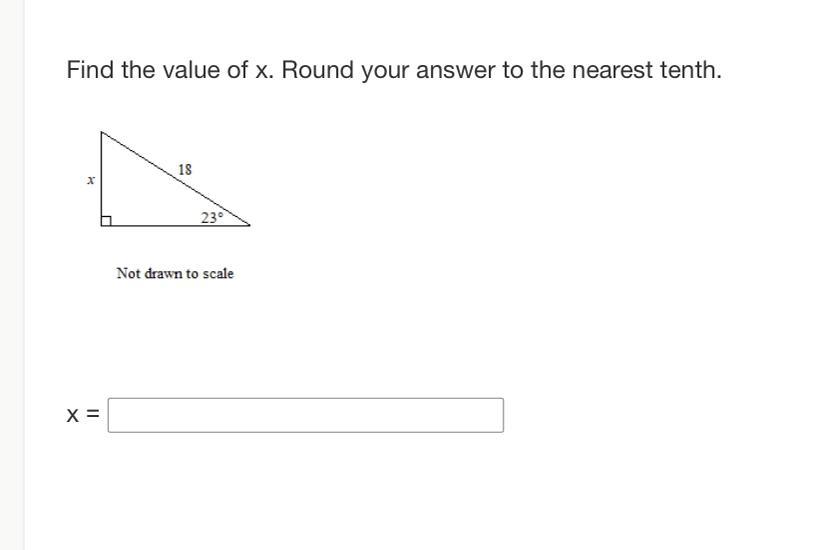
Solve for X (Trigonometry)
Answers
Answer:
7.0
Step-by-step explanation:
When doing trigonometry, remember SOH-CAH-TOA...
Sine : Opposite/Hypotenuse
Cosine : Adjacent/Hypotenuse
Tangent : Opposite/Adjacent
In this figure, we are given the measure of a 23° angle, and two sides that are opposite of the angle, and the hypotenuse.
This means we need to use sine:
\(sin(23)=\frac{x}{18}\)
Multiply both sides by 18:
\(18sin(23)=x\)
\(18(0.391)=x\\x=7.038\\x\approx7.0\)
Any mathematicians up for puzzle?

Answers
Answer:
Search it up
Step-by-step explanation:
its on tthe internet
a. 25 - 3x = 40, х =
Answers
Answer:
x=-5
Step-by-step explanation:
25-3x=40
-3x=40-25 (both side -25)
-3x=15 (both side divide by 3)
x=5
Suppose f(x) = - 3x² + 9x − 2. Compute the following:
A.) ƒ( − 2) + f(1) =
B.) ƒ( − 2) – ƒ(1) =
Answers
Step-by-step explanation:
\( f(x) = - 3 {x}^{2} + 9x - 2\)
A) f(-2) + f(1) = -32 + 4 = -28
B) f(-2) - f(1) = -32 - 4 = -36
The probability of an event happening is 5/9 . What are the odds in favor of the event happening?
Answers
The odds in favor of the event happening are 5 to 4.
We have,
To find the odds in favor of an event happening, we use the formula:
Odds in favor = Probability of the event happening / Probability of the event not happening
In this case,
The probability of the event happening is 5/9.
The probability of the event not happening is 1 - 5/9, which simplifies to 4/9. So the odds in favor of the event happening are:
Odds in favor
= 5/9 / 4/9
= 5/4
Therefore,
The odds in favor of the event happening are 5 to 4.
Learn more about probability here:
https://brainly.com/question/14099682
#SPJ1
like the z distribution, the tdf distribution is symmetric around 0, bell-shaped, and with tails that approach the horizontal axis and eventually cross it. group startstrue or false
Answers
False. The statement is incorrect. Unlike the z distribution, the t-distribution is not symmetric around 0, and its tails do not approach the horizontal axis and cross it.
The t-distribution is similar to the normal (z) distribution in the sense that it is bell-shaped. However, there are important differences. The t-distribution is not symmetric around 0 but is centered at 0. It has a shape that depends on its degrees of freedom (df). As the degrees of freedom increase, the t-distribution approaches the shape of the standard normal distribution (z-distribution).
The tails of the t-distribution are thicker than the tails of the z-distribution. The t-distribution has more probability in the tails, which means it has more extreme values compared to the z-distribution. As the degrees of freedom increase, the t-distribution approaches the normal distribution, and its tails become closer to the horizontal axis, but they do not cross it.
It's important to note that the shape and characteristics of the t-distribution are determined by the degrees of freedom. As the degrees of freedom increase, the t-distribution becomes more similar to the z-distribution. However, even with large degrees of freedom, the t-distribution will always have slightly thicker tails than the z-distribution.
know more about distribution :brainly.com/question/29332830
#SPJ11
Given the side lengths, determine whether the triangle is acute, obtuse, right, or not a triangle

Answers
Answer:
It is an Acute-Angled Triangle.
Step-by-step explanation:
if it helps don't forget to like and mark me sister
Answer:
Acute triangle to be specific it is an Acute scalene triangle
Step-by-step explanation:
I will pay Venmo someone 50 dollars if they answer all 25 of my geometry questions please I’m desperate I have pics of all the questions
Answers
Answer:
Q1. A
Q2.C
Q3.C
Q4.D
Q5.C
Q6.D
Q7.C
Q8.D
Q9. A
Q10.D
Q11.B
Q12.B
Q13.A
Q14.A
Q15.C
Q16.C
Q17.B
Q18.D
Q19.A
Q20.B
Q21. A
Q22.B
Q23.D
Q24.C
Q25. A
Step-by-step explanation:
Urgent please help. Amanda surveyed 20 juniors and seniors at delamar high school to find the number of hours per week they spend working at part-time jobs. Her results are shown below.
Look at picture

Answers
Answer:
The correct statement is (C).
Step-by-step explanation:
The data for the number of hours per week they spend working at part-time jobs by 20 juniors and seniors at Delmar high school is:
Juniors: 20, 10, 20, 10, 15, 0, 0, 10, 20, 15
Seniors: 20, 20, 10, 10, 0, 0, 0, 10, 0, 10
Compute the mean of both the data:
\(\mu_{J}=\frac{1}{n}\sum\limits^{n}_{i=1}{x_{iJ}}\)
\(=\frac{1}{10}\times [20+10+20+10+15+0+0+10+20+15]\\\\=\frac{120}{10}\\\\=12\)
\(\mu_{S}=\frac{1}{n}\sum\limits^{n}_{i=1}{x_{iS}}\)
\(=\frac{1}{10}\times [20+ 20+10+10+0+0+0+10+0+10]\\\\=\frac{80}{10}\\\\=8\)
Compute the range of both the data:
\(Range_{J}=Max._{J}-Min._{J}\)
\(=20-0\\=20\)
\(Range_{S}=Max._{S}-Min._{S}\)
\(=20-0\\=20\)
It can be seen that the range of both the data is same, i.e. 20.
Thus, the correct statement is (C).