why does a sample census with plots located along a transect often provide more accurate data than a sample with plots that are located randomly?
Answers
The reason why a sample census with plots located along a transect often provides more accurate data than a sample with randomly located plots is, because it allows for a systematic and structured sampling approach.
When plots are located along a transect, they are selected in a way that ensures they are evenly distributed across the study area. This method eliminates the potential bias that can occur when using random sampling, where plots can be clustered together or occur in areas that do not represent the entire population.
By selecting plots along a transect, we can capture a wider range of environmental conditions and variations across the study area. This helps to increase the representativeness of the sample, as it includes plots from different habitats or zones within the transect.
Additionally, using plots located along a transect allows for a standardized sampling protocol. This means that the same measurements or observations are taken at each plot, ensuring consistency and comparability of data. With random sampling, the measurements or observations might vary, leading to potential inconsistencies in the collected data.
To illustrate this, let's consider a study on plant biodiversity in a forest. If we randomly select plots, we might end up with most of the plots being located in areas with similar vegetation or plant communities, which could result in an underrepresentation of certain plant species. However, if we select plots along a transect, we can ensure that we cover a wider range of vegetation types, increasing the chances of capturing a more accurate representation of plant diversity in the forest.
Learn more about Sampling Theory: https://brainly.com/question/13219833
#SPJ11
Related Questions
Please answer! I’ll give you Brainliest

Answers
A)
The four small squares are all 3x3, so the perimeter is 3+3+3+3 = 12.
12 * 4 = 48
We can find the perimeter of the large diamond shape using the Pythagorean theorem, a^2 + b^2 = c^2
a = 4
b = 4
4^2 + 4^2 = c^2
16 + 16 = c^2
32 = c^2
c = 5.65685425
So the perimeter of the large diamond shape is
5.65685425+5.65685425+5.65685425+5.65685425 = 22.627417
48+22.6 = 70.6
B)
The areas of the small squares are 3x3 = 9
9 * 4 = 36
The area of the large diamond shape is
5.65685425 * 5.65685425 = 32
36 + 32 = 68
This expression gives the solutions to which quadratic equation?
A. 3x^2+4=x
B.x^2+4=3x
C.x^2+4=-3x
D.4x^2+3=x
E. 3x^2+4=-x

Answers
This expression gives the solutions to quadratic equationx^2+4=3x.
What is quadratic equation?A quadratic equation is an equation of the form ax^2 + bx + c = 0, where a, b, and c are constants and x is an unknown variable. It is most commonly used to solve for the unknown variable in terms of the given constants. The solutions to a quadratic equation can be found using the quadratic formula.
This equation is a quadratic equation, which is an equation that can be expressed in the form ax2 + bx + c = 0, where a, b and c are constants and x is an unknown variable. In this case, a = 1, b = 4 and c = 0, so the equation can be written as x2 + 4x = 0. Solving this equation gives the solutions x = 0 and x = -4.
To know more about quadratic equation click-
https://brainly.com/question/1214333
#SPJ1
The probability of choosing a diamond card from a standard pack of cards is 0. 25, what is the probability of choosing any other suit?
Answers
Using the probability of complementary events, it is found that there is a 0.75 probability of any other suit.
What is the probability of complementary events?When two events are complementary, the sum of their probabilities are 1.
In this problem, a diamond card and a card for any other suit are complementary events, hence the equation is:
0.25 + p = 1
p = 0.75.
Thus, there is a 0.75 probability of any other suit.
More can be learned about the probability of complementary events at https://brainly.com/question/25578621
A machine used to fill cans of Campbell’s tomato soup (low salt) has the following characteristics: µ = 12 ounces and s = .5 ounces.
a. Depict graphically the sampling distribution of all possible values of , where is the sample mean (point estimator) for 30 cans selected randomly by a quality control inspector.
b. What is the probability of selecting a sample of 36 cans with a sample mean greater than 12.2 ounces?
Answers
1. The x-axis represents the sample mean (\(\bar x\)), and the y-axis represents the probability density.
2. The probability represents the area under the standard normal curve to the right of z = 2.197.
What is probability?Probability is a way to gauge how likely something is to happen. Many things are difficult to forecast with absolute confidence. Using it, we can only make predictions about the likelihood of an event happening, or how likely it is.
a. To depict the sampling distribution of all possible values of the sample mean, we can use a probability distribution graph, specifically a normal distribution graph.
Given that the population mean (µ) is 12 ounces and the population standard deviation (s) is 0.5 ounces, and assuming that the sample size is sufficiently large (n = 30), we can use the Central Limit Theorem to approximate the sampling distribution of the sample mean as a normal distribution.
The mean of the sampling distribution (\(\mu_\bar x\)) will be the same as the population mean, which is 12 ounces.
The standard deviation of the sampling distribution (\(\sigma_\bar x\)) can be calculated using the formula \(\sigma_\bar x\) = s / √n, where s is the population standard deviation and n is the sample size. In this case, \(\sigma_\bar x\) = 0.5 / √30 ≈ 0.091 ounces.
Using these values, we can plot a normal distribution curve with the mean at 12 ounces and the standard deviation of 0.091 ounces. The x-axis represents the sample mean (\(\bar x\)), and the y-axis represents the probability density.
b. To find the probability of selecting a sample of 36 cans with a sample mean greater than 12.2 ounces, we need to calculate the area under the sampling distribution curve to the right of 12.2 ounces.
First, we need to standardize the value of 12.2 ounces using the formula z = (\(\bar x\) - \(\mu_\bar x\)) / \(\sigma_\bar x\), where \(\bar x\) is the given sample mean, \(\mu_\bar x\) is the mean of the sampling distribution, and \(\sigma_\bar x\) is the standard deviation of the sampling distribution.
In this case, \(\bar x\) = 12.2 ounces, \(\mu_\bar x\) = 12 ounces, and \(\sigma_\bar x\) = 0.091 ounces.
z = (12.2 - 12) / 0.091 ≈ 2.197
Now, we can find the probability using the standard normal distribution table or statistical software. The probability represents the area under the standard normal curve to the right of z = 2.197.
Learn more about probability on:
https://brainly.com/question/13604758
#SPJ4
Amir operates a large lobster boat. The operating cost for the boat is $2.250 each day. At the end of each day, he sells all his freshly caught lobster to either the local restaurant or the local grocery store with the following conditions: • The price per pound that the restaurant is willing to pay follows a triangular distribution with minimum value $1.50, maximum value $5.50, and likeliest value $3.50. • The price per pound that the grocery store is willing to pay is decreasing with more lobsters: $3.85 - 50.0005 * y, where y is the total lobster amount sold in pounds. • The amount of lobster that Amir catches in a single day follows a normal distribution with mean 1,500 pounds and standard deviation sqrt(12,500) pounds. • Amir decides to sell a fixed percentage of lobster to the local restaurant and the rest to local grocery stores. Using either math or simulation, can you help Amir determine what percentage he should choose in order to maximize his expected profit in the long run?
Answers
To optimize his long-term predicted profit percentage, he should select 20.567%.
What are an example and a percentage?Both decimal and fractional forms of the expression are acceptable.
Given, The boat's daily running expense is $2,250.
$1.50 is the minimal amount.
a maximum of $5.50
Most likely value is $3.50. Now, each day's conclusion.
More lobsters mean a lower price per pound which the grocery shop will accept ($3.85 - $0.0005). × y,
Amir's daily haul of lobster has a normally distributed with a mean of 1,500 pounds and a standard deviation of 12,500 pounds.
He should therefore select 20.567% to increase his anticipated profit in the long run.
To know more about percentage visit:
https://brainly.com/question/14695543
#SPJ4
Important Please Help!!!!!!

Answers
assume that you have conducted the initial (main) analysis of the data from a 2x3 design (i.e., it's a two-way design and factor 1 has two levels and factor 2 has three levels). assume, also, that you found that (a) the main effect of factor 1 is significant, (b) the main effect of factor 2 is not significant, and (c) the interaction is not significant. what do you need to do next? note: you really want to read this question carefully.
Answers
The key next step would be to continue analyzing the data in order to fully understand the main effect of factor 1 and any potential factors that may be impacting the outcome variable.
After conducting the initial analysis of the data from a 2x3 design and finding that the main effect of factor 1 is significant, the main effect of factor 2 is not significant, and the interaction is not significant, the next step would be to further explore the significant main effect of factor 1. This could involve examining the data more closely to determine the nature of the effect and conducting post-hoc analyses to identify any significant differences between the two levels of factor 1. Additionally, further analysis could be conducted to investigate any potential moderating variables or covariates that may be influencing the relationship between factor 1 and the outcome variable. It is important to note that although the interaction was not significant, it is still important to report and interpret its absence as it can provide valuable information about the relationships between the variables being studied.
Learn more about outcome here
https://brainly.com/question/25688842
#SPJ11
How much the average cost of homeowners insurance in tennessee?
Answers
The location of the property, its age and condition, the value of the house and its contents, and the coverage options that the homeowner chooses can all affect the typical cost of homeowners insurance in Tennessee.
The average cost of homeowners insurance in Tennessee can vary depending on several factors, including the location of the property, the age and condition of the home, the value of the home and its contents, and the coverage options selected by the homeowner.
According to recent data from the National Association of Insurance Commissioners (NAIC), the average annual premium for homeowners insurance in Tennessee in 2018 was 1,211. However, this is only an average, and actual premiums can vary significantly based on individual circumstances.
To get a more accurate estimate of the cost of homeowners insurance for a specific property in Tennessee, it is recommended to contact multiple insurance providers and obtain quotes based on the property's unique characteristics and the desired level of coverage.
for such more question on average cost
https://brainly.com/question/27819027
#SPJ4
Find the length of the third side. If necessary, round to the nearest tenth.
13
15
Answers
The length of the third side of the triangle is 2√14 units.
According to the question,
We have the following information:
Note that the complete question will be related to the right angled triangle with hypotenuse 15 units and perpendicular 13 units.
(More to know: Pythagoras theorem can only be used in right-angled triangle.)
We can use the Pythagoras theorem to find the base of the right-angled triangle.
Let's denote the base with b, perpendicular with p and hypotenuse with h.
\(b^{2} = h^{2}- p^{2}\)
\(b^{2} = 15^{2} -13^{2}\)
\(b^{2} }\) = 225-169
b = √56
b = 2√14 units
Hence, the length of the third side of the triangle is 2√14 units.
To know more about length of the third side here
https://brainly.com/question/7890975
#SPJ1
X^2 + 4x + y^2-6y= -4 find radius and center
Answers
To find the centre and radius of the equation x^2+4x+y^2+6y=-4, we need to complete the square for both x and y terms.
For the x terms:
x^2 + 4x = (x + 2)^2 - 4
For the y terms:
y^2 + 6y = (y + 3)^2 - 9
Substituting these back into the original equation, we get:
(x + 2)^2 - 4 + (y + 3)^2 - 9 = -4
Simplifying:
(x + 2)^2 + (y + 3)^2 = 9
Now we can see that the equation is in standard form for a circle, which is:
(x - h)^2 + (y - k)^2 = r^2
Where (h, k) is the centre of the circle and r is the radius.
Comparing the two equations, we can see that the centre is (-2, -3) and the radius is 3.
Therefore, the centre of the circle is (-2, -3) and the radius is 3 units.
Learn more about radius, here:
brainly.com/question/26725967
#SPJ11
If A is symmetric matrix, then A^3 is a _______ matrix.
Answers
If A is a symmetric matrix, then A³ is also a symmetric matrix.
To prove this, we can use the definition of a symmetric matrix, which is a matrix that is equal to its transpose. In other words, if A is a symmetric matrix, then A = A^T.
Now, let's look at A³:
A³ = A * A * A
We can replace each A with A^T, since they are equal:
A³ = A^T * A^T * A^T
Now, we can use the property that the transpose of a product of matrices is equal to the product of their transposes in reverse order:
A³ = (A^T * A^T * A^T)^T
A³ = (A^T)^T * (A^T)^T * (A^T)^T
Since the transpose of a transpose is the original matrix, we can simplify:
A³ = A * A * A
Therefore, A³ is also a symmetric matrix.
More information about the symmetric matrix here:
https://brainly.com/question/16374195
#SPJ11
How much is 106 divided by 6?
A) 17 R2
B)17 R3
C)17 R4
D)17 R1
Answers
Answer:
C, 17 R4.
Step-by-step explanation:
6x17 is equal to 102, and 102+4 gets you to 106, therefor C is the correct answer.
What is the image of (10, -12) after a
dilation by a scale factor of centered at the
origin?
Answers
Answer:
-5, -3
Step-by-step explanation:
True or False: The response variable, y, and the explanatory variable, x, can be interchanged in the least squares regression line equation.
Answers
False, the response variable, y, and the explanatory variable, x, cannot be interchanged in the least squares regression line equation.
The least squares regression line equation, also known as the regression equation, is a mathematical model that represents the relationship between a response variable, denoted as y, and an explanatory variable, denoted as x. In this equation, y is the variable being predicted or estimated, while x is the variable used to explain the variation in y. The regression equation is typically written as y = mx + b, where m is the slope of the line and b is the y-intercept.
The response variable, y, represents the outcome or dependent variable in a regression analysis, while the explanatory variable, x, represents the predictor or independent variable. These variables have different roles and cannot be interchanged in the regression equation. The slope, m, represents the change in y for a one-unit change in x, and the y-intercept, b, represents the predicted value of y when x is equal to zero.
Interchanging the response variable, y, and the explanatory variable, x, in the regression equation would result in an incorrect representation of the relationship between the variables. It would imply that y is used to explain the variation in x, which is not the intended purpose of the regression model.
Therefore, it is important to correctly identify and use the appropriate response and explanatory variables in the least squares regression line equation to obtain valid and meaningful results.
To learn more about squares regression here:
brainly.com/question/28216384#
#SPJ11
Determine the discriminant for the quadratic equation -3=x2+4x+1. Based on the discriminant value, how many real number solutions does the equation have?
Discriminant = b2-4ac
0
1
2
12
Answers
Answer:
Step-by-step explanation:
3=x^2+4x+1
x^2 + 4x + 4 = 0
Discriminant = 4^2 - 4*1*4 = 0
There is one real root (multiplicity 2).
The quadratic equation is x² + 4x + 4 = 0 and the number of solution is 1
What is Quadratic Equation?A quadratic equation is a second-order polynomial equation in a single variable x , ax² + bx + c=0. with a ≠ 0. Because it is a second-order polynomial equation, the fundamental theorem of algebra guarantees that it has at least one solution. The solution may be real or complex.
The roots of the quadratic equations are
x = [ -b ± √ ( b² - 4ac ) ] / ( 2a )
where ( b² - 4ac ) is the discriminant
when ( b² - 4ac ) is positive, we get two real solutions
when discriminant is zero we get just one real solution (both answers are the same)
when discriminant is negative we get a pair of complex solutions
Given data ,
Let the quadratic equation be represented as A
Now , the value of A is
-3 = x² + 4x + 1
Adding 3 on both sides , we get
x² + 4x + 4 = 0
Now , ( b² - 4ac ) is the discriminant
So , 16 - 4 ( 4 ) = 0
0 = 0
when discriminant is zero we get just one real solution
Hence , the quadratic equation is solved
To learn more about quadratic equations click :
https://brainly.com/question/25652857
#SPJ2
A construction firm is building a skyscraper, and the height of the skyscraper in yards and feet after certain numbers of days is shown in the table below. What is the missing value in the table?
Answers
Answer:
its 918 people
Step-by-step explanation:
Answer:
its 918 people
Step-by-step explanation:
A casserole is removed from a 375oF oven and cools to 190oF after 25 minutes in a room at 68oF. How long (from the time it is a removed from the oven) will it take the casserole to cool to 105oF
Answers
Answer:
57.3 minutes
Step-by-step explanation:
We know that the temperature as a function of time of an object is described by the equation:
\(T(t) = T_a + (T_0 - Ta)*e^{-k*t}\)
Where:
k is a constant
Tₐ = room temperature = 68°F
T₀ = initial temperature of the object = 375°F
Replacing these in our equation we will get
T(t) = 68°F + (375°F - 68°F)*e^{-k*t} = 68°F + (307°F)*e^{-k*t}
And we know that after 25 minutes, at t = 25min, the temperature of the casserole is 190°F
then:
T(25min) = 190°F = 68°F + (307°F)*e^{-k*25 min}
Now we can solve this for k:
190°F = 68°F + (307°F)*e^{-k*25 min}
190°F - 68°F = (307°F)*e^{-k*25 min}
(122°F)/(307°F) = e^{-k*25 min}
Now we can apply the natural logarithm in both sides:
Ln( 122/307) = Ln(e^{-k*25 min}) = -k*25min
Ln( 122/307)/(-25 min) = k = 0.0369 min^-1
Then the temperature equation is:
T(t) = 68°F + (307°F)*e^{-0.0369 min^-1*t}
Now we want to find the value of t such that:
T(t) = 105°F = 68°F + (307°F)*e^{-0.0369 min^-1*t}
We can solve this in the same way:
105°F - 68°F = (307°F)*e^{-0.0369 min^-1*t}
37°F = (307°F)*e^{-0.0369 min^-1*t}
(37°F)/(307°F) = e^{-0.0369 min^-1*t}
Ln( 37/307) = -0.0369 min^-1*t
Ln( 37/307)/( -0.0369 min^-1 ) = 57.3 min
So after 57.3 minutes, the temperature of the casserrole will be 105°F
(Find the value of): 2m x 2-m
Answers
let a and b be orthogonally diagonalizable n × n matrices. prove or disporve (a) a b is orthogonally diagonalizable; (b) a2 is orthogonally diagonalizable.
Answers
The answer of the given question is (a) The product of two orthogonally diagonalizable matrices may not be orthogonally diagonalizable. , (b) The square of an orthogonally diagonalizable matrix is always orthogonally diagonalizable.
(a) The product of two orthogonally diagonalizable matrices may not be orthogonally diagonalizable. For example, consider the matrices:
a = [1 0; 0 -1] and b = [0 1; 1 0]
Both a and b are orthogonally diagonalizable (by themselves), since they are already diagonal matrices. However, their product ab is not diagonalizable, since
ab = [0 1; 0 -1]
which has only one distinct eigenvalue and thus cannot be diagonalized by any orthogonal matrix.
(b) The square of an orthogonally diagonalizable matrix is always orthogonally diagonalizable. To see why, let A be an n × n matrix that is orthogonally diagonalizable, so that A = QDQ^T, where Q is an orthogonal matrix and D is a diagonal matrix. Then we have
A² = (QDQ^T)(QDQ^T) = QD(Q^TQ)DQ^T = QDDQ^T
since Q is orthogonal and thus Q^TQ = I. Therefore, A² is also orthogonally diagonalizable, with the same orthogonal matrix Q and the diagonal matrix D².
To know more about Orthogonally diagonalizable visit:
https://brainly.com/question/30638339
#SPJ11
Is it true that if A and B are m×n, then both ABT and ATB are defined.
Answers
No, it is not necessarily true that both ABT and ATB are defined for matrices A and B of size m × n.
In order for the matrix product ABT to be defined, the number of columns in A (which is n) must be equal to the number of columns in BT (which is also n). This means that the number of rows in B (which is m) must be equal to the number of rows in A (which is also m). So, if A and B are both square matrices of size n × n, then ABT is defined
On the other hand, in order for the matrix product ATB to be defined, the number of columns in AT (which is m) must be equal to the number of columns in B (which is also n). This means that the number of rows in A (which is m) must be equal to the number of rows in B (which is also m). So, if A and B are both square matrices of size m × m, then ATB is defined.
However, if A and B are not square matrices, then it is possible that only one of ABT or ATB is defined, or neither of them are defined. In general, the product of two matrices is only defined if the number of columns in the first matrix is equal to the number of rows in the second matrix.
for such more question on matrices
https://brainly.com/question/14998315
#SPJ11
A small cab carries 4 people. How many small cabs will I need to transport 44 people?
Answers
Please help I’m giving out likes and etc

Answers
2 translates to 10 after being multiplied by 5
1 translated to 5 after being multiplied by 5
Hope this helped :)
If f(x) = 9x -4 and g(x) = VX-2,
what is (fºg)(6)?

Answers
Answer:
To find (fºg)(6) first find (fºg)(x)
(fºg)(x) = 9(√x - 2) - 4
(fºg)(6) = 9(√ 6 - 2) - 4
= 9√4 - 4
= 9 (2) - 4 = 18 - 4
= 14
Hope this helps
How do you find the gradient of a line between two points?; How do you find the gradient of a line segment?; What is the gradient of the line segment between (- 6 4 and (- 4 10?; What is the gradient of the line segment between the points 2 3 and (- 3 8?
Answers
The gradient of the line segment between (-6, 4) and (-4, 10) is 3, and the gradient of the line segment between (2, 3) and (-3, 8) is -1.
To find the gradient (also known as slope) of a line between two points, you can use the formula:
Gradient = (Change in y-coordinates) / (Change in x-coordinates)
To find the gradient of a line segment, you follow the same approach, calculating the change in y-coordinates and the change in x-coordinates between the two points that define the line segment.
Let's calculate the gradients for the given line segments:
1) Gradient of the line segment between (-6, 4) and (-4, 10):
Change in y-coordinates = 10 - 4 = 6
Change in x-coordinates = -4 - (-6) = 2
Gradient = (Change in y-coordinates) / (Change in x-coordinates)
= 6 / 2
= 3
Therefore, the gradient of the line segment between (-6, 4) and (-4, 10) is 3.
2) Gradient of the line segment between the points (2, 3) and (-3, 8):
Change in y-coordinates = 8 - 3 = 5
Change in x-coordinates = -3 - 2 = -5
Gradient = (Change in y-coordinates) / (Change in x-coordinates)
= 5 / -5
= -1
Therefore, the gradient of the line segment between the points (2, 3) and (-3, 8) is -1.
To know more about gradient, refer here:
https://brainly.com/question/16824780
#SPJ4
let r be a partial order on set s, and t ⊆ s. suppose that a,a′ ∈ t, where a is greatest and a′ is maximal. prove that a = a′
Answers
Let r be a partial order on set S, and let t be a subset of S. If a and a' are both elements of t, where a is the greatest element and a' is a maximal element, then it can be proven that a = a'.
To prove that a = a', we consider the definitions of greatest and maximal elements. The greatest element in a set is an element that is greater than or equal to all other elements in that set. A maximal element, on the other hand, is an element that is not smaller than any other element in the set, but there may exist other elements that are incomparable to it.
Given that a is the greatest element in t and a' is a maximal element in t, we can conclude that a' is not smaller than any other element in t. Since a is the greatest element, it is greater than or equal to all elements in t, including a'. Therefore, a is not smaller than a'.
Now, to prove that a' is not greater than a, suppose by contradiction that a' is greater than a. Since a' is not smaller than any other element in t, this would imply that a is smaller than a'. However, since a is the greatest element in t, it cannot be smaller than any other element, including a'. This contradicts our assumption that a' is greater than a.
Hence, we have shown that a is not smaller than a' and a' is not greater than a, which implies that a = a'. Therefore, if a is the greatest element and a' is a maximal element in t, then a = a'.
To learn more about contradiction click here, brainly.com/question/30373679
#SPJ11
A grocery store chain introduces a new brand of cereal in several of its stores. The function B(w)=120w150+w2 for w≥0 models the number of boxes, B, in thousands, of the cereal sold after w weeks. The graph of this function is shown below.
Select the THREE true statements regarding the graph of B(w).
A
Based on the zeros of the function, the number of boxes of cereal sold is 0 after 0 weeks.
B
Based on the zeros of the function, the number of boxes of cereal sold is 0 after 1,250 weeks.
C
Based on the end behavior of the function, the number of boxes of cereal sold will keep falling after reaching the maximum.
D
Based on the asymptote of the function, the number of boxes of cereal sold will never fall below 800 after reaching the maximum.
E
Based on the asymptote of the function, the number of boxes of cereal sold will never reach 0 after the cereal is introduced in the store.
Answers
The THREE true statements regarding the graph of B(w) are;
A) Based on the zeros of the function, the number of boxes of cereal sold is 0 after 0 weeks.
C) Based on the end behavior of the function, the number of boxes of cereal sold will keep falling after reaching the maximum.
E) Based on the asymptote of the function, the number of boxes of cereal sold will never reach 0 after the cereal is introduced in the store.
How to Interpret Quadratic Graph?
We are given the graph represented by the quadratic function;
B(w) = 120w/(150 + w²) for w ≥ 0 that models;
the number of boxes, B, in thousands, of the cereal sold after w weeks
From the graph, we can see that at the origin which is the coordinate (0, 0) that it remains so and as such the number of boxes of cereal sold is 0 after 0 weeks. Thus, option A is correct
Secondly, from the given graph, we see that the graph starts rising from zero to a maximum after which it keeps falling. Thus, we can say that option C is correct
Lastly, we see that the graph asymptote approaches 500 thousand boxes but never gets to zero and as such we can say that option E is correct.
Read more about Quadratic Graph at; https://brainly.com/question/14477557
#SPJ1

HELP!!!!!!!!!!!!!! What is the area of the triangle shown below?
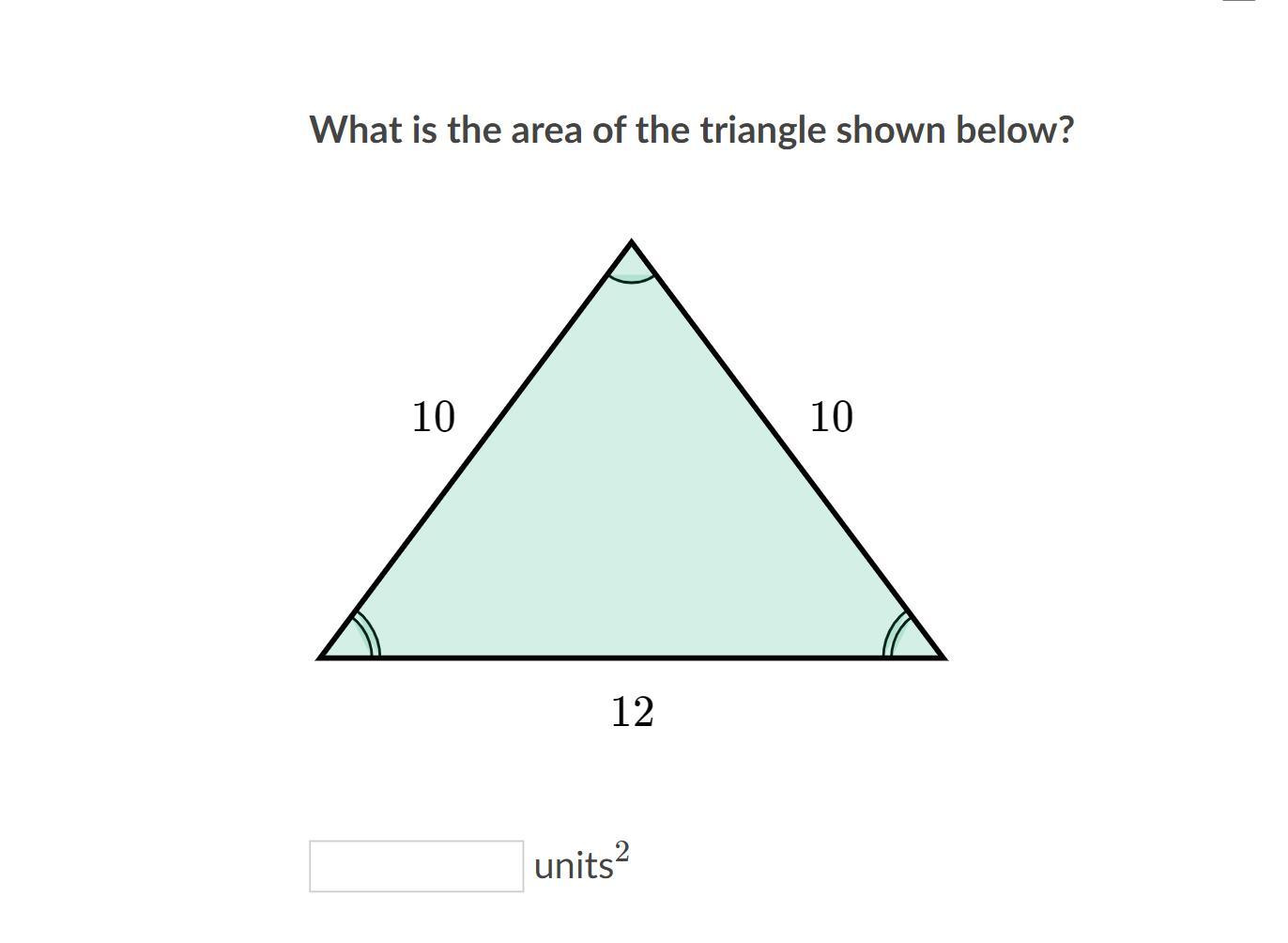
Answers
Answer:
48
Step-by-step explanation:
\(s = (10 + 10 + 12) / 2 = 16\\area = \sqrt{16(16-10)^2*(16-12)} = 48\)
PS. You can also find the area by dividing the triangle in 2 halves and then finding the height. Then the area is simply Base * Height / 2

In ΔQRS, r = 380 cm, s = 390 cm and ∠Q=48°. Find the length of q, to the nearest centimeter.
Answers
Step-by-step explanation:
Using Cosine rule, we have:
q² = r² + s² - 2(r)(s)(cosQ)
= 380² + 390² - 2(380)(390)(cos48°)
= 98169.688cm²
Hence q = 313cm. (nearest centimeter)
The required value of side q is 313 cm for the triangle ΔQRS.
What is a triangle?A triangle is a geometric figure with three edges, three angles and three vertices. It is a basic figure in geometry.
The sum of the angles of a triangle is always 180°
Given that,
In triangle QRS side r = 380 cm, side s = 390 cm and angle Q = 48°.
To find the length of the side q,
Use cosine rule,
\(cos Q = \frac{(r^2 + s^2 - q^2)}{(2\times r \times s)}\)
Substitute the values here,
\(cos 48 = \frac{(380)^2 + (390)^2- q^2}{2\times380 \times390} \\\)
\(0.67 = \frac{144400 + 152100 - q^2}{296400}\)
198,588 = 296500 - q²
q² = 97912
q = 312.90
q = 313 cm
The value of side q is 313 cm.
To know more about Triangle on:
https://brainly.com/question/2773823
#SPJ2
Question 7 of 10
What is the solution to this equation

Answers
Answer:
x = 4
Step-by-step explanation:
x + 4(x+5) = 40 (Given)
x + 4x + 20 = 40 (Distribute the 4 into the x and 5)
5x + 20 = 40 (Add like terms)
5x = 20 (Subtract 20 on both sides)
x = 4 (Divide 5 on both sides)
The United States five-dollar bill are 155.956 mm long and 66.294 wide. A stack of these bills fits inside a 156 x 66.3 x 66.3 mm box and uses up 258,473.68 cubic millimeters of volume.
Part A: How much money is in the box?
Part B: What percent of the box’s volume is taken up by the five-dollar bills?
Answers
Answer:
A) $5 × 25 = $75
B) 37.69%
Step-by-step explanation:
The dimension of five dollar bill:
Length = 155.956mm
Width = 66.294
Volume of box being occupied by 5 dollar bill = 258,473.68mm^3
Dimension of box :
156 x 66.3 x 66.3 mm
If volume of the 5—dollar bill is 258,473.68mm^3
Then, the Thickness of the five dollar stack equals :
Volume = Length × width × height
258,473.68mm^3 = 155.956mm × 66.294 × height
258,473.68 = 10338.947064 × h
h = (258473.68/10338.947064)
h = 25.000000003288 = 25
Therefore, the amount of money in the box is:
$5 × 25 = $75
Percentage of box volume taken up by $5 bill
Volume of the box:
156 x 66.3 x 66.3 mm = 685727.6399mm^3
Volume of box being occupied by 5 dollar bill = 258,473.68mm^3
(258,473.68 / 685727.6399) × 100
=37.69%