While waiting for his car to be repaired, a man rents a car for $17 per day and 33 cents per mile. His insurance
company will pay up to $200 of the rental fee. If he needs the car for four days, how many miles of driving will his
policy cover?
Answers
Answer:
$17 per day
4 days= $17 x 4= $68
$200-$68= $132
$0.33x=$132
_____. ____
$0.33. $0.33
x= 400
His policy will cover 400 miles of driving
Step-by-step explanation:
Related Questions
If the ratio of a circle's circumference to the circle's area is 2/9, then find the circles area.

Answers
The area of the circle is 81π. Option A.
What is area of a circle?The area of a given circle is the amount of space that the circle will cover when considered in a 2 dimensional plane. It can be determined by;
area of a circle = πr^2
where r is the radius.
The circumference of a circle is the curved boundary of a circle. It can be determined by;
circumference of a circle = 2πr
where r is its radius.
From the given information in the question, we have a circle's circumference to the circle's area;
circumference/ area = 2/ 9
But,
circumference/ area = 2πr/ πr^2
= 2/ r
Then;
2/ r = 2/ 9
2r = 2*9
= 19
r = 18/ 2
r = 9
Thus,
area of the circle = πr^2
= π(9)^2
= 81π
Learn more about the area of a circle at https://brainly.com/question/14068861
#SPJ1
The annual average price per square foot for office space in a city was $30.18 in 2004, and it was $66.85 in 2015.
(a) Find an exponential function of the form f(t)=y0b^t to model these data in which t=0 corresponds to 2004.
Answers
The exponential model of the given data is f(t) = 30.18 × 1.06^t.
What are the rules of exponents?Some of the rules of exponents are as follows,
The product of two exponents having the same power is equal to the power of their base multiplied.
The product of two exponents having the same base is equal to the sum of the powers of different exponents to the same base.
Given that,
The average price for office space in 2004 is $30.18.
The average price for office space in 2015 is $66.85.
Suppose the average price in 2004 is taken as y₀.
The given situation can be represented in the form of exponential function f(t) = y₀b^t as,
Take t = 0 for 2004
Then, f(0) = y₀b^0
⇒ f(0) = y₀ = $30.18.
Then, at 2015, t = 12. Substitute the respective values to get,
f(12) = 30.18 × b^12
⇒ 66.85 = 30.18 × b^12
⇒ b^12 = 66.85 / 30.18
⇒ b = 1.06
Thus in exponential form the given situation can be written as,
f(t) =30.18 × 1.06^t
Hence, the given data can be modeled in exponential function as f(t) =30.18 × 1.06^t.
To know more about exponents click on,
https://brainly.com/question/5497425
#SPJ1
Find the median of the data set.
2, 33, 23,37,45, 5,49, 27,48
A) 33
B)45
C)29.9
D)5
The answer that is in blue is mine but I’m not sure if it’s right

Answers
To find the median we have to order the numbers lowest to highest and see what’s in the middle, so;
2, 5, 23, 27, [33], 37, 45, 48, 49
solve for x . Help me solve them

Answers
\(\\(1).\\\\(1.7898)^{2x} = (1.7898)^6\\\\\implies \ln(1.7898)^{2x} = \ln(1.7898)^6\\\\\implies 2x \ln(1.7898) = 6 \ln(1.7898)\\\\\implies 2x =6\\\\\implies x = \dfrac 62 =3\\\\(3).\\\\2^{5x -6} = 4^{x+9}\\\\\implies 2^{5x -6} = (2^2)^{x+9}\\\\\implies 2^{5x-6} = 2^{2x+18}\\\\\implies \ln(2^{5x-6}) = \ln(2^{2x+18})\\\\\implies (5x -6) \ln 2 = (2x +18) \ln 2\\\\\implies 5x -6 = 2x +18\\\\\implies 5x -2x = 18 +6\\\\\implies 3x = 24\\\\\implies x = \dfrac{24}3 =8\)
through: (1, 3), perp. to y = x + 5
Answers
Answer:
y = 3x + 2
Step-by-step explanation:
Convert the equation to slope intercept form to get y = –1/3x + 2. The old slope is –1/3 and the new slope is 3. Perpendicular slopes must be opposite reciprocals of each other: m1 * m2 = –1
With the new slope, use the slope intercept form and the point to calculate the intercept: y = mx + b or 5 = 3(1) + b, so b = 2
So y = 3x + 2
g precalc Linda works 30 hours per week between two part-time jobs: When she works as a waitress she receives $11.75 per hour and when she works as a math tutor she received $ 17.5 0 per hour. Since she has only 30 hours each week that she can work, the more hours she spends at one job, the fewer number of hours she can work at the second job. If Linda worked a total of 30 hours last week and she worked 9 of these hours as a waitress, how much money did she make last week working at both jobs
Answers
Answer:
She made $105.75 working as a waitress
She made $367.50 working as a maths tutor
Step-by-step explanation:
Linda worked a total of 30 hours last week and she worked 9 of these hours as a waitress.
Hence, the number of hours worked as a maths tutor =
30 - 9
= 21 hours
When she works as a waitress she receives $11.75 per hour
Hence, $11.75 × 9 hours
= $105.75
Hence, she made $105.75 working as a waitress
When she works as a math tutor she received $ 17.50 per hour.
$17.50 × 21 hours
$367.50
Hence, she made $367.50 working as a waitress
Suppose you have a group of 20 people, 7
are women and the remaining people are
men. What is the probability you select 4
women from the group?
Answers
The probability of select 4 women from the group is, P = 35.
What is probability?
The area of mathematics known as probability deals with numerical descriptions of how likely it is for an event to happen or for a proposition to be true. A number between 0 and 1 is the probability of an event, where, roughly speaking, 0 denotes the event's impossibility and 1 denotes its certainty.
Given: You have a group of 20 people, 7 are women and the remaining people are men.
7 are women then 13 are men.
No. of ways in which 4 women can be chosen from 7 women are 7C4.
So, the probability of select 4 women from the group is,
\(P = {7_C_4} \\P = \frac{7!}{4!*(7-4)!} \\P=\frac{7!}{4!*3!} \\P = 35\)
Hence, the probability of select 4 women from the group is, P = 35.
To know more about probability, click on the link
https://brainly.com/question/24756209
#SPJ1
Answer the following question, and show your work. *
2
4
3
6
6
3
8
9
7
9
8
???
Answers
Answer:
6
(If you like this answer i would appreciate if u give brainliest but otherwise, i hope this helped ^^)
Step-by-step explanation:
To find the missing number in the given sequence, let's analyze the pattern:
2, 4, 3, 6, 6, 3, 8, 9, 7, 9, 8, ???
Looking at the sequence, we can identify a few patterns:
The sequence alternates between increasing and decreasing numbers.
The first two numbers, 2 and 4, are increasing.
The next two numbers, 4 and 3, are decreasing.
The following two numbers, 3 and 6, are increasing.
The subsequent two numbers, 6 and 3, are decreasing.
The next two numbers, 3 and 8, are increasing.
The subsequent two numbers, 8 and 9, are increasing.
Based on these observations, it appears that the sequence is following a pattern where it alternates between increasing and decreasing numbers, but the specific values being added or subtracted are not consistent.
Now let's determine the missing number:
From the pattern, the next two numbers should be decreasing. Following the pattern of alternating between increasing and decreasing numbers, the missing number after the last given number (8) should be less than 9.
Let's assume the missing number is x:
8 - x
Since the previous decreasing sequence was 6 - 3, we can assume that x is 1 less than the previous number (3):
8 - (3 - 1) = 8 - 2 = 6
Therefore, the missing number in the sequence is 6.
The complete sequence is:
2, 4, 3, 6, 6, 3, 8, 9, 7, 9, 8, 6
Una sala de cine de New York vende las entradas para niños a 3 dólares y las de los adultos a 5 dólares. Si para ver una película pueden ingresar tanto niños como adultos y en un día
ingresan 345 espectadores, recaudando por concepto de venta de boletas 1365 dólares. Se
puede afirmar que el número de niños y adultos que ingresaron fue:
Answers
A la sala de cine ingresaron 180 niños y 165 adultos.
¿Cuántos niños y adultos ingresaron a una sala de cine?
De acuerdo con el enunciado, la sala de cine tiene capacidad para 345 espectadores y cobra 3 dólares por cada niño y 5 dólares por cada adulto. Asimismo, esta sala tiene un recaudo diario de 1365 dólares. La situación puede ser sintetizada en la siguiente ecuación algebraica:
3 · x + 5 · (345 - x) = 1365
Donde x es el número de niños que asistieron a la sala de cine.
Ahora despejamos la variable correspondiente mediante propiedades algebraicas:
3 · x + 1725 - 5 · x = 1365
1725 - 2 · x = 1365
2 · x = 1725 - 1365
2 · x = 360
x = 180
Ahora, el número de adultos es:
y = 345 - 180
y = 165
Para aprender más sobre ecuaciones algebraicas: https://brainly.com/question/20307002
#SPJ1
find the non permissible replacement for (x ^ 2 + 1)/(2x + 10)
Answers
Reason:
We cannot divide by zero. This means the denominator cannot equal zero. If it was zero, then,
2x+10 = 0
2x = -10
x = -10/2
x = -5
Follow that chain in reverse to see that x = -5 causes the denominator 2x+10 to be zero. This is why we kick -5 out of the domain. Any other x value is valid.
I invested $750 and earned 16% yearly interest
Write the equation
Complete the table
Answers
The equation to calculate the yearly interest earned on your investment of $750 at a 16% interest rate is: Interest = $750 * 0.16.
To write the equation for calculating the yearly interest earned on an investment, we can use the formula:
Interest = Principal * Rate
Where:
- Principal is the initial investment amount.
- Rate is the interest rate expressed as a decimal.
In this case, you invested $750, and the annual interest rate is 16%. To use the decimal form of the interest rate, we divide it by 100:
Rate = 16% = 16/100 = 0.16
Substituting the values into the equation:
Interest = $750 * 0.16
To calculate the interest, we multiply the principal by the interest rate:
Interest = $750 * 0.16 = $120
Therefore, the equation to calculate the yearly interest earned on your investment of $750 at a 16% interest rate is:
Interest = $750 * 0.16
Now, let's complete a table to show the growth of your investment over multiple years. We'll assume the interest is compounded annually.
Year | Initial Investment | Interest Earned | Total Value
---------------------------------------------------------
1 $750 $120 $870
2 $870 $139.20 $1009.20
3 $1009.20 $161.47 $1170.67
4 $1170.67 $187.31 $1357.98
5 $1357.98 $217.28 $1575.26
In each year, we calculate the interest earned by multiplying the initial investment by the interest rate (16% or 0.16). The total value is obtained by adding the initial investment and the interest earned. This process is repeated for each subsequent year.
The table shows the growth of your investment over five years, demonstrating how the interest compounds and increases the total value each year.
more such question on interest visit
https://brainly.com/question/25720319
#SPJ8
(-6+1 1/2+5)^2...I'm getting 1 but when I put it in the calculator I get .25...What am I do wrong?
Answers
Answer:
Step-by-step explanation:
your doing the calculation wrong
solve the following equation by completing the square. x^2-8x-2=0
Answers
\(x^2 -8x-2=0\\\\x^2 -8x=2\\\\x^2 -8x+16=18\\\\(x-4)^2 =18\\\\x-4=\pm \sqrt{18}\\\\\boxed{x=4 \pm \sqrt{18}}\)
19.14 = v + 1.5
v = ?
Answers
Answer:
V= 17.64
Step-by-step explanation:
The sum of three numbers is 18. The sum of twice the first number, 5 times the second number, and 6 times the third number is 79. The difference between 8 times the first number and the second number is 43. Find the three numbers.
Answers
Answer:
The three numbers are 5,6&7


Help me please it’s due today please help me please help me please help me please help me please help me?
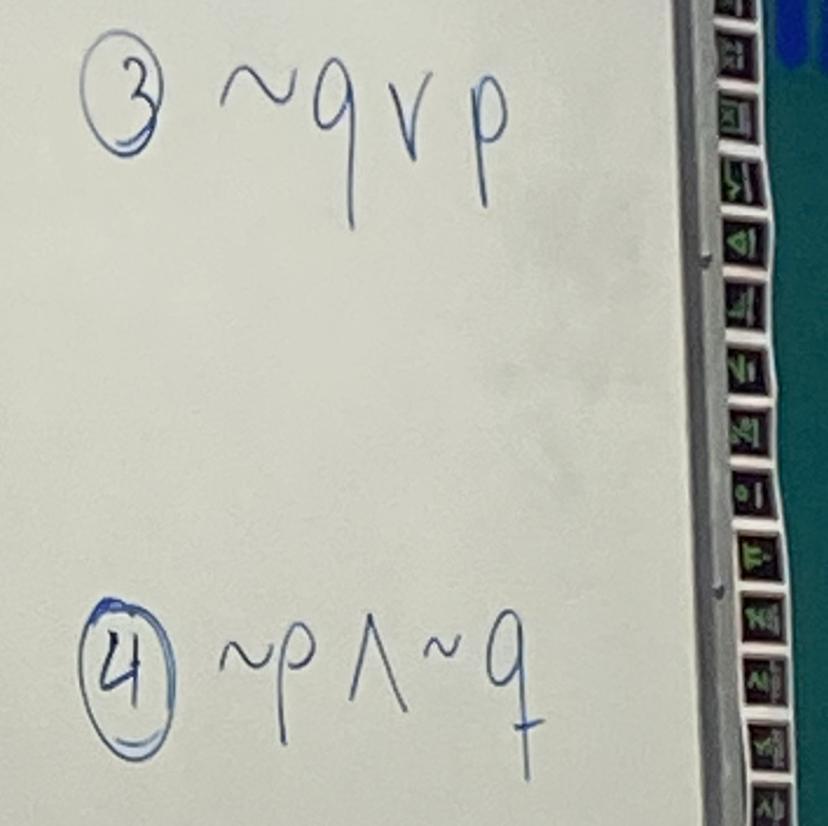
Answers
The results of the logical expressions are
¬ q v p: false if q is true and p is false¬ p ∧ ¬ q: true if q is false and p is falseWhat are logical expressions?Logical expressions are expressions that have a result of true or false.
These results are generally classified as boolean values
How to solve the logical expressions?We start by solving the first expression
Logic expression (3)
¬ q v p
The above expression uses the or operator
The rule of the or operator is that:
It evaluates to true, if at least one of the terms is trueOtherwise, it is falseThis means that the expression ¬ q v p evaluates to false if q is true and p is false; otherwise, it evaluates to true
Logic expression (4)
¬ p ∧ ¬ q
The above expression uses the and operator
The rule of the and operator is that:
It evaluates to true, if both terms are trueOtherwise, it is falseThis means that the expression ¬ p ∧ ¬ q evaluates to true if q is false and p is false; otherwise, it evaluates to false
Read more about logical expressions at
https://brainly.com/question/15078651
#SPJ1
Answer:The results of the logical expressions are¬ q v p: false if q is true and p is false¬ p ∧ ¬ q: true if q is false and p is falseWhat are logical expressions?Logical expressions are expressions that have a result of true or false.These results are generally classified as boolean valuesHow to solve the logical expressions?We start by solving the first expressionLogic expression (3)¬ q v pThe above expression uses the or operatorThe rule of the or operator is that:It evaluates to true, if at least one of the terms is trueOtherwise, it is falseThis means that the expression ¬ q v p evaluates to false if q is true and p is false; otherwise, it evaluates to trueLogic expression (4)¬ p ∧ ¬ qThe above expression uses the and operatorThe rule of the and operator is that:It evaluates to true, if both terms are trueOtherwise, it is falseThis means that the expression ¬ p ∧ ¬ q evaluates to true if q is false and p is false; otherwise, it evaluates to false
Step-by-step explanation:
Let ABCD be a trapezoid with bases AB and CD. Let P be a point on side CD, and let X, Y be the feet of the altitudes from P to AD, BC respectively. Prove that if AD = 5, BC = 7, AB = 6, CD = 12, and CP/PD = 1, then PX = 12*sqrt(6)/5 and PY = 12*sqrt(6)/7.
Answers
The statement is proved: PX = 12√6/5 and PY = 12√6/7.
To prove that PX = 12√6/5 and PY = 12√6/7, we will use the properties of similar triangles and the Pythagorean theorem.
First, let's denote the intersection point of the diagonals as O.
We know that triangle ABP is similar to triangle CDP, as they share the same angles due to being vertical angles.
Therefore, we can write the following proportion:
AB/CD = BP/PD
Substituting the given values, we have:
6/12 = BP/PD
Simplifying, we find:
BP = PD/2
Since CP/PD = 1, we can conclude that CP = PD.
Now, let's consider triangle ABP and triangle CBO.
These triangles are similar because they share the same angles (due to being vertical angles) and have proportional sides.
We can write the following proportion:
AB/BC = BP/CO
Substituting the given values, we have:
6/7 = BP/CO
Rearranging the equation, we find:
CO = (7/6)BP
Now, let's focus on triangle ODP.
Using the Pythagorean theorem, we can write the following equation:
\(OD^2 = OP^2 + PD^2\)
Since we want to find PX and PY, which are the altitudes from P to AD and BC respectively, we need to express OP in terms of PX and PD, and OD in terms of PY and PD.
Looking at triangle ODP, we can see that OP = PX + OX and OD = PY + OY.
Substituting these expressions into the Pythagorean theorem equation, we have:
\((PX + OX)^2 = OP^2 = (PY + OY)^2 + PD^2\)
Expanding and simplifying the equation, we get:
\(PX^2 + 2PXOX + OX^2 = PY^2 + 2PYOY + OY^2 + PD^2\)
Since OX = OY = 0 (the altitudes are perpendicular to the bases), the equation simplifies to:
\(PX^2 = PY^2 + PD^2\)
Now, let's substitute the given values into this equation:
\((PX)^2 = (12\sqrt{6/7} )^2 + (PD)^2\)
Simplifying further, we get:
\((PX)^2 = 72/7 + (PD)^2\)
We know that PD = CP = CD - CP = 12 - PD, so we substitute this expression into the equation:
\((PX)^2 = 72/7 + (12 - PD)^2\)
Now, we can solve for \((PX)^2:\)
\((PX)^2 = 72/7 + 144 - 24PD + (PD)^2\)
Simplifying, we find:
\((PX)^2 = 216/7 - 24PD + (PD)^2\)
Since CP/PD = 1, we can write PD = 12 - PD, which gives us PD = 6.
Substituting this value into the equation, we have:
\((PX)^2 = 216/7 - 24(6) + (6)^2\)
Simplifying further, we get:
\((PX)^2 = 72/7\)
Taking the square root of both sides, we find:
PX = √(72/7) = 12√6/5
Similarly, we can prove that PY = 12√6/7.
For similar question on triangles.
https://brainly.com/question/17264112
#SPJ11

8 x 5/6 please answer this question i really need help with it.
Answers
Answer:
20/3
Step-by-step explanation:
Start with multiplying the numerator by 5, keep the 6 then simply,
A box has a width of 10 cm and a length of 17 cm. The volume of the box is decreasing at a rate of 527 cubic cm per minute, with the width and length being held constant. What is the rate of change, in cm per minute, of the height when the height is 6 cm?
Round your answer to the nearest hundredth. (Do not include any units in your answer.)
Answers
Therefore, the rate of change, in cm per minute, of the height when the height is 6 cm is approximately -6 cm/min.
Given,The width of the box = 10 cm Length of the box = 17 cmThe volume of the box = 527 cubic cm/minWe need to find the rate of change, in cm per minute, of the height when the height is 6 cm.We know that the volume of the box is given as:V = l × w × h where, l, w and h are length, width, and height of the box respectively.It is given that the width and length are being held constant.
Therefore, we can write the volume of the box as
:V = constant × h Differentiating both sides with respect to time t, we get:dV/dt = constant × dh/dtNow, it is given that the volume of the box is decreasing at a rate of 527 cubic cm per minute.
Therefore, dV/dt = -527.Substituting the given values in the above equation, we get:
527 = constant × dh/dt
We need to find dh/dt when h = 6 cm.To find constant, we can use the given values of length, width and height.Substituting these values in the formula for the volume of the box, we get:
V = l × w × hV = 17 × 10 × hV = 170h
We know that the volume of the box is given as:V = constant × hSubstituting the value of V and h, we get:
527 = constant × 6 cm
constant = 87.83 cm/minSubstituting the values of constant and h in the equation, we get
-527 = 87.83 × dh/dtdh/dt = -6.0029 ≈ -6 cm/min
For such more question on Length
https://brainly.com/question/28108430
#SPJ8
The height of a right triangular prism is 1 5/6 inches each side of the triangular base measures 10 inches and the height of the bases eight2 over 3 inches the triangular prism is place to top of cube whose side measures 10 inches so that one of the triangular prisms bases lies completely on one side of the cube what is the surface area of the solid formed
Answers
The surface area of the solid formed is approximately, 598.3 in².
What is the Surface Area of a Right Triangular Prism?Surface area of the solid is the area covered by the solid all round.
The given parameters are:
Height of the prism (L) = 1 5/6 = 1.83 in.Side of base (s1) = 10 in.Side of base (s2) = 10 in.Side of base (s3) = 8 2/3 = 8.67 in.base (b) = 10Height (h) = 8.67 in.a = 10 in.Surface area of the solid formed = 5(10×10) + (0.5×10×8.67) + 3(10×1.83) = 598.3 in²
Learn more about surface area of right triangular prism on:
https://brainly.com/question/27232541
#SPJ1
54 is what percent of 24? Enter your answer in the box.
Answers
Answer:
225%
2*24=48, with 6 leftover. 6 is 25% of 24, so 200% (From when we multiplied 24 by 2) plus 25% (from the remainder) = 225%
How many terms of the sequence -9, -6, -3, ... must be
taken so that the sum is 66?
Answers
Answer:
11th term
Step-by-step explanation:

One rectangle is "framed" within another. Find the area of the shaded region if the "frame" is 3 units wide.

Answers
The area of the shaded region, with a frame of 3 units wide, is 264 square units. The inner rectangle is 6x4 units, and the outer rectangle is 18x16 units.
To solve the given problem, we have to find the area of the shaded region if the frame is 3 units wide. If the frame is 3 units wide, then the dimensions of the inner rectangle (the shaded region) will be (12 - 6) × (10 - 6) which simplifies to 6 × 4.
Therefore, we can say that the inner rectangle has a length of 6 units and a width of 4 units.The dimensions of the outer rectangle are (12 + 3 + 3) × (10 + 3 + 3) which simplifies to 18 × 16. Therefore, we can say that the outer rectangle has a length of 18 units and a width of 16 units.
The area of the shaded region can be obtained by subtracting the area of the inner rectangle from the area of the outer rectangle. Therefore, the Area of the outer rectangle = length × width= 18 × 16 = 288 square units
Area of the inner rectangle = length × width= 6 × 4 = 24 square units
Area of the shaded region = Area of the outer rectangle - Area of the inner rectangle = 288 - 24= 264 square units
Therefore, the area of the shaded region is 264 square units.
For more questions on the area of the shaded region
https://brainly.com/question/23973962
#SPJ8
Find the product. 7. $458.29 × 6.3% 8. $280.12 × 7.75%
Answers
Answer:
7. 28.8722
8. 21.7093
Step-by-step explanation:
458.29 x .063=28.8722
21.7093 x .0775= 21.7093
I need to know the percentage of drivers who are at least 45. Using the table in the picture.

Answers
The percentage of drivers who are at least 45 is 62%
How to determine the percentage of drivers who are at least 45.From the question, we have the following parameters that can be used in our computation:
The table of values
From the table, we have
Age 45 = 62 percentile
When represented properly
So, we have
Age 45 = 62%
This means that the percentage of drivers who are at least 45 is 62%
Read more abot percentage at
https://brainly.com/question/24877689
#SPJ1
Solve:
y = x- 4
y = 6x - 10
Answers
Answer:1.2
Step-by-step explanation:
then,
x-4=6x-10
-5x=-6
x=1.2
Math 1-2 High School please help due in two minutes

Answers
The sum of the interior angle of a rhombus is 360° and each angle is 90°
Can I please get some help I’ve been stuck on this question for a while!

Answers
Using the radius of the Ferris wheel and the angle between the two positions, the time spent on the ride when they're 28 meters above the ground is 12 minutes
How many minutes of the ride are spent higher than 28 meters above the ground?The radius of the Ferris wheel is 30 / 2 = 15 meters.
The highest point on the Ferris wheel is 15 + 4 = 19 meters above the ground.
The time spent higher than 28 meters is the time spent between the 12 o'clock and 8 o'clock positions.
The angle between these two positions is 180 degrees.
The time spent at each position is 10 minutes / 360 degrees * 180 degrees = 6 minutes.
Therefore, the total time spent higher than 28 meters is 6 minutes * 2 = 12 minutes.
Learn more on a Ferris wheel here;
https://brainly.com/question/30524034
#SPJ1
Two cars are traveling towards a hotel on the same road. From the edge of the hotel, 600 feet high, Spiderman sits on the rooftop thinking about the depression angle needed to reach each car. If the depression angle to the nearest car is 52 degrees, and the depression angle to the farther car is 46 degrees, how far apart must the two cars be from each other?
Make a sketch, solve the problem, and round your answer to the nearest hundredth of a foot.
Answers
The two cars must be approximately 177.34 feet apart from each other for Spiderman to have different depression angles to each car.
To find the distance between the two cars, we can use trigonometry and the concept of similar triangles. Let's denote the distance between Spiderman and the nearest car as d1 and the distance between Spiderman and the farther car as d2.
In a right triangle formed by Spiderman, the height of the hotel, and the line of sight to the nearest car, the tangent of the depression angle (52 degrees) can be used:
tan(52) = 600 / d1
Rearranging the equation to solve for d1:
d1 = 600 / tan(52)
Similarly, in the right triangle formed by Spiderman, the height of the hotel, and the line of sight to the farther car, the tangent of the depression angle (46 degrees) can be used:
tan(46) = 600 / d2
Rearranging the equation to solve for d2:
d2 = 600 / tan(46)
Using a calculator, we can compute:
d1 ≈ 504.61 feet
d2 ≈ 681.95 feet
The distance between the two cars is the difference between d2 and d1:
Distance = d2 - d1
Plugging in the values, we have:
Distance ≈ 681.95 - 504.61
Distance ≈ 177.34 feet
For more such question on angles. visit :
https://brainly.com/question/25770607
#SPJ8
Given sinz = -4/5 for pi < z < (3pi)/2, find the value of cosz.

Answers
The angle z is in the third quadrant, the value of cosz is negative. Hence, cosz = -3/5.So, the value of cosz is -3/5.
Given sinz = -4/5 for pi < z < (3pi)/2, we need to find the value of cosz. We can use the trigonometric identity of Pythagorean theorem to find the value of cosz.
According to Pythagorean theorem, sin2θ + cos2θ = 1, where θ is the angle in the right-angled triangle and sin, cos are the trigonometric ratios.
The negative sign for the given sinz indicates that the angle z is in the third quadrant. So, we can take the help of the unit circle to find the value of cosz as shown below:
Here, we have used the Pythagorean identity of sin2z + cos2z = 1 on the unit circle to find the value of cosz. Since the value of sinz is already given, we can find the value of sin2z as: sin2z = sinz x sinz = (-4/5) x (-4/5) = 16/25
Then, we can substitute the value of sin2z in the Pythagorean identity as: cos2z = 1 - sin2z = 1 - (16/25) = 9/25We need to find the value of cosz.
So, we can take the square root of cos2z as: cosz = ±(√(9/25)) = ±(3/5)The sign of cosz can be determined by considering the quadrant of the angle z.
Since the angle z is in the third quadrant, the value of cosz is negative. Hence, cosz = -3/5.So, the value of cosz is -3/5.
For more questions on angle.
https://brainly.com/question/31615777
#SPJ8