Which theorem or postulate proves that △ABC and △DEF are similar?
The two triangles are similar by which postulate or theorem?
SAS Similarity Theorem
SSS Similarity Theorem
AA Similarity Postulate

Answers
Answer:
AA Similarty
Step-by-step explanation: We are given that two angles are congruent so we use AA SImilarity. Stating that if two angles are congruent, then the figures are similar.
The postulate that can be used to prove that triangles ABC and DEF are similar triangles is: C. AA Similarity Postulate.
What is the AA Similarity Postulate?The AA similarity postulate states that when two triangles have two pairs of corresponding angles that are congruent to each other, the two triangles are regarded as similar triangles.
Thus, triangles ABC and DEF have:
two pairs of congruent angles - ∠B ≅ ∠E and ∠C ≅ ∠F.
Therefore, the postulate that can be used to prove that triangles ABC and DEF are similar triangles is: C. AA Similarity Postulate.
Learn more about the AA Similarity Postulate on:
https://brainly.com/question/2166570
Related Questions
49 47 43 50 45 49 49 49 43 50 43 47 47 46 45 49 50 49 43 50 46 46 50 48 47 49 47 46 43 48 50 47 46 Calculate the standard deviation with your calculator. (Round to the nearest tenth)
Answers
Answer:
qw
Step-by-step explanation:
w
Answer:50
Step-by-step explanation:
What is 3/11 simplified
Answers
Please help
h(x)
=
3x2 – 2x + 13
h(3) = [?]
Be sure to simplify your answer.
![Please helph(x)=3x2 2x + 13h(3) = [?]Be sure to simplify your answer.](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/vELVCSKqKBM4oqKdlj7yD1Yd3Eb8iety.png)
Answers
Answer:
34
Step-by-step explanation:
h(x)=3x² – 2x + 13
By replacing x with 3, we get
h(3)=3×3² – 2×3 + 13
=3×9-6+13
=27+7
=34
In the triangle below, angle B measures 60° and BC is 18. What is the length of AC?
Right triangle A B C is shown. Side B C is the hypotenuse.
9 StartRoot 3 EndRoot
StartFraction 9 Over StartRoot 3 EndRoot EndFraction
9
StartFraction StartRoot 3 EndRoot Over 9 EndFraction
Answers
Answer:
The Answer is D StartFraction StartRoot 3 EndRoot Over 9 EndFraction
Step-by-step explanation:
Answer:
the answer is D
Step-by-step explanation:
Trust me edge 2022
derive the transfer function for the integrator of (figure 1). express your answer in terms of frequency f and imaginary unit j . express the coefficients using three significant figures. a(f)
Answers
The transfer function for the given integrator circuit in terms of frequency,f and imaginary unit,j is expressed as \(T(f)=-j0.00628f\)
The figure of the integrator is shown at bottom of the answer.
The transfer function of an integrator can be expressed in form of impedances of the circuit elements connected to the op-amp.
Assume the impedance at the input side be \(Z_1\) and impedance of the feedback be \(Z_2\)
We can observe that at input, in consists of capacitor with capacitance,C \(= 0.1\mu F=10^{-7}F\)
and at the feedback loop, the circuit element is a resistor with resistance,R \(= 10k\Omega = 10^4 \Omega\)
Now,
the transfer function for an integrator can be written as ,
\(T(f) = -\frac{Z_2}{Z_1}\)
We know that,
impedance of capacitor is \(Z_1=\frac{1}{j\omega C}=\frac{1}{j2\pi f C}\)
impedance of resistor is \(Z_2=R\)
Now,
\(T(f)=-\frac{R}{\frac{1}{j2\pi fC}}\\\\T(f)=-R*j2\pi f C\\\\T(f)=-j10^4*2\pi f 10^{-7}\\\\T(f)=-j0.00628f\)
Hence, the transfer function is \(T(f)=-j0.00628f\)
To learn more about integrator refer here
https://brainly.com/question/28852807
#SPJ4

which angles are equivalent to 65 degreese

Answers
Step-by-step explanation:
angles are equivalent to 65 degrees :
<2, <4 & < 8
what is the area of the figure

Answers
Answer:
Explanation:
So you want to start by finding the area of the big square.
We know the width of the big square is 60cm. The length of the big square is
19
+
24
+
13
=
56
Big square
A
r
e
a
=
L
⋅
W
=
56
⋅
60
=
3360
Now let’s find the little square inside the bigger square. We see from the picture that the width is 34 and the length is 24cm. Using the same formula, we can find the area of the little square.
Little square
A
r
e
a
=
L
⋅
W
=
24
⋅
34
=
816
The area is enclosed in the area of the big square minus the area of the little square.
3360
−
816
=
2544
So the area enclosed is
2544
c
m
2
Step-by-step explanation:
Based on the figure below, what is the value of x?
(5x + 15)
01
09
0 11
15
20°
Answers
Answer:
undefined
Step-by-step explanation:
because
the figure does not appear
HELP ASAP what's the reason for statement 3, WILL GIVE BRAINLIEST

Answers
Answer:
From prove
Step-by-step explanation:
from prove
Explanation
Two angles are called complementary when their measures add to 90 degrees
Which transformation results in the function?

Answers
The transformations of f(x) are (a) a horizontal shrink by a factor of 1/4,
How to describe the transformation from the parent function?From the question, we have the following functions that can be used in our computation:
f(x) = x²
g(x) = (4x)²
Mathematically, these equations can be represented as
g(x) = f(4x)
The above equations implies that, we have the transformation to be:
The 4x implies that the function f(x) is horizontally shrunk by a factor of 1/4
Hence, the transformed function is (a)
Read more about transformation at
brainly.com/question/27224272
#SPJ1
you want to reach $3,000 in savings over four years your account will earn 10% interest per year how much must you save each month
Answers
You would need to save approximately $56.62 each month to achieve your savings goal of $3,000.00 over four years.
To calculate the monthly savings required to reach a savings goal of $3,000.00 over four years with a 10% annual interest rate, we can use the PMT (Payment) function.
The PMT function helps us determine the fixed payment amount needed to achieve a specific future value within a given time frame.
Let's break down the given information:
Present Value (PV): $0.00 (initial account balance)
Future Value (FV): $3,000.00 (savings goal)
Interest Rate (rate): 10% per year (annual interest rate)
Number of Periods (nper): 4 years (48 months)
Using the PMT function, we need to plug in the values and solve for the monthly payment (savings amount).
The formula for the PMT function is:
PMT(rate, nper, pv, [fv], [type])
Where:
rate = Interest rate per period
nper = Total number of periods
pv = Present value (initial account balance)
fv = Future value (savings goal)
type = (Optional) Indicates whether the payment is made at the beginning (1) or end (0) of the period.
We'll assume 0 for monthly savings.
Let's calculate the monthly savings using the PMT function:
PMT(10%/12, 4*12, 0, -3000, 0)
Here, we divide the annual interest rate by 12 to get the monthly interest rate (10%/12), multiply the number of years by 12 to get the total number of months (4*12), set the initial account balance (pv) as $0, set the future value (fv) as -$3,000 (negative because it's an outgoing payment), and assume the savings are made at the end of each month (type = 0).
Using a financial calculator or spreadsheet software, the monthly savings required to reach the goal of $3,000.00 over four years with a 10% annual interest rate is approximately $56.62.
Therefore, you would need to save approximately $56.62 each month to achieve your savings goal of $3,000.00 over four year.
For similar question on annual interest rate.
https://brainly.com/question/29059795
#SPJ11
Question : you want to reach $3,000.00 in savings over four years. Your account will earn 10% interest per yea Initially your account has a zero balance. How much must you save each month to achieve this goal? Use the PMT() function. Look it up in the e-book if you do not know how to use it. TIP: This is monthly so do not forget to adjust the interest rate and number of payment.
bought g gallons of gasoline for $4.55 per gallon and c cans of oil for $5.15 per can.
Answers
Joe bought 9.6 gallons of gasoline and 8 cans of oil, all in all he spent $91.12.
what is equation?An equation is a mathematical statement that is made up of two expressions connected by an equal sign.
Given:
Joe bought g gallons of gasoline for 4.55,
can be represented as 4.95g.
He bought c cans of oil for 5.45,
can be represented as 5.15c.
Add them together to find the total cost, and it will look like this: y(cost) = 4.95g + 5.45c.
b. g = 9.6 gallons
c = 8 cans of oil
the equation can be written as
y(cost) = 4.95(9.6) + 5.45(8)
y = 47.52 + 43.6
y = 91.12
Hence, if Joe bought 9.6 gallons of gasoline and 8 cans of oil, all in all he spent $91.12.
Learn more about equation here:
https://brainly.com/question/10413253
#SPJ2
The question attached here is incomplete
The complete question is:
Joe bought g gallons of gasoline for $ 4.95 per gallon and c cans of oil for $ 5.45 per can.
a. What expression can be used to determine the total amount Joe spent on gasoline and oil?
b. If he bought 9.6 gallons of gasoline and 8 cans of oil, how much did he spend in all?
Gwen, Tristan and Keith like to work out at the gym . They each have an app on their phone that estimates the calories they burn . By the time Tristan and Keith started exercising, Gwen had already burned 100 calories. Gwen burns 10 calories every minute, Tristan burns 125 every 10 minutes, and Keith burns 300 calories every 30 minutes. Let x represent the number of minutes since Tristan and Keith started exercising and y represent the number of app-estimated calories burned
Answers
Based on the above scenario, an equation that shows how much Gwen paid. The equation for Gwen is y = 100 + 10x
The equation for Tristan is y = 12.5xThe equation for Keith is y = 10x.What is the equation about?Since Gwen burns about 10 cal/min. THen she had used up 100 calories if Tristan and Keith began ar (Y g=100 if x=0)
Then Y(g)= 10x + 100
Since Tristan is known to burns 125 cal in 10 minutes always, then one can write her own as 12.5 cal every minute.
Therefore Y (t) = 12.5x
Since Keith burns 300 calories in 30 min always, or 10 calories in every minute.
Then Y (k) = 10x
The general function of y:
y=10x +100 + 12.5x + 10x
y = 32.5x + 100
Therefore, Based on the above scenario, an equation that shows how much Gwen paid. The equation for Gwen is y = 100 + 10x
The equation for Tristan is y = 12.5xThe equation for Keith is y = 10x.Learn more about calories from
https://brainly.com/question/6535979
#SPJ1
Kate recorded the number of minutes she read each day for the last two weeks in the table. Week 1 Week 2 Sunday 85 55 Monday 35 50 Tuesday 50 45 Wednesday 60 45 Thursday 30 40 Friday 35 30 Saturday 50 50 How can Kate figure out which week had the larger range in minutes read?
Answers
Answer:
By arranging the data set.
Week one has the highest range of 55 minutes
Step-by-step explanation:
Range = highest data minus lowest data.
So lers arrange our data and determine the range of each week
Week 1
Sunday 85, monday 35, Tuesday 50, Wednesday 60, Thursday 30, Friday 35, Saturday 50
Acsending order
=30, 35, 35,50,50 ,60,85
Range = 85-30 = 55
Week 2
Sunday 55 ,Monday 50, Tuesday 45 Wednesday 45 ,Thursday 40 ,Friday 30 ,Saturday 50
Acsending order
= 30,40,45,45,50,50,55,
Range=55-30 = 25
Week one has the highest range of 55 minutes
Answer:
A) 1. Order the minutes for each week.
2. Find the range for each week.
3. Compare the ranges.
Week 1 had the larger range in minutes.
Step-by-step explanation:
edg2020

Please Please Please help (6+6)/4
Answers
Answer:3
Step-by-step explanation:
Answer:
4
Step-by-step explanation:
cos a(2sec a+tan a)(sec a-2tan a)=2cos a-3tan a
Answers
The trigonometric identity cos a(2sec a + tan a)(sec a - 2tan a) = 2cos a - 3tan a
What are trigonometric identities?Trigonometric identities are equations that contain trigonometric ratios.
Given the trigonometric identity cos a(2sec a + tan a)(sec a - 2tan a) = 2cos a - 3tan a, we need to show that Left hand side (L.H.S) equals Right hand side (R.H.S). We proceed as follows
L.H.S = cos a(2sec a + tan a)(sec a - 2tan a)
Expanding the brackets, we have that
cos a(2sec a + tan a)(sec a - 2tan a) = cos a(2sec² a - 4tan asec a + tan a sec a - 2tan² a)
= cos a(2sec² a - 3tan a sec a - 2tan² a)
Now using the trigonometric identity 1 + tan² a = sec² a, we have that
cos a(2sec² a - 3tan a sec a - 2tan² a) = cos a(2(1 + tan² a) - 3tan a sec a - 2tan² a)
= cos a(2 + 2tan² a - 3tan a sec a - 2tan² a)
Collecting like terms in the equation, we have that
= cos a(2 + 2tan² a - 2tan² a - 3tan a sec a)
= cos a(2 + 0 - 3tan a sec a)
= cos a(2 - 3tan a sec a)
Expanding the bracket, we have that
= 2cos a - cos a × 3tan a sec a
= 2cos a - cos a × 3tan a/cos a (since sec a = 1/cos a)
= 2cos a - 1 × 3tan a
= 2cos a - 3tan a
= R.H.S
So, since L.H.S = R.H.S,
cos a(2sec a + tan a)(sec a - 2tan a) = 2cos a - 3tan a
Learn more about trigonometric identities here:
https://brainly.com/question/29722989
#SPJ1
Sugar canes have lengths X that are normally distributed with mean 365.45 cm and standard deviation 4.9 cm what is the probability of the length of a randomly selected Cane being between 360 and 370 cm
Answers
Answer:
The probability of the length of a randomly selected Cane being between 360 and 370 cm P(360 ≤X≤370) = 0.6851
Step-by-step explanation:
step(i):-
Let 'X' be the random Normal variable
mean of the Population = 365.45
Standard deviation of the population = 4.9 cm
Let X₁ = 360
\(Z= \frac{x-mean}{S.D}= \frac{360-365.45}{4.9}\)
Z₁ = -1.112
Let X₂ = 370
\(Z= \frac{x-mean}{S.D}= \frac{370-365.45}{4.9}\)
Z₂ = 0.911
Step(ii):-
The probability of the length of a randomly selected Cane being between 360 and 370 cm
P(x₁≤x≤x₂) = P(z₁≤Z≤z₂)
P(360 ≤X≤370) = P(-1.11≤Z≤0.911)
= P(Z≤0.911)-P(Z≤-1.11)
= 0.5 +A(0.911) - (0.5-A(1.11)
= 0.5 +A(0.911) - 0.5+A(1.11)
= A(0.911) + A(1.11)
= 0.3186 + 0.3665
= 0.6851
The probability of the length of a randomly selected Cane being between 360 and 370 cm P(360 ≤X≤370) = 0.6851
in a poll 267 students voted. nominee c received 2/3 of the votes. how many votes did nominee c receive?
Answers
Answer:
89
Step-by-step explanation:
2/3 times 267 is 178 after that you have to sub 178 from 267
what are the measurements of angles 1,2,3,4 ?

Answers
HERE IS THE ANSWER YOU WANT...
ITS COREECT....
HOPE IT HELPS YOU......
:)

Harvey is 3 times as old as Jane.The sum of their ages is 48 years. Find the age of each.
Jane is _____ years old
Harvey is ______ years old
Answers
Step-by-step explanation:
H+J=48
H=3J
3J+J=48
4J=48
From there: J=48/4
J=12
H=3J=3×12=36
Jane: 12
Harvey:36
What are the domain and range of the function f(x)= Squrt x-7+9
Answers
Answer:
domain: x ≥ 7range: f(x) ≥ 9Step-by-step explanation:
The domain is the set of values of x for which the function is defined. Those are the values of x that make the square root argument non-negative:
x -7 ≥ 0
x ≥ 7
__
Since the square root cannot be negative, the sum of it and 9 cannot be less than 9. The range is ...
f(x) ≥ 9

Answer:
domain: x ≥ 7
range: f(x) ≥ 9
Marriage Prospects Data released by the Census Bureau in 1986 indicated the likelihood that never-married women would eventually marry. The data indicated that the older the woman, the less the likelihood of marriage. Specifically, two statistics indicated that women who were 45 and never-married had an 18 percent chance of marriage and women 25 years old had a 78 percent chance of marriage. Assume that a linear fit to these two data points provides a reasonable approximation for the function p=f(a), where p equals the probability of marriage and a equals the age of a never- married woman. (a) Determine the linear function p=f(a). (b) Interpret the slope and p intercept. (c) Do the values in part b seem reasonable? (d) If the restricted domain on this function is 20 sa s 50, determine f(20), f(30), f(40), and f(50).
Answers
Answer:
See below
Step-by-step explanation:
Using the two pairs of (a, p) to determine the function:
(45, 18) and (25, 78)The function would be:
f(a) = ma + b, where m is slope, b is p-interceptSlope is:
m = (78 - 18)/(25 - 45) = -50/20 = -2.5p-intercept:
18 = -2.5*45 + bb = 18 + 112.5 = 120.5So the function is:
(a)
f(a) = -2.5a + 120.5(b) Slope is negative, indicating the lower probability at greater age. P-intercept of 120.5 is of the non-real case as for zero age it gives more than 100% probability.
(c) The domain needs restriction in line with law, so minimum age and maximum to be determined in order not to have unrealistic outcome. It should be ok between 18 and 48.
(d) The values at given points:
f(20 = -2.5*20 + 120.5 = 70.5f(30) = -2.5*30 + 120.5 = 45.5f(50) = -2.5*50 + 120.5 = -4.5 (negative probability for the age of 50 is not real)I have been failing cause of brainly i could go to a elite school but im on brainly so much i miss assignments :)
Answers
Answer:
ok dont get addicted
Step-by-step explanation:
If a circle has a radius of 12 units what is its area?
Answers
Answer: 144π units^2
Step-by-step explanation:
A=πr^2
A=π(12)^2
A=144π units^2
To solve this problem, we will visit the area of a circle formula and supply known values, such as the radius, to answer the question.
DefineTo find the area of a circle given its radius, use the formula:
\(A = \pi r ^2\)
where \(r\) is the radius of the circle and A is the area.
SubstituteSubstitute the known value for the radius in the formula.
\(A = \pi(12)^2\)
SimplifyTo simplify, use BPEMDAS, which evaluates in the proper Order of Operations:
Brackets
Parentheses
Exponents
Multiplication
Division
Addition
Subtraction
Use BPEMDAS:
\(A=\pi(144)\)
Simplify by rearranging the coefficient in front of the variable:
\(A=144\pi\)
As this is an area, our final result must be squared:
\(A=144\pi \text{ square units}\)
The final answer to this problem is \(A=144\pi\) square units. The answer can also be represented in a non-exact (approximate) format, which is solved below.
Approximate FormatTo get the non-exact format of this answer, instead of leaving \(\pi\) in the final answer, multiply it by the leading coefficient.
\(A = 144\times\pi\)
\(A= 452.38934211 ...\)
Simplify to the one-hundredths place:
\(A\approx452.39\)
For final answers:
\(\bold{Exact}: \ \boxed{A=144\pi \ \text{square units}}\)
\(\bold{Approximate}: \ \boxed{A = 452.39 \ \text{square units}}\)
To learn more about how to find the area of a circle given the radius, visit this helpful link:
https://brainly.com/question/19891555
1. (Consider the differential equationdy/dt=y(1-y^2)(i) Determine the equilibrium solutions.(ii) Obtain the general solution.(iii) Solve the initial-value problem y(0) = 1/2(iv) Draw the phase line.(v) Sketch solution curves in the ty-plane corresponding to the initial conditions y(0) =-3/2; y(0) =1/2;y(0)=3/22. Consider the differential equationDy/dt= -2ty^2.(i) Obtain the general solution.(ii) Find all values of y0 such that the solution to the initial-value problem y(-1) = y0 isdefined for all real t (i.e., find all y0 such that the solution does not blow up in finite time.)
Answers
Answer:
attached below is the detailed solution
i) equilibrium solution : y = 0 , y^2 = 1 , y = -1 , +1
ii) attached below
iii) attached below
iv) attached below
v) attached below
Step-by-step explanation:
v) For the sketch of curve attached
red curve ( y(0) ) = -3/2
blue curve ( y(0) ) = 1/2
green solution curve ( y(0) ) = 3/2

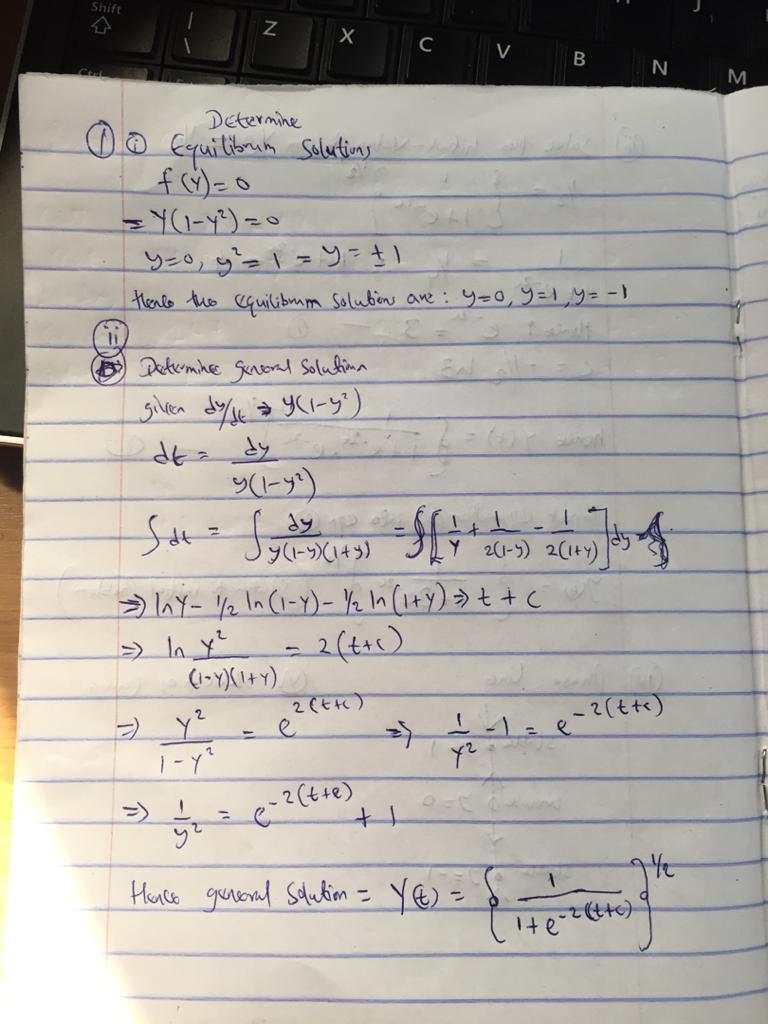

The American College Health Association produces the National College Health Assessment. The assessment indicates that the percentage of students who report having been diagnosed with depression has increased. Let’s assume that in 2010, 10% of students in one of the college campuses indicated that they had been diagnosed with depression, while in 2011, 15% of students in the same college campus indicated that they had been diagnosed with depression. The sample sizes were respectively 200 and 100.
Required:
At 0.01 level of significance, can we conclude that the proportion of college students who report having been diagnosed with depression has increased from 2010 to 2011? Make sure to state the null and the alternative hypotheses.
Answers
Answer:
No. There is not enough evidence to support the claim that the proportion of college students who report having been diagnosed with depression has increased from 2010 to 2011.
The null and alternative hypothesis are:
\(H_0: \pi_1-\pi_2=0\\\\H_a:\pi_1-\pi_2< 0\)
(Subindex 1 for 2010 and subindex 2 for 2011)
Step-by-step explanation:
This is a hypothesis test for the difference between proportions.
The claim is that the proportion of college students who report having been diagnosed with depression has increased from 2010 to 2011.
Then, the null and alternative hypothesis are:
\(H_0: \pi_1-\pi_2=0\\\\H_a:\pi_1-\pi_2< 0\)
The significance level is 0.01.
The sample 1 (2010), of size n1=200 has a proportion of p1=0.1.
The sample 2 (2011), of size n2=100 has a proportion of p2=0.15.
The difference between proportions is (p1-p2)=-0.05.
\(p_d=p_1-p_2=0.1-0.15=-0.05\)
The pooled proportion, needed to calculate the standard error, is:
\(p=\dfrac{X_1+X_2}{n_1+n_2}=\dfrac{20+15}{200+100}=\dfrac{35}{300}=0.1167\)
The estimated standard error of the difference between means is computed using the formula:
\(s_{p1-p2}=\sqrt{\dfrac{p(1-p)}{n_1}+\dfrac{p(1-p)}{n_2}}=\sqrt{\dfrac{0.1167*0.8833}{200}+\dfrac{0.1167*0.8833}{100}}\\\\\\s_{p1-p2}=\sqrt{0.0005+0.001}=\sqrt{0.0015}=0.0393\)
Then, we can calculate the z-statistic as:
\(z=\dfrac{p_d-(\pi_1-\pi_2)}{s_{p1-p2}}=\dfrac{-0.05-0}{0.0393}=\dfrac{-0.05}{0.0393}=-1.27\)
This test is a left-tailed test, so the P-value for this test is calculated as (using a z-table):
\(P-value=P(z<-1.27)=0.102\)
As the P-value (0.102) is bigger than the significance level (0.01), the effect is not significant.
The null hypothesis failed to be rejected.
There is not enough evidence to support the claim that the proportion of college students who report having been diagnosed with depression has increased from 2010 to 2011.
Among all pairs of numbers whose sum is 24, find a pair whose product is as large as possible. Show the work(the steps)! Write an equation of the corresponding quadratic function. How parabola opens? What is the maximum product? Does this function has a maximum value or the minimum value? Explain. Graph the function and upload the image.
Answers
The pair of numbers that yields the maximum product when their sum is 24 is (12, 12), and the maximum product is 144. The corresponding quadratic function is P(x) = -x^2 + 24x, and the parabola opens downwards.
To find a pair of numbers whose sum is 24 and whose product is as large as possible, we can use the concept of maximizing a quadratic function.
Let's denote the two numbers as x and y. We know that x + y = 24. We want to maximize the product xy.
To solve this problem, we can rewrite the equation x + y = 24 as y = 24 - x. Now we can express the product xy in terms of a single variable, x:
P(x) = x(24 - x)
This equation represents a quadratic function. To find the maximum value of the product, we need to determine the vertex of the parabola.
The quadratic function can be rewritten as P(x) = -x^2 + 24x. We recognize that the coefficient of x^2 is negative, which means the parabola opens downwards.
To find the vertex of the parabola, we can use the formula x = -b / (2a), where a = -1 and b = 24. Plugging in these values, we get x = -24 / (2 * -1) = 12.
Substituting the value of x into the equation y = 24 - x, we find y = 24 - 12 = 12.
So the pair of numbers that yields the maximum product is (12, 12). The maximum product is obtained by evaluating the quadratic function at the vertex: P(12) = 12(24 - 12) = 12(12) = 144.
Therefore, the maximum product is 144. This quadratic function has a maximum value because the parabola opens downwards.
To graph the function, you can plot several points and connect them to form a parabolic shape. Here is an uploaded image of the graph of the quadratic function: [Image: Parabola Graph]
For more such question on function. visit :
https://brainly.com/question/11624077
#SPJ8
which statement is true in this equation?

Answers
Answer:
B) Stan made a mistake in step one.
Step-by-step explanation:
B) Stan made a mistake in step one.
When he multiplied 8(n+20), he should have gotten 8n+160, not 8n+20.
Answer:
B
Step-by-step explanation:
He made a mistake in Step: 1
it's supposed to be
n+8n+8(20)=110
distributive property
Hope this helps :)
Write an equation of the line that is parallel to y = 1/2x + 3 and passes through the point (2,-4). A) y = 1/2x-4 - 15 B) y = -2x-4 + 15 C) y = -2x-5 D) y = 1/2x - 5
Answers
Answer:
D
Step-by-step explanation:
the equation of a line in slope- intercept form is
y = mx + c ( m is the slope and c the y- intercept )
y = \(\frac{1}{2}\) x + 3 ← is in slope- intercept form
with slope m = \(\frac{1}{2}\)
• Parallel lines have equal slopes , then
y = \(\frac{1}{2}\) x + c ← is the partial equation
to find c substitute (2, - 4 ) into the partial equation
- 4 = \(\frac{1}{2}\) (2) + c = 1 + c ( subtract 1 from both sides )
- 5 = c
y = \(\frac{1}{2}\) x - 5 ← equation of parallel line
Lesson 10 Problem Set 5•3
FONY OF UNITS
3. Darren bought some paint. He used 2 gallons painting his living room. After that, he had 3 - gallons left.
How much paint did he buy?
PLS HELP
Answers
Answer:
I think 5 gallon painting