Which statements (more than one) describe the equation 3 x 9 = 27?
3 is 27 times as many as 9.
27 is 9 times as many as 3.
9 times as many as 3 is 27.
9 times as many as 27 is 3.
3 is 9 times as many as 27
Answers
Answer:
9 times as many as 3 is 27.
Step-by-step explanation:
Related Questions
find a cartesian equation for the curve and identify it. r = 2 tan() sec()
Answers
Given the polar equation r = 2 tan θ sec θ, we need to find its cartesian equation and identify the curve it represents.To convert a polar equation to a cartesian equation,
we use the following formula:x = r cos θ, y = r sin θTherefore, r = sqrt(x² + y²) and tan θ = y/x. Also, sec θ = 1/cos θ.Hence, we can substitute these values in the given polar equation:r = 2 tan θ sec θ => r = 2 (y/x) (1/cos θ)=> r = 2y / (x cos θ) => sqrt(x² + y²) = 2y / (x cos θ) => x² + y² = (2y / cos θ)²=> x² + y² = 4y² / cos² θ=> x² + y² = 4y² (1 + tan² θ)We know that 1 + tan² θ = sec² θTherefore, x² + y² = 4y² sec² θNow, sec θ = 1/cos θ, so the cartesian equation can be written as:x² + y² = 4y² (1/cos² θ) => x² + y² = 4y² / cos² θThis equation is a circle with center (0, 0) and radius 2/cosθ. It is centered on the y-axis. Therefore, the cartesian equation for the given polar equation is x² + y² = 4y² / cos² θ, and it represents a circle centered on the y-axis.
to know more aout cartesian visit:
https://brainly.in/question/5351448
#SPJ11
The cartesian equation for the given polar equation is x² + y² = 4y² / cos² θ, and it represents a circle centered on the y-axis.
Given the polar equation r = 2 tan θ sec θ, we need to find its cartesian equation and identify the curve it represents. To convert a polar equation to a cartesian equation,
we use the following formula: x = r cos θ, y = r sin θ.
Therefore, r = √ (x² + y²) and tan θ = y/x.
Also, sec θ = 1/cos θ.
Hence, we can substitute these values in the given polar equation: r = 2 tan θ sec θ
=> r = 2 (y/x) (1/cos θ)
=> r = 2y / (x cos θ)
=> √(x² + y²) = 2y / (x cos θ)
=> x² + y² = (2y / cos θ)²
=> x² + y² = 4y² / cos² θ=>
x² + y² = 4y² (1 + tan² θ)
We know that 1 + tan² θ = sec² θ.
Therefore, x² + y² = 4y² sec² θ
Now, sec θ = 1/cos θ, so the cartesian equation can be written as:
x² + y² = 4y² (1/cos² θ) =>
x² + y² = 4y² / cos² θ
This equation is a circle with center (0, 0) and radius 2/cosθ. It is centered on the y-axis.
Therefore, the cartesian equation for the given polar equation is x² + y² = 4y² / cos² θ, and it represents a circle centered on the y-axis.
To know more about cartesian visit:
https://brainly.com/question/30637894
#SPJ11
Given: angle 1 and angle 4 form a linear pair;
angle 1 and angle 2 are supplementary
Prove: Angle 3 ~= angle 4
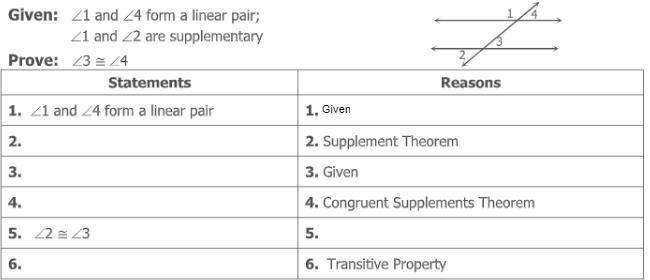
Answers
Answer:
i really hope this helps
Step-by-step explanation:
Given
angle1 + angle2 = 180
angle3 + angle4 = 180
then angle1 + angle2 = angle3 + angle4 : substitution
angle1 - angle3 = angle4 - angle2 : subtracts angle 3 and angle 2 from both sides
It has been proven that m∠3 = m∠4 . Therefore angle 3 = angle 4
From the question
angle 1 and angle 4 form a linear pair
That is,
m∠1 + m∠4 = 180° ------- (1)
Also, from the question
angle 1 and angle 2 are supplementary
That is,
m∠1 + m∠2 = 180° ------- (2)
To prove that m∠3 = m∠4
First, we can observe that
m∠2 = m∠3 (Vertically opposite angle)
From equation (2)
We have that
m∠1 + m∠2 = 180°
Since, m∠2 = m∠3
∴ m∠1 + m∠3 = 180°
Now, from equation (1)
We have
m∠1 + m∠4 = 180°
Since, m∠1 + m∠3 = 180°
Then, we can write that
m∠1 + m∠3 = m∠1 + m∠4
Subtract m∠1 from both sides
m∠1 - m∠1 + m∠3 = m∠1 - m∠1 + m∠4
∴ m∠3 = m∠4
Hence, it has been proven that m∠3 = m∠4 . Therefore angle 3 = angle 4
Learn more here: https://brainly.com/question/13805324
How many different committees of 4 students can be chosen from a group of 15?
Answers
This a case of selection because order does not matter.
The number of ways of choosing 4 from 15 is given by:
\(_{15}C_4=\frac{15\times14\times13\times12}{4!}=1365\)Therefore, the number of committees of 4 students can be chosen from a group of 15 is 1365.
.
WILL GIVE BRAINLIEST

Answers
Answer:
its 3
Step-by-step explanation:
:)can i have brainliest
Using the given right triangle, which ratio is correct?

Answers
Answer:
B
Step-by-step explanation:
Answer:
the answer is b
Step-by-step explanation:
please mark this answer as brainliest
the sscp exam consists of ____ multiple-choice questions, and must be completed within three hours.
Answers
Answer:
125 questions
Answer:
125 questions
Step-by-step explanation:
do the step by step process thank u soooooo much

Answers
Answer:
Surface area: 199.27 cm
Volume: 129.8 cm³
Step-by-step explanation:


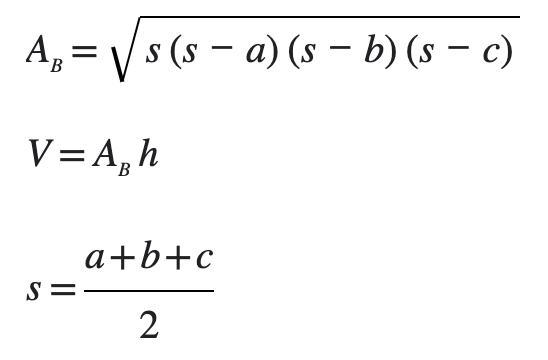

.The measures of the angles of a triangle are in the extended ratio 6: 1: 5. What is the measure of the largest angle?
Answers
9514 1404 393
Answer:
90°
Step-by-step explanation:
The largest angle is 6 of the 6+1+5 = 12 ratio units, so is 6/12 = 1/2 of the total number of degrees in a triangle.
The largest angle is 1/2(180°) = 90°.
. let ???? be a discrete random variable that is uniformly distributed over the set of integers in the range [????, ????], where ???? and ???? are integers with ???? < 0 < ????. find the pmf of the random variables max(0,????) and min(0,????).
Answers
Filling in the blanks, I assume you're talking about a random variable \(X\) distributed uniformly over the integers \(a\le x\le b\). Let both \(a,b>0\) so we can write the support of \(X\) as the set
\(S = \{-a, -a+1, -a+2, \ldots, -1, 0, 1, \ldots, b-2, b-1, b\}\)
Note that \(|S| = a+b+1\), so the PMF of \(X\) is
\(\mathrm{Pr}(X=x) = \begin{cases}\frac1{a+b+1} & \text{if } x\in S \\ 0 & \text{otherwise}\end{cases}\)
Let \(Y=\max\{0,X\}\). Then
\(Y = \max\{0,X\} = \begin{cases}0 & \text{if } X\le0 \\ X & \text{if } X>0 \end{cases}\)
which tells us
\(\displaystyle \mathrm{Pr}(Y=0) = \mathrm{Pr}(X\le0) = \sum_{x=-a}^0 \mathrm{Pr}(X=x) = \frac{a+1}{a+b+1}\)
and
\(\displaystyle \mathrm{Pr}(Y\neq0) = \mathrm{Pr}(X>0) = \sum_{x=1}^b \mathrm{Pr}(X=x) = \frac b{a+b+1}\)
Hence the PMF of \(Y\) is
\(\mathrm{Pr}(Y=y) = \begin{cases}\frac{a+1}{a+b+1} & \text{if } y=0 \\\\ \frac b{a+b+1} & \text{otherwise}\end{cases}\)
Let \(Z=\min\{0,X\}\). The same reasoning applies, but this time
\(Z = \min\{0,X\} = \begin{cases} 0 & \text{if } X \ge 0 \\ X & \text{if } X < 0 \end{cases}\)
Now
\(\displaystyle \mathrm{Pr}(Z=0) = \mathrm{Pr}(X\ge0) = \sum_{x=0}^b \mathrm{Pr}(X=x) = \frac{b+1}{a+b+1}\)
and
\(\displaystyle \mathrm{Pr}(Z\neq0) = \mathrm{Pr}(X<0) = \sum_{x=-a}^{-1} \mathrm{Pr}(X=x) = \frac a{a+b+1}\)
so that
\(\mathrm{Pr}(Z=z) = \begin{cases}\frac{b+1}{a+b+1} &\text{if }z=0 \\\\ \frac a{a+b+1} & \text{otherwise}\end{cases}\)
Write a factor that you can use to rationalize the denominator of √2/√5−8.
Answers
Write a factor that you can use to rationalize the denominator of √2/√5−8.
Answer: √5+8
What is true as the spread of scores around the arithmetic mean gets smaller? A. The coefficient of variation gets smaller B. The interquartile range gets smaller. C. The standard deviation gets smaller D. All of the above
Answers
The correct answer is D. All of the above. When the spread of scores around the arithmetic mean gets smaller, it means that the data points are closer to the mean.
This has several implications:
A. The coefficient of variation (CV) gets smaller: The coefficient of variation is the ratio of the standard deviation to the mean. When the standard deviation decreases (due to smaller spread of scores), the CV also decreases.
B. The interquartile range (IQR) gets smaller: The IQR represents the range between the first quartile and the third quartile. When the spread of scores decreases, the values at the first and third quartiles are closer together, resulting in a smaller IQR.
C. The standard deviation gets smaller: The standard deviation measures the average distance of data points from the mean. As the spread of scores decreases, the data points are closer to the mean, resulting in a smaller standard deviation.
In summary, when the spread of scores around the arithmetic mean gets smaller, the coefficient of variation, interquartile range, and standard deviation all decrease.
To know more about the arithmetic mean, visit:
https://brainly.com/question/29445117
#SPJ11
the ratio of dividends to the average number of common shares outstanding is:
Answers
The ratio of dividends to the average number of common shares outstanding is known as the dividend yield. It is a measure of the return on an investment in the form of dividends received relative to the number of shares held.
To calculate the dividend yield, you need to divide the annual dividends per share by the average number of common shares outstanding during a specific period. The annual dividends per share can be obtained by dividing the total dividends paid by the number of outstanding shares. The average number of common shares outstanding can be calculated by adding the beginning and ending shares outstanding and dividing by 2.
For example, let's say a company paid total dividends of $10,000 and had 1,000 common shares outstanding at the beginning of the year and 1,500 shares at the end. The average number of common shares outstanding would be (1,000 + 1,500) / 2 = 1,250. If the annual dividends per share is $2, the dividend yield would be $2 / 1,250 = 0.0016 or 0.16%.
In summary, the ratio of dividends to the average number of common shares outstanding is the dividend yield, which measures the return on an investment in terms of dividends received per share held.
To know more about dividend, here
brainly.com/question/3161471
#SPJ11
2. 6. 4 practice algebra 2 you are helping to design a road for a high mountain pass. There are two routes over the pass, but both have to cross step ravines. Use what you know about solving radical functions to design a bridge that will safely cross the ravine
Answers
Answer:
Step-by-step explanation:
I can provide you with general information about radical functions and their graphs, but I cannot design a bridge for you.
In order to design a bridge that will safely cross the ravine, you would need to take into account a wide range of factors, including the length and width of the ravine, the types of materials that can be used to construct the bridge, the weight and size of the vehicles that will be crossing the bridge, and the weather and environmental conditions in the area. This would likely require the expertise of a civil engineer or other trained professional.
Regarding radical functions, they are functions that involve a radical symbol (such as a square root) in their equation. The graph of a radical function is typically a curve that starts at the point (0,0) and moves upwards and to the right. The shape of the curve will depend on the specific radical function and the values of its parameters.
To solve a radical function, you would typically isolate the radical term on one side of the equation and then square both sides of the equation to eliminate the radical. However, it is important to be careful when squaring both sides, as this can introduce extraneous solutions that do not satisfy the original equation.
Can someone please help me?

Answers
9514 1404 393
Answer:
d
Step-by-step explanation:
The geometric sequence is ...
20, 10, 5
so has a common ratio of 10/20 = 5/10 = 1/2.
Only one answer choice shows that each successive term is 1/2 the one before. That is choice D.

Need help???!!!! Please

Answers
This is because
3*2 = 6 up top3+2 = 5 down belowThis is found through trial and error.
This is for problem 1 only. Problems 2 through 6 will follow a similar structure.
what is a type i error?when we reject the null hypothesis, but it is actually truewhen we fail to reject the null hypothesis, but it is actually falsewhen we reject the null hypothesis and it is false
Answers
A level of 0.05 is used, which means that there is a 5% chance of making a type I error.
A type I error occurs when we reject the null hypothesis, but it is actually true. This means that we have made a mistake in concluding that there is a significant difference between two groups or variables, when in fact there is not. This can happen due to factors such as sample size, random variability or bias.
For example, if a drug company tests a new medication and concludes that it is effective in treating a certain condition, but in reality it is not, this would be a type I error. This could lead to the medication being approved and prescribed to patients, which could potentially harm them and waste resources.
In statistical analysis, a type I error is represented by the significance level, or alpha level, which is the probability of rejecting the null hypothesis when it is actually true. It is important to set a reasonable alpha level to minimize the risk of making a type I error. Generally, a level of 0.05 is used, which means that there is a 5% chance of making a type I error.
Learn more about hypothesis brainly.com/question/30899146
#SPJ11
Evaluate expressions-
If x=3 what is the value of 8x+23?
A.47
B.93
C.208
D.61
Answers
Explanation:
We replace x with 3 and use PEMDAS to evaluate
8*x+23
8*3+23
24+23
47
Answer:
\(47\)
Step-by-step explanation:
\(8x + 23\)
\(8(3) + 23\)
\(24 + 23\)
\(47\)
Hope it is helpful...devi bought 7 skirts at x$ each n skirts at 12$ each 2n +1 at 15 each a nd 4 skirts at $3x find the total
Answers
Answer:
$(19x + 42n + 15)
Step-by-step explanation:
Devi bought 7 skirts at $x each, n skirts at $12 each, (2n + 1) skirts at $15 each and 4 skirts at $3x each. Find the total cost of the skirts she bought.
total cost of the skirt bought can be determined by adding the total costs of each shirt bought
7 skirts at $x each = $7x
n skirts at $12 each = $12n
(2n + 1) skirts at $15 = (2n + 1) x 15 = 30n + 15
4 skirts at $3x each = $12x
7x + 12n + 30n + 15 + 12x
combine like terms
19x + 42n + 15
Rebecca's boss pays her time and a half for overtime work at the comic book store. If her regular wage is $8.50, what is Rebecca paid for overtime work?
Answers
The amount that Rebecca will be paid for overtime work is $12.75.
How to calculate the value?From the information, Rebecca's boss pays her time and a half for overtime work at the comic book store. Her regular wage is $8.50.
The amount for overtime will be:
= (1.5 × $8.50)
= $12.75
Therefore, the amount that Rebecca will be paid for overtime work is $12.75.
Learn more about pay on:
brainly.com/question/15530787
#SPJ1
Indicate whether or not the following signals are periodic, and if so find their periods. a) x[n] = e²+j5n b) x (t) = sin¹ (70m t) c) x[n] = cos(0.375n n) + sin(0.5π n)
Answers
a) x[n] = e²+j5n is not periodic.
b) x(t) = sin¹ (70m t) has a period of T = 2π / (70m).
c) x[n] = cos(0.375n) + sin(0.5π n) has a period of T = 8.
To determine if the given signals are periodic, we need to check if there exists a positive value T for which the signals repeat after every T units of time (for continuous-time signals) or every T samples (for discrete-time signals). Let's analyze each signal:
a) x[n] = e²+j5n
This discrete-time signal is not periodic. The exponential term e² will keep growing as n increases, and there is no repeating pattern.
b) x(t) = sin¹ (70m t)
This continuous-time signal is periodic. To find its period, we need to identify the smallest positive value T for which sin¹ (70m t) repeats. The period of a sin¹ function is 2π, divided by the coefficient of t inside the sin¹ function. Therefore, the period is T = 2π / (70m).
c) x[n] = cos(0.375n) + sin(0.5π n)
This discrete-time signal is periodic. To find its period, we need to identify the smallest positive value T for which cos(0.375n) and sin(0.5π n) repeat. The period of both cos and sin functions is 2π. We need to find the least common multiple (LCM) of the coefficients in front of n for both terms, which is 8. Therefore, the period is T = 8.
To learn more about periodic here:
https://brainly.com/question/28223229
#SPJ4
The function f(x) = 4x + 10 models the amount of money francis makes when babysitting for x hours. How much money will he make for 2 hours of babysitting work?.
Answers
The amount of money that he will make for 2 hours of baby sitting work is $18
The function is
f(x) = 4x + 10
The function f(x) is the amount of money Francis makes when babysitting for x hours
The function is the mathematical statement that shows the relationship between one variable and another variable. If one variable is dependent variable then the other variable will independent variable
The function
f(x) = 4x + 10
The number of hours x = 2 hours
Substitute the values of x in the function
f(2) = 4(2) + 10
f(2) = 8 +10
f(2) = $18
Hence, the amount of money that he will make for 2 hours of baby sitting work is $18
Learn more about function here
brainly.com/question/20534410
#SPJ4
what is 9.4 rounded to the nearest tenth?
Answers
Answer: the answer is going to be 9
Answer:
9.4 rounded to the nearest 10th - 9
Step-by-step explanation:
If the tenth in the decimal is 4 or lower, (like 9.4 or 9.3) It would round down to 9, but if it were 5 or higher like (9.5) it would be 10.00 or 10 :)
What is the equation of the horizontal asymptote for the following exponential graph? Please help I need it

Answers
Answer:
y=5
Step-by-step explanation:
The curve stops at the y value of 6. And we need a horizontal line for the asymptote, so we don't need an x value only a y-value. So the y-value is 5 on the y-axis, which means your equation will be y=5.
-Hope this helped
there are 3 numbers in ascending order such that the difference of first two is 10 and that of last two is 12. if the sum of three numbers is 47, find the least number.
Answers
Answer:
17/3
Step-by-step explanation:
x + y + z = 47
y - x = 10 x = y - 10
z - y = 10 z = 10 + y
y-10 + y + 10 + y = 47
3 y = 47
y = 47/3 x = 17/3 z = 77/3
Answer:
5
Step-by-step explanation:

Two long thin parallel wires 13.0 cm apart carry 25-A currents in the same direction.
Part A
Determine the magnitude of the magnetic field vector at a point 10.0 cm from one wire and 6.0 cm from the other (Figure 1) .
Express your answer using two significant figures. B=?
Part B
Determine the direction of the magnetic field vector at that point.
Express your answer using two significant figures.
Answers
The magnitude of the magnetic field at that point is 3.08 × 10^-5 T.
The magnitude of the magnetic field can be calculated using Ampere's Law. The formula is given by:
B = (μ₀ * I) / (2 * π * r)
where B is the magnetic field, μ₀ is the permeability of free space (4π * 10^-7 T·m/A), I is the current, and r is the distance from the wire.
Calculating the magnetic field for each wire separately and adding them together:
B₁ = (4π * 10^-7 T·m/A * 25 A) / (2 * π * 0.10 m) = 1.0 × 10^-5 T
B₂ = (4π * 10^-7 T·m/A * 25 A) / (2 * π * 0.06 m) = 2.08 × 10^-5 T
The total magnetic field at that point is the sum of the individual magnetic fields:
B = B₁ + B₂ = 1.0 × 10^-5 T + 2.08 × 10^-5 T = 3.08 × 10^-5 T
Therefore, the magnitude of the magnetic field at that point is 3.08 × 10^-5 T.
To know more about Ampere's Law refer here:
https://brainly.com/question/31377741
#SPJ11
There is a narrow rectangular plot, reserved for a school, in Mahuli VIIage
length and breadth of the plot are in the ratio 11:4. At the rate 100 per metre it will
cost the village panchayat 75000 to fence the plot. What are the dimensions of
the plot?
Answers
Answer:
550x100
Step-by-step explanation:
First divide 75000 by 100 to get 750. Then divide 750 by 15 to get 50. Lastly multiply 50 by 11 to get 550 and multiply 50 by 4 to get 100.
) DF and GI are parallel lines. D G C E H F Which angles are alternate exterior angles?
Answers
<IHE and <DEH are alternate interior angles.
We know, Alternate interior angles are a pair of angles that are formed on opposite sides of a transversal and are located between the lines being intersected. These angles are congruent or equal in measure.
In other words, if two parallel lines are intersected by a transversal, the alternate interior angles will have the same measure. They are called "alternate" because they are located on alternate sides of the transversal.
Since, DF || GI then
angle GHJ and angle DEC - Angle on same side
angle FEH and angle IHJ - Corresponding Angle
angle IHJ and angle FEC - Angle on same side
angle IHE and angle DEH - Alternate interior angle
Learn more about Alternate interior angle here:
https://brainly.com/question/29114209
#SPJ1
The Complete question is:
Which angles are alternate interior angles?
angle GHJ and angle DEC
angle FEH and angle IHJ
angle IHJ and angle FEC
angle IHE and angle DEH
Una autopista atraviesa un cerro mediante un túnel que tiene forma de arco parabólico, tiene 4 metros de altura ¿Cuál es la altura máxima que puede tener un camión de transporte que tiene 2 metros de ancho para pasar sin atorarse?
Answers
Answer:
supongo que < 3m
Step-by-step explanation:
el túnel tiene forma de arco parabólico, pero no aclara qué coeficiente tiene el término \(x^{2}\), ej: si es -\(x^{2}\), ó -0.5 \(x^{2}\), ó -0.1 \(x^{2}\), ...
Suponiendo que tuviese coeficiente -1, entonces la ecuación del puente es:
f(x) = -\(x^{2}\) + 4
Tomamos el valor de f(x=1) = f(x=-1), porque suponiendo que el camión va por el centro del túnel, y teniendo 2m de ancho, queda 1m hacia cada lado:
f(x=1) = f(x=-1) = 3
Con lo cual si el camión tiene 3m de alto choca con la curva parabólica que forma el túnel.

plz help yall ;-; I need this by tonight

Answers
x^154
54b^20
step by step
Use the definition of Taylor series to find the Taylor series (centered at c ) for the function. f(x)=e 4x
,c=0 f(x)=∑ n=0
[infinity]
Answers
The answer is , the Taylor series (centered at c=0) for the function f(x) = e^(4x) is given by:
\($$\large f(x) = \sum_{n=0}^{\infty} \frac{4^n}{n!}x^n$$\)
The Taylor series expansion is a way to represent a function as an infinite sum of terms that depend on the function's derivatives.
The Taylor series of a function f(x) centered at c is given by the formula:
\(\large f(x) = \sum_{n=0}^{\infty} \frac{f^{(n)}(c)}{n!}(x-c)^n\)
Using the definition of Taylor series to find the Taylor series (centered at c=0) for the function f(x) = e^(4x), we have:
\(\large e^{4x} = \sum_{n=0}^{\infty} \frac{e^{4(0)}}{n!}(x-0)^n\)
\(\large e^{4x} = \sum_{n=0}^{\infty} \frac{4^n}{n!}x^n\)
Therefore, the Taylor series (centered at c=0) for the function f(x) = e^(4x) is given by:
\($$\large f(x) = \sum_{n=0}^{\infty} \frac{4^n}{n!}x^n$$\)
To know more about Function visit:
https://brainly.in/question/222093
#SPJ11
The Taylor series for f(x) = e^(4x) centered at c = 0 is:
f(x) = 1 + 4x + 8x^2 + 32x^3/3 + ...
To find the Taylor series for the function f(x) = e^(4x) centered at c = 0, we can use the definition of the Taylor series. The general formula for the Taylor series expansion of a function f(x) centered at c is given by:
f(x) = f(c) + f'(c)(x - c) + f''(c)(x - c)^2/2! + f'''(c)(x - c)^3/3! + ...
First, let's find the derivatives of f(x) = e^(4x):
f'(x) = d/dx(e^(4x)) = 4e^(4x)
f''(x) = d^2/dx^2(e^(4x)) = 16e^(4x)
f'''(x) = d^3/dx^3(e^(4x)) = 64e^(4x)
Now, let's evaluate these derivatives at x = c = 0:
f(0) = e^(4*0) = e^0 = 1
f'(0) = 4e^(4*0) = 4e^0 = 4
f''(0) = 16e^(4*0) = 16e^0 = 16
f'''(0) = 64e^(4*0) = 64e^0 = 64
Now we can write the Taylor series expansion:
f(x) = f(0) + f'(0)(x - 0) + f''(0)(x - 0)^2/2! + f'''(0)(x - 0)^3/3! + ...
Substituting the values we found:
f(x) = 1 + 4x + 16x^2/2! + 64x^3/3! + ...
Simplifying the terms:
f(x) = 1 + 4x + 8x^2 + 32x^3/3 + ...
Therefore, the Taylor series for f(x) = e^(4x) centered at c = 0 is:
f(x) = 1 + 4x + 8x^2 + 32x^3/3 + ...
To know more about Taylor series, visit:
https://brainly.com/question/32235538
#SPJ11