Which shows the equation below written in the form ax2 + bx + c = 0?
x + 9 = 4(x-1)^2
LOOK AT THE PICTURE REALLY EASY

Answers
Answer:
D
Step-by-step explanation:
We have the equation:
\(x+9=4(x-1)^2\)
To convert this to standard form, we can simply expand.
First, expand the right-hand side:
\(x+9=4(x^2-2x+1)\)
Distribute the right:
\(x+9=4x^2-8x+4\)
Subtract 9 from both sides:
\(x=4x^2-8x-5\)
Finally, subtract an x from both sides:
\(0=4x^2-9x-5\)
Flip:
\(4x^2-9x-5=0\)
Hence, our answer is D.
Related Questions
Add the polynomials :)

Answers
Answer:
4x^3+6x^2-15x+6
Step-by-step explanation:
Answer:
\(4x^2 + 6x^2 - 15x + 5\)
Step-by-step explanation:
Hello!
We can add like terms.
The terms that we see here are \(x^3, x^2, x,\) and integer values.
We can combine like terms by adding the coefficients.
Add\((6x^2 - 9x + 6)+(4x^3 - 6x)\)\(6x^2 - 9x + 6 + 4x^3 - 6x\)\(4x^3 + 6x^2 - 9x - 6x + 6\)\(4x^2 + 6x^2 - 15x + 5\)Order: Highest degree to lowest degree. The final expression is \(4x^2 + 6x^2 - 15x + 5\)
In triangle ABC, ACB = 67°, AB= 6.9 cm and
BC = 5.7 cm.
a Calculate angle BÂC.
b Hence find the area of AABC.
Please answer all questions to 3 correct sig figs.
Answers
Answer:
In triangle ABC, ACB = 67°, AB= 6.9 cm and BC = 5.7 cm.
Step-by-step explanation:
Help please
ху
22
34
46
58
Which function corresponds with the table?

Answers
backtracking with conflict-directed back-jumping, where the variable order is (a1, h, a4, f1, a2, f2, a3, t), and the value order is (red, green, blue)
Answers
In backtracking with conflict-directed back-jumping, the search for a solution to a problem is performed using a depth-first search algorithm. The variable order you mentioned, (a1, h, a4, f1, a2, f2, a3, t), represents the sequence in which variables are assigned values during the search. The value order, (red, green, blue), indicates the order in which the algorithm will try assigning different values to the variables.
Conflict-directed back-jumping is an improvement over basic backtracking, as it helps reduce the search space by identifying and jumping over irrelevant parts of the search tree. When a conflict (i.e., an unsolvable assignment) is encountered, the algorithm doesn't simply backtrack to the previous variable but rather identifies the cause of the conflict and jumps back to the most recent variable responsible for the conflict. This allows the algorithm to skip parts of the search tree that are guaranteed not to yield a solution.
In summary, backtracking with conflict-directed back-jumping is an efficient search technique that uses a specific variable and value order to assign values during the search. It improves upon basic backtracking by identifying the cause of conflicts and jumping back to the most recent relevant variable, thus reducing the search space and time complexity.
for such more questions on algorithms
https://brainly.com/question/13800096
#SPJ11
Central conservative forces: (a) Consider the force F= r2kr^ : Is this force conservative? Is it central? If it is conservative find the potential energy V(r). For full marks you need to justify your answer and explain any assumptions that you make.
Answers
The force F = r^2k(r^) is not conservative because its curl is nonzero. The force is central because it depends only on r and acts along the radial direction. Since it is not conservative, there is no potential energy function V(r) associated with this force
To determine whether the force F = r^2k(r^) is conservative and central, let's analyze its properties.
A force is conservative if it satisfies the condition ∇ × F = 0, where ∇ is the gradient operator. In Cartesian coordinates, the force can be written as F = Fx i + Fy j + Fz k, where Fx, Fy, and Fz are the components of the force in the x, y, and z directions, respectively. The curl of F is given by:
∇ × F = (∂Fz/∂y - ∂Fy/∂z)i + (∂Fx/∂z - ∂Fz/∂x)j + (∂Fy/∂x - ∂Fx/∂y)k.
Calculating the components of F = r^2k(r^):
Fx = 0, since there is no force component in the x-direction.
Fy = 0, since there is no force component in the y-direction.
Fz = r^2kr^.
Taking the partial derivatives, we have:
∂Fz/∂x = ∂/∂x (r^2kr^) = 2rkr^2(∂r/∂x) = 2rkr^2(x/r) = 2xkr^3.
∂Fz/∂y = ∂/∂y (r^2kr^) = 2rkr^2(∂r/∂y) = 2rkr^2(y/r) = 2ykr^3.
Substituting these values into the curl equation, we get:
∇ × F = (2ykr^3 - 2xkr^3)k = 2k(r^3y - r^3x).
Since the curl of F is not zero, ∇ × F ≠ 0, we conclude that the force F = r^2k(r^) is not conservative.
Now let's determine if the force is central. A force is central if it depends only on the distance from the origin (r) and acts along the radial direction (r^).
For F = r^2k(r^), the force is indeed central because it depends solely on r (the magnitude of the position vector) and acts along the radial direction r^. Hence, it can be written as F = Fr(r^), where Fr is a function of r.
Since the force is not conservative, it does not possess a potential energy function. In conservative forces, the potential energy function V(r) can be defined, and the force can be expressed as the negative gradient of the potential energy, i.e., F = -∇V. However, since F is not conservative, there is no potential energy function associated with it.
Learn more about force from this link:
https://brainly.com/question/12785175
#SPJ11
How many 5-digit palindromes contain only even digits?
Answers
Answer:
400
Step-by-step explanation:
There are 400.
Assuming the number must be at least 10,000, then:
In a 5 digit palindrome, the first and last digits must be the same, and the second and fourth digits must be the same; and:
For the first and last digit there is a choice of 4 digits {2, 4, 6, 8};
For each of these there is a choice of 10 digits {0, 1, ..., 9} for the second and fourth digits;
For each of the above choices these is a choice of 10 digits {0, 1, ..., 9} for the third digit;
Making 4 x 10 x 10 = 400 possible even 5 digit palindromes.
What weight is shown?
0
500
grams

Answers
Answer:
The answer is 175 grams
Step-by-step explanation:
100 than 150, its close to 175 if u estimate
Kenya is touring a chocolate factory, and she has seen 15%, or 24,000 square
feet, so far. She will see the other 85% of the factory tomorrow. How many
square feet are there in the remaining 85% of the factory?
Answers
Answer: 136,000
Step-by-step explanation:
To find the number of square feet in the remaining 85% of the chocolate factory, we'll first calculate the total square footage of the factory.
We know that Kenya has seen 15% of the factory, which corresponds to 24,000 square feet. Let's represent the total square footage of the factory as "T."
We can set up the following equation based on the given information:
15% of T = 24,000 square feet
Mathematically, this equation can be written as:
0.15T = 24,000
To find the total square footage (T), we can divide both sides of the equation by 0.15:
T = 24,000 / 0.15
T = 160,000 square feet
Now, to find the square footage of the remaining 85% of the factory, we'll calculate 85% of the total square footage:
85% of T = 0.85 * T
= 0.85 * 160,000
= 136,000 square feet
Therefore, there are 136,000 square feet in the remaining 85% of the chocolate factory.
What is the domain of the exponential function f(x) = 3 ^ x - 5
Answers
Answer:
(-infinity, infinity)
Step-by-step explanation:
The domain of the exponential function f(x) = 3 ^ x - 5 is (-infinity, infinity)
What is the exponential function?An exponential function is a mathematical function of the following form: f ( x ) = an x. where x is a variable, and a is a constant called the base of the function. The most commonly encountered exponential-function base is the transcendental number e, which is equal to approximately 2.71828.
What is the exponential function formula?Exponential Function Formula
An exponential function is defined by the formula f(x) = ax, where the input variable x occurs as an exponent. The exponential curve depends on the exponential function and it depends on the value of the x.
Learn more about Exponential Function at https://brainly.com/question/12940982
#SPJ2
PLS HELP ASAP 100 POINTS
Find the measure of ∠YOZ by answering the questions.
1. Find the measure of ∠WOV. Which angle relationship did you use? (3 points)
2. Now find the measure of ∠YOZ. Which angle relationship did you use?
3. Check your answer by using another strategy to find the measure of ∠YOZ. Describe your strategy, and show that it gives the same measure for ∠YOZ. (4 points)

Answers
Answer:
60°60°, vertical angles60°, measure of a straight angleStep-by-step explanation:
Given right angle XOV and 30° angle XOW, you want to know the measure of angle WOV. You also want to find the measure of angle YOZ, which is opposite angle VOW, where XOY is a right angle, and WOZ is a straight angle.
1. WOVThe angle addition theorem tells you that ...
∠XOW +∠WOV = ∠XOV
Angle XOV is given as a right angle, and angle XOW is shown as 30°, so we have ...
30° +∠WOV = 90°
∠WOV = 60° . . . . . . . . . subtract 30° from both sides
Angle WOV is 60° using the angle addition theorem.
2. YOZRays OY and OV are opposite rays, as are rays OZ and OW. This means angles YOZ and VOW are vertical angles, hence congruent.
∠YOZ = ∠WOV = 60°
Angle YOZ is 60° using the congruence of vertical angles.
3. YOZ another wayAs in part 2, angle WOZ is a straight angle, so measures 180°. The angle addition theorem tells you this is the sum of its parts:
∠ZOY +∠YOX +∠XOW = ∠ZOW
∠ZOY +90° +30° = 180°
∠ZOY = 60° . . . . . . . . . . . . . subtract 120° from both sides
Angle YOZ is 60° using the measure of a straight angle.
<95141404393>
Assign "smallest" to the smallest number of students they should sample to ensure that a 95% confidence interval for the parameter has a width of no more than 6 from left end to right end.
a) 36
b) 72
c) 144
d) 288
Answers
To determine the smallest number of students required to ensure a 95% confidence interval with a width of no more than 6, we need to calculate the sample size using the formula:
n = (Z * σ / E)^2
Where:
n = sample size
Z = Z-score corresponding to the desired confidence level (95% confidence level corresponds to a Z-score of approximately 1.96)
σ = standard deviation of the population (unknown in this case)
E = maximum margin of error (half the desired width of the confidence interval, which is 6/2 = 3)
Using the provided options, we can calculate the sample size for each:
a) n = (1.96 * σ / 3)^2 = (1.96/3)^2 ≈ 1.29
b) n = (1.96 * σ / 3)^2 = (1.96/3)^2 ≈ 1.29
c) n = (1.96 * σ / 3)^2 = (1.96/3)^2 ≈ 1.29
d) n = (1.96 * σ / 3)^2 = (1.96/3)^2 ≈ 1.29
As you can see, the sample size calculation does not depend on the provided options. The resulting value is approximately 1.29, which is not a whole number. Therefore, none of the given options are correct.
To know more about value visit-
brainly.com/question/28640311
#SPJ11
1. 14 is what percent of 56? 2. 110% of 90 is what number?
3. 38 is 40% of what number? 4. 13 is what percent of 65?
5. 2% of 200 is what number? 6. 1/2 is 25% of what number?
7. A restaurant raises its prices by 10% to account for the rising prices of supplies and ingredients. The restaurant’s signature pasta dish costs $14 before the price increase. What is the new price of the pasta dish?
Solve this problem using an equation or expression.
Mariam solves this problem by finding 110% of $14. Explain why Mariam’s strategy is correct. How does this strategy compare to yours?
Answers
Answer:
Due to the general stability of Egyptian life and culture, all arts - including architecture and sculpture, as well as painting, metalwork and goldsmithing - were characterized by a highly conservative adherence to traditional rules, which favoured order and form over creativity and artistic expression
A triangle has two sides measuring 8. 5 cm and 15 cm. What are the least and greatest whole number possibilities for the third side? enter your answers in the boxes.
Answers
The least whole number possibility for the third side is 8 cm. The greatest whole number possibility for the third side is 22 cm.
A triangle is a three-sided polygon. It is a geometric shape that has three edges and three vertices. Triangles can be classified based on their side lengths (such as equilateral, isosceles, or scalene) or based on the angles between their sides (such as acute, right, or obtuse). Triangles are a fundamental shape in geometry and are used in many branches of mathematics and physics. To form a triangle, the sum of the lengths of any two sides must be greater than the length of the third side.
Using this rule, we can find the possible range of values for the third side of the triangle.
The least possible length of the third side would be:
8.5cm + 15cm - 15cm = 8.5cm
The greatest possible length of the third side would be:
(8.5cm + 15cm) - 1cm = 22.5cm
Learn more about triangle, here https://brainly.com/question/2773823
#SPJ4
Find the measure of

Answers
Answer:
12
Step-by-step explanation:
See attachment for step-by-step instructions
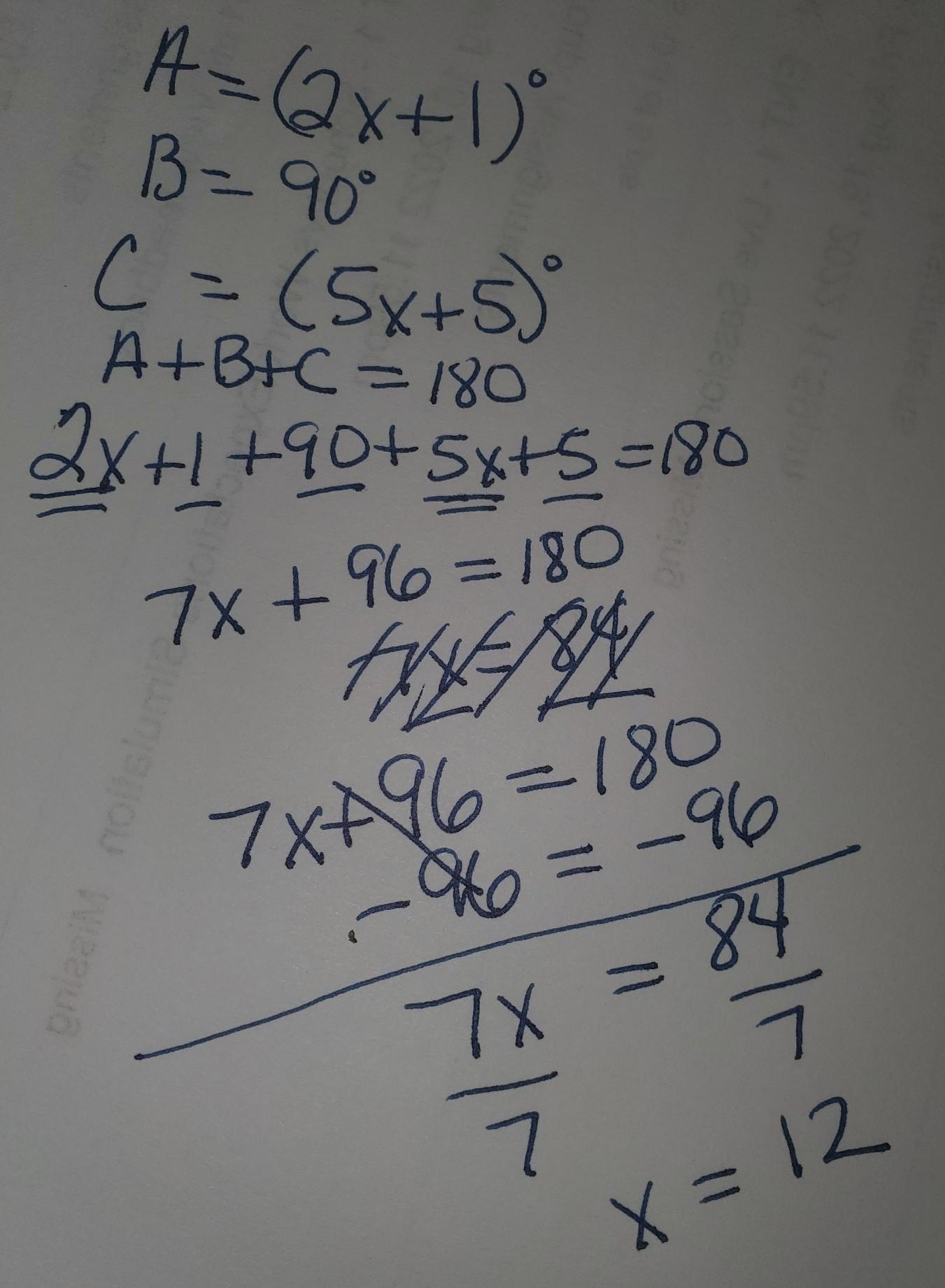
Let P(n) be the equation: 11⋅2+12⋅3+⋅⋅⋅+1n⋅(n+1)=nn+1 for all the natural numbers n≥1.
A mathematical induction proof consists of two steps: the basis step and the inductive step. Answer the following questions: Show the equation is true in the basis step. What is the equation of the inductive hypothesis (IH)? You don't need to show the equation is true. What is the equation we need to show in the inductive step?
Answers
In the basis step of the mathematical induction proof for P(n), we show that the equation is true for n = 1. The equation of the inductive hypothesis (IH) is P(k), where k is an arbitrary natural number. In the inductive step, we need to show that if P(k) is true, then P(k+1) is also true.
In the basis step, we substitute n = 1 into the equation 11⋅2+12⋅3+⋅⋅⋅+1n⋅(n+1)=nn+1. This gives us the equation 1⋅2 = 1+1, which is true.
The inductive hypothesis (IH) is denoted as P(k), where k is an arbitrary natural number. We assume that P(k) is true, meaning that 11⋅2+12⋅3+⋅⋅⋅+1k⋅(k+1)=kk+1 holds.
In the inductive step, we need to show that if P(k) is true, then P(k+1) is also true. This involves substituting n = k+1 into the equation 11⋅2+12⋅3+⋅⋅⋅+1n⋅(n+1)=nn+1 and demonstrating that the equation holds for this value. The specific equation we need to show in the inductive step is 11⋅2+12⋅3+⋅⋅⋅+1(k+1)⋅((k+1)+1)=(k+1)(k+1+1).
Learn more about inductive hypothesis here: brainly.com/question/31703254
#SPJ11
In the basis step, we need to show that the equation P(1) is true. The equation of the inductive hypothesis (IH) is P(k), where k is any natural number greater than or equal to 1. In the inductive step, we need to show that if P(k) is true, then P(k+1) is also true.
To prove the equation P(n): 11⋅2 + 12⋅3 + ... + 1n⋅(n+1) = n(n+1) using mathematical induction, we follow the two-step process.
1. Basis Step:
We start by showing that the equation is true for the base case, which is n = 1:
P(1): 11⋅2 = 1(1+1)
Simplifying, we get: 2 = 2, which is true.
2. Inductive Step:
Assuming that the equation is true for some arbitrary value k, the inductive hypothesis (IH) is:
P(k): 11⋅2 + 12⋅3 + ... + 1k⋅(k+1) = k(k+1)
In the inductive step, we need to show that if P(k) is true, then P(k+1) is also true:
P(k+1): 11⋅2 + 12⋅3 + ... + 1k⋅(k+1) + 1(k+1)⋅((k+1)+1) = (k+1)((k+1)+1)
By adding the (k+1)th term to the sum on the left side and simplifying the right side, we can demonstrate that P(k+1) is true.
Learn more about equation here: brainly.com/question/30130739
#SPJ11
Pls Help! John wants to prove ABC = to DEF. He Knoes AB = DE and AC = DF. With Screenshot

Answers
Answer:
\( \angle A \cong \angle D \)
Step-by-step explanation:
The Side-Angle-Side method cana only be used when information given shows that an included angle which is between two sides of a ∆, as well as the two sides of the ∆ are congruent to the included side and two sides of the other ∆.
Thus, since John already knows that \( \overline{AB} \cong \overline{DE} \) and \( \overline{AC} \cong \overline{DF} \), therefore, an additional information showing that the angle between \( \overline{AB} \) and \( \overline{DE} \) in ∆ABC is congruent to the angle between \( \overline{AC} \) and \( \overline{DF} \) in ∆DEF.
For John to prove that ∆ABC is congruent to ∆DEF using the Side-Angle-Side method, the additional information needed would be \( \angle A \cong \angle D \).
See attachment for the diagram that has been drawn with the necessary information needed for John to prove that ∆ABC is congruent to ∆DEF.

URGENT
Which of the following is the maximum value of the function y = -x²+2x+1?
1
-1
2
0
Answers
The maximum value of the function is 2.
How to find the maximum value of a quadratic function?
The maximum value of a quadratic function y = ax² + bx + c is given by the formula:
y (max) = c - b²/4a
We have the function, y = -x²+2x+1
where a = -1, b = 2 and c = 1
y (max) = 1 - 2²/4(-1)
y (max) = 1 - 4/(-4)
y (max) = 1 - (-1)
y (max) = 1 + 1
y (max) = 2
Learn more about quadratic function on:
https://brainly.com/question/1214333
#SPJ1
Hannah walks up to a water tank that can hold up to 22 gallons of soda. When it is active, a drain empties soda from the tank at a constant rate. When Hannah first sees the tank, it contains 16 gallons of soda. Five minutes later, the tank contains 7 gallons of soda.
How many more minutes BEFORE Hannah arrived was the water tank completely full?
PLEASE ONLY ANSWER IF YOU KNOW THE CORRECT ANSWER. WILL VOTE BRAINLIEST OF ANSWER IS CORRECT. 5 POINTS!
Answers
Minutes it will take the tank to drain completely is 3.88.
What is unit rate?There is independent quantity, and a quantity which depends on it (dependent quantity). When independent quantity moves by a unit measurement (single unit increment), the increment in dependent quantity is called rate of increment of dependent quantity per unit increment in independent quantity
To find the rate =(the time the water takes to leave the tank)/ (the amount of water leaving the tank)
Jada saw 9 gallons of water leave the tank in five minutes. ( The two gallons was obtained from 16-7 = 9)
The rate at which the tank is being emptied is 9 gallons/5 minutes = 1.8 gallons per minute;
For the tank to be empty, it has to lose all 7 gallons of water it has;
1 minute 1.8 gallons are lost
x minutes 7 gallons are lost
By solving;
x = 7/1.8 = 3.88 minutes
Hence, the time taken at the rate will be 3.88 minutes
Learn more about rate on;
brainly.com/question/19493296
#SPJ1
A jet flies 405 miles in 5 hours. At this rate. how far could the jet fly in 15 hours? PLS
Answers
Answer: 1215 miles
Step-by-step explanation:
405 miles in 5 hours is 81 mph so you multiply that mph by the amount of hours you want (15) so 81 x 15 = 1215
the given scatterplot shows the average annual global surface temperature, in degrees celsius, for each year from 2000 to 2015. the line drawn is the least squares line for the data set.
Answers
The scatterplot with the least squares line provides insights into the relationship between average annual global surface temperature and the years from 2000 to 2015, allowing us to assess trends, strength of correlation, and make predictions within certain limitations.
The scatterplot represents the relationship between the average annual global surface temperature, in degrees Celsius, and the corresponding years from 2000 to 2015. The line drawn on the plot is the least squares line, which is the best fit line that minimizes the overall distance between the observed data points and the line.
The least squares line is determined using a statistical method called linear regression. It calculates the equation of a straight line that represents the trend in the data. This line serves as a mathematical model to estimate the average temperature based on the year.
By analyzing the scatterplot and the least squares line, we can make several observations. Firstly, we can see whether the temperature has been increasing, decreasing, or remaining relatively stable over the given years. If the slope of the line is positive, it indicates a positive correlation, implying that the temperature has been increasing. Conversely, a negative slope suggests a decreasing trend.
Additionally, we can evaluate the strength of the relationship between temperature and time by examining how closely the data points cluster around the line. If the points are closely grouped around the line, it suggests a strong correlation, indicating that the line is a good representation of the data. On the other hand, if the points are more scattered, the correlation may be weaker.
Furthermore, the line can be used to predict the average annual global surface temperature for future years beyond the data range of 2000 to 2015. However, it's important to note that such predictions should be made with caution and considering other factors that may affect global temperatures, such as climate change and natural variability.
for such more question on least squares
https://brainly.com/question/3617398
#SPJ8
Question
The given scatterplot shows the average annual global surface temperature, in degrees celsius, for each year from 2000 to 2015. the line drawn is the least squares line for the data set.
6x + 3 = 5x − 8
-11
11
5
-5
Answers
Answer:
x=-5
Step-by-step explanation:
6x+3=5x-8 subtract 5x from both sides
x+3=-8x subtract 3 from both sides
x=-5
Answer:
x = - 11
Step-by-step explanation:
6x + 3 = 5x − 8
Subtract 5x from both sides.
6x + 3 − 5x = −8
Combine 6x and −5x to get x.
x + 3 = −8
Subtract 3 from both sides.
x = −8 − 3
Subtract 3 from −8 to get −11.
x= −11
Is this answer right?

Answers
Answer:
that is the correct answer.
Step-by-step explanation:
Question * Let D be the region enclosed by the two paraboloids z = 3x² + 12/²4 y2 z = 16-x² - Then the projection of D on the xy-plane is: 2 None of these 4 16 This option This option = 1 This opti
Answers
The correct option would be "None of these" since the projection is an ellipse and not any of the given options (2, 4, 16, or "This option").
To determine the projection of the region D onto the xy-plane, we need to find the intersection curve of the two paraboloids.
First, let's set the two equations equal to each other:
3x² + (12/24)y² = 16 - x²
Next, we simplify the equation:
4x² + (12/24)y² = 16
Multiplying both sides by 24 to eliminate the fraction:
96x² + 12y² = 384
Dividing both sides by 12 to simplify further:
8x² + y² = 32
Now, we can see that this equation represents an elliptical shape in the xy-plane. The equation of an ellipse centered at the origin is:
(x²/a²) + (y²/b²) = 1
Comparing this with our equation, we can deduce that a² = 4 and b² = 32. Taking the square root of both sides, we have a = 2 and b = √32 = 4√2.
So, the semi-major axis is 2 and the semi-minor axis is 4√2. The projection of region D onto the xy-plane is an ellipse with a major axis of length 4 and a minor axis of length 8√2.
Learn more about ellipse here :-
https://brainly.com/question/12043717
#SPJ11
SOMEBODY PLEASE HELP

Answers
Please mark brainliest! I’d appreciate it
In 1995, Derek Jeter's batting average was 0.250; in 1996, his batting average was 0.314. David Justice's batting average in 1995 was 0.253 and was 0.321 in 1996. The team statistician claims Jeter's overall average was better than Justice's average. What may make this claim possible
Answers
Simpson's Paradox makes this claim possible.
The phenomenon whereby particular trends are prevalent in small data portions but are not evident or an inverse trend is observed when the portions are joined together is known as Simpson's paradox.
Whereby the data for calculating the batting averages as found online are given as follows:
Season Derek Jeter David Justice
1995 12/48 = 0.250 104/411 ≈ 0.253
1996 183/582 ≈ 0.314 45/140 ≈ 0.321
The overall hits to the overall bat's ratio are:
(183 + 12)/(582 + 48) ≈0.310 (104+45)/(411+140) = 0.27
This shows that Derek Jeter's overall average was better than Justice's average.
Thus, Simpson's Paradox makes this claim possible.
To know more about Simpson's Paradox visit: brainly.com/question/28447378
#SPJ4
As per the given average, the team statistician claims Jeter's overall average was better than Justice's average is 0.27
Here we have given that the following table of data is presented
Time, Score of Derek Jeter Score of David Justice
At 1995, ≈ 0.250 ≈ 0.253
At 1996, ≈ 0.314 ≈ 0.321
Then the overall score for Derek Jeter is calculated by
=> (183 + 12)/(582 + 48) ≈0.310
And the overall score for David Justice is calculated as
=> (104+45)/(411+140) = 0.27
Here the resulting values shows that Derek Jeter's overall average was better than Justice's average
To know more about Average here.
https://brainly.com/question/16956746
#SPJ4
2. Paris has $500 in a savings account at the beginning of the summer. She wants to have at least $200 in the account by the end of the summer. She withdraws $25 each week for food and clothes. a. Write an inequality that represents Paris's situation. b. How many weeks can Paris withdraw money from her account? Justify your answer.
Answers
a) 500 -25x ≥ 200 b) 12 weeks
1) Gathering the data
$500
At least : ≥ 200
Withdrawal = -25
A) Since she wants at least 200 in the account, and the summer has 12 weeks, We can write this inequality:
500 - 25x ≥ 200
B) To find how many weeks we need to solve an equation
500-25x= 200
-25x = 200 -500
-25x = -300
25x = 300
x=12
Under these conditions, 12 weeks in the 13th week she won't be able to keep at least $200 in her account with these weekly withdrawals
Need help asap pls pls pls

Answers
Answer:
bqidhiwodxh
Step-by-step explanation:
627e29302990331 e7894094902
27290[
What is the slope of the line ?

Answers
Step-by-step explanation:
The slope of a line characterizes the direction of a line. To find the slope, you divide the difference of the y-coordinates of 2 points on a line by the difference of the x-coordinates of those same 2 points .
Answer:
To find the slope, you will have to divide the difference of the y-coordinates of 2 points on a line by the difference of the x-coordinates of those h same 2 points .
Step-by-step explanation:
someone help this question is worth 50 points! What ratios are equivalent to the ratio 24:4
A.) 6:1
B.) 12:2
C.) 4:24
D.) 48:8
E.) 18:3
F:) 1:6

Answers
Step-by-step explanation:
just put the ratios into a fraction if x:y then x/y
A.)6/1=6
B.)12/2=6
C.)4/24=1/6
D.)48/8=6
E.)18/3=6
F.)1/6
24/4=6 so A, B, D, and E are equivilant to the ratio 24/4
Hope that helps :)
Answer:
6:1 ,12:2, 48:8
Step-by-step explanation:
24:4
24 ÷ 4 =6 and 4÷4 =1
6:1
24:4
24÷2 =12 , 4÷2=2,
12:2
48:8
24×2=48, 4×2=8
48:8
Given: The two functions below, f(x) and g(x). Find: How do the value of each functions outputs compare when x=0?
f(x)< g(x).
g(x)=f(x)
f(x)> g(x)

Answers
We will see that, when evaluated in x = 0, g(x) is larger than f(x).
How to compare the functions when x = 0?First, we can see that:
g(x) = x + 3
Then, evaluating it in x = 0 we get:
g(0) = 0 + 3 = 3
Now, if we go to the table that represents f(x), we can see that it has the point (0, -6).
Then we can get:
f(0) = -6
With that, we can conclude that: g(0) > f(0), so the correct option is the first one.
If you want to learn more about evaluating functions:
https://brainly.com/question/1719822
#SPJ1