Which option is right and how do i do the work

Answer:

multiply a term by 2 and add 1 to get the next term

Step-by-step explanation:

3×2=6 +1 =7

7×2=14+1= 15

15×2=30+1=31

Answer:

  Multiply a term by 2 and add 1 to get the next term

Step-by-step explanation:

The first differences of terms are ...

  7 -3 = 4

  15 -7 = 8

  31 -15 = 16

We notice that these increase by a factor of 2. This signifies an exponential sequence. That factor (2) will be the value that each term is multiplied by to get the next. This eliminates the choices "add 4" and "multiply a term by 3 ...".

Trying the remaining two choices, we find that the one that fits is the one shown above.

  3+7 ≠ 15, so "the sum of the two preceding terms" doesn't work

  2(3) +1 = 7; 2(7) +1 = 15; 2(15) +1 = 31, so "multiply by 2 and add 1" works fine

The average rate of change of the function f(x) on the interval -9 ≤ x ≤ 0 is:

R = -2

For any function f(x), we define the average rate of change on an interval [x₁, x₂] (such that the interval belongs to the domain of the function) as:

R = [ f(x₂) - f(x₁)]/(x₂ - x₁)

In this problem the function is:

f(x) = x^2 + 7x + 9

And the interval is [-9, 0]

Then the average rate of change will be:

R = [ f(0) - f(-9)]/(0 - (-9))

R = [ 0^2 + 7*0 + 9 - (-9)^2 - 7*(-9) - 9]/9

R = [-18]/9 = -2

The average rate of change of f(x) is -2.

Learn more about rates of change:

https://brainly.com/question/8728504

#SPJ1

21 child tickets were sold that day.

Let x be the number of child tickets sold and y be the number of adult tickets sold.

The total revenue generated from the child tickets is 5.9x dollars and the total revenue generated from the adult tickets is 9y dollars,

so the total revenue generated is 5.9x + 9y dollars.

The number of adult tickets sold is four times the number of child tickets sold,

so y = 4x.

Substituting this into the previous equation gives

5.9x + 9(4x) = 879.9.

Simplifying the equation,

5.9x + 36x = 879.9,

so 41.9x = 879.9.

Solving for x,

we get x = 21.

Therefore, 21 child tickets were sold that day.

To know more about equation visit:

https://brainly.com/question/14578396

#SPJ11

Deon's Coffee Shop used 26 pounds of type A coffee.

Let's consider Deon's Coffee Shop, which used "a" pounds of type A coffee and "4a" pounds of type B coffee. The total cost of the blend is $578.50, so we can equate the total cost of the type A and type B coffee to that amount. This leads us to the following equation: 5.45a + 4.20(4a) = 578.50.

To solve the equation, we simplify it: 5.45a + 16.80a = 578.50. Combining like terms, we get 22.25a = 578.50.

To find the value of "a," we divide both sides of the equation by 22.25. Therefore, a = 26. Hence, Deon's Coffee Shop used 26 pounds of type A coffee.

Learn more about coffee

https://brainly.com/question/29758432

#SPJ11

Answer: 440-25h = m

Step-by-step explanation:

She makes 25 dollars per hour (25h=m)

If u subtract the amount that the console costs the equation becomes

440-25=m

Im assuming u are in 7th grade math which is what i was in last year so i hope this helps! :)

The standardized value of X = 16, given that X is a normal random variable with mean = 20 and standard deviation = 2, is -2.

To find the standardized value of X = 16, we need to convert it into a standard normal random variable by using the formula for standardization.

The standardization process involves subtracting the mean of the random variable and dividing by its standard deviation.

Given that X has a mean of 20 and a standard deviation of 2, the formula for standardization is:

Z = (X - μ) / σ

Where Z represents the standardized value, X is the original random variable, μ is the mean, and σ is the standard deviation.

Plugging in the values, we have:

Z = (16 - 20) / 2

Z = -4 / 2

Z = -2

Therefore, the standardized value of X = 16 is -2.

Learn more about standard deviation

brainly.com/question/13498201

#SPJ11

On calculating the rate of change, it can be obtained that

Date on which the flower was 16.5 cm tall = 13 April

What is rate of change?

Suppose there are two quantities. On changing the value of one quantity, the rate at which the other quantity changes is called rate of change.

Here,

On April 8th, a flower at blooming acres florist was 15. 0 centimeters tall.  On April 16th, the flower was 17. 4 centimeters tall.

Rate of change =

                            \(\frac{17.4 - 15}{16 - 8}\\\frac{2.4}{8}\\\)

                            0.3 cm/day

Difference between 16.5 cm and 15 cm = 16.5 - 15  = 1.5 cm

Number of days required to grow from 15 cm to 16.5 cm = \(\frac{1.5}{0.3} =5\) days

Date on which the flower was 16.5 cm tall = 8th April + 5 = 13 April

To learn more about rate of change, refer to the link-

https://brainly.com/question/11859175

#SPJ4

The length of the third of the triangle is 7.76 cm

It is given that the length of the two sides is 6.5 cm and 9.4 cm.

And the angle between them is 131 degrees.

Let a = 6.5 cm

b = 9.4 cm and ∠C = 131 °

According to the law of cosines, we have

\(c^{2} = a^{2} +b^{2} -2abcosC\\\\\)

Putting all the given parameters in the given equation, we have

\(c^{2} = (6.5)^{2} +(9.4)^{2} -2*6.5*9.4cos131\\\\c^{2} = 42.25 + 90.25 - 72.1497\\\\c^{2} = 60.3503\\\\c = \sqrt{60.3503} \\\\c = 7.76 cm\)

Thus, the length of the third of the triangle is 7.76 cm

To read more about triangles, visit https://brainly.com/question/2773823

#SPJ4

As per the given measurement, you would need to burn an extra 500 calories every day in order to lose 9 pounds in 63 days, assuming that the rest of your diet remains constant.

We know that in order to lose 1 pound of body weight, you need to burn an extra 3500 calories. Therefore, to lose 9 pounds, you would need to burn an extra 31,500 calories

=> (9 pounds x 3500 calories per pound).

If you divide this number by the number of days in which you want to achieve this goal, you'll find the amount of calories you need to burn each day. In this case, it would be:

31,500 calories / 63 days = 500 calories per day

To know more about measurement here

https://brainly.com/question/2107310

#SPJ4

Option D: Tim's with a y-intercept of $2,780.

Given that:

Equation given by Paul:

\(y - 1400 = 56(x + 26)\\or\\y = 56x + 2856\)

Data given by Tim:

Total amount at the end of 8 months = $4,500

Interest per month = $225

Thus principal amount can be calculated by: \(4580 - 8 \times 225 = 2780\) in dollars.

Thus the equation for Tim will be:

\(y = 2780 + 225x\)

Thus it is visible that the y-s intercept for Tim's equation is smaller ( since 2780 < 2856).

Thus Option D is correct.

Learn more here:

https://brainly.com/question/25857212

The critical value that should be used in constructing the confidence interval is (0.150 , 0.166).

The given parameter is as follows,

t\alpha /2,df = 2.473

Margin of error = E = t\alpha/2,df * (s sqrt n)

= 2.473 * (0.0171 / \sqrt28)

Margin of error = E = 0.008

If the populace preferred deviation (σ) is known, a speculation take a look at carried out for one populace imply is known as one-imply z-take a look at or definitely z-take a look at. A z-take a look at is a speculation take a look at for trying out a populace imply, μ, in opposition to a intended populace imply, μ0.

The 98% confidence interval estimate of the population mean is,

\bar x - E < \mu < \bar x + E

0.158 - 0.008 < \mu < 0.158 + 0.008

0.150 < \mu < 0.166

(0.150 , 0.166)

To learn more about deviation check the link below:

https://brainly.com/question/475676

#SPJ4

The height of the 10th bounce of the ball will be 0.6 feet.

A geometric sequence is a sequence in which each term is found by multiplying the preceding term by the same value.

The nth term of the geometric sequence is given by

\(\sf T_n=ar^{n-1}\)

Where,

According to the given question.

During the first bounce, height of the ball from the ground, a = 4.5 feet

And, the each successive bounce is 73% of the previous bounce's height.

So,

During the second bounce, the height of ball from the ground

\(\sf = 73\% \ of \ 10\)

\(=\dfrac{73}{100}(10)\)

\(\sf = 0.73 \times 10\)

\(\sf = 7.3 \ feet\)

During the third bounce, the height of ball from the ground

\(\sf = 73\% \ of \ 7.3\)

\(=\dfrac{73}{100}(7.3)\)

\(\sf = 5.33 \ feet\)

Like this we will obtain a geometric sequence 7.3, 5.33, 3.11, 2.23,...

And the common ratio of the geometric sequence is 0.73

Therefore,

The sixth term of the geometric sequence is given by

\(\sf T_{10}=10(0.73)^{10-1\)

\(\sf T_{10}=10(0.73)^{9\)

\(\sf T_{10}=10(0.059)\)

\(\sf T_{10}=0.59\thickapprox0.6 \ feet\)

Hence, the height of the 10th bounce of the ball will be 0.6 feet.

Find out more information about geometric sequence here:

brainly.com/question/11266123

Answer:

1) The equation for the of the ball in y = a·(x - h)² + k is;

y = -16·(x - 5)² + 25

2) The height of the dock, d =  -375 feet below the water level

Step-by-step explanation:

1) The question is with regards to quadratic function representing projectile motion

The given parameters are;

The height the ball reaches 4 seconds after Sarah kicked the ball = 9 feet

The time the ball hits the water = 6 seconds after reaching the 9 feet height

The form of the quadratic equation representing the motion is given as follows;

y = a·(x - h)² + k = a·x² - 2·a·h·x + a·h² + k

Let 'x' represent the time of motion of the ball, and let 'a', represent the acceleration due to gravity, we have;

The equation for the ball, y = a·(x - h)² + k

Where;

(h, k) = The coordinates of the vertex

h = The horizontal component of the vertex coordinate = 0

Therefore, we have;

When x = 0, y = d

d = -16·(0 - h)² + k =  -16·h² + k

d = -16·h² + k  

When x = 4, y = 9 - d

9 - d = -16(4 - h)² + k = -16(4 - h)² + k

When x = 2, y = d

d = -16(2 - h)² + k

When x = 6, y = 9

9 = -16(6 - 5)² + k

When x = 8, y = d

d = -16(8 - h)² + k

-16(8 - h)² - (-16(2 - h)²) = 0

h = 5

From 9 - d = -16(4 - h)² + k = -16(4 - 4)² + k

d = 9 - k

9 = -16(6 - h)² + k

k = 9 + 16(6 - 5)² = 25

d = 9 - k = 9 - 25 = -16

Therefore, h = 5, k = 25

The equation for the of the ball in y = a·(x - h)² + k is therefore;

y = -16·(x - 5)² + 25

2) When x = 0, y = d, ∴ d = -16(0 - 5)² + 25 = -375 feet below the water

The height of the dock, d =  -375 feet below the water level

The sample standard deviation is approximately 0.83.

Sample size \(($n$)\) = 36

Population mean \(($\mu$)\) = 50

Population standard deviation \(($\sigma$)\) = 5

The sample standard deviation, denoted as \($s$\) can be estimated using the formula:

\(\[ s = \sqrt{\frac{\sum_{i=1}^{n}(x_i - \bar{x})^2}{n-1}} \]\)

where:

\($x_i$\) represents the individual data points in the sample

\($\bar{x}$\) is the sample mean

In this case, since we don't have individual data points, we can use the population standard deviation as an estimate for the sample standard deviation when the sample size is relatively large (as in this case \($n = 36$\)). This approximation is known as the standard error of the mean.

Therefore, the sample standard deviation can be approximated as:

\(\[ s \approx \frac{\sigma}{\sqrt{n}} \]\)

Substituting the given values:

\(\[ s \approx \frac{5}{\sqrt{36}} = \frac{5}{6} \] = 0.83\)

Hence, the sample standard deviation is approximately 0.83.

Learn more about sample standard deviation: https://brainly.com/question/18567452
#SPJ11

Answer:

31/6

Step-by-step explanation:

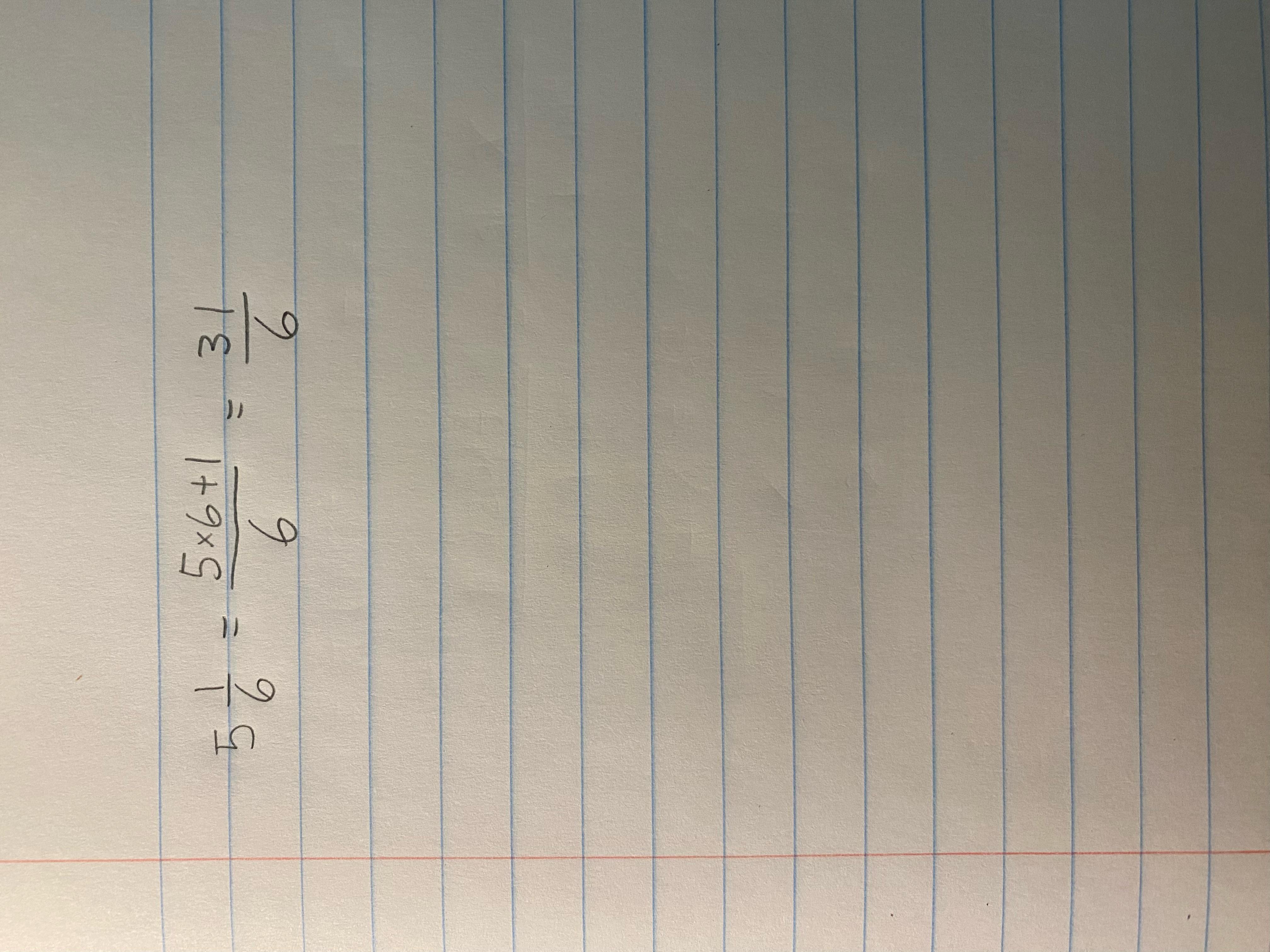
Answer:

31/6

Step-by-step explanation:

5 1/6

5×6=30

30+1=31

31/6=improper fraction

Answer:

90°

Step-by-step explanation:

Given the vectors:

\(\displaystyle{\vec v = \langle -6, -3\rangle \ \: \text{and} \ \: \vec u = \langle 4, -8 \rangle}\)

You can find the angle between two vectors by solving for θ in the equation:

\(\displaystyle{\vec v \times \vec u = |\vec v | |\vec u| \cos \theta}\)

Where:

\(\displaystyle{\vec v \times \vec u = v_xu_x + v_yu_y}\\\\\displaystyle{|\vec v| = \sqrt{v_x^2 + v_y^2}}\\\\\displaystyle{|\vec u| = \sqrt{u_x^2+u_y^2}}\)

Therefore:

\(\displaystyle{\vec v \times \vec u = |\vec v | |\vec u| \cos \theta}\\\\\displaystyle{(-6)(4)+(-3)(-8) = \sqrt{(-6)^2+(-3)^2} \cdot \sqrt{4^2+(-8)^2} \cos \theta}\\\\\displaystyle{-24+24=\sqrt{36+9}\cdot \sqrt{16+64}\cos \theta}\\\\\displaystyle{0=\sqrt{45}\cdot \sqrt{80}\cos \theta}\\\\\displaystyle{\dfrac{0}{\sqrt{45}\cdot \sqrt{80}}=\cos \theta}\\\\\displaystyle{0=\cos \theta}\\\\\displaystyle{\theta = 90^{\circ}}\)

Therefore, the angle between two vectors is 90 degrees.

The system of equations has no solution because both equations are inconsistent. In other terms, the equation system is said to be inconsistent.

A mathematical theorem is a technique that connects two statements and utilizes the equivalent symbol (=) to signify equality. In algebra, an equation describes a mathematical statement that shows the equivalence of two formulas. For example, in the computation 3x + 5 = 14, the equal sign inserts a space between the values 3x + 5 and 14. A mathematical formula can be used to explain the connection that exists between the sentences written across each side of a letter. The logo and the programming are sometimes the same. For example, 2x - 4 equals 2.

In the first equation, the left side has 3+2+3 while the right side has 7(-1)-4. We get 8 by simplifying the left side. We get -11 by simplifying the right side. Thus far, we have:

8 = -11

Because this is not true, the first equation is incoherent.

In the second equation, the left side has 3+5 while the right side has 7(-1)-4. We get 8 by simplifying the left side. We get -11 by simplifying the right side. Thus far, we have:

8 = -11

This is likewise false, so the second equation is similarly flawed.

The system of equations has no solution because both equations are inconsistent. In other terms, the equation system is said to be inconsistent.

To know more about equation visit:

https://brainly.com/question/649785

#SPJ1

the required parent function is f(x) = x² which supports the data in the table. Option A is correct.

Functions are the relationship between sets of values. e g y=f(x), for every value of x there is its exists in a set of y. x is the independent variable while Y is the dependent variable.

Here,
We are given a table from which we have to determine which parent function among the option supports that data in the table.

So,

A.
f(x) = x²

Substitute each value from the table in the above expression,
f(-2) = 4
f(-1) = 1

f(0) = 0
f(1) = 1

f(2) = 4

Now,
B.
f(x) = {x|

Substitute each value from the table in the above expression,

f(-2) = 2   [it does not match with the given data]

Thus, the required parent function is f(x) = x². Option A is correct.

Learn more about function here:

brainly.com/question/21145944

#SPJ1

Answer: 8575/2

Step-by-step explanation:

Answer:

: w ≤ - 6

Step-by-step explanation:

Macy had 3 appointments.

Logan had 5 appointments.

What is the quadratic equation?

A quadratic equation is a type of polynomial equation of degree 2, which is written in the form of "ax^2 + bx + c = 0", where x is the variable and a, b, and c are constants. The solutions to a quadratic equation can be found using the quadratic formula: x = (-b ± √(b^2 - 4ac))/2a.

Part A:

Let x be the number of appointments Macy had.

We know that the total income (60x + 40) must equal 220.

Therefore, the equation representing the situation is:

60x + 40 = 220

To solve for x, we can subtract 40 from both sides:

60x = 180

Finally, we divide both sides by 60 to get:

x = 3

Macy had 3 appointments.

Part B:

Let y be the number of appointments Logan had.

We know that the total profit (70y + 50 - 20y) must equal 300.

Therefore, the equation representing the situation is:

50y + 50 = 300

To solve for y, we can subtract 50 from both sides:

50y = 250

Finally, we divide both sides by 50 to get:

y = 5

Logan had 5 appointments.

To learn more about quadratic equations, Visit

https://brainly.com/question/1214333

#SPJ1

Answer:

2-10n=.............what. We can't figure out n given 2-10n without a solution

Step-by-step explanation:

Step-by-step explanation:

the slope intercept form is

y = ax + b

the slope (a) is always the factor of x in such a normalized form. and we know a = 1.

since we have the slope and a point we can start with the point-slope form

y - y1 = a(x - x1)

where (x1, y1) is a point on the line

and then transform :

y - -6 = 1×(x - -9)

y + 6 = x + 9

y = x + 3

Answer:

\(y=x+3\)

Step-by-step explanation:

Answer:

$325

Step-by-step explanation:

t +b = 582

t = b - 68

b - 68 + b = 582

2b = 582 + 68

2b = 650

2/2 b = 650 / 2

b = 325

Answer:

y=11

Step-by-step explanation:

Hi there!

We want to find the equation of the line that passes through the point (-8, 11) and is perpendicular to x=-15

If a line is perpendicular to another line, it means that the slopes of those lines are negative and reciprocal; in other words, the product of the slopes is equal to -1

The line x=-15 has an undefined slope, which we can represent as 1/0, which is also undefined.

To find the slope of the line perpendicular to x=-15, we can use this equation (m is the slope):

\(m_1*m_2=-1\)

\(m_1\) in this instance would be 1/0, so we can substitute it into the equation:

\(\frac{1}{0} *m_2=-1\)

Multiply both sides by 0

\(m_2=0\)

So the slope of the new line is 0

We can substitute it into the equation y=mx+b, where m is the slope and b is the y intercept:

y=0x+b

Now we need to find b:

Since the equation passes through the point (-8,11), we can use its values to solve for b.

Substitute -8 as x and 11 as y:

11=0(-8)+b

Multiply

11=0+b, or 11=b

So substitute into the equation:

y=0x+11

We can also write the equation as y=11

Hope this helps!

Answer:

its is a

Step-by-step explanatioits n:

The equation of the line will be y = (1/3)x + ( 11 / 3 ). The correct option is B.

It is defined as the relation between two variables, if we plot the graph of the linear equation we will get a straight line.

Let m be the slope of the line and c is the y-intercept of the line.

The equation of the line is given as,

y = mx + c

The product of the slopes of the perpendicular lines is equal to -1.

y = 3x – 2

m = 3

Then the slope of the perpendicular line will be -1 / 3. The equation of the line will be written as below:-

y = (-1 / 3)x + c

The line is passing through the point  (–2, 3). Then calculate the value of the constant.

3 = (-1 / 3 )2 + c

c = 11 / 3

The equation of the line will be:-

y = (-1/3)x + (11/ 3)

Therefore,  the equation of the line will be y = (1/3)x + ( 11 / 3 ). The correct option is B.

To know more about the equation of the line follow

https://brainly.com/question/18831322

#SPJ2

Answer:

Well..They gave you the hint all you have to do is apply the formula

hint: the way a quadratic formula is written is \(ax^2 + bx + c\)

So lets do this

axis of symmetry = \(\frac{-b}{2a} = \frac{-(-12)}{2(-3)} = \frac{12}{-6} = -2 = x\)

Hope that answers your question

Don't hesitate to comment if you are confused about something

Step-by-step explanation:

To determine which of the following graphs does not represent a function.

Explanation:

It is given that,

Using vertical line test, the above graph becomes,

Here,

The vertical line cuts the curve at more than one points.

Hence, option A) is not a function.

Answer:

y=-3x-12

Step-by-step explanation:

:)

The words that fills the blank space on the method used to find the length of the diagonal AG, using Pythagorean Theorem are as follows;

Blank 1; The Pythagorean Theorem

Blank 2; Square root of 73

Blank 3; A leg

Blank 4; The hypotenuse

Blank 5; 9.4 cm

Pythagoras Theorem indicates that the square of the longest side of a right triangle is equivalent to the sum of the square of the other two sides.

The diagonals from point A to point G in the cuboid can be found using Pythagoras Theorem as follows;

The diagonal of the base rectangle, ABCD, is found as follows;

AC = √(8² + 3²) = √(73)

Using the side CG as the leg of the right triangle ΔACG, with AG being the hypotenuse, we get;

CG = 4 indicated in the diagram in the question

(AG)² = (AC)² + (CG)²

(AG)² = 73 + 4² = 89

AG = √(89) ≈ 9.4

The completed statement is therefore;

Learn more about Pythagorean Theorem here:

https://brainly.com/question/15252776

#SPJ1