Which of these is the standard form of the following function?
f(x) = -9(x + 5)2 + 4
f(x) = 9x2 − 90x − 221
f(x) = -9x2 − 90x − 221
f(x) = 9x2 − 180x + 221
f(x) = -9x2 − 180x − 221
Answers
Answer:
We conclude that the standard form of the given function is:
\(f(x)=-9x^2-90x-221\)
Hence, option B is correct.
Step-by-step explanation:
We know that the standard form of the quadratic function is of the form
\(f\left(x\right)\:=\:ax^2\:+\:bx\:+\:c\)
Given the function
\(f(x)=-9\left(x\:+\:5\right)^2\:+\:4\)
as (x+5)² = x² + 10x + 25
\(f(x)=-9\left(x^2+10x+25\right)+4\)
Expanding -9(x² + 10x + 25) = -9x² - 90x - 225
\(f\left(x\right)\:=-9x^2-90x-225+4\)
simplifying
\(f(x)=-9x^2-90x-221\)
Therefore, we conclude that the standard form of the given function is:
\(f(x)=-9x^2-90x-221\)
Hence, option B is correct.
Answer:
Hope this helps!
Step-by-step explanation:

Related Questions
plz i need help i don't understand it

Answers
Answer:
y=5,2 and -3
we have to put the values of X and then solve the equation.
Have a good dayX=-3 the y is -1
x=0 the y is 2
x=5 the y is -3
Hope this helps ;)
Certain pieces of antique furniture increased very rapidly in price in the 1970s and 1980s. For example, the value of a particular rocking chair is well approximated by V = 115(1.6), where V is in dollars andtis the number of years since 1975. Find the rate, in dollars per year, at which the price is increasing.
rate = dollars/yr
Answers
The given equation for the value of the rocking chair is V = 115(1.6)^t, where t is the number of years since 1975. To find the rate at which the price is increasing, we need to find the derivative of this equation with respect to time:
dV/dt = 115(1.6)^t * ln(1.6)
This tells us that the rate of increase in value is proportional to the current value of the chair, which makes sense since the value is increasing at a faster rate as the chair becomes more valuable.
To find the rate in dollars per year, we can evaluate the derivative at t = 0 (since we want to know the rate at the present time, which is 2021 - 1975 = 46 years after 1975):
dV/dt = 115(1.6)^0 * ln(1.6) = 30.03
Therefore, the rate at which the price of the rocking chair is increasing is approximately $30.03 per year.
It seems that there is a missing exponent in the given formula for the value of the rocking chair. The correct formula should include an exponent 't' as in V = 115(1.6)^t, where V is the value in dollars and t is the number of years since 1975.
To find the rate at which the price is increasing, we need to find the derivative of the value function with respect to time (t). The derivative of V = 115(1.6)^t is dV/dt = 115 * ln(1.6) * (1.6)^t.
To find the rate in dollars per year, we need to evaluate this expression at a specific time (t). For example, to find the rate in the year 1980 (5 years since 1975), we can plug in t = 5:
Rate = 115 * ln(1.6) * (1.6)⁵ ≈ $419.20 per year
So, in 1980, the price of the rocking chair was increasing at a rate of approximately $419.20 per year.
Visit here to learn more about derivative brainly.com/question/30365299
#SPJ11
What is the measure if Angle JKL?
Answers
The measure of the angle JKL as per the attached diagram is equal to 97 degrees.
As per in the question,
Diagram is attached.
Angle JKL is linear pair angle with given angle of measure 83 degrees.
Sum of the pair of linear pair is always equal to 180 degrees.
Let 'x' be the measure of angle JKL, we get,
83° + m ∠JKL = 180°
Subtract 83° from both the side of the equation we get,
⇒ 83° - 83° + m ∠JKL = 180° - 83°
⇒ m ∠JKL = 97°
Therefore, the measure of the angle JKL as per the attached diagram is equal to 97 degrees.
Learn more about angle here
brainly.com/question/28451077
#SPJ4

Linda needs to buy some pencils. Brand A has a pack of 48 pencils for $7. 97. Brand B has a pack of 72 pencils for $9. 88. Find the unit price for each brand. Then state which brand is the better buy based on the unit price. Round your answers to the nearest cent
Answers
Answer:
Brand B is the better price because it is approx $0.13 per pencil, and Brand A is more expensive because it is $0.17 per pencil.
Step-by-step explanation:
Brand A:
7.97/48 = 0.16604166666 = approx $0.17 per pencil
Branch B:
9/72 = 0.125 = approx $0.13 per pencil
Brand B is the better price because it is approx $0.13 per pencil and Brand A is more expensive because it is $0.17 per pencil.

Put
–
44,
–
95, and
–
27 in order from least to greatest
Answers
Answer:
27,44,95
Step-by-step explanation:
These numbers are in order from least to greatest, hope this helped!
Answer:
27, 44, 95
Step-by-step explanation:
Since 27 is smaller than 44 and 95 it goes first and since 95 is bigger than 27 and 44 it goes at the end and 44 is in the middle
Two sides of a triangle have lengths 15 and 20. The length of the third side can be any number greater than A and less than
Answers
The third side of the triangle will be less than 35.
What is a triangle?A polygon with three angles, sides and angles is called a triangle.
Given that, Two sides of a triangle have lengths 15 and 20. The length of the third side can be any number greater than A and less than
We know that, triangle inequality theorem states that the sum of any two sides of a triangle is greater than or equal to the third side.
Therefore, length of the third side < 15+20 < 35
Hence, the third side of the triangle will be less than 35.
Learn more about triangles, click;
https://brainly.com/question/2773823
#SPJ1
HELP PLEASE ASAP (no links scammers) WILL GIVE BRAINLEAST

Answers
Answer:
I don't see a question. If you're asking what ratio each final option would be, it would be D.
I need help on these questions

Answers
Answer:
1. 21 hours
2. 21 hours
Step-by-step explanation:
1. If we add up all the time it takes them to build one dog house, we get 210 minutes or 3.5 hours. All we have to do is multiply this by 6 because they are building 6 of these exact dog houses. We would then get the answer 21 hours.
2. For this one, it would take Reece double the time it would take both friends. We know if they are both working it takes 3.5 hours so if it is just one of them working it would take 7 hours. So if she builds 3 it will take 21 hours.
What is not an example of a linear function?
Answers
A quadratic function is not an example of a linear function because it does not satisfy the criteria of being a straight line when graphed.
A quadratic function is not an example of a linear function.
In mathematics, a linear function is a function that can be represented by a straight line when graphed. It has the form f(x) = mx + b, where m is the slope of the line and b is the y-intercept. The graph of a linear function is always a straight line.
On the other hand, a quadratic function is a polynomial function of degree 2. It has the general form f(x) = ax² + bx + c, where a, b, and c are constants and a ≠ 0. The graph of a quadratic function is a curve called a parabola, not a straight line. The shape of the parabola depends on the values of the coefficients a, b, and c.
Therefore, a quadratic function is not an example of a linear function because it does not satisfy the criteria of being a straight line when graphed.
A linear function is a mathematical function that can be represented by a straight line when graphed. It has the general form:
f(x) = mx + b
To know more about quadratic function click here :
https://brainly.com/question/29775037
#SPJ4
will award 100 points

Answers
Answer:
4 and 6 are alternate interior angles.
3 and 7 are corresponding angles.
8 and 1 are same side exterior angles
Answer:
4 or 6 what the other person said was right
Step-by-step explanation:
Three students calculated the volume of a cylinder. Each used a different strategy.
Jada said, "I used the formula V = Bh."
• Andre said, "I found the area of a circular cross section and multiplied it by the
cylinder's height."
Han said, "1 used the formula V = xrh.
For each student, decide if you agree with their strategy. Explain your reasoning.
Answers
I only agree with the first student strategy of multiplying the area of the base with the height.
Volume of a cylinderA cylinder is made up of two circles at the top and the base.
The volume of the cylinder can be expressed as:
V = Bh
where
B is the base area
h is the height of the cylinder
V = πr²h
HEnce I only agree with the first student strategy of multiplying the area of the base with the height.
Learn more on volume of cylinder here; https://brainly.com/question/9554871
Help plz i give brainliest
Answers
Answer:
yo
Step-by-step explanation:
What are the first 10 digits after the decimal point when the fraction $\frac17$ is written in base 16?
Answers
Answer:
The amswer is "2,4,9....."
Step-by-step explanation:
\(x=\frac{1}{7}\\\\x_d=0.\overline{142857}\\\\x_h=0.\overline{249}\\\\\)
by leave you to work out the other 7 digits:
\(\to \frac{1}{7}\approx \frac{a}{16}\\\\a= \text{first hex digit}\\\\a=floor(\frac{16}{7})=2\\\\\)
\(\to \frac{1}{7}- \frac{a}{16}\approx \frac{b}{16^2}\\\\b= \text{second hex digit}\\\\b=floor(\frac{16^2}{7} -16a)=4\\\\\)
\(\to \frac{1}{7}- \frac{a}{16}-\frac{b}{16^2} \approx \frac{c}{16^3}\\\\c= \text{third hex digit}\\\\c=floor(\frac{16^3}{7} -16^2a-16b)=9\\\\\)
Using the omission strategy, what value would be placed in the missing observation in x1?
x1x2
76
22
82
91
32
41
88
Options:
84
No value because excluded
83
90
Answers
The values in the missing observation are:
X1 X2
76 22
82 25
91 32
101 41
88 28
What is an expression?An expression contains terms with addition, subtraction, multiplication, and division.
Example: 2 + 3x + 4y = 7 is an expression.
We have,
x1 x2
76 22
82 __
91 32
__ 41
88 28
The difference between each row are:
76 - 22 = 54
82 - 25 = 57
91 - 32 = 59
101 - 41 = 60
88 - 28 = 60
We see that,
57 - 54 = 3
59 - 57 = 2
60 - 59 = 1
60 - 60 = 0
So,
The difference between the numbers is consecutive as 3, 2, 1, 0.
Thus,
The missing values of X1 and X2 are 101 and 25.
Learn more about expressions here:
https://brainly.com/question/3118662
#SPJ1
Solve for h.
0.8h − 11.49 = 5.67 + 12.9 − 15.9h
Answers
So the right answer is 1.8
Look at the attached picture
Hope it will help you
Good luck on your assignment

Which graph shows y < x2 + 1?
c.
Answers
Answer:
3rd one
Step-by-step explanation:
Answer:C
Step-by-step explanation:took test
Pleas help me see image below (math)
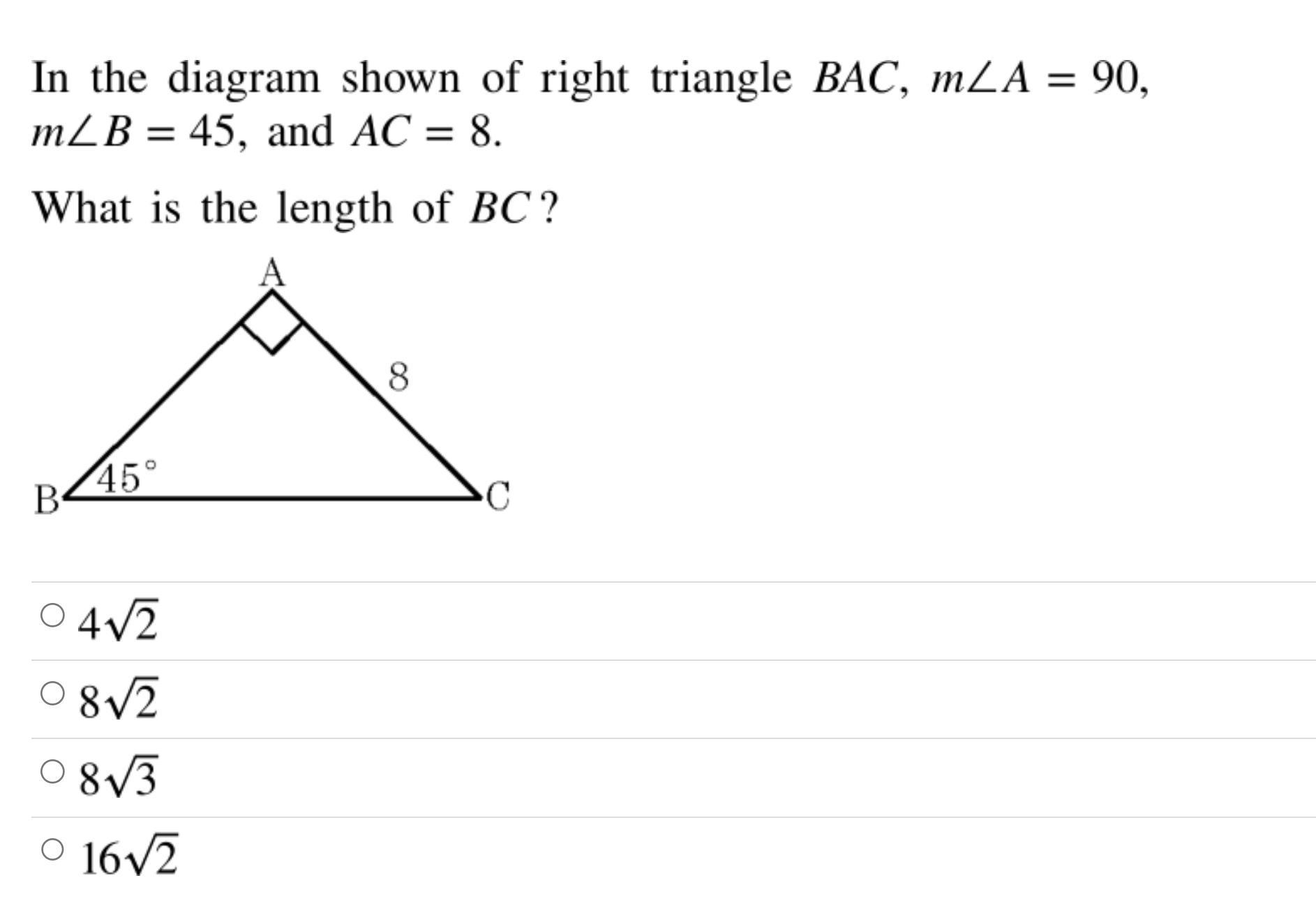
Answers
Answer:
8√2
Step-by-step explanation:
Notice that this is a 45-45-90 triangle (isosceles right triangle). This type of triangle has a property where the ratio between side lengths is x : x : x√2, where x√2 is the measure of the two equal legs and is the measure of the hypotenuse.
Since we know the measure of one of the smaller legs is 8, then we can set x in the ratio to 8 --> 8 : 8 : 8√2
Thus, the length of BC (hypotenuse) is 8√2
ope has $900 in her checking account. she has $ 76 per month that she must pay bills .at most how many months,m, can she pay all of her bills without making any additional deposits?
Answers
Answer:
11 months
Step-by-step explanation:
Answer:11 Months
Step-by-step explanation:
Nine hundred divided 76 equals Months 900÷76=M
Use linear approximation, i.e. the tangent line, to approximate 78.08 as follows. Let f(x) = Ve and find the equation of the tangent line to f(x) at x = 8 in the form y = mx +b. Note: The values of m
Answers
The slope, m, of the tangent line is 1/2.
The equation of the tangent line is y = (1/2)x + (3\(\sqrt{8 - 4}\)).
The approximation of \(3\sqrt{8.05}\) using the tangent line is approximately 4.75705 (rounded to 5 decimal places).
To find the equation of the tangent line to the function \(f(x) = 3\sqrt{x}\) at x = 8, we need to determine the slope, m, and the y-intercept, b, of the tangent line.
The slope of the tangent line can be found by taking the derivative of f(x) with respect to x and evaluating it at x = 8. Let's calculate it:
f(x) = 3\(\sqrt{x}\)
To find the derivative, we can rewrite f(x) as:
f(x) = \(3x^{(1/3)\)
Now, we can differentiate f(x) with respect to x:
f'(x) = (1/3) * 3 * \(x^{(-2/3)\)
=\(x^{(-2/3)\)
Evaluating f'(x) at x = 8:
f'(8) = \(8^{(-2/3)\)
= \(1/8^{(2/3)\)
= 1/2
So, the slope, m, of the tangent line is 1/2.
To find the y-intercept, b, we substitute the point (8, f(8)) = (8, 3\(\sqrt{8}\)) into the equation of the tangent line, y = mx + b, and solve for b:
3\(\sqrt{8}\) = (1/2)(8) + b
= 4 + b
b = 3\(\sqrt{8-4}\)
Therefore, the equation of the tangent line is y = (1/2)x + (3√8 - 4).
Now, we can use this tangent line approximation to approximate 3√8.05. Substituting x = 8.05 into the equation of the tangent line:
3\(\sqrt{8.05}\) ≈ (1/2)(8.05) + (3\(\sqrt{8-4}\))
≈ 4.025 + (3\(\sqrt{8-4}\))
To obtain a decimal approximation, we need to evaluate (3\(\sqrt{8-4}\)) to high precision,we find:
3\(\sqrt{8}\) ≈ 4.73205
Substituting this value back into the approximation:
3\(\sqrt{8.05}\)≈ 4.025 + 4.73205 - 4
≈ 4.75705
Therefore, the approximation of 3\(\sqrt{8.05}\)using the tangent line is approximately 4.75705 (rounded to 5 decimal places).
Learn more about Tangent Line at
brainly.com/question/23416900
#SPJ4
Complete Questions:
Use linear approximation, i.e. the tangent line, to approximate 3\(\sqrt{8.0}\) as follows. Let f(x)=3\(\sqrt{x}\) and find the equation of the tangent line to f(x) at x=8 in the form y=mx+b.
Note: The values of m and b are rational numbers which can be computed by hand. You need to enter expressions which give m and b exactly. You may not have a decimal point in the answers to either of these parts.
m =
b =
Using these values, find the approximation.
3\(\sqrt{8.05}\)≈
Note: You can enter decimals for the last part, but it will has to be entered to very high precision (correct for 6 places past the decimal point).
Add or subtract.
a.
5 + 12 =
14
Answers
Answer:
17
Step-by-step explanation:
12+5=17
I’m somewhat confused by what you are asking if this is not correct.
Find the value of x.

Answers
2x-10= 180
2x= 190
x= 95
hope this helps!
Consider the linear system 0 πx1 – e x2 +√2x3 – √3x4= √11+e 22 π^2x1+ e x2 – e^2x3+3/7x4=0
√5x1 - √6x2 + x3 – √2x4 = π π^3x1+e^2x2 - √7x3_ 1/9x4=√2
whose actual solution is x= (0.788, – 3.12, 0.167, 4.55)^T. Carry out the following computations using 4 decimal places with rounding: (1.1) Write the system as a matrix equation. (2) (1.2) Solve the system using: (a) Gaussian elimination without pivoting. (7) (b) Gaussian elimination with scaled partial pivoting. (c) Basic LU decomposition
Answers
(1.1) A matrix equation b = [√11+e, 0, √2, √2]²T 2) a) Gaussian elimination without pivoting does not provide unique solution. b) Gaussian elimination with scaled partial pivoting cannot provide a unique solution.(c) Basic LU decomposition is x = [0.788, -3.12, 0.167, 4.55]²T.
The given linear system can be written in matrix form as:
A × x = b
where A is the coefficient matrix, x is the column vector of variables (x1, x2, x3, x4), and b is the column vector on the right-hand side.
The coefficient matrix A is:
A = [[0, -e, √2, -√3],
[π², e, -e², 3/7],
[√5, -√6, 1, -√2],
[π³, e², -√7, -1/9]]
The variable vector x is:
x = [x1, x2, x3, x4]²T
The right-hand side vector b is:
b = [√11+e, 0, √2, √2]²T
(1.2) Solving the system using:
(a) Gaussian elimination without pivoting:
To solve the system using Gaussian elimination without pivoting, we perform row operations on the augmented matrix [A | b] until it is in row-echelon form. Then back-substitute to find the values of x.
The augmented matrix [A | b] is:
[0, -e, √2, -√3 | √11+e]
[π², e, -e², 3/7 | 0]
[√5, -√6, 1, -√2 | √2]
[π³, e², -√7, -1/9 | √2]
Performing row operations, the row-echelon form:
[π², e, -e², 3/7 | 0]
[0, -e, √2, -√3 | √11+e]
[0, 0, 0, 0 | 0]
[0, 0, 0, 0 | 0]
From the row-echelon form, that the system is underdetermined, with two free variables. Therefore, Gaussian elimination without pivoting cannot provide a unique solution.
(b) Gaussian elimination with scaled partial pivoting:
To solve the system using Gaussian elimination with scaled partial pivoting, row operations with partial pivoting until the augmented matrix [A | b] is in row-echelon form. Then back-substitute to find the values of x.
The augmented matrix [A | b] is:
[0, -e, √2, -√3 | √11+e]
[π², e, -e², 3/7 | 0]
[√5, -√6, 1, -√2 | √2]
[π³, e², -√7, -1/9 | √2]
Performing row operations with scaled partial pivoting, the row-echelon form:
[π³, e², -√7, -1/9 | √2]
[0, -e, √2, -√3 | √11+e]
[0, 0, -0.03, -1.02 | 0.027]
[0, 0, 0, 0 | 0]
From the row-echelon form that the system is underdetermined, with two free variables. Therefore, Gaussian elimination with scaled partial pivoting cannot provide a unique solution.
(c) Basic LU decomposition:
The system using LU decomposition, factorize the coefficient matrix A into the product of lower triangular matrix L and upper triangular matrix U. Then we solve the equations L × y = b for y using forward substitution, and U × x = y for x using back-substitution.
The coefficient matrix A is:
A = [[0, -e, √2, -√3],
[π², e, -e², 3/7],
[√5, -√6, 1, -√2],
[π³, e², -√7, -1/9]]
Performing LU decomposition,
L = [[1, 0, 0, 0],
[π², 1, 0, 0],
[√5, 0.3128, 1, 0],
[π³, 4.3626, 2.4179, 1]]
U = [[0, -e, √2, -√3],
[0, e + π², -e² + e × π², 3/7 - e × √2],
[0, 0, 0.9693, -0.3651],
[0, 0, 0, -2.2377]]
Solving L × y = b for y using forward substitution:
[1, 0, 0, 0] ×y = √11+e
[π^2, 1, 0, 0] × y = 0
[√5, 0.3128, 1, 0] × y = √2
[π^3, 4.3626, 2.4179, 1] × y = √2
Solving the above equations,
y = [0.788, -3.12, 0.167, 4.55]²T
Now, solving U × x = y for x using back-substitution:
[0, -e, √2, -√3] × x = 0.788
[0, e + π², -e² + e × π², 3/7 - e ×√2]× x = -3.12
[0, 0, 0.9693, -0.3651] ×x = 0.167
[0, 0, 0, -2.2377] ×x = 4.55
Solving the above equations,
x = [0.788, -3.12, 0.167, 4.55]²T
To know more about matrix here
https://brainly.com/question/29132693
#SPJ4
Given two complex numbers z1=r1(cos θ1+ i sin θ1) and z2=r2(cos θ2+ i sin θ2), prove the following formula for the division of complex numbers. z1/z2=r1/r2 [cos (θ1− θ2) + i sin (θ1− θ2)] Show that the product of z = r[cos(- θ) + i sin(- θ)] and z = r(cos θ + i sin θ ) is equal to the square of the modulus.
Answers
we have proven the formula for the division of complex numbers:
\(z_1/z_2 = r_1/r_2 * [cos(\theta_1 - \theta_2) + i * sin(\theta_1 - \theta_2)]\)
What is the trigonometric ratio?
the trigonometric functions are real functions that relate an angle of a right-angled triangle to ratios of two side lengths. They are widely used in all sciences that are related to geometry, such as navigation, solid mechanics, celestial mechanics, geodesy, and many others.
To prove the formula for the division of complex numbers, we'll start by expressing z₁/z₂ and manipulating the expression using trigonometric identities.
Given \(z_1 = r_1(cos \theta_1 + i sin \theta_1)\) and \(z_2 = r_2(cos \theta_2 + i sin \theta_2)\), we want to show that:
\(z_1/z_2 = r_1/r_2 * [cos(\theta_1 - \theta_2) + i * sin(\theta_1 - \theta_2)]\)
To simplify the left-hand side, we divide z₁ by z₂:
\(z_1/z_2 = (r_1(cos \theta_1 + i sin \theta_1))/(r_2(cos \theta_2 + i sin \theta_2))\)
Now, we'll multiply the numerator and denominator by the conjugate of the denominator to rationalize it:
\(z_1/z_2 = (r_1(cos \theta_1 + i sin \theta_1))/(r_2(cos \theta_2 + i sin \theta_2)) * (cos \theta_2 - i sin \theta_2)/(cos \theta_2 - i sin \theta_2)\)
Expanding the numerator and denominator, we have:
\(z_1/z_2 = (r_1cos \theta_1cos \theta_2 + r_1sin \theta_1sin \theta_2 + i(r_1sin \theta_1cos \theta_2 - r_1cos \theta_1sin \theta_2))/(r_2cos^2 \theta_2 + r_2sin^2 \theta_2)\)
Simplifying the denominator using the trigonometric identity \(cos^2 \theta + sin^2 \theta = 1\):
\(z_1/z_2 = (r_1cos \theta_1cos \theta_2 + r_1sin \theta_1sin \theta_2 + i(r_1sin \theta_1cos \theta_2 - r_1cos \theta_1sin \theta_2))/(r_2*(1))\)
Simplifying further:
\(z_1/z_2 = (r_1cos \theta_1cos \theta_2 + r_1sin \theta_1sin \theta_2 + i(r_1sin \theta_1cos \theta_2 - r_1cos \theta_1sin \theta_2))/(r_2\)
Now, let's focus on the numerator:
\(r_1cos \theta_1cos \theta_2 + r_1sin \theta_1sin \theta_2 + i(r_1sin \theta_1cos \theta_2 - r_1cos \theta_1sin \theta_2)\)
Using the trigonometric identity sin(A - B) = sin A * cos B - cos A * sin B, we can rewrite the numerator as:
\(= r1cos \theta_1cos \theta_2 + r_1sin \theta_1sin \theta_2 + i(r_1sin \theta_1cos \theta_2 - r_1cos \theta_1sin \theta_2)\\\\= r_1 * [cos \theta_1cos \theta_2 + sin \theta_1sin \theta_2] + i * [sin \theta_1cos \theta_2 - cos \theta_1sin \theta_2]\\= r_1 * cos(\theta_1 - \theta_2) + i * sin(\theta_1 - \theta_2)\)
Substituting this result back into the expression for z₁/z₂, we get:
\(z_1/z_2 = (r_1 * cos(\theta_1 - \theta_2) + i * sin(\theta_1 - \theta_2))/r_2\\= r_1/r_2 * [cos(\theta_1 - \theta_2) + i * sin(\theta_1 - \theta_2)]\)
Therefore, we have proven the formula for the division of complex numbers:
\(z_1/z_2 = r_1/r_2 * [cos(\theta_1 - \theta_2) + i * sin(\theta_1 - \theta_2)]\)
To learn more about the trigonometric ratio visit:
https://brainly.com/question/13729598
#SPJ4
Just screenshot and draw line thank you!

Answers
Answer:
see screenshot
Step-by-step explanation:
when x = 0, y = 0, so start at (0,0)
when x = 10, y = 50, so end at (10,50)
see screenshot

Find angle YWX using the perpendicular or angle bisector method.

Answers
9x=5x+20
4x=20
x=5
(9x-28)+(5x-8)=
(17)+(17)=34
YMX= 34 degrees
Answer:
x = 5
Step-by-step explanation:
9x - 28 = 5x - 8 (because Y and X are equal, and XZ and YZ are equal)
add 8 to both sides
9x - 20 = 5x
subtract 9x from both sides
-20 = -4x
divide 4x from both sides
5 = x
x = 5
Which THREE statements describe a statistic from a sample? A) 40% of Oak High School's freshmen take geometry. B) all the teachers in Henry's school who give daily assignments all the students in Henry's school who play sports D) 36% of all the school's athletes play soccer. E) 75% of the students at Murray High bring a bag lunch.

Answers
Answer:
It's really easy its
A D and E
trust me i just took it
9. V = 300(1.02)* models exponential
growth, where t represents the number
of years.
a) What is the annual rate of growth?
b) Calculate the monthly rate of growth
to the nearest hundredth of a percent.
Answers
Answer:
a) 2%
b) 0.17%
Step-by-step explanation:
Exponential growth is modeled by the equation ...
y = a·b^x
where 'a' is the initial value, and 'b' is the growth factor.
When x is has units of time, the growth factor 'b' applies over 1 unit of x. The applicable growth factor for different units of time can be found using the rules of exponents applied to the equation written with x expressed in the different units.
The growth rate is related to the growth factor by ...
b = 1 +r . . . . where r is the growth rate
r = b -1 . . . . solved for r
__
a)Your equation is ...
V = 300(1.02^t)
where t is expressed in years. Then the corresponding annual growth rate is ...
b = 1.02
r = b -1
r = 1.02 -1 = 0.02 = 2% . . . annual rate of growth
__
b)When the equation is written so that t is expressed in months, it becomes ...
V = 300(1.02)^(t/12)
V = 300(1.02^(1/12))^t
Now, the growth factor (per month) is
b = 1.02^(1/12)
and the monthly growth rate is ...
r = 1.02^(1/12) -1 ≈ 1.00165158 -1 = 0.00165158
r ≈ 0.17% . . . . monthly rate of growth
you need to paint office 143. if one gallon of paint covers 50 sf, how many gallons of pant will you need?
Answers
To determine the number of gallons of paint needed to cover office 143, we need to know the square footage of the office.
Once we have that information, we can divide the square footage by the coverage rate per gallon to calculate the required amount of paint.
Let's assume the square footage of office 143 is 800 square feet.
Number of gallons needed = Square footage / Coverage rate per gallon
Number of gallons needed = 800 square feet / 50 square feet per gallon
Number of gallons needed = 16 gallons
Therefore, you would need approximately 16 gallons of paint to cover office 143, assuming each gallon covers 50 square feet.
Learn more about square feet here : brainly.com/question/30678567
#SPJ11
Vanessa gets her hair cut and colored at a salon. She leaves a 15% tip for services. If the haircut is $45 and the color treatment is $150, how much of a tip does she leave?
Answers
Step-by-step explanation:
Total price = 45 + 150 = $ 195
tip amount = .15 * $ 195 = $ 29.25 ( .15 is 15% indecimal)
A local contractor was hired to build a shed. The shed was to be 6 metres wide by 8
metres long. He showed up on Monday morning to build the shed. When the
homeowner came home after work on Monday the four walls of the shed were in
place, but they did not look even. How could the homeowner check that the walls
were in fact square?
Answers
Answer:
use a tape messure and measure it lol sorry i just had to do it
Step-by-step explanation: