Which of the following rational functions is graphed below?
5
10
A. F(X) =
OB. F(x)=
O C. F(x) =
D. F(X) =
(x + 1)
(x + 2)(x-2)
(x+1)
(x-1)(x+2)
2x
x(x - 2)
(x-1)
x(x-2)
ڈے

Answers
Answer:
B. F(x) = (x+1)/(x-1)(x+2)
Step-by-step explanation:
See attached graph. Note how the two vertical lines at x = -2 and 1 match plot B

The following graph is of the rational function \(F(x) = \frac{x+1}{(x-1)(x+2)} \\\)
What are asymptotes?
An asymptote is a straight line that constantly approaches a given curve but does not meet at any infinite distance.
The rational function does not exist at x = 1 and x = -2 ( as observed in graph). Thus, the denominator of the function consist (x-1) and (x+2). It is only in option B, thus it is correct.
Learn more about asymptotes here
https://brainly.com/question/4084552
#SPJ2
Related Questions
6:2:3 last month 24 pairs of boots were sold how many boots all the together were sold last month
Answers
Last month, a total of 72 boots were sold. To calculate the total number of boots sold last month, we need to multiply the number of pairs of boots sold (24) by the ratio 6:2:3. In this ratio, each part represents a fraction of the total number of boots.
In the given ratio, the first part represents 6 out of 11 parts. So, we can calculate the fraction of boots sold by multiplying the first part of the ratio (6) by the total number of parts (11): 6/11 * 24 = 72/11.
Therefore, a total of 72 boots were sold last month.
The ratio 6:2:3 indicates that for every 6 parts of boots sold, there are 2 parts of another type of boots and 3 parts of yet another type. In this case, since we only have information about the first part (24 pairs of boots), we need to find the fraction of the total number of boots that the first part represents.
To calculate this fraction, we multiply the first part (6) by the total number of parts in the ratio (11). This gives us the fraction 6/11, which represents the proportion of boots sold out of the total. Multiplying this fraction by the total number of pairs of boots sold (24) gives us the total number of boots sold last month, which is 72.
Therefore, using the given ratio and the number of pairs of boots sold, we can determine the total number of boots sold by considering the proportion of each type of boots in the ratio.
Learn more about fraction here: brainly.com/question/10354322
#SPJ11
You want to fit a least-squares regression line to the following data {(1, 2), (2, 4),(3, 5),(4, 7)}. Find the equation of the fitted regression line.
Answers
To find the equation of the fitted regression line, we can use the least-squares regression method. In this method, we try to find a line that minimizes the sum of squared residuals between the actual y-values and the predicted y-values. The equation of the fitted regression line can be given by y = mx + b, where m is the slope of the line and b is the y-intercept.
We can find the values of m and b using the following formulas:
$$m = \frac{n\sum xy - \sum x\sum y}{n\sum x^2 - (\sum x)^2}$$ and $$b = \frac{\sum y - m\sum x}{n}$$
where n is the number of data points, x and y are the independent and dependent variables, respectively, and ∑ denotes the sum over all data points. Now, let's use these formulas to find the equation of the fitted regression line for the given data.
The given data are: {(1, 2), (2, 4),(3, 5),(4, 7)}. We can compute the values of n,
∑x, ∑y, ∑xy, and ∑x² as follows:$$n = 4$$$$\
sum x = 1 + 2 + 3 + 4 = 10$$$$\sum y = 2 + 4 + 5 + 7 =
18$$$$\sum xy = (1 × 2) + (2 × 4) + (3 × 5) + (4 × 7)
= 2 + 8 + 15 + 28 = 53$$$$\sum x² = 1 + 4 + 9 + 16 = 30$$
Now, we can substitute these values into the formulas for m and b to get:$$m
= \frac{n\sum xy - \sum x\sum y}{n\sum x^2 - (\sum x)^2}$$$$\qquad
= \frac{(4)(53) - (10)(18)}{(4)(30) - (10)^2}
= \frac{106}{4} = 26.5$$and$$b
= \frac{\sum y - m\sum x}{n}$$$$\qquad
= \frac{18 - (26.5)(10)}{4} = -7.75$$
Therefore, the equation of the fitted regression line is:$$y = mx + b$$$$\qquad = (26.5)x - 7.75$$
learn more about regression line
https://brainly.com/question/732489
#SPJ11
Oscar makes fruit punch to sell from his food truck by mixing 8 parts cranberry juice to 3 parts pineapple juice. How many cups of pineapple juice would Oscar need to mix with 48 cups of cranberry juice to make his punch?
Answers
Answer:
he needs to mix 18 pineapple cups
Step-by-step explanation:
48÷8=6
3×6=18
8-3
48-18
Part A what is the measure of the missing angle in the triangle?

Answers
Answer:
39
Step-by-step explanation:
the interior angles of a triangle equal 180.
180-(51+90)
180- 141 = 39
hope this helps :)
1) a. Write an equation that expresses the first law of thermodynamics in terms of heat and work.
b. Under what conditions will the quantities q and w be negative numbers?
Answers
The first law of thermodynamics is a fundamental principle in physics that states energy cannot be created or destroyed, only converted from one form to another. It can be expressed in terms of heat and work through the equation:
ΔU = q - w
where ΔU represents the change in internal energy of a system, q represents the heat added to the system, and w represents the work done on or by the system.
Now, let's address when the quantities q and w would be negative numbers.
1) When q is negative: This occurs when heat is removed from the system, indicating an energy loss. For example, when a substance is cooled, heat is extracted from it, resulting in a negative value for q.
2) When w is negative: This occurs when work is done on the system, decreasing its energy. For instance, when compressing a gas, work is done on it, leading to a negative value for w.
In both cases, the negative sign indicates a reduction in energy or the transfer of energy from the system to its surroundings.
In summary, the first law of thermodynamics can be expressed as ΔU = q - w, and q and w can be negative numbers when energy is lost from the system through the removal of heat or when work is done on the system.
know more about first law of thermodynamics states.
https://brainly.com/question/31275352
#SPJ11
solve by substitution 6x-4y=18, -x-6y=7
Answers
Answer:
(2,-1.5)
Step-by-step explanation:
6x-4y=18
-x-6y=7
Switch the second equation from standard form to y=mx+b form
-x-6y=7→ -x=7+6y → multiply both sides by -1→ x=-7-6y
Substitute all of the things that equal x into the other equation into x
6x-4y=18→ 6(-7-6y)-4y=18
Simplify
-42-36y-4y=18
Bring - 42 to the other side and add like terms
-42-36y-4y=18→ -40y= 60
Solve for y
y=-1.5
Choose an equation and plug y in it.
-x-6(-1.5)=7
-x+9=7
-x=-2
Multiply both sides by -1
x=2
PLS HELP MEE I HAVE SO MANY MISSING ASSIMENTS HELPPP

Answers
Answer:
21 days
Step-by-step explanation:
To find the answer, we need to find the Least Common Multiple (LCM) of 3 and 7.
The LCM of these two numbers is 21.
find a function whose maclaurin expansion is 1 + x3 + x6 2! + x9 3! + x12 4!
Answers
The function is \(e^{(x^3)}\) whose Maclaurin expansion is 1 + \(x^3\) + \((x^6)\)/2! + \((x^9)\)/3! + \((x^{12} )\)/4! + ...
The Maclaurin series of a given function is represented as a sum of terms with increasing powers of x and decreasing factorials. The Maclaurin series you provided is:
1 + \(x^3\) + \((x^6)\)/2! + \((x^9)\)/3! + \((x^{12} )\)/4! + ...
This series can be rewritten as:
∑ \((x^{(3n)} )/n!\) for n=0 to infinity.
This expansion resembles the Maclaurin series for \(e^x\), which is:
\(e^x\) = ∑ \(x^n\)/n! for n=0 to infinity.
However, in the given series, the powers of x are in multiples of 3. To adjust the standard exponential function to match the provided series, you can use the substitution \(x^3\) = u:
\(e^u\) = ∑ \(u^n\)/n! for n=0 to infinity.
Now, substitute \(x^3\) back for u:
\(e^{(x^3)}\) = ∑ \((x^{(3n)} )/n!\) for n=0 to infinity.
Therefore, the function whose Maclaurin expansion matches the given series is f(x) = \(e^{(x^3)}\).
Know more about the Maclaurin series here :
https://brainly.com/question/31683608
#SPJ11
Eddie Foster packs and seals pens at rate of $0.235 per pack. At the end of his eight-hour
shift, Foster has packed and sealed 480 packs of pens. How much did he earn?
Answers
Answer:
$112.80
Step-by-step explanation:
If he earns $0.235 per pack, and there are 480 packs, then our equation is:
0.235 x 480 = $112.80
The amount of money earned by Eddie for packing and sealing packs of 480 pens is $112.8
What is unitary method?
The method in which first we find the value of one unit and then the value of the required number of units is known as the Unitary Method.
According to the given question.
Amount of money charged by Eddie for packing and sealing a pack of pens = $0.235
Therefore,
The amount of money charged by Eddie for packing and sealing packs of 480 pens
= 480 × $0.235
= $112.8
Hence, the amount of money earned by Eddie for packing and sealing packs of 480 pens is $112.8
Find out more information about unitary method here:
https://brainly.com/question/22056199
#SPJ3
There are 3 green balls, 5 red balls and 2 blue balls in a box. One ball is randomly drawn, replaced and then another ball is drawn.
What is the probability of getting a green ball then a blue ball?
115
12
350
3100
Answers
Answer:
D / 350
Step-by-step explanation:
3/10 x 2/10= 6/100=3/50
so yah!
a colony is a statement far away from the government that rules it true or false
Answers
explanation :
PLS HELP will give brainleist

Answers
Answer:
just substitute the X's
3) 19,7,22,-26
6) 2,-10,-7,-2,-3
7)45,18,72,-54
place them in the y section in order
Are red-black trees an implementation of 2/3 trees?
Answers
Red-black trees are a type of self-balancing binary search tree, and while they are similar in structure and behavior to 2-3 trees, they are not an implementation of 2-3 trees.
2-3 trees and red-black trees are both self-balancing binary search trees, which means that they maintain their balance by automatically adjusting their structure after insertions and deletions. Both types of trees can be used to implement the same operations, such as searching, inserting, and deleting elements in logarithmic time.
However, 2-3 trees have a different structure and use a different balancing strategy than red-black trees. 2-3 trees are composed of nodes with either two or three children, whereas red-black trees are composed of nodes with two children and use color-coded links to balance the tree. While the two types of trees have some similarities, they are not the same thing, and red-black trees are not considered an implementation of 2-3 trees.
To know more on binary search trees
https://brainly.com/question/12946457
#SPJ4
--There is a slight error in the question, answering to the question below--
"Are red-black trees an implementation of 2-3 trees?"
a^2/5 • a^-3
Vvbbbvvbbbbbbnnnnnnnnnnn
Answers
Answer:
A^(2/5) / a^3
Step-by-step explanation:
To simplify the expression A^2/5 • a^-3, we can use the properties of exponents which state that:
a^m • a^n = a^(m+n) (Product Rule)
a^m / a^n = a^(m-n) (Quotient Rule)
Using these properties, we can simplify the expression as follows:
A^2/5 • a^-3 = A^(2/5) / a^3
Therefore, the simplified form of the expression A^2/5 • a^-3 is A^(2/5) / a^3.
Help me please!! Answer question #21 ( the middle question)

Answers
Answer:
i dont know sorry
Step-by-step explanation:
i dont understand i just watch anime all day
Answer:
Free points? idek sorry.
Step-by-step explanation:
Solve for a. Round to the nearest tenth of a degree, if necessary..
Answer: x=
२०
83
92
M
L
Submit Answer
attempt 1 out of 2

Answers
The value of angle x rounded to the nearest tenth of a degree is 53.6°.
How can trigonometric ratios be used to find the angle in a right triangle?
Trigonometric ratios are used to relate the sides of a right triangle to its angles. In a right triangle, one of the angles is always 90 degrees, which is the right angle. The three primary trigonometric ratios are sine, cosine, and tangent, which are defined as follows:
Sine (sin): The sine of an angle is the ratio of the length of the side opposite the angle to the length of the hypotenuse.
Cosine (cos): The cosine of an angle is the ratio of the length of the side adjacent to the angle to the length of the hypotenuse.
Tangent (tan): The tangent of an angle is the ratio of the length of the side opposite the angle to the length of the side adjacent to the angle.
To find the value of an angle in a right triangle, we can use the inverse trigonometric functions, also known as arc functions or anti trigonometric functions. These functions are denoted as \(sin^{-1}\), \(cos^{-1}\) , and \(tan^{-1}\) , and they are used to find the angle whose trigonometric ratio is known.
Finding the value of x :
We can use the trigonometric ratio of sine to solve for x.
sin(x) = opposite/hypotenuse = MN/LN
\(sin(x) = 83/92\)
Taking the inverse sine of both sides:
\(x = sin^{-1}(83/92)\)
Using a calculator, we get:
\(x \approx 53.6^{o}\)
Therefore, the value of x rounded to the nearest tenth of a degree is 53.6°.
To know more about angle visit :
brainly.com/question/28451077
#SPJ1
what is half of half of half of 8?
Answers
Answer:
I believe it is 1
Step-by-step explanation:
half of 8 is 4
half of 4 is 2
half of 2 is 1
Answer:
Step-by-step explanation:
Answer:
Step-by-step explanation:
Find the measure of the arc or angle indicated.

Answers
A student is planning to attend college in 5 years. The student has saved $1,200 and plans to save another $50 per month over the next 60 months. Based on this information about the student’s plan, which statement about the possible choices for a college is true?
Answers
The correct answer choice:
The student would be able to afford the in-state cost for one year at a public 2-year college.
The correct option is D.
What is multiplication?Multiplication is a mathematical arithmetic operation. It is also a process of adding the same types of expression some number of times.
Example - 2 × 3 means 2 is added three times, or 3 is added 2 times.
Given:
A student is planning to attend college in 5 years.
The student has saved $1,200 and plans to save another $50 per month over the next 60 months.
The total savings,
= 1200 + (50 x 60)
= $4200
That is equivalent to the cost of one year at a public 2-year college.
Therefore, the saving amount is equivalent to the cost of one year at a public 2-year college.
To learn more about multiplication;
https://brainly.com/question/19634536
#SPJ1
The table shows the cost per year of attending different types of colleges.
A student is planning to attend college in 5 years. The student has saved $1,200 and plans to save another $50 per month over the next 60 months.
Based on this information about the student's plan, which statement about the possible choices for a college is true?
Answer choices
The student would be able to afford the cost for one year at a private 4-year college.
The student would be able to afford out-of-state cost for half a year at a 4-year public college.
The student would be able to afford in-state cost for half a year at a public 4-year college.
The student would be able to afford in-state cost for one year at a public 2-year college.
How do you find the equation of a line tangent to the curve at point
t=−1 given the parametric equations x=t3+2t and y=t2+t+1?
Answers
The equation of the line tangent to the curve at t = -1 is x + 5y = -2.
To find the equation of the line tangent to the curve defined by the parametric equations x = t^3 + 2t and y = t^2 + t + 1 at the point where t = -1, we need to follow these steps:
Calculate the values of x and y at t = -1:
Substitute t = -1 into the parametric equations:
x = (-1)^3 + 2(-1) = -1 - 2 = -3
y = (-1)^2 + (-1) + 1 = 1
So, the point on the curve where t = -1 is (-3, 1).
Find the derivatives of x and y with respect to t:
dx/dt = 3t^2 + 2
dy/dt = 2t + 1
Evaluate the derivatives at t = -1:
dx/dt = 3(-1)^2 + 2 = 3 + 2 = 5
dy/dt = 2(-1) + 1 = -2 + 1 = -1
Use the derivatives to determine the slope of the tangent line at t = -1:
slope = dy/dx = (dy/dt)/(dx/dt) = (-1)/(5) = -1/5
Use the point-slope form of a linear equation to find the equation of the tangent line:
y - y1 = m(x - x1)
Plugging in the values: y - 1 = (-1/5)(x - (-3))
Simplifying: y - 1 = (-1/5)(x + 3)
Multiplying both sides by 5 to eliminate the fraction: 5y - 5 = -x - 3
Rearranging: x + 5y = -2
Know more about derivatives here:
https://brainly.com/question/25324584
#SPJ11
the annual precipitation amounts in a certain mountain range are normally distributed with a mean of 90 inches, and a standard deviation of 14 inches. what is the probability that the mean annual precipitation of a sample of 49 randomly picked years will be less than 92.8 inches?
Answers
The probability that the mean annual precipitation of a sample of 49 randomly picked years will be less than 92.8 inches is, 0.9192
What is standard deviation?
The standard deviation in statistics is a measurement of how much a group of values can vary or be dispersed. A low standard deviation suggests that values are often close to the set's mean, whereas a large standard deviation suggests that values are dispersed over a wider range.
Given: The annual precipitation amounts in a certain mountain range are normally distributed with a mean of 90 inches, and a standard deviation of 14 inches.
z score is given by,
z = (x - μ)/(σ/√n) = (92.8 - 90)/(14/√49) = 2.8/2 = 1.4
The required probability is,
p(z < 1.4) = 0.9192, by standard normal table.
Hence, the probability that the mean annual precipitation of a sample of 49 randomly picked years will be less than 92.8 inches is, 0.9192.
To know more about the standard deviation, click on the link
https://brainly.com/question/475676
#SPJ4
An angle measures 3° more than two times its complement x please explain
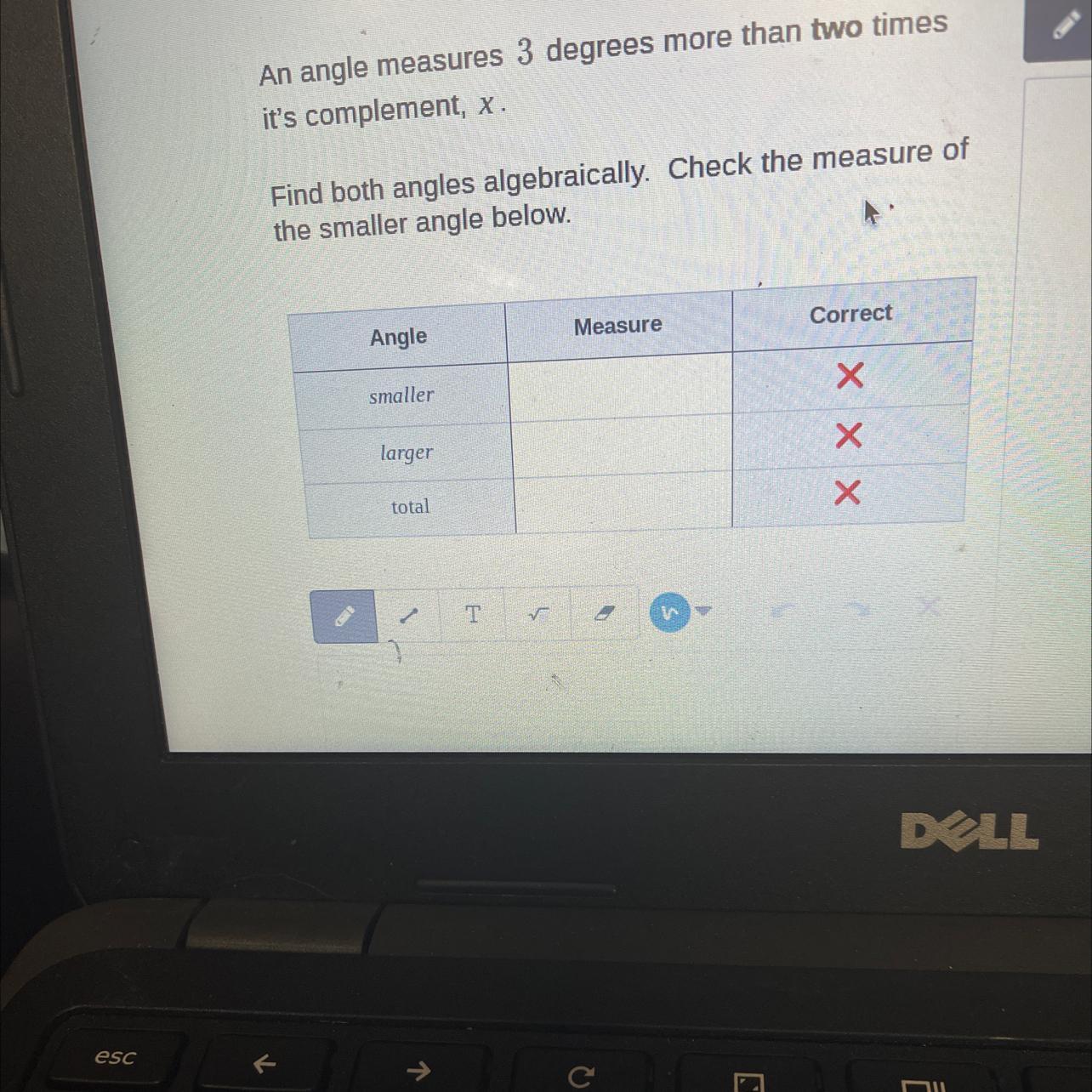
Answers
Solution:
Given that;
An angle measures 3° more than two times its complement x.
Let the larger angle be y
\(x+y=90\degree\)The angle measures 3° more than two times its complement, i.e.
\(y=(2x+3)\degree\)Then,
\(\begin{gathered} x+y=90\degree \\ x+(2x+3)\degree=90\degree \\ x\degree+2x\degree+3\degree=90\degree \\ 3x\degree=90\degree-3\degree \\ 3x=87\degree \\ x=\frac{87\degree}{3} \\ x=29\degree \end{gathered}\)The smaller angle, x is 29 degrees
The larger angle is
\(y=2x+3=2(29)+3=58+3=61\degree\)The larger angle, y is 61 degrees
The total is
\(x+y=29+61=90\degree\)The total is 90 degrees.
A quadratic equation has exactly one real number solution. Which is the value of its discriminant?
Answers
The value of the discriminant when a quadratic equation has exactly one real number solution is zero.
If a quadratic equation has exactly one real number solution, it means that the discriminant of the quadratic equation is equal to zero. The discriminant is a value calculated from the coefficients of the quadratic equation and determines the nature of its solutions.
For a quadratic equation of the form ax^2 + bx + c = 0, the discriminant (D) is given by the formula:
D = b^2 - 4ac
When a quadratic equation has exactly one real number solution, it means that the discriminant is equal to zero:
D = 0
Setting the discriminant to zero, we can solve for the value of the discriminant:
b^2 - 4ac = 0
Therefore, the value of the discriminant when a quadratic equation has exactly one real number solution is zero.
for such more question on quadratic equation
https://brainly.com/question/17482667
#SPJ8
1
Which expression is equivalent to
( 16x9y-12)
?
-

Answers
Hope this helps
PLEASE HELP ME SOLVE
Seacausus stadium has a seating capacity for 25,000 spectators. The stadium has 25 exits and can be vacated in 20 minutes. The time taken to exit the stadium varies directly with the number of spectators and inversely with the number of exits. Determine the time taken for 21,000 spectators to vacate the stadium, if only 15 exits are functional.
Answers
The time taken for 21000 spectators to vacate the stadium , if only 15 exits are functional is 28 minutes .
In the question ,
it is given that
the time taken to vacate the stadium = 20 minutes
number of exits = 25 exits
capacity of the stadium = 25000 spectators .
given that ,
time taken to exit the stadium varies directly with number of spectators and inversely with the number of exits .
time taken ∝ number of spectators ∝ 1/number of exits .
to remove the proportionality sign , we write the constant
time taken = k * (number of spectators)/(number of exits) .
20 = k * 25000/25
20 = k * 1000
k = 20/1000
k = 2/100
k = 1/50 = 0.02
So, to find the time taken for 21,000 spectators to vacate the stadium, if only 15 exits are functional , we use the formula
time taken = (0.02)*(21000/15)
= 0.02*1400
= 28
Therefore , The time taken for 21000 spectators to vacate the stadium , if only 15 exits are functional is 28 minutes .
Learn more about Equation here
https://brainly.com/question/23633125
#SPJ1
f(x) = 2x2 - 1 What is f(x) when x=2 ?
Answers
Answer:
7
Step-by-step explanation:
To evaluate, substitute x = 2 into f(x), that is
f(2)= 2(2)² - 1 = 2(4) - 1 = 8 - 1 = 7
graph the equation -3+2y=12
Answers
Answer:
Step-by-step explanation:
Hope this helped.
A brainliest is always appreciated.

Find the slope intercept of the line passing through the points( -3,3) and (-3,-5)
Answers
Answer:
(-3,3) and (-3,-5)
Step-by-step explanation:
Step 1: y2 - y1
x2 - x1
Step 2: Plug In. --> -5 - 3
-3 - (-3)
Step 3: Solve. --> -8
0
Answr: Undefined. Vertical Line on Graph.
Help me with this asp please

Answers
The x-coordinate of the endpoint of the line segment is 2.
The y-coordinate of the endpoint is -6.
To find the x-coordinate of the endpoint of the line segment, we can use the midpoint formula.
Given that one endpoint is at (10, 12) and the midpoint is at (6, 9), we can denote the coordinates of the other endpoint as (x, y).
Using the midpoint formula, we have:
x-coordinate of the endpoint = 2 * x-coordinate of the midpoint - x-coordinate of the known endpoint
x = 2 * 6 - 10
x = 12 - 10
x = 2
To find the y-coordinate of the endpoint of the line segment, we can use the midpoint formula. We know that the midpoint of the line segment is (6, 9) and one endpoint is (10, 12).
Let the coordinates of the other endpoint be (x, y). Using the midpoint formula, we can set up the following equation:
(10 + x) / 2 = 6
Simplifying the equation, we have:
10 + x = 12
Subtracting 10 from both sides:
x = 2
Therefore, the x-coordinate of the endpoint is 2. Now, we need to find the y-coordinate. Since we know that the endpoint is (2, y), we can use the given endpoint (10, 12) to find the y-coordinate:
12 + y / 2 = 9
Subtracting 12 from both sides:
y / 2 = -3
Multiplying both sides by 2:
y = -6
For more such questions on line segment
https://brainly.com/question/24778489
#SPJ8
in digging a pipe trench that measures 29 feet long, 2 feet 9 inches wide, and 3 feet 6 inches deep.
How many cubic yards of earth were removed from the site?

Answers
Answer:
10.34
Step-by-step explanation:
converting digits to feet,
3ft 6in = 3.5 ft
2ft 9in = 2.75 ft
now feet to yards
3.5ft = 1.16666667 yards (rounded)
2.75ft = 0.9166666667 yards (rounded)
29ft = 9.66666667 yards (rounded)
multiplying them, you'll get approximately 10.34 cubic yards (rounded), that's the volume.
or you can multiply the digits in feet,
3.5×2.75×29
= 279.125 cubic ft
now to convert to cubic yards from cubic ft,
279.125/3³
= 10.337963..
= 10.34 (rounded to the nearest hundredth)