Which of the following quadrilaterals must have at least one pair of parallel sides?
Check all that apply.
Rectangle, Square, Trapezoid, Parallelogram, Kite, Rhombus.
Explain your answer.
Answers
The quadrilaterals that must have at least one pair of parallel sides include all of the following except trapezoid. This implies Rectangle, Square, Parallelogram, Kite, Rhombus
What is a quadrilateral?A quadrilateral is a four-sided polygon with four edges and four corners in geometry. The word comes from the Latin words quadri, a variant of four, and latus, which means "side." A quadrilateral is a closed shape that has four sides, four vertices, and four angles. It's made by connecting four non-collinear points. The sum of quadrilateral interior angles is always 360 degrees.
A rectangle is a quadrilateral with four right angles in Euclidean plane geometry. It can also be defined as an equiangular quadrilateral because all of its angles are equal; or a parallelogram with a right angle. A square is a rectangle with four equal-length sides.
A parallelogram is a simple quadrilateral with two pairs of parallel sides in Euclidean geometry. A parallelogram's opposite or facing sides are equal in length, and its opposite angles are equal in size.
Learn more about parallelogram on:
https://brainly.com/question/11804181
#SPJ1
Related Questions
solve the inequalities show each solution as an interval on the number line 41-x<17
Answers
The inequality in the expression 41-x < 17 is the less than inequality
The solution to the inequality is x > 24
How to solve the inequality?The inequality is given as:
41-x < 17
Subtract 41 from both sides of the inequality
41 - 41 -x < 17 - 41
Evaluate the difference
-x < -24
Multiply both sides by -1
-1 * -x < -24 * -1
Evaluate the product
x > 24
Hence, the solution to the inequality is x > 24
See attachment for the number line
Read more about inequalities at:
https://brainly.com/question/11234618

Question on a picture

Answers
Answer:
c = 0
Step-by-step explanation:
Step 1: Write equation
15 - 5(4c - 7) = 50
Step 2: Solve for c
Distribute -5: 15 - 20c + 35 = 50Combine like terms: -20c + 50 = 50Subtract 50 on both sides: -20c = 0Divide both sides by -20: c = 0Step 3: Check
Plug in c to verify it's a solution.
15 - 5(4(0) - 7) = 50
15 - 5(-7) = 50
15 + 35 = 50
50 = 50
15 - 20c + 35 = 50
50 - 20c = 50
-20c = 0
x = 0
2 parallelograms. The pre-image is smaller than the image.
How can you tell that this transformation is a dilation?
The figure flipped upside down.
The figure changed size.
The figure completed a half turn.
The figure did not change.
Answers
Answer: The figure changed size.
Step-by-step explanation: Dilations change the sizes of shapes. They can either make them bigger or make them smaller.
What is limit of startfraction 6 minus x over x squared minus 36 endfraction as x approaches 6? negative startfraction 1 over 12 endfraction 0 startfraction 1 over 12 endfraction dne
Answers
Answer:
As x approaches 6:
\( \frac{6 - x}{ {x}^{2} - 36 } = - \frac{x - 6}{(x - 6)(x + 6)} = - \frac{1}{x + 6} = - \frac{1}{6 + 6} = - \frac{1}{12} \)
The limit of the given function as x approaches 6 is -1/12. This is achieved by factoring and revising the original function, and then substituting into the revised function.
Explanation:The student is asking for the limit of the function (6-x) / (x²-36) as x approaches 6. In mathematics, this is a problem of calculus and specifically involves limits. Let's solve this by first factoring the denominator to get (6-x) / ((x-6)(x+6))
By realizing we can revise the numerator as -(x-6), we make it obvious that the limit can be directly computed by substituting x=6 after canceling out the (x-6) terms. The result is -1/12, therefore the limit of the function as x approaches 6 is -1/12.
Learn more about limits here:https://brainly.com/question/37042998
#SPJ11
Five years ago, Alan was thrice as old as Aron. After ten years, Alan will be twice as old as Aron. How old are Alan and Aron?
Answers
Alan will be 50 yrs old and Aron will be 20 yrs old

Aaron had $22 to spend on 4 beakers for his science class. After buying them, Aaron had $2 left. How much did each of the beakers cost?
Answers
Answer:4
Step-by-step explanation:22-4=18-4=14-4=10-4=6=2
asgt 2.2 7 of 77 of 7 items on a number line, a is at 5 and b is at 50. point x is the midpoint. point t is 2/3 of the way from x to b. determine the coordinate of point t. distance of xb =
Answers
On a number line where A is at 5 and B is at 50, and X is the midpoint and T is somewhere between A and B, the coordinates of point T is 15 and the distance of XB is 22.5.
A number line is straight line divided by equal measures that serves as a visual representation of the real numbers.
If on a number line, a is at 5 and b is at 50, then AB = 50 - 5 = 45.
If point X is the midpoint of A and B, then X divides the distance of A to B into two equal parts.
let n = AX = XB
AB = AX + XB
45 = n + n
45 = 2n
n = 22.5
AX = XB = 22.5
If point T is 2/3 of the way from X to B, then
T = 2/3XB
T = 2/3(22.5)
T = 15
Hence, the coordinates of T is at 15 and the distance of XB is 22.5.
Learn more about midpoint here: https://brainly.com/question/5566419
#SPJ4

A book has n typographical errors. Two proofreaders, A and B independently read the book and check for errors. A catches each error with probability p1 independently. Likewise for B, who has probability p2 of catching any given error. Let X1 be the number of typos caught by A,X2 be the number caught by B, and X be the number caught by at least one of the two proofreaders. (a) Find the distribution of X. (b) Find E(X). (c) Assuming that p1=p2=p, find the conditional distribution of X1 given that X1+X2=m.
Answers
The denominator can be calculated as the sum of the probabilities of all possible cases where X1 + X2 = m:
P(X1 + X2 = m) = Σ(P(X1 = k, X2 = m - k)), for k = 0 to m
We obtain the conditional distribution P(X1 = k | X1 + X2 = m) for k = 0 to m.
(a) To find the distribution of X, we can consider the cases where A catches k errors and B catches (X - k) errors, for k = 0 to X. The probability of A catching k errors is given by the binomial distribution:
P(X1 = k) = C(X, k) * p1^k * (1 - p1)^(X - k)
Similarly, the probability of B catching (X - k) errors is:
P(X2 = X - k) = C(X, X - k) * p2^(X - k) * (1 - p2)^(X - (X - k))
Since X is the number caught by at least one of the two proofreaders, the distribution of X is given by the sum of the
probabilities for each k:
P(X = x) = P(X1 = x) + P(X2 = x), for x = 0 to X
(b) To find E(X), we can sum the product of each possible value of X and its corresponding probability:
E(X) = Σ(x * P(X = x)), for x = 0 to X
(c) Assuming p1 = p2 = p, we can find the conditional distribution of X1 given that X1 + X2 = m using the concept of conditional probability. Let's denote X1 + X2 = m as event M.
P(X1 = k | M) = P(X1 = k and X1 + X2 = m) / P(X1 + X2 = m)
To find the numerator, we need to consider the cases where X1 = k and X1 + X2 = m:
P(X1 = k and X1 + X2 = m) = P(X1 = k, X2 = m - k)
Using the same logic as in part (a), we can calculate the probabilities P(X1 = k) and P(X2 = m - k) with p1 = p2 = p.
Finally, the denominator can be calculated as the sum of the probabilities of all possible cases where X1 + X2 = m:
P(X1 + X2 = m) = Σ(P(X1 = k, X2 = m - k)), for k = 0 to m
Thus, we obtain the conditional distribution P(X1 = k | X1 + X2 = m) for k = 0 to m.
To know more about conditional distribution, visit:
https://brainly.com/question/14310262
#SPJ11
Amanda leaves Boston at 10:00 AM and drives to Buffalo, NY, which is 400 miles away. After 4 hours, the traffic causes Amanda to reduce her speed by 20 mph. She stops to rest for two hours, and then arrives in Buffalo at 8:00 PM.
What was Amanda's initial speed?
Answers
Because her initial speed is already above the speed limit. So, the problem is not solvable under the given conditions.
Let's call Amanda's initial speed "s" (in mph). We know that she drove for 4 hours at speed s, and then for the remaining time (which is 6 hours), she drove at speed s - 20 mph.
The total distance of the trip is 400 miles. Using the distance formula:
distance = rate × time
we can write two equations:
First part of the trip:
400 = s × 4
Second part of the trip:
400 = (s - 20) × 6
Now we can solve for s. Starting with the first equation:
400 = s × 4
Dividing both sides by 4 gives:
s = 100
So Amanda's initial speed was 100 mph.
Checking with the second equation:
400 = (s - 20) × 6
Substituting s = 100, we get:
400 = (100 - 20) × 6
400 = 80 × 6
400 = 480
This equation is not true, which means that there must be an error in our calculations. The error is that Amanda cannot possibly have driven at 100 mph for 4 hours and then slowed down to 80 mph for the remaining 6 hours, because her initial speed is already above the speed limit. So, the problem is not solvable under the given conditions.
Learn more about initial speed Visit: brainly.com/question/29345000
#SPJ4
2(4 plus 2x) > 5x plus 5
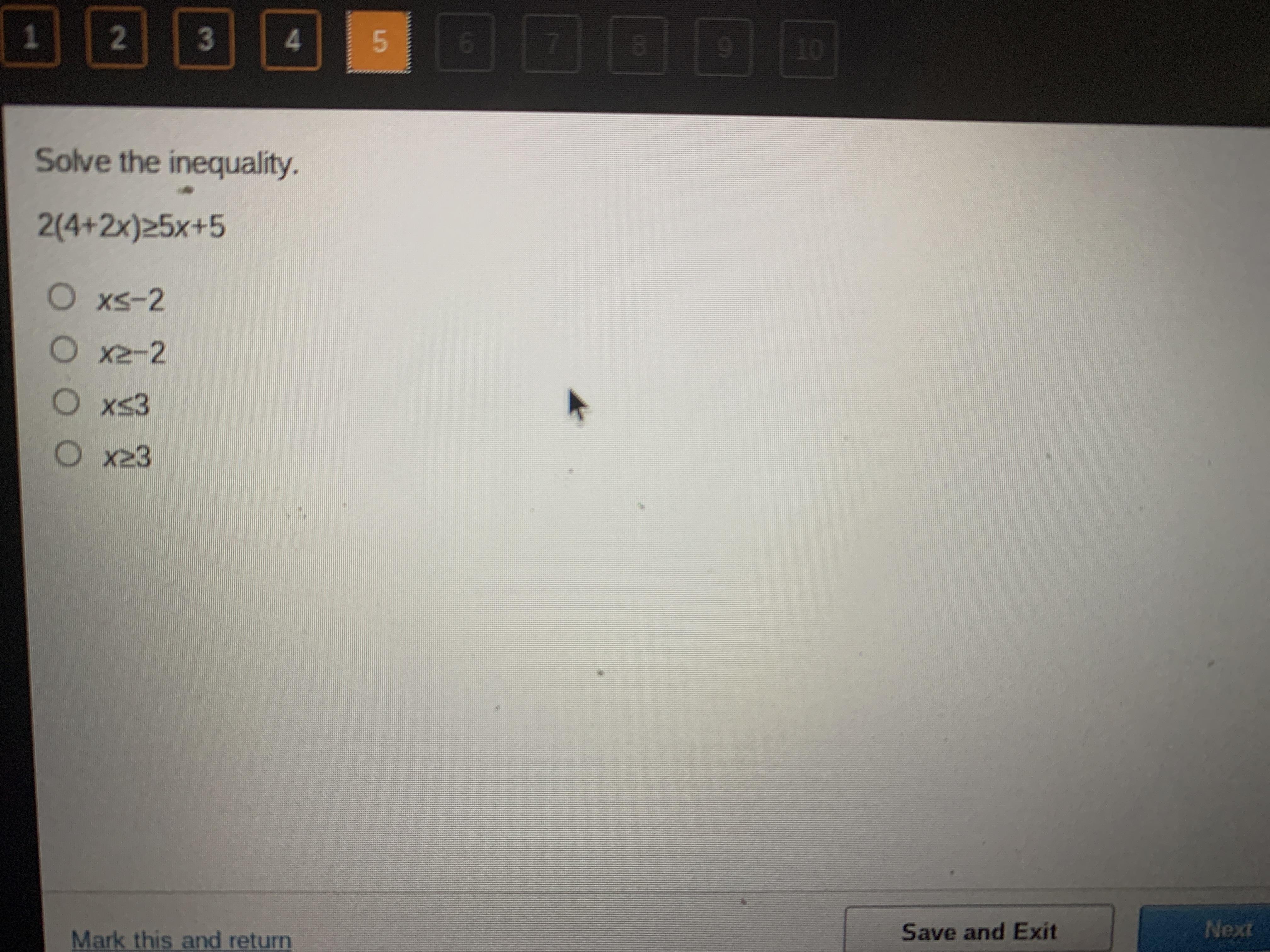
Answers
Answer:
x ≤3
Step-by-step explanation:
2(4+ 2x)≥ 5x+ 5
distribute
8+4x ≥ 5x+ 5
Subtract 4x from each side
8+4x-4x≥ 5x-4x+ 5
8 ≥ x+ 5
Subtract 5 from each side
8-5 ≥ x+ 5-5
3 ≥ x
x ≤3
Answer:
x ≤3
Step-by-step explanation:
Find the area of ABC with vertices A(4, -3) B(9,-3) , and C(10, −11)
Answers
The area of triangle ABC with vertices is 22 square units
How to find the area of ABC with vertices?The vertices are given as:
A(4, -3) B(9,-3) , and C(10, −11)
The area of the triangle is calculated using
Area = 0.5 * |Ax(By - Cy) + Bx(Ay - Cy) + Cx(Ay - By)|
This gives
Area = 0.5 * |4 * (-3 + 11) + 9 * (-3 + 11) + 10 * (-3 - 3)|
Evaluate the sum of products
Area = 0.5 * |44|
Remove the absolute bracket
Area = 0.5 * 44
Evaluate
Area = 22
Hence, the area of ABC with vertices is 22 square units
Read more about areas at:
https://brainly.com/question/22972014
#SPJ1
Alice’s dog eats 9/4 pounds of dog food each day. How much dog food will the dog eat in 30 days?
135 pounds
135/2 pounds
135/4 pounds
135/9 pounds
Answers
Answer:
135/2
Step-by-step explanation:
In 1 day the dog eats 9/4 lbs
In 30 days the dog eats (9/4) * 30 lbs
= (9 * 30) / 4
= 135/2
4/5 + 9/10 what is this answer?
Answers
0.8+.9=1.7
\(\boldsymbol{\sf{\dfrac{4}{5}+\dfrac{9}{10} } }\)
The least common multiple of 5 and 10 is 10. Convert 4/5 and 9/10 to fractions with denominators of 10.
\(\boldsymbol{\sf{\dfrac{4\times2}{5\times2}+\dfrac{9}{10} \ \ \to \ \ Simplify }}\)
\(\boldsymbol{\sf{ \dfrac{8}{10}+\dfrac{9}{10} }}\)
Since 8/10 and 9/10 have the same denominator, join their numerators to add them.
\(\boldsymbol{ \sf{\dfrac{8+9}{10} \ \to \ \ Add }}\)
Simplify
\(\boldsymbol{\sf{ \dfrac{17}{10}= }}\boxed{\boldsymbol{\sf{1\frac{7}{10} }}}\)
an experiment involves selecting a random sample of 256 middle managers for study. one item of interest is their annual incomes. the sample mean is computed to be $35,420.00. if the population standard deviation is $2,150.00, what is the standard error of the mean? rev: 12 23 2020 qc cs-245219 multiple choice $134.38 $144.61 $2,150.00 $8.40
Answers
The standard error of the mean for a sample of 256 middle managers, with a population standard deviation of $2,150.00 and a sample mean of $35,420.00, is approximately $134.38.
The standard error of the mean can be calculated using the formula: standard error = population standard deviation / square root of sample size.
Population standard deviation (σ) = $2,150.00
Sample size (n) = 256
Substituting these values into the formula, we can calculate the standard error of the mean:
Standard error = $2,150.00 / √256
Standard error ≈ $2,150.00 / 16
Standard error ≈ $134.38
Therefore, the standard error of the mean is approximately $134.38.
To know more about standard error refer here
https://brainly.com/question/15119664#
#SPJ11
Because pH affects the reaction, a student carefully creates a suitable aqueous solvent for the reaction. After bubbling CO2 through the solution, he checks the pH and is surprised to find that it is not the same as the original value. What is the most likely cause for this
Answers
The most likely cause for the change in pH after bubbling CO2 through the solution is the formation of carbonic acid.
When CO2 is bubbled through an aqueous solution, it can react with water to form carbonic acid (H2CO3). This reaction occurs due to the dissolution of CO2 in water, which undergoes a chemical equilibrium process. Carbonic acid is a weak acid that can release hydrogen ions (H+) into the solution, thus lowering the pH. The presence of carbonic acid lowers the pH value compared to the original pH of the solvent.
This phenomenon is commonly observed when CO2 is dissolved in water, such as in carbonated beverages. The carbonic acid formed from the reaction with CO2 contributes to the acidic properties of the solution. Therefore, the most likely cause for the change in pH after bubbling CO2 through the solution is the formation of carbonic acid, leading to a decrease in pH.
Learn more about pH here:
https://brainly.com/question/2288405
#SPJ11
15% markdown, 24.30 regular price, sale price?
Please i need help
Answers
PLS HELP! (it will only let me do 31 points :() but you get brainliest.
Explain how to determine the angle measurement for this angle.

Answers
Answer:
107, there is two lines after that so 108 109 and the last line is 110 so your answer will be 107 degrees.
Step-by-step explanation:
Answer:
\(\Large \boxed{\sf 107\°}\)
Step-by-step explanation:
The line is in between 106° and 108° so it is 107°

Elliott Farms has a silo for storage. The silo is a right circular cylinder topped by a right circular cone, both having the same radius. The height of the cone is half the height of the cylinder. The diameter of the base of the silo is 10 meters and the height of the entire silo is 27 meters. What is the volume, in cubic meters, of the silo
Answers
the volume of the silo is approximately 11,657.88 cubic meters.
To find the volume of the silo, we need to calculate the volumes of the cylinder and the cone separately, and then add them together.
The radius of the base of the silo is half the diameter, so it's 10 meters / 2 = 5 meters.
The height of the cylinder is given as 27 meters. Since the height of the cone is half the height of the cylinder, the height of the cone is 27 meters / 2 = 13.5 meters.
The volume of a cylinder is calculated using the formula:
Volume of Cylinder = π * radius^2 * height
Plugging in the values, we get:
Volume of Cylinder = π * 5^2 * 27 = 3375π cubic meters (approximately 10,598.07 cubic meters)
The volume of a cone is calculated using the formula:
Volume of Cone = (1/3) * π * radius^2 * height
Plugging in the values, we get:
Volume of Cone = (1/3) * π * 5^2 * 13.5 = 337.5π cubic meters (approximately 1059.81 cubic meters)
Adding the volumes of the cylinder and the cone, we get:
Volume of Silo = 3375π + 337.5π = 3712.5π cubic meters (approximately 11,657.88 cubic meters)
To know more about diameter visit:
brainly.com/question/31445584
#SPJ11
the error of posting $50 as $500 can be detected by
Answers
The error of posting $50 as $500 can be detected by comparing the recorded amount to the expected amount. Here are the steps to detect this error:
1. Calculate the expected amount: Determine the correct amount that should have been posted. In this case, the expected amount is $50.
2. Compare the recorded amount with the expected amount: Check the posted amount and compare it to the expected amount. If the recorded amount shows $500 instead of $50, then an error has occurred.
3. Identify the discrepancy: Recognize that the recorded amount of $500 is significantly higher than the expected amount of $50.
4. Investigate the source of the error: Look for the cause of the error. It could be a data entry mistake, a typo, or a misunderstanding.
5. Take corrective actions: Once the error is detected, rectify it by posting the correct amount of $50. Additionally, ensure that the source of the error is addressed to prevent similar mistakes in the future.
By following these steps, the error of posting $50 as $500 can be detected, corrected, and prevented from happening again.
Learn more about error-detection here:
brainly.com/question/14974469
#SPJ11
Part A
Fill in the blank question.
SHIPPING The U.S. Department of Commerce regulates how much the actual weight of a package can vary from its labeled weight. A package with a labeled weight of 9.4 pounds can have an actual weight that is plus or minus 0.22 pound.
Part A
Write an absolute value equation to represent the maximum and minimum acceptable weights of the package. Let x be the actual weight of the package.
Answers
The simplified value of the maximum weight is 9.62 and the minimum weight is 9.18. Also the function for the maximum and minimum weight is y + x and y - x
Here,
Given that, A package with a labeled weight of 9.4 pounds can have an actual weight plus or minus 0.22 pounds.
Let the weight labeled be y and the actual weight be x
Weight = y ± x
Maximum weight = y + x
Minimum weight = y - x
Weight = 9.4 ± 0.22
Now,
Maximum weight = 9.4 + 0.22 = 9.62 pounds
Minimum weight = 9.4 - 0.22 = 9.18 pounds
Thus, the simplified value of the maximum weight is 9.62 and the minimum weight is 9.18. Also, the function for the maximum and minimum weight is y + x and y - x
Learn more about algebraic expression here:
https://brainly.com/question/953809
#SPJ1
36x'ys
26 Which expression is equivalent to
(3xy)
for all values of x and y where the expression is
defined?
Answers
The expression (3xy) is an algebraic expression
The equivalent expressions of (3xy) are (6xy)/2 and (9xy)/3
How to determine the equivalent expression?The expression is given as:
(3xy)
Multiply by 2/2
(3xy) = (6xy)/2
Multiply by 3/3
(3xy) = (9xy)/3
The above products means that, we multiply the expression by 1 (i.e. n/n) to get an equivalent expression
Hence, the equivalent expressions of (3xy) are (6xy)/2 and (9xy)/3
Read more about equivalent expressions at:
https://brainly.com/question/2972832
Jackson has a points card for a movie theater.
He receives 45 rewards points just for signing up.
He earns 9.5 points for each visit to the movie theater.
He needs 102 points for a free movie ticket.
Write and solve an equation which can be used to determine xx, the number of visits Jackson must make to earn a free movie ticket.
Equation:
Answer: x =

Answers
The linear equation represents the total number of visits Jackson must make to earn a free movie ticket is 9.5x + 45 = 102 and the total number of visits to the movie theater he must make is 6.
Given :
Jackson has a points card for a movie theater. He receives 45 rewards points just for signing up. He earns 9.5 points for each visit to the movie theater. He needs 102 points for a free movie ticket.The following steps can be used in order to determine the number of visits Jackson must make to earn a free movie ticket:
Step 1 - Let the total number of visits to the movie theater be 'x'.
Step 2 - So, the linear equation represents the total number of visits Jackson must make to earn a free movie ticket is:
9.5x + 45 = 102
Step 3 - Simplify the above linear equation.
9.5x = 57
x = 6
For more information, refer to the link given below:
https://brainly.com/question/2263981
Function or not?
Please help me



Answers
Answer:
Function Not a function
not a Function function
pg 2
B- explanation is that 2 inputs dont have the same output 8-1, 8-1,4-1,3-1
pg 3
1. yes; -5 is not in the set
2. yes; 2 is not in the set
3. no; .75 is 3/4
4. no; -4 is already in the set
Normal probability distribution is applied to: A. a subjective random variable B. a discrete random variable C. any random variable D. a continuous random variable
Answers
Normal probability distribution is applied to a continuous random variable. The correct option is D.
The normal probability distribution, also known as the Gaussian distribution, is a probability distribution that is commonly used in statistics and probability theory. It is a continuous probability distribution that is often used to model the behavior of a wide range of variables, such as physical measurements like height, weight, and temperature.
The normal distribution is characterized by two parameters: the mean (μ) and the standard deviation (σ). It is a bell-shaped curve that is symmetrical around the mean, with the highest point of the curve being located at the mean. The standard deviation determines the width of the curve, and 68% of the data falls within one standard deviation of the mean, while 95% falls within two standard deviations.
The normal distribution is widely used in statistical inference and hypothesis testing, as many test statistics are approximately normally distributed under certain conditions. It is also used in modeling various phenomena, including financial markets, population growth, and natural phenomena like earthquakes and weather patterns.
Overall, the normal probability distribution is a powerful tool for modeling and analyzing a wide range of continuous random variables in a variety of fields.
To learn more about continuous random variable refer here:
https://brainly.com/question/17238189
#SPJ11
Darlene has a job babysitting. On the first day, she made x dollars. On the 2nd day, she made three times the amount, and on the third day, she made $6 more than the first day. How much money did Darlene make if he made $30 the first day?
Answers
2. Write an inequality statement whose solution is an empty set.
3. Write an inequality statement whose solution is some but not all real numbers. Graph the solution on a number line.
4. Write an inequality statement whose solution is all real numbers. Graph the solution on a number line.
5. Write an inequality statement whose solution is exactly one number. Graph the solution on a number line.
Answers
The inequality statements are 1 < 0, x > 0, x = x and x = 5
How to determine the inequality statementsAn empty set
An empty set is a set with no elements.
An inequality statement with no solutions results in an empty set.
One example of an inequality statement with no solutions is 1 < 0.
Some solution but not all real numbers
An inequality statement whose solution is some but not all real numbers is x > 0.
The solution set is the set of all positive real numbers, excluding 0.
The number line is represented as follows
|------------------------------------| 0 |----------------------------- |
All real numbers
A statement whose solution is all real numbers is x = x
The solution set is the set of all real numbers
The number line is represented as follows
|--------------------------- | ... | -2 | -1 | 0 | 1 | 2 | ... |
Exactly one number
A statement whose solution is exactly one number is x = 5.
The solution set is the set containing only the number 5
The number line is represented as follows
|--------------------------- | ... | 4 | ... |
Read more about inequality at
https://brainly.com/question/25275758
#SPJ1
4. In how many ways can 5 men and 7 women be seated in a row so that no two men are next to each other? You must justify your answer.
Answers
Answer:
3628800 ways if the women are always required to stand together.
To solve this problem, we can consider the number of ways to arrange the women and men separately, and then multiply the results together.
First, let's consider the arrangement of the women. Since no two men can be seated next to each other, the women must be seated in between the men. We can think of the 5 men as creating 6 "gaps" where the women can be seated (one gap before the first man, one between each pair of men, and one after the last man).
Out of these 6 gaps, we need to choose 7 gaps for the 7 women to sit in. This can be done in "6 choose 7" ways, which is equal to the binomial coefficient C(6, 7) = 6!/[(7!(6-7)!)] = 6.
Next, let's consider the arrangement of the 5 men. Once the women are seated in the chosen gaps, the men can be placed in the remaining gaps. Since there are 5 men, this can be done in "5 factorial" (5!) ways.
Therefore, the total number of ways to seat the 5 men and 7 women is 6 * 5! = 6 * 120 = 720.
There are 720 ways to seat the 5 men and 7 women in a row such that no two men are next to each other.
To know more about arrangement visit
https://brainly.com/question/1427391
#SPJ11
Determine the implied domain of the following function. Express your answer in interval notation.

Answers
Answer:
(-♾, ♾)
Step-by-step explanation:
A quadratic can accept any real x value. So the domain is All Real Numbers. This in interval notation is
(-♾, ♾)
This is read as negative infinity to positive infinity
The implied domain of g(x) = -2x² + 1 is (-∞, +∞), indicating that the function is defined for all real values of x.
To determine the implied domain of the function g(x) = -2x² + 1, we need to identify the set of all possible values for x that make the function defined and meaningful.
In this case, since the function is a quadratic polynomial, there are no restrictions on the input values of x. The function is defined for all real numbers.
Therefore, the implied domain of the function g(x) = -2x² + 1 is the set of all real numbers, which can be expressed in interval notation as (-∞, +∞).
This interval notation indicates that there are no specific limitations or exclusions on the values of x for the function. It includes all real numbers from negative infinity to positive infinity.
To learn more about function click on,
https://brainly.com/question/31397942
#SPJ2
I DONT GET THIS I REALLY NEED HELP

Answers
Answer: it’s c
Step-by-step explanation:
-5х + 4 = 3х - 12
math is my worst subject
Answers
Answer:
x=1
Step-by-step explanation:
-5x-3x = - 12-4
-8x=-16 multiply that by -8
x=2
Answer:
2
Step-by-step explanation:
Step 1:
- 5x + 4 = 3x - 12 Equation
Step 2:
4 = 8x - 12 Add 5x on both sides
Step 3:
16 = 8x Add 12 on both sides
Step 4:
x = 16 ÷ 8 Divide
Answer:
x = 2
Hope This Helps :)