Which of the following is equivalent to 2/5 x 3/8?
A. 3/8 / 2/5
B. 2/5 / 3/8
C. 2/5 / 8/3
D. 5/2 / 8/3
Answers
Explanation:- 2/5 x 3/8 = 0.15
2/5 / 8/3 = 0.15
Related Questions
(c) Show that for the Legendre polynomials Pn the following holds for all n EN: (n+1) Pn+1(x) - (2n+1)xP(x) +nPn-1(x) = (2n +1) Pn(x) Hint: Bonnet's recursion formula [6]
Answers
The Legendre polynomials Pn satisfy the following recursion formula:(n+1) Pn+1(x) - (2n+1)xP(x) +nPn-1(x) = (2n +1) Pn(x). This can be shown using Bonnet's recursion formula, which states that xPn(x) = (n+1)Pn+1(x) + nPn-1(x).
To prove the above formula, we can use Bonnet's recursion formula to rewrite the left-hand side as (n+1) Pn+1(x) - (2n+1)xP(x) +nPn-1(x) = (n+1) Pn+1(x) + nPn-1(x) - (2n+1)xP(x). We can then combine the first two terms on the right-hand side using the fact that the Legendre polynomials are orthogonal, which means that ∫ Pn(x)Pm(x)dx = 0 if n ≠ m. In this case, we have n = n+1 and m = n-1, so the integral of Pn+1(x)Pn-1(x) over the interval [-1, 1] is zero. This means that the first two terms on the right-hand side cancel out, leaving us with (n+1) Pn+1(x) - (2n+1)xP(x) +nPn-1(x) = - (2n+1)xP(x). We can then factor out a -1 from the right-hand side to get (n+1) Pn+1(x) - (2n+1)xP(x) +nPn-1(x) = - (2n+1)xP(x) = (2n +1) Pn(x). This completes the proof.
To know more about recursion formula here : brainly.com/question/1470853
#SPJ11
the numbers 1447, 1005, and 1231 have something in common: each is a 4-digit number beginning with 1 that has exactly two identical digits. how many such numbers are there?
Answers
If each is a 4-digit number beginning with 1 that has exactly two identical digits , then there are 432 such numbers .
In the question ,
Suppose that the two identical digits are both 1.
and since the thousands digit must be 1, only one of the other three digits can be 1. This means that the possible forms for the required numbers are
11xy , 1x1y , 1xy1 ,
Because the number must have exactly two identical digits, x ≠ y, x ≠ 1, and y ≠ 1.
Hence, Of this form there are 3 × 9 × 8 = 216 numbers .
Now suppose that two identical digits are not 1 , we will have the following possibilities:
1xxy , 1xyx , 1yxx
Again, x ≠ y , x ≠ 1 , and y ≠ 1 .
Of this form there are 3 × 9 × 8 = 216 numbers .
So , the total numbers are 216 + 216 = 432 .
Therefore , the total numbers are 432 .
Learn more about Numbers here
https://brainly.com/question/13220269
#SPJ4
Factor completely: 3x^6 – 11x^5 – 20x^4
Answers
Answer:
x^4 ⋅ (x−5)⋅(3x+4)
Step-by-step explanation:
Answer:
322x
Step-by-step explanation:
if you do 3·3·3·3·3·3 you would get 729
then you would do 11·11·11·11·11 you would get 161051
finally you would do 20·20·20·20 to get 160000
finally you would subtract all those together to get 322 then you would just add the x to get the final answer of 322x
what type of environment did the aboriginals live in?
individual
community
solo
Answers
Answer:
Community
Step-by-step explanation:
did it on edge
The word "and" in probability implies that we use the ____ rule.
A. Subtraction
B. Division
C. Addition
D. Multiplication
Answers
The word "and" in probability implies that we use the Multiplication rule.
The correct option is Option D.
What is the Multiplication Rule of Probability?The likelihood of both events A and B occurring, in accordance with the probability multiplication rule, is equal to the product of the probability of B occurring and the conditional probability of event A occurring given that event B occurs.
The relationship between two events is explained by the probability multiplication rule.
Set A∩B represents the events in which both events A and B have occurred for two events A and B related to a sample space S. Consequently, (A∩B) indicates that occurrences A and B happened at the same time. You can write the event A∩B as AB. Using the characteristics of conditional probability, the likelihood of event AB is calculated.
To learn more about Probability visit:
https://brainly.com/question/29564879
#SPJ4
Simplify. 3 1/2+1/8 im not sure what this is
Answers
Answer:
125/8
is the final answer
Step-by-step explanation:
1.transform the expression
2.calculate
3.(final answer)
Answer:
I Believe the answer is either 3 5/8 or 29/8
Step-by-step explanation:
You have to find the most common denominator which for 1/2 and 1/8 is 8 and then you would do 1/2 1*3 and 2*4 to get 4/8 add them together for 5/8 then would would either add 24/8 to equal the 3 or you would leave the three by itself (depends on what your teacher says for simplification)
As for defining simplification it is solving the problem best you can with the information you are given.
A test to detect an infection gives a positive result 98% of the time when an infection is present. It is 97% accurate when an infection is not present.
Answers
Answer:
false negatives - 2%
false positives - 3%
Step-by-step explanation:
Here is the complete question :
A test to detect an infection gives a positive result 98% of the time when an infection is present. It is 97% accurate when an infection is not present.
% of results will be false negatives, and % of results will be false positives.
False negative means a negative result which in actuality it is positive
False negative = 100% - percent of positive result
100% - 98% = 2%
False positive result means a positive result which in actuality is negative
False positive = 100% - percent of false positive
100 - 97 = 3%
100 more points Help asap!
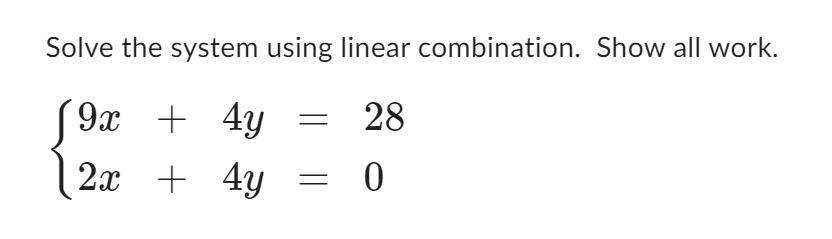



Answers
The answers to the questions on linear combination have been solved below
How to solve the linear combination1. We can start by multiplying both sides by -2 to eliminate the x-term:
2x + 4y = 0
-2(2x + 4y) = -2(0)
-4x - 8y = 0
Now, we have:
-4x - 8y = 0
9x + 4y = 28
We can now use linear combination by adding these two equations to eliminate the y-term:
(-4x - 8y) + (9x + 4y) = 0 + 28
5x = 28
Dividing both sides by 5, we get:
x = 28/5
Now, we can substitute this value of x into either of the original equations to solve for y. Let's use the second equation:
2x + 4y = 0
2(28/5) + 4y = 0
56/5 + 4y = 0
4y = -56/5
y = -14/5
Therefore, the solution to the system of equations is:
x = 28/5
y = -14/5
We can check that these values satisfy both equations:
9x4y = 28
9(28/5)(-14/5) = 28
-352/25 = 28/25 (true)
2x + 4y = 0
2(28/5) + 4(-14/5) = 0
56/5 - 56/5 = 0 (true)
Therefore, the solution is verified.
2. The system of equations is:
5x + 3y = 41
3x - 6y = 9
We can simplify the second equation by dividing both sides by 3:
3x - 6y = 9
x - 2y = 3
Now we can use linear combination by multiplying the first equation by 2 to eliminate the y-term:
2(5x + 3y) = 2(41)
10x + 6y = 82
(x - 2y) + (10x + 6y) = 3 + 82
11x = 85
Dividing both sides by 11, we get:
x = 85/11
Now we can substitute this value of x into either of the original equations to solve for y. Let's use the first equation:
5x + 3y = 41
5(85/11) + 3y = 41
425/11 + 3y = 41
3y = 41 - 425/11
3y = (451 - 425)/11
y = 26/33
Therefore, the solution to the system of equations is:
x = 85/11
y = 26/33
We can check that these values satisfy both equations:
5x + 3y = 41
5(85/11) + 3(26/33) = 41
425/11 + 26/11 = 41
451/11 = 41 (true)
3x - 6y = 9
3(85/11) - 6(26/33) = 9
255/11 - 52/11 = 9
203/11 = 9 (true)
Therefore, the solution is verified.
3.
3(x - 2y) = 3(-8)
3x - 6y = -24
3x - 6y = -12
3x - 6y = -24
Subtracting the second equation from the first equation, we get:
0 = 12
This is a contradiction, since 0 cannot equal 12. Therefore, there is no solution that satisfies both equations.
This means that the system is inconsistent, and there are no solutions.
Read more on linear combination here: https://brainly.com/question/14495533
#SPJ1
if the correlation between the response variable and the explanatory variables is sufficiently low, then adjusted r^2 may be
Answers
If the correlation between the response variable and the explanatory variables is sufficiently low, the adjusted R-squared may be close to or lower than zero.
Adjusted R-squared is a statistical measure that assesses the goodness of fit of a regression model. It adjusts the R-squared value to account for the number of predictors (explanatory variables) in the model.
Adjusted R-squared takes into consideration the sample size and the complexity of the model, penalizing the inclusion of unnecessary predictors.
R-squared represents the proportion of the variance in the response variable that can be explained by the predictors. It ranges from 0 to 1, with higher values indicating a better fit. However, R-squared can be inflated by including irrelevant or weak predictors in the model.
When the correlation between the response variable and the explanatory variables is low, it suggests that the predictors are not strongly related to the response variable.
In this case, the model may not provide a good fit to the data, and the R-squared value may be low. Adjusted R-squared takes into account the low correlation and the number of predictors, and it can be close to or even lower than zero.
A low or negative adjusted R-squared indicates that the model does not explain much of the variation in the response variable and may not be useful for making predictions or drawing conclusions.
It suggests that there may be other factors or variables that are more relevant in explaining the variation in the response variable.
To know more about variable click here
brainly.com/question/2466865
#SPJ11
John and Mary had Php 384 altogether. After John gave Php 36 to Mary, Mary had 3 times as much money as John. How much money did Mary had at first?
Answers
John initially had Php 132 and Mary initially had Php 252 (384 - 132).
Let's start by setting up the equations to solve for this problem.
Let x be the amount of money John had initially.
Then, Mary had (384 - x) initially.
After John gave Php 36 to Mary, John had (x - 36) left and Mary had (384 - x + 36) = (420 - x).
We are told that Mary had three times as much money as John after this transaction, so we can write:
3(x - 36) = 420 - x
Simplifying this equation gives:
3x - 108 = 420 - x
4x = 528
x = 132
Therefore, John initially had Php 132 and Mary initially had Php 252 (384 - 132).
Answer: Mary had Php 252 at first.
Learn more about initially from
https://brainly.com/question/31041139
#SPJ11
H.C.F of 378 and 567 and 252
Answers
Answer:
Their highest common factor is the number 9
See photo for question

Answers
Answer:
66 = ∠JKN
Step-by-step explanation:
∠JKM = 99
∠LKM = 66
KN bisects means middle point divides into two equal parts
so first lets find ∠LKN and ∠NKM
66/2 = ∠LKN and ∠NKM each
33 = ∠LKN
33 = ∠NKM
so if we add ∠JKL + ∠LKN + ∠NKM = 99
∠JKL + ∠LKN + ∠NKM = 99
∠JKL + 33 + 33 = 99
∠JKL + 66 = 99
∠JKL = 99-66
∠JKL = 33
now to find ∠JKN we must add
∠JKL + ∠LKN = ∠JKN
33 + 33 = ∠JKN
66 = ∠JKN
Noelle is making a rectangular place mat that is 15 inches wide and 18 inches long. What is the least amount of fabric that she will need to make the place mat?
Answers
Answer:
270 in
Step-by-step explanation:
the least amount of fabric she would need is equal to the area of the mat
the mat is in the shape of a rectangle
Area of a rectangle = length x width
15 x 18 = 270 in²
1. How many significant figures are in each of the following measurement? a. \( 143 \mathrm{~g} \) b. 0.074-meter c. \( 8.750 \times 10^{-2} \mathrm{~g} \) d. \( 1.072 \) meter 2. In which of the foll"
Answers
1. Determining the number of significant figures in given measurements:
a. 143 g - It contains three significant figures since each digit is measured and identified by the observer.
b. 0.074-meter - It contains two significant figures since 0 before the first non-zero digit (7) doesn't add any value.
c. 8.750 × 10−2 g - It contains four significant figures since all the non-zero digits are significant.
Also, the scientific notation indicates that the zeros on the left side are not significant.d. 1.072 meter - It contains four significant figures since each digit represents a measured value and is essential.
2. Out of the following values, - kg, s, m, or kmSolution:In the given options, kg represents the unit of mass, s represents the unit of time, m represents the unit of length, and km represents the unit of length (kilometer).Therefore, kg is not a unit of length.
To know more about measurements visit:
https://brainly.com/question/28913275
#SPJ11
Which is the table that shows the multiplication of x2 - 4x + 4 and 6x + 3?
Ο Α.
6x
3
x2
6x3
3x2
--4x
-24x2
-12x
4
24x
12
B.
6x
3
x²
6x2
3x2
-4x
-24x
-12x
4
24x
12
O
C.
X2
6x
3
6х3
-4x
-24x2
-72x2
4
24x
72x
18x3
Answers
Hey I’m having a lot of trouble solving this and I was wondering if you can help

Answers
Angle DGO: Vertical ->13 (no letter), supplement PGD marked as L
Angle 12: Vertical-> HOG marked as K
Angle 2: Vertical -> ICK (not in table). Supplement #15, letter E
Angle 28: Vertical #8, letter E
Angle 31: Vertical #19, letter W
Angle GRV: Supplement #19, letter E
Angle 21: Supplement #7, letter I
Angle 22: Vertical #17, letter H
Angle 32: Supplement #17, letter T
Checking previous answers.....
Angle 4: Vertical ORY, letter H. Correct
Angle RKV: Supplement VKA, letter E. Correct
Angle 26: Vertical #7, letter D. Correct
Angle 24: Supplement #8, letter I. Correct
Angle 26: Vertical #7, letter D. Correct
Angle 18: Vertical VKA, letter N. Correct
Angle 29: Supplement HOG, letter T. Correct
Angle YRV: Supplement ORY, letter I. Check!!
Angle 27: Vertical #15, letter T. Correct
Angle 4 (already checked).
Angle EGJ: Vertical PGD, letter G. Correct
help me!! will give brainly helppppp

Answers
Answer:
SJSGGSHB AAJAM SLE AS THE MONSY UWY WHY AH AI
mrs hough is building a raised garden next to her 13.5 ft fence so she only needs fencing to go around the other 3 sides. if the area of the garden is 121.5 sw ft how much fencing does she need
Answers
Mrs. Hough would need 31.5 feet of fencing for the other three sides of the garden.
To calculate the amount of fencing needed for Mrs. Hough's raised garden, we first need to determine the dimensions of the garden.
Since the garden is next to a 13.5 ft fence, we know that one side of the garden is 13.5 ft.
Let's assume the other two sides of the garden have lengths x and y.
The area of the garden is given as 121.5 sq ft, so we have the equation:
x × y = 121.5
To find the dimensions of the garden, we can solve this equation. One possible solution is x = 9 ft and y = 13.5 ft.
Therefore, the dimensions of the garden are 9 ft by 13.5 ft.
Now, to calculate the amount of fencing needed, we add up the lengths of the three sides (excluding the side next to the fence):
Fencing needed = x + y + x = 9 ft + 13.5 ft + 9 ft = 31.5 ft
Mrs. Hough would need 31.5 feet of fencing for the other three sides of the garden.
To know more about Equation related question visit:
https://brainly.com/question/29657983
#SPJ11
The given point 1, -3 reflected over the x axis
Answers
Answer:
(1,3)
Step-by-step explanation:
The image of (1, -3) is (1, 3).
What is a reflection?There are two ways of reflection.
Along x-axis:
(x, y) – (x, -y)
Along y-axis:
(x, y) - (-x, y)
We have,
Point = (1. -3)
Reflected over the x-axis.
So,
(1, -3) = (1, -(-3)) = (1, 3)
Thus,
(1, 3) is the reflected image.
Learn more about reflections here:
https://brainly.com/question/12463306
#SPJ2
Use Gaussian elimination to find the complete solution to the system of equations, or show that none exists.w−4x−y−5z=−21w+x−y=−15w+5x+z=23x−2y+z=6
Answers
Using Gaussian elimination, the complete solution to the system of equations is (w, x, y, z) = (-8/19, 54/95, 39/19, 0).
To solve the system of equations using Gaussian elimination, we first write the augmented matrix:
\(\begin{bmatrix}1 & -4 & -1 & | & -5 \\0 & 5 & -2 & | & 5 \\0 & 9 & 1 & | & 6 \\0 & 1 & -2 & | & 1 \\\end{bmatrix}$$\)
Next, we perform row operations to reduce the matrix to row echelon form:
R2 = R2 - R1:
\(\begin{bmatrix} 1 & -4 & -1 & -5 & \big| & -21 \\ 0 & 5 & -2 & 5 & \big| & 6 \\ 1 & 5 & 0 & 1 & \big| & 23 \\ 0 & 1 & -2 & 1 & \big| & 6 \end{bmatrix}\)
R3 = R3 - R1:
\(\begin{bmatrix}1 & -4 & -1 & -5 & | & -21 \\0 & 5 & -2 & 5 & | & 6 \\0 & 9 & 1 & 6 & | & 44 \\0 & 1 & -2 & 1 & | & 6 \\\end{bmatrix}\)
R3 = R3 - 9R2:
\(\begin{bmatrix}1 & -4 & -1 & -5 & | & -21 \\0 & 5 & -2 & 5 & | & 6 \\0 & 0 & 19 & -39 & | & -14 \\0 & 1 & -2 & 1 & | & 6\end{bmatrix}\)
R4 = R4 - R2:
\(\begin{bmatrix}1 & -4 & -1 & -5 \\0 & 5 & -2 & 5 \\0 & 0 & 19 & -39 \\0 & 0 & 0 & -4\end{bmatrix}\)
Now we have the row echelon form of the augmented matrix, and we can solve for the variables using back substitution. From the last row, we have -4z = 0, so z = 0.
Substituting this into the third row, we get 19y = 39, or y = 39/19. Substituting these values into the second row, we get 5x - 10(39/19) = 6, or x = 54/95. Finally, substituting all three values into the first row, we get w = -8/19.
Learn more about Gaussian elimination at
https://brainly.com/question/31328117
#SPJ4
find the equation of the line that passes trougth the points (6, 3), (9, 15) in slope intercept form
Answers
Explanation
Step 1
find the slope
the slope is given by:
\(\begin{gathered} \text{slope}=\frac{y_2-y_1}{x_2-x_1} \\ \text{where} \\ P1(x_1,y_1) \\ P2(x_2,y_2) \end{gathered}\)Let
P1(6,3)
P2(9,15)
replacing.
\(\begin{gathered} \text{slope}=\frac{y_2-y_1}{x_2-x_1} \\ \text{slope}=\frac{15-3}{9-6}=\frac{12}{3}=4 \\ \text{slope}=4 \end{gathered}\)Step 2
using
slope=4
P1(6,3)
find the equation
\(\begin{gathered} y-y_1=m(x-x_1) \\ \text{replacing} \\ y-3=4(x-6) \\ y-3=4x-24 \\ \text{add 3 in both sides} \\ y-3+3=4x-24+3 \\ y=4x-21 \end{gathered}\)I hope this helps you
find the sum of the first 9 terms of the following series, to the nearest integer. 75 , 60 , 48 , . . . 75,60,48,...
Answers
The sum of the first 9 terms of the geometric sequence 75, 60, 48 is given as follows:
325.
What is a geometric sequence?A geometric sequence is a sequence of numbers where each term is obtained by multiplying the previous term by a fixed number called the common ratio q.
The formula for the sum of the first n terms is given as follows:
\(S_n = a_1\frac{q^n - 1}{q - 1}\)
In which \(a_1\) is the first term.
The parameters for this problem are given as follows:
\(a_1 = 75, q = 0.8, n = 9\)
Hence the sum is given as follows:
\(S_9 = 75 \times \frac{0.8^9 - 1}{0.8 - 1}\)
\(S_9 = 325\)
More can be learned about geometric sequences at https://brainly.com/question/24643676
#SPJ1
The number of ways to arrange x successes among n trials is equal to?
Answers
The number of ways to arrange x successes among n trials is equal to ( n! ) / ( x! ( n - x )! ) .
We need o find the number of ways to arrange x successes among n trials. And to find the number of ways to arrange x successes among n trials we will use the formula mentioned below;
( n! ) / ( x! ( n - x )! )
Here, to find the value of n! and x! we can use the formula mentioned below;
n! = n × ( n -1 ) × ( n - 2 ).............. ×1
x! = x (x - 1) ( x - 2 ).............×1
Thus, we can conclude that ( n! ) / ( x! ( n - x )! ) represents the number of ways to arrange x successes among n trials.
To know more about Factorial refer to the link:
https://brainly.com/question/25997932
#SPJ4
If f(x) is a third degree polynomial function, how many distinct complex roots are possible?
0 or 2
0, 1, 2, or 3
1 or 2
1, 2, or 3
Answers
Answer:
first onei think
Step-by-step explanation: I think sorry if im wrong
Q; If f(x) is a third degree polynomial function, how many distinct complex roots are possible?
A; 0 or 2
determine whether the series converges or diverges. [infinity] 5^n 1 4n − 2 n = 1
Answers
To determine whether the series converges or diverges, we need to analyze the given series. The series is:
Σ (5^n / (4n - 2)), from n = 1 to infinity.
To check for convergence, we can apply the Ratio Test, which involves finding the limit of the ratio between consecutive terms. Let's denote the term a_n as (5^n / (4n - 2)). Then, we'll compute the limit as n approaches infinity:
lim (n→∞) (a_(n+1) / a_n) = lim (n→∞) ((5^(n+1) / (4(n+1) - 2)) / (5^n / (4n - 2)))
Simplifying this expression, we get:
lim (n→∞) (5^(n+1) / 5^n) * ((4n - 2) / (4(n+1) - 2))
The first part of the limit simplifies to:
lim (n→∞) 5 = 5
The second part of the limit becomes:
lim (n→∞) ((4n - 2) / (4n + 2)) = 1
Multiplying both limits, we get:
5 * 1 = 5
Since the limit is greater than 1, the Ratio Test indicates that the series diverges.
Learn more about Ratio Test: https://brainly.com/question/29579790
#SPJ11
At what point does the health insurance company cover all of the out-of-pocket costs for an
insured individual on the economy plan?
a. Above $1,200 in-network or $2,400 out-of-network
b. Above $3,300 in-network or $6,000 out-of-network
Above $7,000 in-network or $12,000 out-of-network
d. Above $14,000 in-network or $24,000 out-of-network
C.
Answers
The point at which the health insurance company cover all of the out-of-pocket costs for an insured individual on the economy plan is; Option C
What is Out of Pocket Expenses?
Out-of-pocket expenses is defined as the costs that individuals pay out of their own cash reserves. In terms of health insurance, out-of-pocket expenses are simply your own share of covered healthcare costs, including the money you pay for deductibles, copays, and coinsurance.
Now, in the year 2021, the out-of-pocket limits were $8,550 for individual coverage and $17,100 for family. However, now in the year 2022, the out-of-pocket limits for individuals is now $8,700 while it is now $17,400 for a family.
Thus, we can conclude that option C is correct from the range given.
Read more about Insurance at; https://brainly.com/question/4953989
i really need help..im confused

Answers
The marginal frequencies of chocolate and strawberry are 0.75 and 0.25 and chocolate is greater by 0.5
What are marginal frequencies?Marginal frequency is the ratio between either a column total or a row total and the total sample size.
For example, in a table of students classified by sex and area of study, the number of female students, regardless of area of study, would be one marginal frequency.
The marginal frequency of chocolate is calculated as;
The total frequency of chocolate = 30+45 = 75
The grand frequency = 75+25 = 100
marginal frequency of chocolate = 75/100
= 0.75
The marginal frequency of strawberry = 25/100
= 0.25
The difference in the marginal frequencies of chocolate and strawberry = 0.75 - 0.25 = 0.50
Therefore the marginal frequency of chocolate is greater than strawberry by 0.5
learn more about marginal frequency from
https://brainly.com/question/27506923
#SPJ1
Determine if the sequence below is arithmetic or geometric and determine the
common difference / ratio in simplest form.
4, 2, 1, ...
Answers
Answer:
This is a geometric sequence, and the common difference/ratio is 0.5
Step-by-step explanation:
The difference between 4 and 2 is * 0.5, or 1/2, which is the same between 2 and 1. This means that we are dividing.
Remember that arithmetic means plus or minus, while geometric means multiplication or division. Because we are dividing, this is a geometric sequence.
The common difference/ratio in this is divided by 2, which is the same as being multiplied by 0.5.
22. A sandpitJis designed in the shape of a trapezium, with the dimensions shown.
If the area of the sandpit is 14 m², what will be its perimeter
Answers
Answer:
hey here is ur answer
the perimeter of a square = 4* side
4*s=14
S = 14/4
s= 7/2 or 3.5
area = side * side
area = (7/2) sq
area = 12.25sq m
Step-by-step explanation:
write the general expression of the continuity equation and its particular expression if fluid incompressibility is assumed.
Answers
The continuity equation is a fundamental principle in fluid dynamics that expresses the conservation of mass for a fluid. It states that the rate of change of mass in a fluid is equal to the net flow of mass into or out of a given volume. Mathematically, the general expression of the continuity equation is:
∂ρ/∂t + ∇ · (ρv) = 0
where ρ is the fluid density, t is time, v is the fluid velocity, and ∇ · is the divergence operator.
If the fluid is assumed to be incompressible, which means that the density remains constant throughout the flow, the continuity equation simplifies to:
∇ · v = 0
This equation states that the divergence of the velocity field is zero, which implies that the volume flow rate is conserved along any path in the fluid. In other words, if the fluid is incompressible, the rate at which fluid flows into a given volume must be equal to the rate at which it flows out of that volume. The continuity equation is a powerful tool in fluid mechanics that helps to describe the behavior of fluids in a wide range of applications, from weather forecasting to the design of aircraft and ships.
Learn more about fluid dynamics here:
https://brainly.com/question/30578986
#SPJ11