Which of the following equations are equivalent? Select three options. 2 + x = 5 x + 1 = 4 9 + x = 6 x + (negative 4) = 7 Negative 5 + x = negative 2
Answers
Related Questions
Find the missing angle.
200
180
A
100
B
50
SO
D) 70

Answers
Answer:
the answer is c) 80
all angles of the Triangle will have a sum of 180. 80+20=100 ... 180-100= 80
Will give brainliest answer


Answers
Answer:
B
Step-by-step explanation:
y = - |x-4|+8 ... f(x)
==> y= -|x-1|+3 ... y = f(x+3) - 5 .. horizontal translate left 3 units and
vertical translate down 5 units

PLEASE HELP DUE SOON! PLEASE SHOW WORK SO I KNOW HOW TO IT FOR NEXT TIME! IM STUCK ON THIS AND ITS DUE TODAY!!!!! YOU WILL GETT 100 POINTS REAL ANSWERS ONLY! MANY THANKS! QUESTIONS DOWN BELOW!!!!!

Answers
Answer:
a) zero triangles.
b) one triangle.
Step-by-step explanation:
In triangle ABC:
A, B and C are the interior angles.a, b and c are the sides opposite the corresponding interior angles.Part (a)Given:
∠A = 51°a = 10 cmb = 28 cmLaw of Sines
\(\sf \dfrac{\sin A}{a}=\dfrac{\sin B}{b}=\dfrac{\sin C}{c}\)
(where A, B and C are the angles and a, b and c are the sides opposite the angles)
To determine if any triangles are possible, substitute the given values into the Law of Sines to find angle B:
\(\implies \sf \dfrac{\sin 51^{\circ}}{10}=\dfrac{\sin B}{28}\)
\(\implies \sf \sin B=\dfrac{28\sin 51^{\circ}}{10}\)
\(\implies \sf \sin B=2.176008...\)
As -1 ≤ sin B ≤ 1, there is no solution for angle B.
Therefore, zero triangles are possible.
----------------------------------------------------------------------------------
Part (b)Given:
∠C = 30°a = 24 cmc = 12 cmLaw of Sines
\(\sf \dfrac{\sin A}{a}=\dfrac{\sin B}{b}=\dfrac{\sin C}{c}\)
(where A, B and C are the angles and a, b and c are the sides opposite the angles)
To determine if any triangles are possible, substitute the given values into the Law of Sines to find angle A:
\(\implies \sf \dfrac{\sin A}{24}=\dfrac{\sin 30^{\circ}}{12}\)
\(\implies \sf \sin A=\dfrac{24\sin 30^{\circ}}{12}\)
\(\implies \sf \sin A=1\)
\(\implies \sf A=\sin^{-1}(1)\)
\(\implies \sf A=90^{\circ}\)
Therefore, one triangle is possible (see attachment).

Will mark as brainlist answer quickly
The Vikings considered speed an important quality in a ship. What evidence
from the passage supports this conclusion?
A: The hulls of the drekar were shallow and fat so the ships rode high in the
water.
B: The drekar had very large sails and space for many oarsmen.
C: The drekar were light enough to be carried from one body of water to
another.
D: The drekar could be driven right onto beaches to allow soldiers to jump
over the side.
Answers
Answer:
A. The hulls of the drekar were shallow and fat so the ships rode high in the water.
Step-by-step explanation:
Hope this helps :)
Use the graph to find f(3).
f(3)=

Answers
Answer:
f(3) = -2
General Formulas and Concepts:
Algebra I
Reading a Cartesian Graph Function NotationStep-by-step explanation:
f(3) is simply asking for the y-value when x = 3. According to the graph, when x = 3, y = -2.
Therefore, f(3) = -2
The point P=(1/2,y)lies on the unit circle shown below. What is the value of y in simplest form?
Answers
The value of y in simplest form for the point P = (1/2, y) lying on the unit circle is y = ± √(3)/2.
To find the value of y in simplest form for the point P = (1/2, y) lying on the unit circle, we can use the equation of the unit circle, which states that for any point (x, y) on the unit circle, the following equation holds: x^2 + y^2 = 1.
Plugging in the coordinates of the point P = (1/2, y), we get:
(1/2)^2 + y^2 = 1
1/4 + y^2 = 1
y^2 = 1 - 1/4
y^2 = 3/4.
To simplify y^2 = 3/4, we take the square root of both sides:y = ± √(3/4).
Now, we need to simplify √(3/4). Since 3 and 4 share a common factor of 1, we can simplify further: y = ± √(3/4) = ± √(3)/√(4) = ± √(3)/2.
for more search question point
https://brainly.com/question/28162977
#SPJ8
when creating a scatterplot, always put the categorical variable on the vertical axis. always put the categorical variable on the horizontal axis. if you have an explanatory variable, put it on the horizontal axis. if you have a response variable, put it on the horizontal axis.
Answers
When creating a scatterplot, it is important to carefully consider which variable to place on the vertical and horizontal axes.
The vertical axis is commonly used to represent the response or dependent variable, while the horizontal axis is used for the explanatory or independent variable.
However, when dealing with a categorical variable, there is no inherent order or numerical relationship between the categories. Thus, it does not make sense to use either axis as a response or explanatory variable. In this case, the categorical variable should be placed on either axis based on what makes the most sense for the data being displayed.
If there is an explanatory variable and a response variable, the explanatory variable should be placed on the horizontal axis and the response variable on the vertical axis. This is because the explanatory variable is usually the variable that is being manipulated or controlled, while the response variable is the one that is being measured or observed.
Overall, the placement of variables on the axes of a scatterplot should be based on the nature of the data being displayed and the relationship between the variables being studied.
To know more about a scatterplot click here:
brainly.com/question/30017616
#SPJ4
Help, this is my math hw and I don't get it!
Pictures are attached below...
I need to show my work too, so i need a file to your work!
I'll mark brainliest if you can answer it.


Answers
So 3x KLM = 72 deg.
KLM = 72 / 3 = 24 deg
MLN = 2x KLM = 24 x 2 = 48 deg.
x+2y-z=5
-X-y+2z=-13
2x+y-2z=14
Answers
Answer:
\(x+2y-z=5 ...(1)\\ -x-y+2z=-13...(2) \\ 2x+y-2z=14...(3) \\ \\ add \: (2) + (3) \\\boxed{x= 1} \\ 2 \times (1) + (2) \\ x + 3y = - 3 \\ 1 + 3y = - 3 \\ 3y = - 4 \\ \boxed{y = - \frac{4}{3} }\\ solve \: for \: z \\ x + 2y - z = 5 \\ 1-\frac{4}{3}(2)-z=5\\3-8-3z=15\\3z=-20\\\boxed{z = - \frac{20}{3} }\)
Help me with this worksheet pls

Answers
The value of y from x= 0 to x = 3 is: y = 5(2)⁰ = 5, y = 5(2)¹ = 10, y = 5(2)² = 20, y = 5(2)³ = 40. The most rapid rate of change is: y = 7ˣ. The constant 1.20 is greater than 1 thus, the function is exponential growth.
What is exponential function?The formula for an exponential function is f (x) = axe, where x is a variable and an is a constant that serves as the function's base and must be bigger than 0. The transcendental number e, or roughly 2.71828, is the most often used exponential function basis.
The given function is:
y = 5(2)ˣ
The value of y from x= 0 to x = 3 is:
y = 5(2)⁰ = 5
y = 5(2)¹ = 10
y = 5(2)² = 20
y = 5(2)³ = 40
The most rapid rate of change as x increases beyond 0 is:
y = 7ˣ
This is observed as the graph increases rapidly with change in value of x.
3. y = (1.20)ˣ
The constant 1.20 is greater than 1 thus, the function is exponential growth.
Learn more about exponential function here:
https://brainly.com/question/15352175
#SPJ1
Three solid shapes, A B and C are similar. The surface area of shape A is 9cm² The surface area of shape B is 16cm² The ratio of the volume of shape B to shape C is 27:125 Work out the ratio of the height of shape A to shape B Give your answer in its simplest form.
Answers
Answer:
9:20
Step-by-step explanation:
The ratio of the surface area of similar solid is equal to the square of the ratio of their corresponding linear measures.
If the ratio of their corresponding linear measures is a:b, the surface area ratio will be (a/b)².
Therefore, (A/B )² = 9/16
square root both sides A/B = √9/√16 A/B = 3/4 A:B = 3:4
The ratio of volume of two similar solid is the ratio cube of their corresponding linear measures.
Therefore, (B/C)³ = 27/125 cube root both sides B/C = 3/5 B:C = 3:5
To make the ratio equivalent A:B:C = 9:12:20
A:C = 9:20
What polygon has an interior angle sum of 1260?; What is the measure of one interior angle of a polygon?; What is the sum of the measure of the interior angles of a regular polygon?; What is the sum of the measures of the interior angles of a regular polygon of six sides?
Answers
The polygon is a decagon, measure of one interior angle is equal to the sum of the interior angles divided by the number of sides and measure of an interior angle is (n - 2) * 180 and the toal measures of the interior angles polygon of six sides are 1080.
A polygon is a closed two-dimensional shape composed of straight line segments. The sides of a polygon are joined together to form a single shape. Polygons can be categorized into different types, such as triangles, quadrilaterals, pentagons, hexagons, and octagons. A decagon is a 10-sided polygon. It is a two-dimensional figure with ten edges and ten vertices. It is a type of polygon that has interior angles that add up to 1440 degrees. It is a regular polygon, meaning all of its sides are of equal length and its angles are equal. It is often used in architecture, design, and engineering for decoration and structural purposes. Decagons can also be found in nature, such as in some snowflakes and in the seeds of some flowers. Decagons are versatile shapes that have numerous applications and are a popular choice for both decorative and practical reasons.
To know more about polygons refer to the link brainly.com/question/24464711
#SPJ4
Maeve takes pictures of people as they enter an amusement park. She makes $40 per day, plus $4 for each person who buys a picture. If Maeve made $80 yesterday, how many people bought a picture?
Answers
Answer:
20People
Step-by-step explanation:
Buying of a picture = $4
if the total revenue made after people bought it was $80
Total number of people who bought it
= $80/$4
=20People
Solve each system of linear equations below, then check your work.
A. 3x−y=−11 −x+y=5
B -2y+3= 4x + 2 6x + 4y=1
C. 32y- x= -25 5x= 100 + x - 8Y
D. 2y + 3x = 6 4x + 5y +20 = 0
Answers
A. The solution of linear equation is (x, y) = (-3, 8).
B. The solution is (x, y) = (3/4, -1).
C. The solution is (x, y) = (-31/8, 3/8).
D. The solution is (x, y) = (55/7, -117/14).
A. 3x - y = -11 --- (1)
-x + y = 5 --- (2)
From equation (2), we can write y = x + 5, and substitute it in equation (1):
3x - (x + 5) = -11
2x = -6
x = -3
Substituting x in equation (2):
-y = -8
y = 8
Therefore, the solution of the system is (x, y) = (-3, 8).
To check the solution, we substitute the values of x and y in the original equations:
3(-3) - 8 = -11 (True)
-(-3) + 8 = 5 (True)
So, the solution is correct.
B. -2y + 3 = 4x + 2 --- (1)
6x + 4y = 1 --- (2)
From equation (1), we can write 4x + 2 = -2y + 3, and substitute it in equation (2):
6x + 4y = 1
6x - 4y = 8 (rearranging)
12x = 9
x = 3/4
Substituting x in equation (1):
-2y + 3 = 4(3/4) + 2
-2y + 3 = 5
-2y = 2
y = -1
Therefore, the solution of the system is (x, y) = (3/4, -1).
To check the solution, we substitute the values of x and y in the original equations:
-2(-1) + 3 = 4(3/4) + 2 (True)
6(3/4) + 4(-1) = 1 (True)
So, the solution is correct.
C. 32y - x = -25 --- (1)
5x = 100 + x - 8y --- (2)
From equation (2), we can write 4x = 100 - 8y, and substitute it in equation (1):
32y - x = -25
32y - (100 - 8y) = -25
40y = 75
y = 3/8
Substituting y in equation (1):
32(3/8) - x = -25
x = -31/8.
Therefore, the solution of the system is (x, y) = (-31/8, 3/8).
To check the solution, we substitute the values of x and y in the original equations:
32(3/8) - (-31/8) = -25 (True)
5(-31/8) = 100 + (-31/8) - 8(3/8) (True)
So, the solution is correct.
D. To solve the system of equations:
2y + 3x = 6 --- (1)
4x + 5y + 20 = 0 --- (2)
We can rearrange equation (2) to isolate one of the variables:
4x + 5y = -20 (subtracting 20 from both sides)
5y = -4x - 20 (subtracting 4x from both sides)
y = (-4/5)x - 4 (dividing both sides by 5)
Substituting this value of y in equation (1):
2((-4/5)x - 4) + 3x = 6
(-8/5)x - 8 + 3x = 6
(-8/5)x + 3x = 14
(-8/5 + 3)x = 14
(-8/5 + 15/5)x = 14
(7/5)x = 14
x = 10
Substituting this value of x in the equation for y:
y = (-4/5)(10) - 4
y = -12.
Therefore, the solution of the system is (x, y) = (10, -12).
To check the solution, we substitute the values of x and y in the original equations:
2(-12) + 3(10) = 6 (True)
4(10) + 5(-12) + 20 = 0 (True)
So, the solution is correct.
For similar question on linear equations.
https://brainly.com/question/2030026
#SPJ11
lect the correct answer.
Under which condition is the sample proportion, , a point estimate of the population proportion?
A.
The sample proportion is never a point estimate of the population proportion.
B.
The sample represents a proportion of the population.
C.
The sample proportion is unbiased.
D.
The sample size, n, is small enough.
Reset Next
Answers
The correct answer is B. The sample represents a proportion of the population.
What is the sample population ?
A point estimate is a single value used to estimate a population's unknown parameter. The sample proportion (denoted by p), in the context of determining the population proportion, is a widely used point estimate. The sample proportion is determined by dividing the sample's success rate by the sample size.
The sample must be representative of the population for it to be a reliable point estimate of the population proportion. To accurately reflect the proportions of various groups or categories present in the population, the sample should be chosen at random.
Learn more about population:https://brainly.com/question/30324262
#SPJ1
2) The mass of a radioactive element decays at rate given by m(t) = m0e^-rt, where m(t) is the mass at any time t, m0 is the initial mass, and r is the rate of decay.Uranium-240 has a rate of decay of .0491593745. What is the mass of U-240 left after 10 hours, if the initial mass is 50 grams? (Use e = 2.71828.]A) 28.54387 gB) 30.58254 gC) 32.14286 gD) 32.68034 g
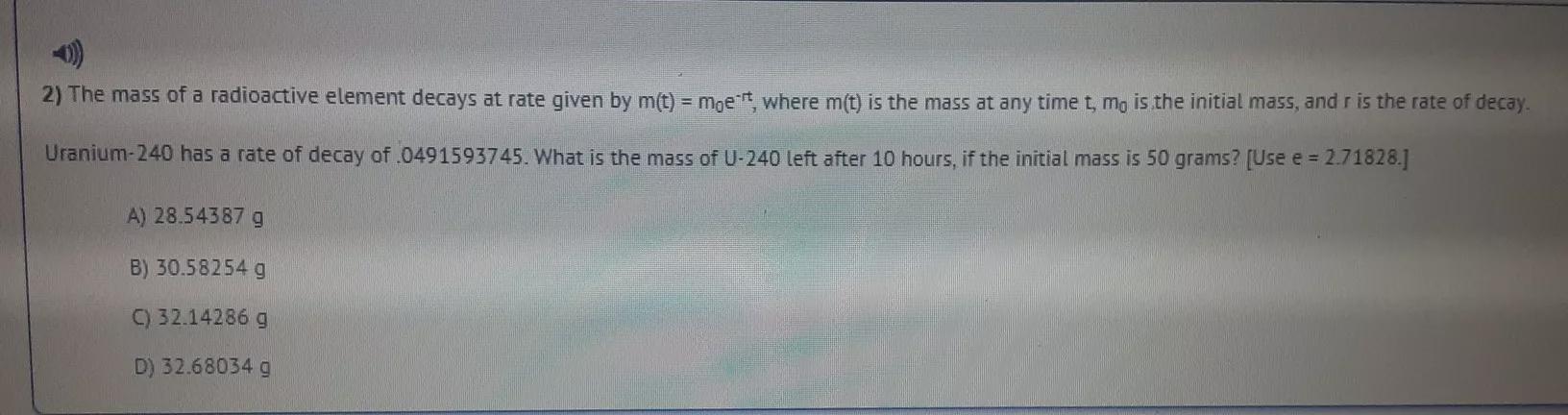
Answers
Solution
- We are given the following formula:
\(\begin{gathered} m(t)=m_0e^{-rt} \\ \text{where,} \\ r=\text{decay rate} \\ t=\text{time} \\ m_0=\text{ Initial mass} \\ m=\text{mass after time t} \end{gathered}\)- We are told that the Initial mass is 50g, the decay rate is .0491593745, time (t) is 10 hours, and e = 2.71828.
- With the above information, we can proceed to substitute the values given into the formula and get the mass of Uranium after 10 hours.
- This is done below:
\(\begin{gathered} m=50\times2.71828^{-(0.0491593745)\times10} \\ \\ m=50\times0.611651003817 \\ \\ \therefore m=30.5825\ldots\approx30.58254g \end{gathered}\)Final Answer
The answer is 30.58254g (OPTION B)
ANSWER IT PLZZZZZZZZZZZZZ

Answers
Answer:
the answer is 2 :)
have a good day !!
Step-by-step explanation:
16/4(2)
16/8
=2
Which sample described below will most accurately describe the population?
A. A sample of 12 former politicians about their thoughts on gun control.
B. A sample of 500 adults who are asked their opinion about a recent law enacted.
Answers
Answer:
B. A sample of 500 adults who are asked their opinion about a recent law enacted.
Step-by-step explanation:
The population would be more accurately described by 500 regular people than politicians
If 75% of a number is 255 and 20% of the same number is 68, find 95% of that
number.
Answers
Answer:
75% may also be expressed as 75/100=3/4 or as 0.75 as needed.
Let x = the number
Translate:
"if 75% of a number is 60" means
(75/100) * x = 60 [the word "of" usually means multiply]
(3/4) x = 60 [reduce or just write it this way]
x = 60(4/3) [multiply both sides by 4/3]
x = 80
Step-by-step explanation:
find the value of x to the nearest tenth

Answers
Answer:
x = 41.2
Step-by-step explanation:
Assuming the dotted line at the top is parallel to the segment with length x, it follows from the alternate interior angles theorem that the interior angle of the triangle (marked in diagram) is also 27º.
Using SOH-CAH-TOA, we get that tan(27º) = 21/x, so x = 21/tan(27º), which is approximately equal to 41.2.

pls help! a small box measures 5in. by 10 in. By 7 in height. Find the volume of the box
Answers
Answer:
350
Step-by-step explanation:
Verify that the function \(g(x)=2x^3-3x+1\) satisfies the three hypotheses of Rolle’s Theorem on the interval \([0,2]\).
Answers
Answer:
the funtion does not satisfies the hypothese f(a)=f(b), just because when evaluate f(0) = 1 and when evaluate f(2) = 11,
26.) A line has a slope of .What is the slope of any line parallel to this line?F-!GH

Answers
Given data:
The given slope of the line is m=3/7.
The slope of the line parallel to the given line is,
m'=m
m'=3/7
Thus, option H) is correct.
HELP PLEASE!!
Quadrilateral CDEF is a rhombus. What is m

Answers
Answer:
∠ BDC = 29°
Step-by-step explanation:
the sides of a rhombus are congruent, so CD = ED and Δ EDC is therefore isosceles with base angles congruent , then
∠ BCD = ∠ BED = 61°
• the diagonals are perpendicular bisectors of each other , then
∠ CBD = 90°
the sum of the 3 angles in Δ BCD = 180°
∠ BDC + ∠ CBD + ∠ BCD = 180°
∠ BDC + 90° + 61° = 180°
∠ BDC + 151° = 180° ( subtract 151° from both sides )
∠ BDC = 29°
what is a decimal in mathematics
Answers
Answer:
a decimal number can be defined as a number whose whole number part and the fractional part is separated by a decimal point. The dot in a decimal number is called a decimal point. The digits following the decimal point show a value smaller than one.
Step-by-step explanation:
The home states of a certain group of people are distributed as follows: 52 percent are from MISSOURI, 28 percent are from KANSAS, and 20 percent are from IOWA. (No one in the group had a home state other than one of these three.) (Note: Your answer to the question below should be rounded to three decimal places.) Suppose we randomly select a person from this group. What is the expected value of the number of letters in the selected person's home state
Answers
Answer:
The expected value of the number of letters in the selected person's home state is 6.64.
Step-by-step explanation:
What is the expected value of the number of letters in the selected person's home state
52% have 8 letters(Missouri).
28% have 6 letters(Kansas)
20% have 4 letters(Iowa).
So
\(E = 0.52*8 + 0.28*6 + 0.2*4 = 6.64\)
The expected value of the number of letters in the selected person's home state is 6.64.
The expected value of the number of letters in the selected person's home state will be 6.64.
52% are from MISSOURI of 8 letters.
28% are from KANSAS of 6 letters.
20% are from IOWA of 4 letters.
The expected value of the number of letters in the selected person's home state is required.
Let's consider the expected value E
So, 52% of 8 + 28% of 6 + 20% of 4 = E
\(\rm 0.52\times8+0.28\times6+0.2\times4=E\\\rm E= 4.16+1.68+0.8\\\rm E=6.64\)
The expected value of the number of letters in the selected person's home state will be 6.64.
Learn more about the expected values here:
https://brainly.com/question/3913865
solve the following inequality for z. write your answer in simplest form. -9-(2z-7)>-2z-6-5z
Answers
Answer:
z > -4/5
Step-by-step explanation:
-9 - (2z - 7) > -2z - 6 - 5z
Get rid of the parenthesis
*There is the number one in front of the parenthesis.-9 - 2z + 7 > -2z - 6 - 5z
Combine like terms:
-2 - 2z > -7z - 6
+2 > +2
Add 2 to both sides.
-2z > -7z - 4
+7z > +7z
Add 7 to both sides.
5z > -4
Divide both sides by 5 to get z.
z > -4/5
The sign stays the same unless you divide by a negative number---------------------------------
More on inequalities: https://brainly.com/question/21857626
Hope this helps! :)
What is the remainder when the following polynomial division is performed? Place the answer in the proper location of the gird. Do not include parentheses in your answer.

Answers
The remainder of the polynomial division \(\frac{\left(y^4-y^3+2y^2+y-1\right)}{\left(y^3+1\right)}\) is 2y²
How to determine the remainder of the polynomial divisionFrom the question, we have the following parameters that can be used in our computation:
\(\frac{\left(y^4-y^3+2y^2+y-1\right)}{\left(y^3+1\right)}\)
When the numerator is expanded, we have
\(\frac{\left(y^4-y^3+2y^2+y-1\right)}{\left(y^3+1\right)} = \frac{(y - 1)(y^3 + 1) + 2y^2}{y^3 + 1}\)
Split the expanded expression
\(\frac{\left(y^4-y^3+2y^2+y-1\right)}{\left(y^3+1\right)} = \frac{(y - 1)(y^3 + 1)}{y^3 + 1} + \frac{2y^2}{y^3 + 1}\)
Evaluate
\(\frac{\left(y^4-y^3+2y^2+y-1\right)}{\left(y^3+1\right)} = y - 1 + \frac{2y^2}{y^3 + 1}\)
From the above, we have
Quotient = y - 1
Remainder = 2y²
Hence, the remainder of the polynomial division is 2y²
Read more about polynomial division at
https://brainly.com/question/7693326
#SPJ1
HELPPPPPPP HELPPPPPPPPPPP HELPPPPPPPPPPP
(YOU SHALL GET BRAINKY IF U ANSWER)

Answers
Step-by-step explanation:
Compute the matrix of partial derivatives of the following functions.
(a) f(x, y) = (ex, sin(xy)) Drx, y) =
(b) f(x, y, z) = (x-y, y + z) Df(x, y, z) =
(c) f(x, y)-(xy, x - y, xy) Df(x, y) =
(d) rx, y, z) = (x + z, y-42, x-y) Df(x, y, z) =
Answers
For a vector-valued function
\(\mathbf f(\mathbf x)=\mathbf f(x_1,x_2,\ldots,x_n)=(f_1(x_1,x_2,\ldots,x_n),\ldots,f_m(x_1,x_2,\ldots,x_n))\)
the matrix of partial derivatives (a.k.a. the Jacobian) is the \(m\times n\) matrix in which the \((i,j)\)-th entry is the derivative of \(f_i\) with respect to \(x_j\):
\(D\mathbf f(\mathbf x)=\begin{bmatrix}\dfrac{\partial f_1}{\partial x_1}&\dfrac{\partial f_1}{\partial x_2}&\cdots&\dfrac{\partial f_1}{\partial x_n}\\\dfrac{\partial f_2}{\partial x_1}&\dfrac{\partial f_2}{\partial x_2}&\cdots&\dfrac{\partial f_2}{\partial x_n}\\\vdots&\vdots&\ddots&\vdots\\\dfrac{\partial f_m}{\partial x_1}&\dfrac{\partial f_m}{\partial x_2}&\cdots&\dfrac{\partial f_n}{\partial x_n}\end{bmatrix}\)
So we have
(a)
\(D f(x,y)=\begin{bmatrix}\dfrac{\partial(e^x)}{\partial x}&\dfrac{\partial(e^x)}{\partial y}\\\dfrac{\partial(\sin(xy))}{\partial x}&\dfrac{\partial(\sin(xy))}{\partial y}\end{bmatrix}=\begin{bmatrix}e^x&0\\y\cos(xy)&x\cos(xy)\end{bmatrix}\)
(b)
\(D f(x,y,z)=\begin{bmatrix}\dfrac{\partial(x-y)}{\partial x}&\dfrac{\partial(x-y)}{\partial y}&\dfrac{\partial(x-y)}{\partial z}\\\dfrac{\partial(y+z)}{\partial x}&\dfrac{\partial(y+z)}{\partial y}&\dfrac{\partial(y+z)}{\partial z}\end{bmatrix}=\begin{bmatrix}1&-1&0\\0&1&1\end{bmatrix}\)
(c)
\(Df(x,y)=\begin{bmatrix}y&x\\1&-1\\y&x\end{bmatrix}\)
(d)
\(Df(x,y,z)=\begin{bmatrix}1&0&1\\0&1&0\\1&-1&0\end{bmatrix}\)